以体验式教学助力学生数学思维提升
肖玉翠


本文以北师大版数学“图形的全等”一课为例,旨在探讨如何通过体验式教学活动的设计与实施,引导学生主动探究、发现全等图形的奥秘,进而在亲身实践中加深对全等图形概念、性质及判定方法的理解与应用,通过这一探索,期望为数学教学的创新与发展提供有益的借鉴与启示,共同推动学生数学思维能力的全面提升。
一、教材分析
“图形的全等”作为北师大版数学七年级下册的第四章第一节,其内容不仅局限于知识点的传授,还体现了数学知识之间的连贯性和逻辑性。在学生学习了基础的几何概念如线段、角、相交线和平行线以及三角形之后,本课程适时引入,旨在深化学生对图形间关系的理解。全等图形的探究不仅涉及概念和特征,还进一步延伸到对全等三角形的详细分析,包括其性质、对应关系和专用的符号表示。
二、学情分析
七年级学生已具备一定的几何基础,对线段、角等概念有了初步认识,但对全等图形的理解尚浅。他们好奇心强,喜欢动手操作,但抽象思维能力有待提升。因此,教师在教学中应注重直观演示和实践操作,帮助学生理解全等图形的本质特征。
三、教学目标
(一)知識与技能
1.深入理解全等图形的概念及其独特特征,能够准确阐述全等图形的定义。
2.熟练掌握全等图形的识别方法,能够在不同情境中准确区分全等图形。
3.对于给定的复杂图形,能够运用所学知识将其合理地分割为多个全等图形。
(二)数学思考、解决问题与情感态度
1.通过全等图形的认知、辨识及自主分割等学习活动,让学生深刻体验数学探索的乐趣和创造性,认识到数学学习的实用性和趣味性。
2.在师生互动的教学过程中,着力提升学生的图形分析能力,发展空间观念,并培养学生积极参与的精神和团队合作能力。
四、教学重难点
重点:深入理解全等三角形的概念及其基本性质,能够准确识别并标注全等三角形的对应边和对应角。
难点:灵活运用全等三角形的性质进行简单的几何推理和计算,解决实际问题。
五、教学过程
(一)创设情境,导入新课
(教师打开多媒体课件,展示一组剪纸图片,其中包括几对完全相同的图形)
教师:同学们,看看这些剪纸图片,你们发现了什么?
学生:哇,这些剪纸好漂亮!有几对图形看起来是完全一样的。
教师:没错,你们观察得很仔细。这些完全一样的图形,其实就是我们之前学过的——
学生:完全重合的图形!
教师:对,你们记得很清楚。完全重合的图形之间有一种特殊的关系,我们今天要学习的就是具有这种关系的图形——全等图形。
教师:同学们,你们知道什么是图形的全等吗?
学生:如果两个图形能够完全重合,那么这两个图形就是全等的。
教师:非常好,完全正确。两个全等的图形,它们的形状和大小都相同。
教师:那么,你们能举出一些常见的全等图形吗?
学生:大小相同的两个三角形、等腰梯形、正方形等。
教师:对,这些都是常见的全等图形。除此之外,还有一些特殊的全等图形,如通过平移、旋转后完全重合的两个图形也是全等的。
(教师点击鼠标,课件中相同的图形开始闪烁)
教师:现在,请大家再仔细观察一下,这些闪烁的图形有哪些特点?
学生(专注地看着屏幕):它们的形状和大小都一样!
教师:很好,你们总结得很到位。全等图形就是形状和大小完全相同的图形。那么,在我们的生活中,你们能想到哪些全等的例子呢?
学生(思考片刻):老师,我们用的作业本,每一本的封面都是一样的,它们应该是全等的。
教师:非常棒!你找到了一个很好的例子。全等图形在我们的生活中无处不在,只要我们用心观察,就能发现它们的身影。现在,让我们带着这些生活中的全等图形,一起进入今天的数学课堂,探索全等图形更多的奥秘吧!
(二)观察操作,探究新知
教师:好的,同学们,我们已经初步了解了全等图形的概念。接下来,我们将通过观察和操作进一步探究全等图形的性质。请大家看这里(教师展示一组全等三角形的剪纸),我手里有两个三角形剪纸,你们能发现它们之间有什么特别的关系吗?
学生A(仔细观察):它们的形状和大小都完全一样,所以它们是全等的。
教师:非常对,那么,如果我们把它们叠在一起,会有什么现象发生呢?
(教师将两个全等三角形剪纸叠在一起,学生观察)
学生B:它们完全重合了!
教师:没错。这就是全等图形的一个重要性质——完全重合。现在,请大家在自己的课桌上找两个全等的物品,试着叠在一起看看。
(学生开始寻找并操作)
学生:老师,我找了两块全等的三角板,它们叠在一起也完全重合了!
教师:很好,你们都通过自己的实践验证了全等图形的性质。那么,接下来我们要思考一个问题:如果我们有两个全等的三角形,它们的对应边和对应角有什么关系呢?
学生:对应边应该相等,对应角也应该相等。
教师:全等图形有哪些性质呢?
学生:全等图形的对应边相等,对应角相等。
教师:很好,全等图形的对应边和对应角都相等,这意味着它们的形状和大小完全相同。非常棒!你们通过观察和思考得出了正确的结论。全等三角形的对应边和对应角都是相等的,这个性质对我们解决几何问题非常重要。现在,请大家在小组内讨论一下,如何利用这个性质来解决一些实际问题。
(学生开始小组讨论,教师巡视指导)
教师:好了,同学们,看来大家都讨论得很热烈。现在,哪个小组愿意分享一下你们的讨论成果?
小组代表:我们小组认为,可以利用全等三角形的性质来证明两条线段相等或者两个角相等。如果两个三角形全等,那么它们的对应边就一定相等。
教师:非常好,小组的同学给出了一个很好的应用例子,通过观察和操作,我们不仅深入理解了全等图形的性质,还学会了如何应用这些性质来解决问题。希望大家在接下来的学习中能够继续保持这种探究精神。
(三)归纳总结,巩固练习
教师:如何判定两个三角形是否全等呢?
学生A:可以通过边边边(SSS)、边角边(SAS)、角边角(ASA)等方法来判断。
教师:对的,这些都是常用的判定三角形全等的方法。如果两个三角形的三组对应边或两对对应角分别相等,那么这两个三角形就是全等的。
教师:那么,如何证明两个图形是全等的呢?
学生B:根据判定全等的方法,我们需要找出两个图形的对应边和对应角,然后证明它们分别相等或满足特定的条件。
教师:对的,证明两个图形全等需要我们仔细分析图形的特征,找出它们的对应边和对应角,然后根据判定全等的方法进行证明。在这个过程中,我们需要严谨的逻辑推理和精确的计算。
教师:好的,同学们,我们已经通过观察和操作探究了全等三角形的性质,现在,让我们归纳总结一下今天的学习内容,并通过一些习题来巩固我们今天学习的知识。
学生C:老师,我知道全等三角形的定义是能够完全重合的两个三角形。
教师:非常好,那么,全等三角形的对应边和对应角有什么关系呢?
学生D:全等三角形的对应边相等,对应角也相等。
教师:非常对,这是全等三角形的重要性质,现在,请大家看这道习题(教师展示课件上的习题):
习题1:已知△ABC和△DEF是全等三角形,且AB=DE,BC=EF,∠A=∠D。请问:△ABC和△DEF的对应边和对应角分别是什么?
学生E(思考片刻):对应边是AB和DE,BC和EF,AC和DF;对应角是∠A和∠D,∠B和∠E,∠C和∠F。
教师:非常棒。你完全掌握了全等三角形的对应关系。那么,我们再来看一道稍微难一点的题目:
习题2:已知△ABC≌△MNO,且AB=MN,∠B =∠N。请问:如果BC=5cm,那么NO的长度是多少?
学生F:因为△ABC和△MNO是全等的,所以它们的对应边相等。已知BC=5 cm,那么NO的长度也是5 cm。
教师:非常好,你不仅理解了全等三角形的性质,还能准确地应用这些性质来解决问题。这就是我们今天学习的重点。希望大家在课后能够继续复习和巩固这些知识,为接下来的学习打下坚实的基础。
六、教学评价
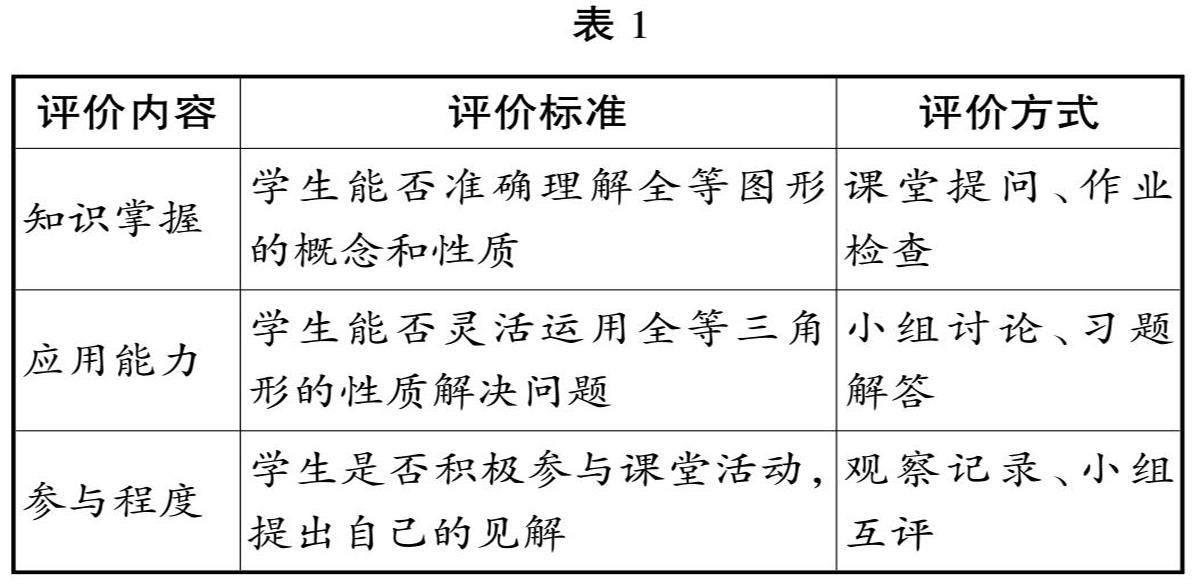
本节课通过创设情境、观察操作、归纳总结等教学环节,旨在引导学生深入理解全等图形的概念和性质,并能够靈活运用所学知识解决问题。在教学过程中,教师注重学生的实践体验,通过多媒体课件和剪纸等教具激发学生的学习兴趣,让学生在动手操作中探究新知。同时,教师还注重培养学生的观察能力和思维能力,引导学生通过观察和思考发现全等图形的性质和应用。整节课气氛活跃,学生参与度高,达到了预期的教学效果。(见表1)
七、教学反思
(一)以生活实例为切入点,增强学生体验感
为了让学生更加直观地理解全等图形的概念,我以生活中的实例为切入点,将抽象的数学概念与现实生活紧密相连,我引导学生寻找身边的其他全等图形,如书本的封面等,让他们在实践中不断加深对全等图形的认识。这种教学方式不仅极大地增强了学生的体验感,使数学知识变得更加鲜活和实用,而且有效地激发了学生的学习兴趣和探究欲望,为培养他们的数学思维能力奠定了坚实的基础。
(二)创设探究情境,引导学生主动发现
在教学过程中,我创设了多个探究情境,引导学生通过观察、操作和思考来发现全等图形的性质。在这一过程中,学生不仅亲自动手操作,还积极思考、主动发现,对全等图形的性质有了更深入的理解。
(三)注重实践应用,提升学生问题解决能力
为了让学生更好地理解全等图形的应用价值,我注重实践应用环节的设计。我引导学生利用全等三角形的性质解决一些实际问题,如测量距离、设计图案等。通过这些实践活动,学生不仅加深了对全等图形性质的理解,还提升了问题解决能力和数学应用能力。
(作者单位:甘肃省酒泉市瓜州县第三中学)
编辑:陈鲜艳

