离散型制造车间AGV小车自主避障路径选择研究

付 涛，景兴淇，李正雄，任 涛

（1.机械工业第六设计研究院有限公司，河南 郑州 450000；2.合肥工业大学，安徽 合肥 230009）

1 引言

离散型制造方式是通过单独生产分散零部件，并将零部件进行组装最终形成产品的一种生产方式[1]。飞机制造业、汽车制造业、服装加工业等机械加工类企业多为离散型制造企业。在生产流水线操作加工，组合多种零部件得到满足需求的汽车配件。离散型制造车间通常由仓储区、备料区、生产区、成品区等多个区域构成，采用AGV小车在各区域间运送工件能够极大地提升工作效率，减少人工成本，因此科学合理的AGV 小车路径规划选择以及选择自主避障策略在离散型制造车间生产过程中至关重要[2]。

文献[3]通过AGV 小车传感器探测周围环境障碍物，采用深度确定性策略梯度算法将AGV小车对环境的感知转化为动作输出，引入干扰学习结合深度确定性策略梯度预处理学习样本中的高斯噪声，提升算法鲁棒性，结合相关的计算结果实现AGV小车自主避障路径选择。文献[4]以AGV小车实时位置为基础构建动态障碍物矩阵，优化适应度函数后利用基于地图先验知识的粒子群优化算法求解障碍物矩阵，结合实时避障策略实现AGV小车自主避障路径选择。文献[5]通过改进蚁群算法的启发式信息和信息素更新策略提升算法寻优性能，对AGV小车避障任务进行优先级排序并优化冲突解决策略，避免多AGV小车路径冲突，实现AGV 小车自主避障路径选择。以上方法没有考虑动态环境中AGV小车运行相关的约束条件，导致AGV小车运行路径转折点较多、长度较长和规划用时较长的问题。

为了解决上述方法中存在的问题，提出离散型制造车间AGV小车自主避障路径选择方法。

2 离散型制造车间AGV小车多目标路径规划评价函数

2.1 建立多目标路径规划评价函数

所提方法采用栅格地图法建模离散型制造车间，将AGV小车运行空间划分为若干栅格[6]，综合考虑以下四个目标构建AGV小车路径规划评价函数。

2.1.1 路径长度目标函数

较短的运行路径能够提升AGV小车的工作效率并缩减运行成本等，用m表示AGV小车路径节点总数，xi、yi和xi+1、yi+1表示节点i和i+1的横纵坐标，d(i)，i+1 表示i与i+1之间的距离，路径长度目标函数f1如下所示：

2.1.2 转角和目标函数

对转角和加以控制能够提升AGV小车工作效率并减少因转弯造成的AGV小车车轮损耗等，因此将转角和作为AGV小车路径规划目标之一，用xi+2、yi+2表示节点i+2的横纵坐标，α(i，i+1，i+2)表示路径转角，构建转角和目标函数f2，如下所示：

2.1.3 危险率目标函数

AGV小车和障碍物之间距离与危险率呈负相关，用G(i)表示节点i危险率，c表示与i距离最近障碍物所处栅格中心，d(i，c)表示i与c之间距离，构建危险率目标函数f3，如下所示：

2.1.4 避障等待时间目标函数

当AGV小车遇到动态障碍物时需要原地等待直到障碍物离开，用z表示路径中避障总次数，t(k)表示第k次避障等待时间，构建避障等待时间目标函数f4，如下所示：

由此可得AGV小车多目标路径规划模型J=minF1，该模型含义为获取一条由起始点到终止点连续无碰撞且评价函数值最小的AGV小车运行路径。

2.2 确定权重系数

由于AGV小车在离散型制造车间中运输工件的各目标对评价函数的影响不完全一致，难以主观确定各目标对评价函数的影响程度，因此所提方法引入熵权法确定ω1、ω2、ω3和ω4取值［7］。假设spr表示标准化处理后第p个待评价路径的目标值r，计算该目标值的熵值h(r)，并以此为依据确定各目标权重系数ωr，如下所示：

3 AGV小车自主避障路径选择

3.1 动态环境下避障路径选择约束条件

当多个AGV小车共同出现于同一个环境中时环境发生动态变化，需要在静态规划的基础上对路径二次规划，因此基于感应技术提出适用于动态环境的感应转向方法，用于AGV小车在离散型制造车间中的自主避障路径选择。

在离散型制造车间中，各个AGV小车通常负责不同区域运输工作，不同情况下AGV小车避让方式，如图1所示。

图1 不同情况下AGV小车避让方式Fig.1 AGV Avoidance Under Different Conditions

3.1.1 AGV小车与固定障碍物相遇转向避让

由于离散型制造车间中可能存在栅格地图未及时更新、AGV小车运行路径中被临时放置货物、工作人员突然出现在运行路径中等情况，因此AGV小车在经过此处时需要执行感应转向方法实现自主避障，如图1所示。

为了避免因瞬时惯性造成AGV小车运输工件掉落或摩擦碰撞等情况，采用路径平滑度控制AGV小车转向，平滑度类似于曲率，与曲率呈负相关，加速度越小，AGV小车转向安全性越高，路径越短[8]。AGV小车处理器计算并选取生成的多条路径中曲率最小且与障碍物不发生碰撞的一条作为运行路径。将AGV小车运行轨迹以曲线形式呈现于坐标系并采用正交分解获取其轨迹方程以及相关约束条件，如下所示：

式中：ax、ay、bx、by、cx、cy、dx、dy—轨迹方程系数；x、y—横纵坐标上的点；x0、y0—AGV小车运行轨迹上的点。

约束（1）为AGV小车最小转角αmin约束，约束（2）为AGV小车最小轨迹曲率kmin约束，约束（3）是对AGV小车与障碍物最近距离R的约束，其中，'和＂表示一阶和二阶导数，和表示AGV小车与障碍物最近距离边缘上的点。用k表示曲率，构建平滑度目标函数f5，如下所示：

3.1.2 多AGV小车相向相遇转向避让

若存在多个AGV 小车相向相遇，例如AGVi和AGVj，如图1（c）所示。AGVi和AGVj互感后依据自身中心线和来车边缘距离计算获取转向方向，此时AGV小车的运行方式需要满足以下约束：

3.1.3 多AGV小车同向相遇转向避让

若多AGV 小车在同向行进过程中遇到未知障碍物，如图1（d）所示。为避免碰撞可采用跟随和超车两种避让策略，其中跟随在运行安全方面表现更为优异，因此优先选取减速跟随策略作为该情况下的避让方式，避免AGVi和AGVj发生碰撞，相关公式如下所示：

式中：L—AGV小车成功通过障碍物的总行进距离；v—运行速度；t—成功通过障碍物所用时长；Δs—两AGV小车相遇点到通过障碍物弧长；u、o—轨迹横坐标取值；f6—vmin加速度目标函数。

用ω5和ω6表示f5和f6函数对应权重系数，ω5+ω6=1，由此构建AGV小车自主避障路径选择函数F2如下所示：

同样采用熵权法计算权重系数ω5和ω6，选择使F2最小的路径作为动态环境下AGV小车自主避障路径。

3.2 AGV小车多目标路径选择

3.2.1 粒子群优化算法

在粒子群优化算法中每个粒子均与AGV小车的一条规划路径相对应[9]。依据粒子群更新规则得到第k+1次迭代中粒子i位置和速度如下所示：

式中：M—粒子群规模；D—可行解空间维度—第d维可行解空间第k次迭代中粒子i在栅格地图中的位置，d∈[1，D]，i∈[1，M]；—粒子速度；ϖ—动态惯性因子；—个体最优值；—全局最优值；c1、c2—不同的学习因子；r1、r2—［0，1］中随机数。

由于AGV 小车在多目标路径规划模型中变量和约束非单一，因此引入惩罚函数λ处理多变量约束问题，利用AGV小车运行时间构建适应度函数fitness，通过该函数衡量粒子寻优性能质量，则fitness如下所示：

式中：L(i，i+1)—粒子i和i+1之间的距离；w—粒子在其对应路径上的转弯次数；V—粒子群速度；T—完成一次转弯所用时间。

3.2.2 鸽群优化算法

为提升算法性能，引入鸽群优化算法与粒子群优化算法共同完成AGV小车多目标路径选择[10]。假设鸽群规模为N，依据鸽群优化算法更新规则得到第（t+1）次迭代中鸽子i位置和速度如下所示：

式中：—d维可行解空间第t次迭代中鸽子j所处位置；j∈[1，N]；—对应速度；R—地图罗盘算子；R∈[0，1]；r—［0，1］中随机数；gbest—全局最优值。

R值与搜索速度和开发能力呈负相关，采用线性变异策略动态选取R值，则R值确定方式如下所示：

式中：Pm—变异概率；Kmax—最大迭代次数；[Rmin，Rmax]—地图罗盘算子取值范围。

对地图罗盘算子的运算结束后开始地标算子运算，在地标算子运算过程中，每次迭代均舍弃种群中半数鸽子和远离目标的鸽子，更新后第（t+1）次迭代中鸽子中心位置和鸽子位置，如下所示：

fitness()—的适应度值；

Mt—第t次迭代中种群规模。

3.2.3 联合优化算法

将联合粒子群优化算法和鸽群优化算法共同用于AGV小车最优路径集合寻优，在粒子群优化算法中，粒子依据个体和全局最优值控制粒子飞行方向，若种群在局部最优值所在的小范围内持续搜索，会导致粒子陷入局部最优的问题，因此构建种群多样性评估函数实时检测种群多样性，以种群多样性是否达到阈值作为开启鸽群算法的标准，种群多样性评估函数gt，如下所示：

式中：M—种群规模；

L—可行解空间最大对角线距离；

—个体最优值；

Cd—d维度下粒子群中心。

采用联合优化算法获取AGV小车在离散型制造车间栅格地图中最优路径的主要流程，如图2所示。得到最优路径集合后，利用熵权法计算各目标权重系数ωq并通过式（5）获取评价值最低的路径作为AGV 小车最终运行路径，实现离散型制造车间AGV小车自主避障路径选择。

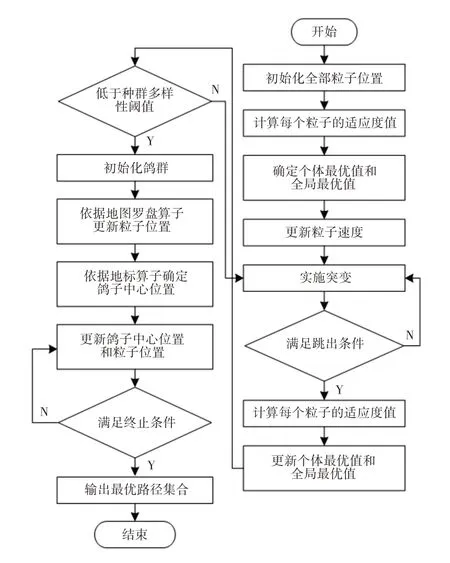
图2 联合优化算法获取最优路径集合流程图Fig.2 Flow Chart of Obtaining Optimal Path Set by Joint Optimization Algorithm

4 实验与结果

为了验证离散型制造车间AGV小车自主避障路径选择研究整体有效性，需要测试离散型制造车间AGV小车自主避障路径选择研究。实验用AGV小车，如图3所示。实验平台采用MATLAB2019a，实验操作系统运行内存为16GB，64位WIN10，实验以文献[3]方法和文献[4]方法为对照，每种方法中AGV小车运行参数均一致。建立栅格地图，所提方法、文献[3]方法和文献[4]方法中AGV小车起止位置和终止位置相同，分别对比三种算法在静态和动态环境中规划的AGV小车自主避障路径，如图4所示。

图3 实验用AGV小车Fig.3 AGV for Experiment

图4 静态环境AGV小车自主避障路径选择结果Fig.4 Selection Results of Autonomous Obstacle Avoidance Path for AGV in Static Environment

4.1 静态环境AGV小车自主避障路径选择结果

4.2 动态环境AGV小车自主避障路径选择结果

动态环境AGV小车自主避障路径选择结果，如图5所示。

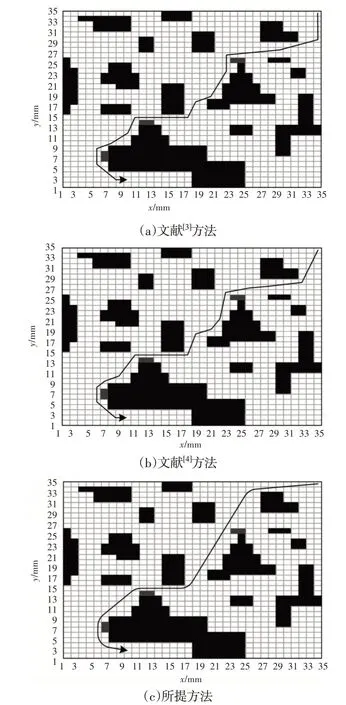
图5 动态环境AGV小车自主避障路径选择结果Fig.5 Selection Results of Autonomous Obstacle Avoidance Path of AGV in Dynamic Environment

由图4～图5可以看出，所提方法选择的避障路径中冗余路径和转折点更少，且所提方法选择的路径在经过障碍物时与障碍物之间保持一定距离，安全性更高，能够有效避免在遇到突发情况无法转向的问题，原因在于所提方法对在静态环境AGV小车自主避障路径选择中以转角和为目标函数之一规划路径，在动态环境中以平滑度为约束之一规划路径，从而减少路径转角，使路径平滑度更高。

为了客观评价三种方法的自主避障路径规划性能，统计三种方法在静态和动态环境中规划的AGV小车自主避障路径长度和路径规划用时，如表1所示。

表1 自主避障路径规划性能检测结果Tab.1 Performance Test Results of Autonomous Obstacle Avoidance Path Planning

由表1 可以看出，所提方法在静态和动态环境中规划的AGV 小车自主避障路径长度比文献[3-4]方法更短，同时路径规划用时也少于文献[3-4]方法，说明所提方法能够在更短的时间能作出更为优质的路径选择，更适合用于AGV 小车自主避障路径选择。

5 结束语

科学合理的AGV小车路径规划不仅能够提升离散型制造车间工件运输效率和订单完成效率，还能够使AGV小车运行更加平稳和安全，因此避障路径规划选择是AGV小车成功完成运输任务的基础和工作质量优劣的决定性因素。

为了解决目前存在的AGV小车运行路径转折点较多、长度较长和规划用时较长问题，提出离散型制造车间AGV小车自主避障路径选择方法。

将离散型制造车间作为栅格地图，构建各目标的目标函数并建立多目标路径规划评价函数，通过熵权法确定各目标权重系数，约束AGV小车运行过程中AGV小车的不同障碍避让情况，采用粒子群优化算法和鸽群优化算法联合寻优AGV小车运行路径集，得到最优运行路径，实现AGV小车平滑安全的自主避障路径选择。该方法能够有效地平滑AGV小车运行路径、缩短路径长度并减少路径规划用时，为AGV小车的应用奠定基础。