高导热环氧复合材料干式电抗器热点温升的仿真研究
曲展玉,钟昱尧,宋岩泽,2,谢子豪,孟雨琦,谢 庆,2
(1. 华北电力大学 电力工程系,河北 保定 071003;2. 华北电力大学 新能源电力系统国家重点实验室,北京 102206)
0 引 言
干式电抗器凭借线性度好、饱和性高、损耗小、运行维护方便等优点已成为在“双碳”战略下构建新型电力系统的重要发展方向[1]。然而由于其在户外长时间运行,电抗器包封材料会随着运行年限增加逐渐老化,导致电抗器的热点温升与耐热等级不匹配,致使绝缘击穿事故频发,成为电网持续可靠运行的安全隐患。
目前,国内外对干式电抗器温度的相关研究较多。工程上已有对电抗器绕组热点温升和平均温升的研究报道[2],如采用基于曲线拟合及热平衡原理的平均温升计算公式,便于研究电抗器在工程应用中的热性能[3]。相关学者采用有限元数值计算方法,开展了干式电抗器多物理场耦合研究[4-7]。李春[8]研制了一种以COMSOL 热点温升仿真计算为理论依据的干式电抗器温度在线监测系统。张宇娇等[9]对通风结构进行优化设计,解决了干式电抗器局部温升偏高的问题。FENG C 等[10]基于温度对导体区域导电性的影响,利用双向耦合分析法研究导电性与温升的相互作用关系。WU S Y 等[11]基于有限元算法对干式电抗器热点温度分布规律进行研究。针对干式电抗器包封材料的热应力效应,李小萍等[12]对比分析了不同固化促进剂对树脂凝胶时间及黏度的影响规律,提升了包封材料树脂固化物的力学性能。余传柏等[13]采用新型聚醚多元醇增韧环氧树脂,提升了环氧固化物的综合性能。赵春明等[14]研究了不同温度和通流环境条件对包封材料热膨胀系数的影响。
干式电抗器包封层数多,绝缘材料消耗大,目前考虑玻璃纤维-环氧复合材料导热性能对干式电抗器温度场影响的研究较匮乏,因此本文以干式电抗器包封材料为研究对象,建立复合材料热导率仿真计算模型,对常规和高导热环氧材料所构成的复合材料热导率进行计算。在此基础上,通过磁-电与流-热多物理场耦合仿真模型研究热导率对包封材料热点温度的影响,希望能为干式电抗器的绝缘优化设计、缩短研发周期提供参考。
1 仿真模型
1.1 几何结构
在COMSOL 多物理场仿真软件中构建干式电抗器的二维轴对称模型以及复合材料热导率仿真计算模型。
1.1.1 干式电抗器几何结构
以一台RKGKL-10kV-600A-20mH 型的干式电抗器作为研究对象,其包封材料高度为2.715 m,最大厚度为15.89 mm。该干式电抗器具有轴对称性,将模型简化为图1 所示的二维轴对称模型,其主要电气参数如表1所示。

表1 干式空心电抗器的主要电气参数Tab.1 Main electrical parameters of dry hollow reactor
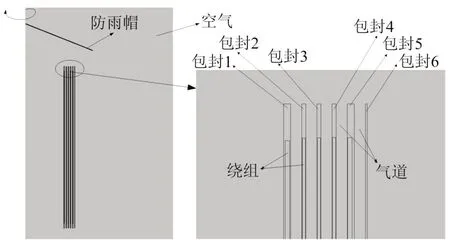
图1 干式空心电抗器系统仿真模型Fig. 1 System simulation model of dry hollow reactor
1.1.2 环氧复合材料几何结构
干式电抗器包封材料由浸有环氧树脂的玻璃纤维丝高温固化而成[15-16],玻璃纤维体积分数为65%,环氧树脂体积分数为35%。复合材料三维模型如图2所示。

图2 复合材料热导率仿真计算模型Fig.2 Simulation calculation model for thermal conductivity of composite material
1.2 数学模型
1.2.1 环氧复合材料热导率计算模型
材料的导热系数是指在稳定传热条件下,对于厚度为1 m、两侧表面积为1 m2且温差为1 ℃的材料,在1 s 内通过1 m2面积传递的热量,单位为W/(m·K)[17]。其傅里叶方程式如式(1)所示。
式(1)中:Q为热量,W;λ为热导率,W/(m·K);Α为材料截面积接触面积,m2;l为热量传递距离,m;T为温度,K;t为时间,s。
1.2.2 磁场-电路耦合
干式电抗器在结构上由多层绕组并联而成,在电路上等效为电压源与多层绕组并联的结构,各条支路等效为一个电阻Ri和电感Li(绕组编号i=1,2,...,n)的串联,各支路电感之间通过互感耦合。
采用有限元法分析干式电抗器的磁场-电路耦合问题,电压源等效为集中参数,并联线圈部分按照网格剖析进行离散化求解,分别得到耦合线圈的磁路部分和外部电压源的电路部分。磁场-电路耦合原理如图3所示。
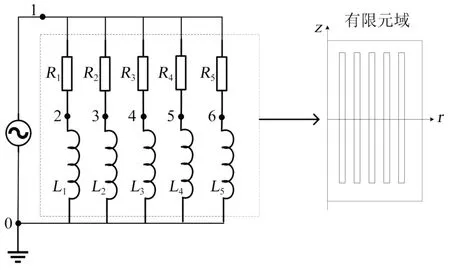
图3 磁场-电路耦合原理示意图Fig.3 Schematic diagram of magnetic field-circuit coupling principle
基于麦克斯韦方程组,线圈电磁场以磁矢势Α和电流Icir为自由度,干式电抗器的其他部分以磁矢势Α为自由度,满足磁场频域研究方程,如式(2)~(5)所示。
式(2)~(5)中:Η为磁场强度,A/m;Β为磁感应强度,T;Α为磁矢势,Wb/m;J为总电流密度,A/m2;Ε为电场强度,V/m;D为电通密度,C/m2;Je为线圈中的电流密度,A/m2;ω为角频率,rad/s;σ为电导率,V/m;j为虚数单位。
电抗器的外部电路方程为式(6)。
式(6)中:φ为电势,V;V为磁域体积,m3。
利用磁场计算得到的损耗作为热源,计算包封材料为常规环氧树脂复合材料的干式电抗器热点温升和温度场分布特点,进一步分析包封材料为高导热环氧树脂材料干式电抗器的热点温升。
1.2.3 流-热耦合
电抗器通过自然对流、热辐射和热传导3 种形式与外界空气进行热交换,电抗器内部能量以热能的形式传播,其内部固体和流体瞬态传热方程如式(7)所示。
式(7)中:ρ为密度,kg/m3;Cp为恒定应力下的比热容,J/(kg·K);T为绝对温度,K;utrans为平移运动的速度矢量,m/s;q为热通量矢量,W/m3;Q为额外的热源,W/m3;Qted为固体中的热弹性阻尼,W/m3。
2 仿真结果
2.1 常规/高导热环氧复合材料导热性能仿真研究
在环氧复合材料三维仿真模型中,设置不同热导率的环氧树脂材料,常规/高导热环氧复合材料各组分热导率如表2 所示,提取通过复合材料1 m2截面的稳态热通量,得到复合材料热导率与环氧树脂热导率的关系如图4所示。

表2 各组分热导率参数Tab.2 Thermal conductivity parameters of each component
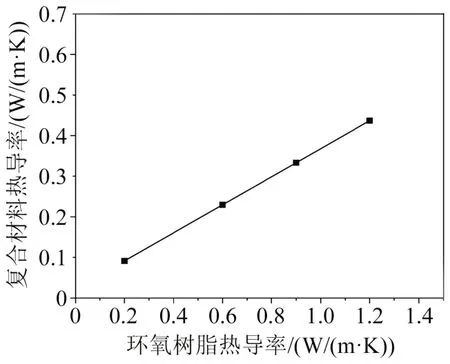
图4 包封复合材料热导率与环氧树脂热导率的关系Fig. 4 Relationship between thermal conductivity of encapsulating composite materials and epoxy resin
由图4可知,随着环氧树脂热导率的提升,复合材料的热导率呈线性增加,当环氧树脂热导率为1.2 W/(m·K)时,复合材料的热导率为0.44 W/(m·K)。
2.2 场路耦合结果
根据1.2.2中的磁场频域方程,仿真得到干式电抗器的磁通密度与磁矢势等值线分布如图5 所示,轴向和径向磁通密度模值分别如图6、图7所示。
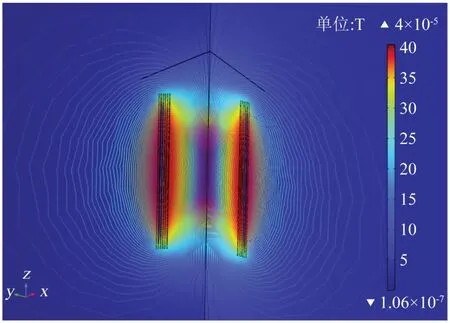
图5 正常情况下干式电抗器的磁场分布示意图Fig.5 Distribution diagram of dry-type reactor magnetic field under normal conditions

图6 径向磁通密度模值Fig. 6 Radial flux density modulus

图7 轴向磁通密度模值Fig.7 Axial flux density modulus
利用COMSOL的后处理功能,提取出干式电抗器在稳态和基频工况下各绕组的电流有效值和损耗值,此时第1~5层包封材料中的绕组体积依次为0.105、0.075、0.084、0.091、0.128 m3,仿真计算出各层电流有效值及体积热源密度,结果如表3所示。
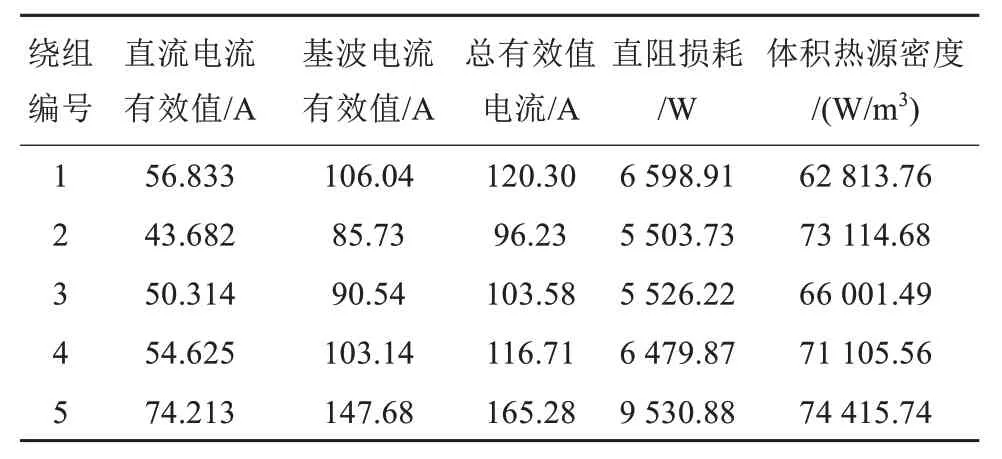
表3 磁场-电路耦合模型计算出的线圈电阻损耗Tab.3 Coil resistance loss calculated by magnetic field-circuit coupling model
由图6~7可知,径向方向上最内层包封材料的磁感应强度最大,轴向方向上高度中心位置处磁感应强度最大,因此磁通密度在最内层包封材料中心位置处取得最大值。由表3 可知,第5 绕组体积热源密度最大,这是由于最外层流过最大电流,因而产生最大的损耗。第1 绕组流过的电流大小与第4绕组接近,但由于第1绕组体积较大,因而体积热源密度较小。
2.3 常规环氧复合材料的干式电抗器温度场仿真研究
在COMSOL建立的二维轴对称模型中,将体积热源密度作为温度场模型的热源初始值,通过物理场剖分网格,设置合理的边界条件,按照表4设置材料各部分物性参数,计算模拟6 h 时的温度场分布云图。

表4 材料物性参数Tab.4 Physical property parameters of materials
图8为干式电抗器求解域内的温度场分布。从图8可以看出,随着高度增加,干式电抗器温度整体呈现上升趋势。图9 为干式电抗器的温度分布图。从图9可以看出,在25℃环境温度下,干式电抗器的最高热点温度为103.75℃,位于第4 层包封材料整体高度的约95.5%处,其温升为78.75℃。此外,第2~4层包封材料上端区域为热点集中区域。

图8 干式电抗器求解域内温度场分布Fig.8 The temperature field distribution in the solution domain of dry-type reactor
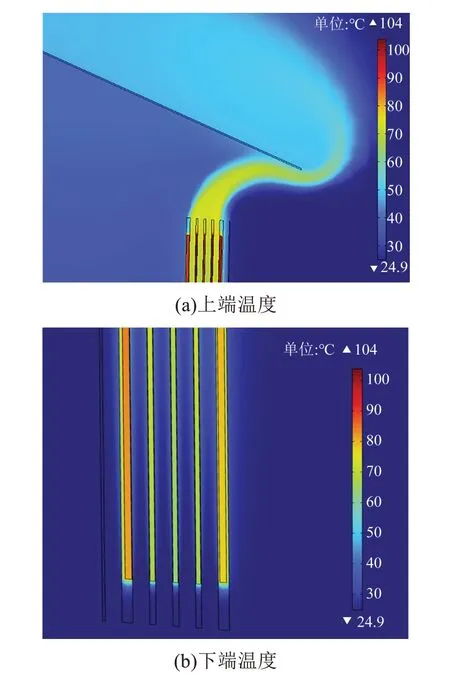
图9 干式电抗器的温度分布Fig.9 Temperature distribution of dry-type reactor
图10 为干式电抗器周围空气流场的流速分布。从图10 可以看出,求解域内空气的流速最大为1.95 m/s,位于防雨帽的上端檐。空气由下向上吸收包封材料的底部热量后,在自然对流作用下,空气的密度减小,进而加速流动上升,在进入风道时速度会较快。但由于空气在狭窄风道中对流效果变差,流速提升有限,因此在加速一定时间后空气流速保持稳定。当热空气进入上风道口后,已离开热源,速度开始减弱,一部分热空气沿着防雨帽边缘继续向上流动。
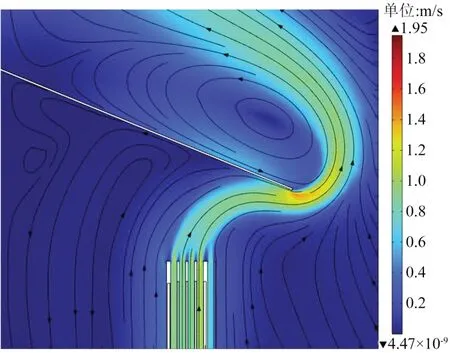
图10 干式电抗器周围空气流场分布Fig.10 The distribution of air flow field around the dry-type reactor
3 结果与讨论
3.1 包封材料的温度分布分析
为便于直观分析各包封材料的轴向温度变化情况,分别对6层包封材料取绕组中心截线,分析其温度变化情况,结果如图11 所示。从图11 可以看出,第1~5层包封材料的轴向温度分布趋势基本一致。在底部0~0.074 m 范围内,由于底部入口处空气流通较好,包封材料吸收大量热量,温度变化梯度最大。在0.074~2.641 m 高度范围内,包封材料内部热效应主要为热传导和热对流,空气对流效果稳定,此时电抗器温升变化不大。在轴向2.641~2.715 m高度范围内,风道与外界空气对流换热效果增强,温度明显下降。
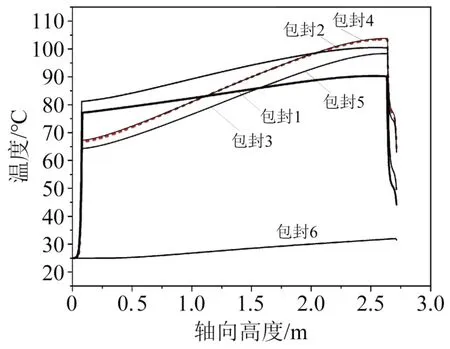
图11 干式电抗器的轴向温度分布规律Fig.11 Axial temperature distribution of dry-type reactor
对干式电抗器95.5%高度的径向截线数据集进行分析,温度变化曲线如图12 所示,曲线中波峰代表包封材料的温度,波谷代表气道口温度。
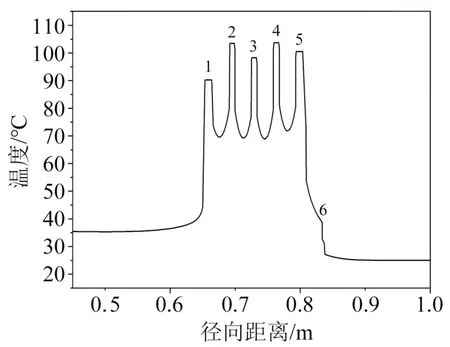
图12 95.5%高度位置处的径向温度分布规律Fig. 12 Radial temperature distribution pattern at 95.5% of height locations
由图12 可以看出,波峰与波谷之间的坡度较大,在电抗器各包封材料的同一高度上,位于第4层的温度最高,第2 层的温度次之,第1 层的温度最低。结合表3 中第2 层包封材料虽然流过的电流最小,但其绕组体积最小,所以其体积热源密度较大,仅次于第5 层包封材料,第4 层包封材料的体积热源密度稍小于第2 层包封材料。但由于第4 层包封材料位于电抗器中部,散热条件较差,而第2层靠近内侧通风区,所以第4层包封材料的热点温升最高。由于第6 层包封材料在最外侧阻挡了部分散热,因此第5层的热点温升也较高。最内层包封材料由于散热效果较好,温升较低。第6 层包封材料位于最外层,并且没有绕组产热,散热效果好,因此温度最低。
3.2 环氧复合材料热导率对干式电抗器热点温升的影响规律
由干式电抗器在正常状态下的稳态热点温升可知,其热点温升值为103.75℃,此时包封材料为常规环氧复合材料,其热导率为0.091 W/(m·K)。通过仿真计算常规/高导热环氧复合材料下干式电抗器的热点温升,结果如图13所示。结合图4和图13可以看出,环氧材料热导率为1.2 W/(m·K)时,复合材料的热导率为0.44 W/(m·K),高导热复合材料使电抗器从最高温103.75℃降到96.2℃,热点温升降低了7.55℃,降温效果显著。
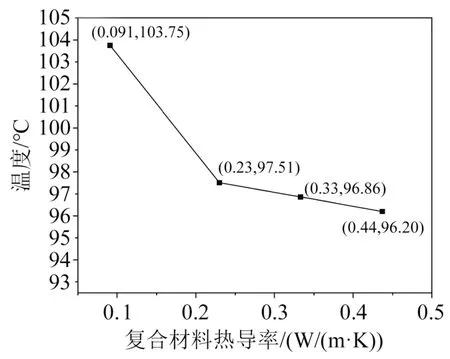
图13 不同环氧复合材料热导率对干式电抗器热点温升的影响Fig.13 Influence of thermal conductivity of different epoxy composite materials on the hot spot temperature rise of dry-type reactor
4 结 论
(1)利用COMSOL有限元仿真模型计算了不同复合材料的热导率,分析得到高导热环氧树脂对复合材料热导率的提升效果显著。
(2)包封材料本体及周围空气温度场区域中热点温升最大值为103.75℃,出现在内部第4 层包封材料的上端处;电抗器顶部和底部对流换热要优于中部,电抗器顶部温度变化能够表征整体温度状况。
(3)将仿真得到的常规和高导热环氧复合材料的热导率,作为材料特性输入热-流场仿真模型计算,发现高导热复合材料对降低干式电抗器热点温升的效果显著,使用热导率为1.2 W/(m·K)的环氧树脂,可以使干式电抗器热点温升降低7.55℃,证明了包封材料物性参数对干式电抗器温度场影响的重要性。

