低覆盖草地叶面积指数遥感估算方法
张云峰,任鸿瑞
(太原理工大学测绘科学与技术系, 山西 太原 030024)
草地是全球分布最广泛的植被类型之一,约占全球植被覆盖的42%,为社会的发展提供多种经济和生态效益[1]。草地生态系统是内蒙古的主要生态系统之一,植被种类和植物群落众多,不仅为野生动物提供了多种栖息地,还在有效保持水土、调节陆地碳循环和气候等方面发挥至关重要作用[2]。除此之外,草地也是发展畜牧业最基本的生产资料和基地。草地叶面积指数(leaf area index, LAI)定义为单位草地面积上植物总叶片面积的一半[3]。已有研究表明,LAI 与草地的生长过程息息相关,是衡量草地光合能力、初级生产力的一个重要指标[4-5]。根据刘纪远等[6]建立的土地利用/覆盖分类系统,将覆盖度在5%~20%的天然草地定义为低覆盖草地。由于植被信号在低覆盖区域较弱,光谱信号以土壤背景为主,叶面积指数估算受土壤背景影响较大,且估算精度较低。因此过去叶面积指数估算研究中,针对低覆盖草地的研究相对较少。对低覆盖草地LAI 进行精确估算,对监测低覆盖草地生长状况变化、研究草地质量变化及优化草地管理具有重要意义。
测量叶面积指数的方法通常包括直接测量法和间接测量法[7]。直接测量法通过采集样地中全部的叶片,利用方格纸计算采集到的叶片面积,进而计算样地的叶面积指数。虽然该方法具有较高的精度,但操作繁琐、费时费力,且会对地表植被造成一定破坏。间接测量可使用LAI 2000 等光学叶面积指数仪器,利用植被冠层间隙率来测定植被叶面积指数,该方法克服了效率及地表植被破坏等问题,但其测量精度却有待提高。上述2 种方法均只适合进行少量样地或小范围的叶面积指数测量,无法覆盖大范围。遥感技术的飞速发展使各类遥感数据层出不穷(如Landsat、Sentinel、Gaofen 等),遥感数据具有覆盖范围广、数据信息量大、数据获取周期短等特点,为大范围、高效率、高精度估算叶面积指数提供了帮助。叶面积指数的遥感估算方法可以分为物理模型法和统计模型法。物理模型法中最常用的为PROSAIL 模型,该模型为PROSPECT 模型与冠层植被SAIL 模型的耦合,具有较强的物理机理性,但该模型所需参数多,参数获取繁琐,且结果对设置的参数敏感性较强[8-10]。统计模型法利用各类统计方法寻求叶面积指数与波段反射率或植被指数间的关系,以此建立估算模型,该方法所需参数少,简洁清晰,易于使用,已常用于叶面积指数反演[11-12]。但研究发现,常用的统计模型法估算低覆盖草地叶面积指数表现不佳,存在高估现象[12]。机器学习模型相较于统计模型具有更强的数据挖掘能力,近年来已有研究者将其用于叶面积指数估算[13-15],利用机器学习的强大算法可提升叶面积指数的反演精度。沈贝贝等[16]利用随机森林模型对内蒙古草地叶面积指数进行估算时,由于其未考虑土壤背景影响,模型在低覆盖区域整体出现低估的现象。大多研究在使用机器学习模型进行估算时缺乏使用合理方法对特征变量进行优选,而这一步骤在提高模型效率和精度方面具有不可替代的作用。
由于一些研究区的自然环境较差,低覆盖草地在改良土壤、减少地面径流、防止水土流失等方面具有显著作用[17]。目前对叶面积指数估算的研究,通常将农作物、森林或中高覆盖草地作为研究对象,低覆盖草地叶面积指数估算还鲜有相关研究。本文利用Google Earth Engine 平台,以内蒙古草原草地低覆盖区作为研究区域,提取Landsat-8 遥感影像相关植被指数,结合实地测量数据将不同的特征优选方法(基于相关性和重要性)与不同机器学习模型(随机森林、梯度提升回归树)拟合,探究能有效估算低覆盖草地叶面积指数的方法,为制定有效地保护、管理草地策略提供依据。
1 材料与方法
1.1 研究区概况
内蒙古草原是中国四大草原之一,地域辽阔,地理范围(97°12′~126°04′ E,37°34′~53°24′ N),平均海拔约为1 000 m,面积86.68 万km2,草原面积占全国草原面积的1/3 以上。内蒙古草原地势平缓,南高北低;年内气温变化显著,年平均温度2~14 ℃,季节分明,全年无霜期110 d 左右;年内降水分布不均,集中分布在夏季,年降水量100~450 mm,自西向东递增,具有典型的半干湿的中温带季风气候特征。受气温、降水等多因素影响,内蒙古草原类型具有明显的地带性,荒漠草原、典型草原和草甸草原等多种地带性草原类型自西向东依次分布。图1展示了3 种草地类型在内蒙古草原的范围,数据来自唐家奎的中国内蒙古区域草地类型时空变异图[18]。
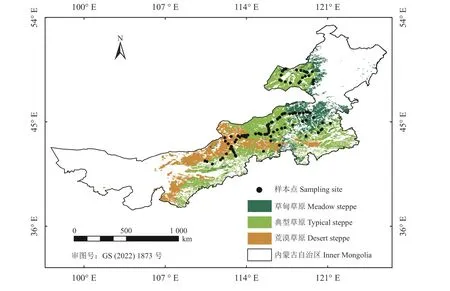
图1 内蒙古草原分布及草地叶面积指数采样点示意图Figure 1 Schematic diagram of steppe distribution and leaf area index sample sites in Inner Mongolia
1.2 数据来源与处理
1.2.1 实地数据收集
本研究地面实测LAI 采用直接测量法。实测地点为内蒙古草原,采样时间为2015 年8 月及2016年8 月,共选取99 个大样地,大样地范围足够大(样地边长大于90 m)以保证能与遥感数据分辨率更好地相匹配。大样地主要分布于内蒙古自治区中部地区,选择在植被空间分布较均匀且能代表大尺度区域的典型地段,与此同时考虑典型草原、荒漠草原、草甸草原3 种群落类型,及放牧、围封、自然3 种利用方式。在每个大样地中根据一致性、同质性、代表性原则设置3 个1 m × 1 m 小样方,采集小样方中全部植被,选取一组(20 株)具有代表性的植物,将其叶片放置于方格纸上(方格为1 cm × 1 cm),统计超出半格的格子数,作为该组植物的LAI。称量该组植物的干重,计算出比叶面积,再依据小样方中植被的总干重计算出小样方的LAI。取3 个小样方LAI 的平均值作为该大样地的LAI。在测量大样地LAI 同时,使用GPS 记录大样地的海拔及经纬度,以便后续研究匹配遥感影像。
1.2.2 Landsat-8 遥感数据
Landsat-8 卫星是美国航空航天局于2013 年成功发射的遥感卫星,其携带了陆地成像仪(operational land imager, OLI)和 热 红 外 传 感 器(thermal infrared sensor, TIRS)两颗传感器,重访周期为16 d。本研究使用了Landsat-8 卫星OLI 传感器提供的7 个多光谱波段,空间分辨率为30 m。
本研究利用GEE 平台对Landsat-8 数据进行预处理,并计算相关植被指数。由于实地测量数据采集时间为2015 年和2016 年的8 月,考虑影像时间覆盖不全以及部分点位对应影像有云覆盖,为最大限度兼顾所有样本点,故选取2015 年和2016 年7 月到9 月的影像,以均值合成的方式生成最终使用影像。
1.2.3 模型特征变量构建
本研究共选取22 个特征用于构建模型,包含6 个Landsat-8 影像的单波段反射率以及16 个常用植被指数(表1)。植被指数由不同波段反射率计算得到,相比于单波段,植被指数能更好地对植被特征进行表达,有效降低环境背景产生的影响,增加植被信息提取过程中的确定性[19]。

表1 模型特征变量Table 1 Vegetation index calculation formulae and sources
1.3 建模方法
1.3.1 机器学习模型
随机森林模型(random forest, RF)是当下研究最多、使用率最高的机器学习模型[4],其对样本数据集和特征集进行多次随机抽样,每一次抽样结果都将构建一棵有适合自身属性规则和判断值的决策树,最后由多棵决策树共同投票进行预测[35]。随机森林模型训练效率高,泛化能力强,能很好抵消噪声影响,且不容易出现过拟合现象。
梯度提升回归树模型(gradient boosting regression tree, GBRT)是一种基于Booting 算法的改进模型[36],它依次训练一组CART 回归树,对每一棵回归树的预测结果进行加和,并且每一棵回归树均对当前损失函数负梯度方向进行拟合,最终输出这一组回归树的加和作为回归结果。梯度提升回归树模型可解释性和鲁棒性好,有较强的回归预测能力。
1.3.2 特征优选方法
过多的特征变量会导致信息冗余,产生过拟合,降低模型效率,因此对用于构建模型的特征变量进行优选是建模过程中重要一环。梯度提升回归树模型和随机森林模型可以计算出每个输入模型的特征变量对模型的重要性,重要性值越大,说明该特征变量对模型估算LAI 越重要。将6 个单波段反射率和16 个植被指数(表1)分别按相关性、重要性从大到小排序,基于贪婪算法思想来寻求最佳特征个数,即依次选取排序前X 个特征(2 ≤ X ≤ 23)构建模型,以模型决定系数(R2)来确定最佳特征变量及个数。
本研究分别使用随机森林模型和梯度提升回归树模型结合两种特征优选方法进行建模回归分析,寻求适合估算低覆盖草地LAI 的模型。
1.4 精度评定
本研究将全部实测数据的80%用于训练模型,剩下20%用于评价模型泛化能力。训练模型采用五折交叉验证,将训练数据集尽可能均匀且不重复地分成5 份,其中4 份用作训练模型,1 份用于模型验证,不重复地进行5 次。用R2、均方根误差(root mean square error, RMSE)验证模型的精度。
R2可以表示模型预测值与实测值之间的拟合效果,R2越接近1,说明预测值与实测值越接近,模型回归拟合效果越好。RMSE 可以衡量实测值与预测值之间的偏差。当实测值与预测值完全吻合时,RMSE 为0,预测模型为完美模型;误差越大,该值越大。R2及RMSE 的计算公式分别为:

2 结果与分析
2.1 实测叶面积指数的统计分析
对2015 年和2016 年8 月草地实测数据进行统计分析(表2)。图2a 为不同类型草地叶面积实测数据的半箱型图,图2b 为不同范围LAI 值的实测点个数。总体上,LAI 在0.003~1.271,平均值为0.312,其中大部分样点的LAI 值为0.1~0.2,仅有4 个样本点的LAI 大于0.8。3 种草地类型中,实测值方差最大的为典型草原,方差最小的为荒漠草原;3 种草地类型的LAI 变异系数均较大,其中变异系数最大的数据在荒漠草原上采集得到,变异系数最小的为草甸草原上采集的数据。
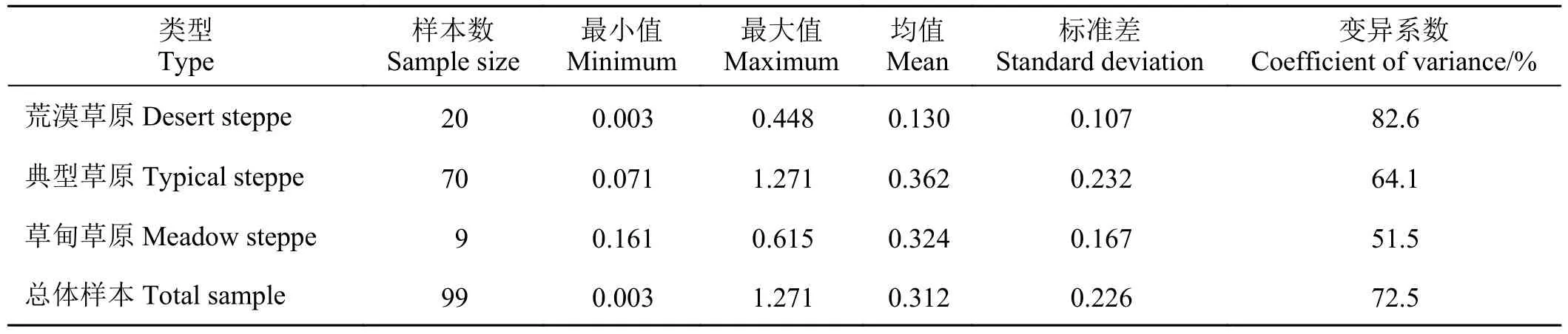
表2 2015 年和2016 年内蒙古低覆盖草地叶面积指数统计分析Table 2 Statistical analysis of low-cover grassland leaf area index in Inner Mongolia in 2015 and 2016
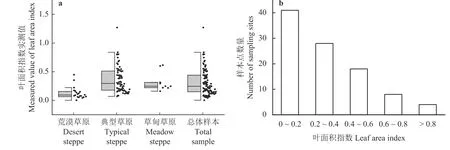
图2 2015 年和2016 年草原实测叶面积指数值统计图Figure 2 Statistical chart of measured leaf area index values in grasslands in 2015 and 2016
2.2 叶面积指数与各个特征变量之间的相关性
将从Landsat-8 影像中提取出的特征变量与对应实测点LAI 进行相关性分析(图3)。结果表明,在低植被覆盖的情况下,LAI 与单波段反射率及常见植被指数相关性均较差,相关系数均低于0.65;植被指数均与LAI 呈正相关关系,而单波段反射率则相反,均呈负相关关系;与LAI 相关性较大的特征变量均为植被指数,而单波段反射率相关性较低,其中,相关性最高的特征为GCC 和GLI,相关系数均为0.628;相关性最低的特征为SR-B5,相关系数仅为-0.30。综上结果表明,植被指数相较于单波段反射率具有与低覆盖情况下的草地LAI 更好的相关性。
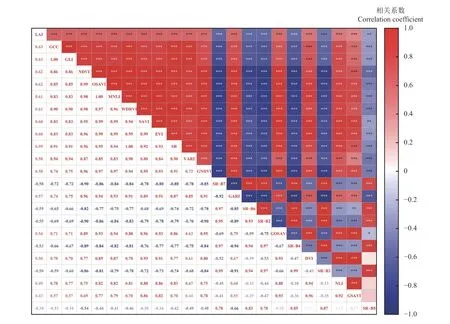
图3 各变量相关性热力图Figure 3 Correlation heat map of variables
2.3 机器学习模型构建
2.3.1 无特征优选随机森林模型和梯度提升树模型
将全部特征变量输入随机森林模型和梯度提升树模型,在无特征优选的情况下进行模型构建。结果表明,2 种模型尽管在训练集上取得较高精度(R2分别为0.618 和0.624,RMSE 分别为0.144 和0.142),但其在测试集上精度有待提高(R2分别为0.579 和0.550,RMSE 分别为0.117 和0.121)。
2.3.2 各特征变量在随机森林模型及梯度增强树模型中的重要性
基于上文构建的随机森林模型和梯度提升回归树模型,得出各特征变量在2 个模型中各自的重要性。22 种特征变量在随机森林模型和梯度增强树模型中的重要性百分比(图4)表明,输入的特征变量均对模型做出了贡献,其中重要性最高的特征变量为GLI,最低的为EVI。对比各特征变量的相关性排序(图3),部分特征变量不仅跟LAI 具有较高的相关性,在随机森林模型中也具有较高的重要性,如GLI;部分特征变量的排名发生了较大变化,如GARI、NDVI 和SR-B5。在梯度增强树模型中,重要性最高的特征变量为DVI,其余特征变量相较于DVI,重要性呈现断崖式下降;重要性值为0 的特征变量有3 个,分别为GLI、SR 和WDRVI,表明这4 个特征变量均未对构建梯度提升回归树模型做出贡献。相比相关性排序及随机森林模型重要性排序,多数特征变量的排名在梯度提升回归树模型中发生了很大的变化,如相关性较低的DVI,在梯度增强树模型中重要性最高;随机森林模型中重要性较高的GLI,在梯度增强树模型中却未做出贡献。

图4 特征变量在随机森林模型和梯度提升回归树模型中的重要性排序Figure 4 The importance sequence of feature variables in random forest and gradient boosting regression tree models
2.3.3 估算叶面积指数模型的构建与验证
特征优选过程中,随着输入模型特征数量的变化,模型的性能也会发生变化。基于2.2 及2.3.2 中对特征变量的排序进行特征优选,构建基于重要性、相关性特征优选的随机森林模型(I-RF 和r-RF)和基于重要性、相关性特征优选的梯度提升回归树模型(I-GBRT 和r-GBRT),确定各个模型所需特征变量后,使用交叉验证的方法对各个模型进行训练。图5为基于不同特征变量排序,不同数量的特征变量下,两类机器学习模型性能变化。两种随机森林模型(r-RF 和I-RF)分别选取20 个和4 个特征变量构建模型;两种梯度提升回归树模型(r-GBRT 和I-GBRT)分别选取5 个和8 个特征变量构建模型。表3 为各个模型最终选择的特征变量。

表3 不同模型所选择的特征变量Table 3 The selected feature variables of different models
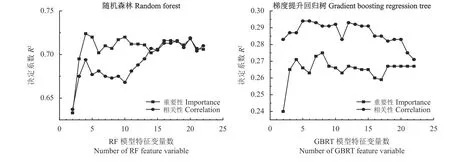
图5 不同数量特征变量下随机森林模型和梯度提升回归树模型的变化Figure 5 Variation of random forest and gradient boosting regression tree models with different numbers of feature variables
表4 为4 种模型应用在训练集和测试集上的结果,图6 为4 种模型在测试集上的预测值与LAI 实测值的散点图。总体而言,4 种模型在测试集上的R2相较于训练集均有所下降。随机森林模型中,效果最好的模型为r-RF 模型,其训练集R2为0.687,RMSE为0.130,测试集R2相较于训练集R2下降0.103,仅为0.584,RMSE为0.116;梯度提升回归树模型中效果最好的为r-GBRT 模型,训练集R2为0.702,测试集R2为0.686,散点图中各点相较于其他模型更加靠近拟合线,RMSE为4 个模型中最低,为0.101。I-RF 模型在训练集上效果不明显,训练集R2仅为0.643;I-GBRT 模型尽管在训练集上效果尚可,但其在测试集上效果不佳,R2仅为0.600,预测值与实测值相差较大,表明该模型泛化能力较低。对比特征优选前后模型结果显示,特征优选能有效提升机器学习模型性能;表4 结果也表明,基于相关性特征优选的模型在精度和泛化能力方面均优于重要性。

表4 4 种不同模型在训练集和测试集上的结果Table 4 The results of four different models in the training and testing datasets

图6 LAI 实测值和模型预测值的散点图Figure 6 Scatter plot of the measured values of the leaf area index and the values predicted by the model
3 讨论
由于在低覆盖区域,植被信号较弱,光谱信号以土壤背景为主,相关性结果中蓝光(Blue)、绿光(Green)、红光(Red)波段正常响应,但近红外(NIR)和短波红外(SWIR)波段与LAI 负相关,且NIR 与LAI 的相关系数较低。GCC 和GLI 未包含NIR 和SWIR 这两个波段的信息,故取得了较高的相关性。为降低土壤背景影响,本研究在确定构建模型的特征变量时,优先考虑了仅由蓝、绿、红波段组成的植被指数(VARI、GCC 等),还考虑了各类土壤调节植被指数(SAVI、OSAVI 等)。在I-RF 模型所筛选出的4 个特征变量中仅包含GLI,且选出了两个短波红外波段,导致模型精度相较于其他3 种模型有所降低。
本研究分别得出了各特征变量在两个机器学习模型中的重要性排序,相较于相关性排序,部分特征变量的位次发生了变化,这是因为相关性仅考虑各个特征变量与LAI 之间是否出现相关现象以及相关程度的大小,并未考虑特征变量之间的影响,而重要性则更加侧重表现各个特征在构建模型过程中的贡献程度的大小。由于特征变量的输入顺序对模型特征变量的重要性产生了影响,2 种机器学习模型的特征变量重要性排序之间也存在较大差异。随机森林模型综合评判了各个特征变量在随机森林每棵树上做出的贡献;而在梯度提升回归树模型中,各个特征变量的重要性受到第1 个输入模型的特征变量的影响较大,若后续特征变量与前面输入的特征变量具有相关性,则该特征变量的重要性将出现较大下降,这解释了在梯度增强树模型中,第1 个特征变量的重要性远大于后续特征变量的原因。因此在本研究中,为消除特征变量输入顺序带来的影响,两种模型计算重要性时,均将采用相同顺序输入各个特征变量。
本研究使用的r-GBRT 模型估算内蒙古低覆盖草地LAI 精度(R2= 0.686)相比于冷欣等估算[13]内蒙古草地LAI 精度(R2= 0.55)更高,提升约24.73%。
本研究中所使用的特征变量均是基于地面实测日期附近的遥感影像提取,但同时期影像有少部分缺失,无法完全覆盖,因此使用了少部分邻近日期的影像,这在一定程度上影响了模型精度;特征优选部分未来可寻找更优秀的特征筛选算法,进一步深入研究特征优选对模型精度的影响。
4 结论
以内蒙古草原中低覆盖草地为研究对象,使用光学影像数据提取相关植被指数作为特征变量,分析各个特征变量与草地LAI 的相关性及其在随机森林模型和梯度提升回归树模型中的重要性进行特征优选,基于优选特征变量构建随机森林回归模型和梯度提升树回归模型,并对模型精度进行验证。构建模型的特征变量中,GLI 和GCC 与低覆盖草地LAI 相关性较高;机器学习模型作为多变量模型在获取植被信息方面优于单变量模型(线性模型);借助先验知识选择特征变量能有效提升模型精度;基于相关性特征优选的梯度提升回归树模型(r-GBRT)相较于其他几种模型,使用特征变量少,估算精度最高,且泛化能力强;对比他人研究及相关LAI 产品,精度也有较大提升,说明该模型在估算低覆盖草地LAI 有一定应用价值。

