基于有限元法的中心牵引橡胶节点疲劳失效分析及改进研究

吴清坤 禚文 赵天

摘要：阐述某轨道车辆转向架用中心牵引橡胶节点结构特点及疲劳失效形式，通过有限元计算对失效位置进行复现，提出不同改进方案。利用有限元法对不同改进方案进行应力分析，选出最佳改进方案，并通过疲劳试验验证了产品的可靠性，可以为类似产品设计提供借鉴经验。

关键词：轨道车辆；中心牵引橡胶节点；有限元法；失效分析

0   引言

轨道车辆由于其运输量大、成本低、速度快等特点，在城市运输体系中占据举足轻重的地位[1]。随着车辆运行里程的增加，服役时间的延长，转向架承载部件质量问题也越来越多[2]。国内某轨道车辆转向架用中心牵引橡胶节点，在车辆运行50万km时出现批量橡胶开裂现象，裂纹均发生于产品下部，上部橡胶均未发生开裂。本文从橡胶开裂部位结合安装状态分析其失效形式及原因，借助有限元设计软件对应力情况进行分析研究，提出不同优化方案对比分析，并通过疲劳试验进行验证。

1   中心牵引橡胶节点结构特点及技术要求

1.1  结构特点

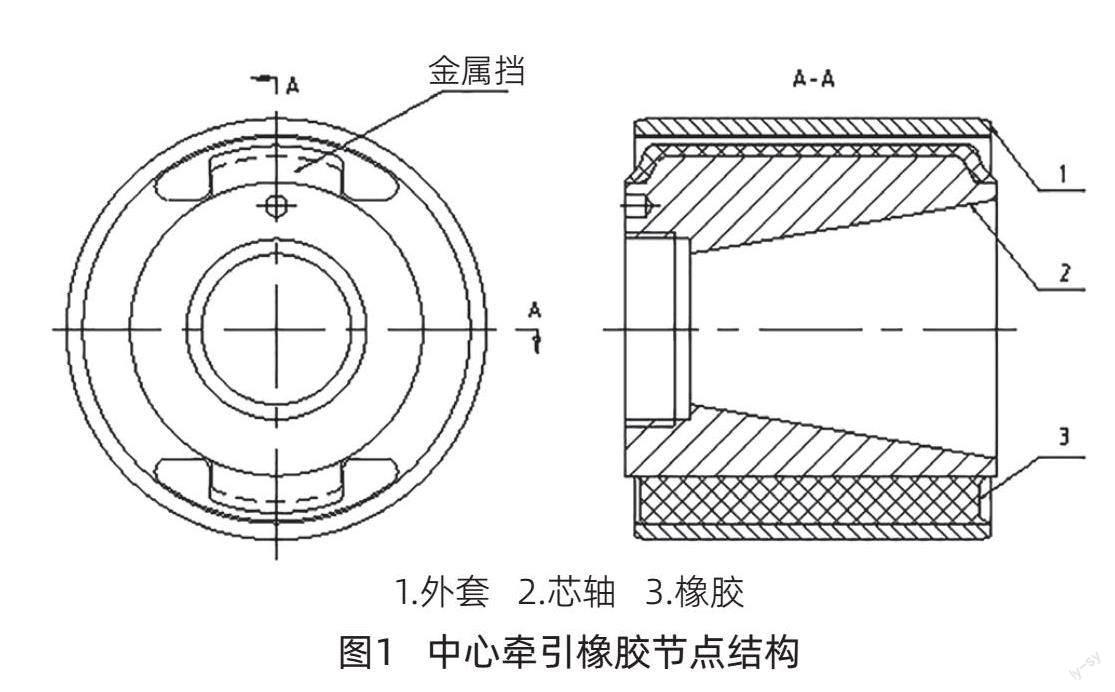
中心牵引橡胶节点由金属与橡胶硫化而成，具有多向刚度、降低金属磨耗、减轻质量、高频减振及隔音、良好的非线性等优点[3]，是转向架牵引装置的关键部件。它连接转向架与车体[4]，在车辆运行过程中，起到传递转向架和车体之间的纵向力及扭转力，以改善车辆振动噪声，提高乘客舒适度。中心牵引橡胶节点结构如图1所示。

为改善车辆动力学性能，提供不同横向、纵向刚度值，橡胶圆周方向采用不连续结构，即纵向橡胶开有缺口。同时，为限制纵向变形过大，芯轴设置金属挡凸起，外侧硫化一层橡胶，起到限位止挡且避免刚性冲击的作用。

1.2  技术要求

中心牵引橡胶节点主要技术指标为静态刚度性能及疲劳性能：静态刚度性能需满足表1要求。疲劳试验工况按照表2进行，疲劳性能需满足外观及静态刚度变化率要求，即疲劳试验后橡胶与金属粘接面开胶面积不应超过正常粘接面积的10%。金属不应出现裂纹或断裂，疲劳前后应满足静态刚度变化率公差限度值±20%以内[5]。

2   失效原因与解决方法分析

2.1  失效原因分析

中心牽引橡胶节点安装形式见图2，上部通过牵引销与车体连接，下部通过牵引拉杆组成与转向架连接，典型失效形式为下部橡胶缺口处开裂（图3），上部橡胶缺口处无开裂。

根据图2可知，中心牵引橡胶节点载荷实际作用线（牵引拉杆中心线）与理论作用线（中心牵引橡胶节点中心线）不重合，存在70mm左右偏心。当车辆运行时，其为传递转向架与车体之间载荷，中心牵引橡胶节点在实际作用线处承受偏心载荷，下部橡胶变形及载荷远大于上部橡胶，在交替疲劳载荷作用下，可能引起橡胶的疲劳失效。

为验证不同位置（理论作用线与实际作用线）加载对橡胶疲劳失效的影响，通过设计疲劳试验工装按照表2工况进行试验验证。试验结果表明：采用理论作用线加载方式进行200万次疲劳试验后，橡胶表面良好，无开裂现象；采用实际作用线加载方式仅进行120万次疲劳试验后，橡胶发生开裂现象，开裂位置与实际装车疲劳失效位置相同。因此可确认，橡胶失效是由于牵引装置实际作用线与理论作用线不重合造成的。

2.2   解决方法分析

解决中心牵引橡胶节点疲劳失效问题办法由2种：一是通过调整牵引装置加载位置，使其理论作用线与实际作用线重合；二是通过产品本身结构优化改善。产品偏心安装会降低使用寿命，若安装形式改为中心安装可降低批量失效风险，但目前该转向架已大批量装车运行，更改安装形式需耗费大量生产成本，并对线路正常运行造成影响，因此本文从产品本身考虑优化设计。

3   有限元分析

3.1   本构模型

橡胶属于高分子聚合物超弹性材料，具有各向同性和不可压缩的特点，其应力应变关系不能用简单线性描述，而是呈现复杂的非线性[6]。人们对橡胶本构模型进行的大量研究，一方面是基于统计热力学的理论，另一方面是基于连续介质唯象学理论[7]。两种理论发展出的应变能密度函数非常丰富，由于橡胶材料配方多样性能复杂，并非一种理论适用于所有情况，因此需针对具体问题具体分析，合理选择本构模型。

基于连续介质唯象学理论的Mooney-Rivlin模型是一个比较经典的模型，适用于应变约为100%（拉伸）和30%（压缩）的中小变形，应用广泛，对橡胶节点类结构产品仿真计算精度高，本文以该模型为理论基础进行有限元分析。

Mooney-Rivlin理论基于以下两个假设：一是橡胶材料具有体积不可压缩性，且在变形前是各向同性的；二是剪切变形中服从胡克定律，即应力-应变是线性关系。根据上述假设，通过数学论证推导出应变能函数W为：

W=C1（λ12+λ22+λ32-3）+C2（λ1-2+λ2-2+λ3-2-3）    （1）

式中：λ1、λ2、λ3为主拉伸比，C1、C2为常数。各向同性条件函数W对三个主伸长率λ1、λ2、λ3应为对称，因此应变能密度函数只是偶次幂函数，3个满足这些要求的最简单的偶数幂函数为：

I1=λ12+λ22+λ32                （2）

I2=λ12λ22+λ22λ32+λ12λ32             （3）

I3=λ12λ22λ32                 （4）

式种：I1、I2、I3为应变不变量。根据橡胶材料体积不可压缩性，三阶应变不变量I3为1，式（3）可写为：

I2=λ1-2+λ2-2+λ3-2               （5）

当I1、I2当作为独立变量时，式（1）应变能函数可表示为多项式型式：

（6）

其中Cij为常数可通过试验测的，典型的二项展开式为：

（7）

其中D1为常数，J为弹性体积比，由于橡胶几乎不可压缩性，J取值为1，式（7）可简化为：

W=C10（I1-3）+C01（I2-3）            （8）

式（8）中材料常数只有两个（C10和C01），可通过实测橡胶应力-应变和本构模型理论计算应力-应变通过最小二乘拟合得到。

3.2   失效应力分析

借助有限元仿真计算，以理论作用线为加载位置施加42kN纵向载荷，橡胶最大应力出现在橡胶中间位置，最大值1.029MPa（见图4）。以实际作用线为加载位置施加42kN纵向载荷，橡胶最大应力出现在橡胶端部位置，最大值2.338MPa（见图5）。最大应力值较理论作用线加载方式增加明显，最大应力位置也与实际装车疲劳失效位置相同，因此通过仿真计算可对疲劳失效形式进行有效模拟。

3.3   改进方案

中心牵引橡胶节点硫化时，温度变化会使橡胶内部产生初始拉伸应力。车辆运行过程中承受多种复杂載荷，也会使橡胶内部产生一定的拉伸应力。由于橡胶承受拉应力的能力较差，为改善产品应力状态，需对产品周向施以一定预压量，以消除橡胶内部拉伸应力，保证产品在工作时始终处在预压状态，从而提高产品寿命。

将中心牵引橡胶节点预压量分别设置为1mm（既有结构）、1.5mm、2mm、2.5mm、3mm，利用有限元分析进行偏心加载计算，通过调整橡胶硬度。在满足表1静态刚度性能前提下，计算纵向42kN载荷下橡胶最大应力，其计算结果如表3所示。由表3可知，预压量2mm时，各项刚度均满足技术要求，且最大应力值最小。

4   试验验证

根据有限元计算分析结果，牵引橡胶节点橡胶硬度选取58 Shore A，预压量2mm时橡胶应力最小，且刚度性能满足技术要求。为进一步验证有限元计算分析的可靠性，现对其进行试验验证。

对牵引橡胶节点静态刚度性能进行试验验证，试验结果见表4。从表4可知，试验结果符合技术要求。

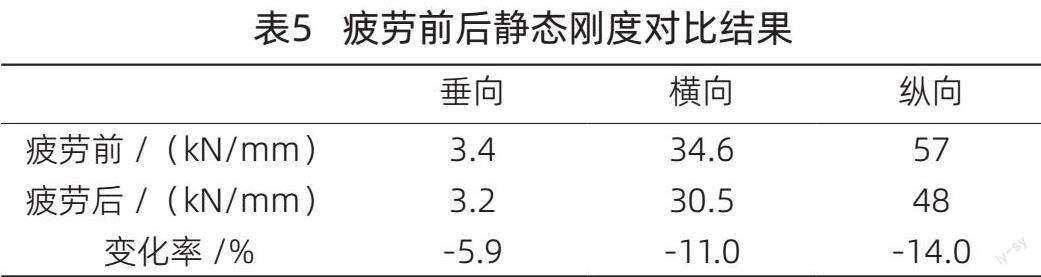
通过合理设计工装，模拟图2方式对中心牵引橡胶节点进行偏心加载（与理论作用线偏移70mm），按照表4进行200万次疲劳试验，疲劳试验后橡胶表面状态良好，无开裂现象，满足静态刚度变化率公差限度值（见表5）±20%以内。

5   结束语

中心牵引橡胶节点装车运行50万km后产生批量疲劳失效，是由于转向架牵引装置安装偏心，牵引拉杆中心线与中心牵引橡胶节点中心线不重合引起的。采用Mooney-Rivlin本构模型，对中心牵引橡胶节点刚度性能及应力情况进行有效分析，计算结果与试验结果吻合度较高。在不改变牵引装置结构前提下，通过调整中心牵引橡胶节点的预压量，可有效提高产品疲劳性能，满足装车要求。

参考文献

[1] 徐晓灵，王瑜琳，牟刚，等.轨道车辆转向架关键部件故障分析研究[J].科技风，2020（9）：120-121.

[2] 聂显鹏.转向架构架吊座裂纹原因分析及解决措施[J].山东工业技术，2020（5）：122-127.

[3] 严隽耄，付茂海.车辆工程[M].中国铁道出版社，2015：73.

[4] 马冬梅，周云峰，刘长江.城铁车辆转向架中心销套压装技术研究[J].机车车辆工艺，2022（1）：24-26.

[5] TB/T 2843-2015，机车车辆用橡胶弹性元件通用技术条件[S].国家铁路局，2015：8.

[6] 兰清群，邬平波.机车车辆用橡胶弹簧的静动态性能分析[J].机械设计与制造，2008（11）：43-45.

[7] 王刚.汽车动力总成橡胶悬置本构模型仿真分析及非线性动力学建模研究[D].西安：长安大学，2021（2）：13.