基于模糊测度的模糊分支时态逻辑模型检测*
刘子源,马占有,李 霞,高滢囡,何娜娜,黄瑞祺
(北方民族大学计算机科学与工程学院,宁夏 银川 750021)
1 引言
模型检测[1-3]是形式化验证的重要方法,其思想为用状态转换系统M表示系统模型的行为,使用逻辑公式F描述系统的性质,该系统能否满足此性质的模型检测问题转换为M是否满足逻辑公式F,若满足,通过验证;不满足,返回一个反例[4]。模型检测具有自动化验证的特点,并且以图论算法、数据结构和逻辑等理论作为基础[1],因此被广泛用于嵌入式系统、软件工程和硬件设计等领域。模型检测主要包括线性时序逻辑LTL(Liner Temporal Logic)模型检测和计算树逻辑CTL(Computation Tree Logic)模型检测等[5]。LTL和CTL的表达能力是无法比较的,在LTL中某些公式没有与之等价的CTL公式;同样在CTL中某些公式也不存在与之等价的LTL公式。分支时态逻辑CTL*(Computation Tree Logic*)包含了CTL和LTL两者的逻辑特性,可以表示CTL和LTL都无法表示的属性规约[2],因此,CTL*的表达能力比CTL和LTL更强。CTL*模型检测算法需要将LTL和CTL的检测算法进行适当组合[1,6]。
经典模型检测是一种定性的验证方法,对系统行为进行判定,结果只有正确和错误之分。定性模型检测无法表示和验证如“系统百分之九十的可能性不会死机”等属性规约。为解决上述问题,研究人员提出了定量模型检测,并受到广泛关注。定量模型检测主要包括概率模型检测、多值模型检测和模糊模型检测等。其中,Hart等[7]提出的概率模型检测用于解决模型检测算法中随机过程所造成的不确定性问题。Chechik等[8,9]提出的多值模型检测用于处理模型检测中含有不完全或不一致信息的问题。模糊模型检测解决了数据表述不确定性的系统模型检测问题[10]。
模糊模型检测是模糊集合理论与模型检测结合的模型检测方法。Li等[11-15]首先将模糊理论的分支可能性测度与模型检测进行结合,提出可能性模型检测和广义可能性模型检测,通过模糊博弈验证了模糊线性时序逻辑的可实现性。此外,范艳焕等[16]把不确定型模糊Kripke结构作为系统模型,对模糊计算树逻辑模型检测问题进行研究,给出了时间复杂度为对数多项式时间的改进算法。潘海玉等[17,18]把模糊Kripke结构作为系统模型,使用模糊计算树逻辑对不同模糊Kripke结构之间的关系进行研究,为模糊Kripke结构上的模糊计算树逻辑模型检测提供了新的方法。李召恺等[10]对模糊计算树逻辑模型检测问题进行研究,提出了模糊决策过程FDP (Fuzzy Decision Process)并将其作为系统模型,对模糊计算树逻辑模型检测问题进行研究,给出了基于模糊决策过程的模糊计算树逻辑模型检测算法。
本文将FDP模型作为系统模型,对模糊分支时态逻辑FCTL*(Fuzzy Computation Tree Logic*)模型检测问题进行研究,给出了FCTL*的语法和语义,本文参考文献[19]中的广义可能性测度理论,在模糊决策过程中引入模糊测度理论。然后给出FCTL*模型检测算法,该算法将FCTL*模型检测问题转化为模糊矩阵的合成运算,其具有高效、可读性强等优势。最后,对算法的复杂度进行了分析。
2 预备知识
本节介绍模糊集合概念和模糊矩阵运算等。
定义1[20,21]设X是经典集合,X上的模糊集合A是X到[0,1]的一个映射,也被称为模糊集合A的隶属度函数,A(x)表示x属于模糊集合A的隶属度,其中x∈X。
本文使用F(x)表示X上所有的模糊集合,即F(x)={A|A:X→[0,1]}。
定义2[20,21]设A,B∈F(x),任意x∈X,A与B的交、并、补的隶属度函数定义如下:
(A∩B)(x)=A(x)∧B(x)=min{A(x),B(x)}
(A∪B)(x)=A(x)∨B(x)=max{A(x),B(x)}
Ac(x)=1-A(x)
定义3[21]设X=(xuv)m× n,Y=(yuv)m× n均为m行n列模糊矩阵,X和Y的交、并、补定义如下:
X∩Y=(xuv∧yuv)m×n
X∪Y=(xuv∨yuv)m×n
Xc=(1-xuv)m×n
定义4[22]设X=(xuv)m×n是m行n列的模糊矩阵,Y=(yuv)n×l是n行l列的模糊矩阵,X和Y的内积定义如下:
X∘Y=(zuv)m×l
(u=1,…,m;v=1,…,l)
设P为模糊矩阵,其传递闭包[19]定义如下:
P+=P∨P2∨…∨P|S|
其中,S有穷且Pk+1=Pk∘P。
对于P,克林闭包P*定义为:P*=P0∨P+,其中P0为恒等矩阵。
3 模糊决策过程
本文采用文献[10]中提出的模糊决策过程作为模型,并在此基础上引入模糊测度。
定义5[10]FDP用于复杂模糊系统模型建模,是一个六元组Mf=(S,Act,P,I,AP,L):
(1)S为非空可数状态集;
(2)Act为动作集;
(3)P:S×Act×S→[0,1]为模糊转移函数,对于s∈S,α∈Act,有t∈S,使P(s,α,t)>0;
(4)I:S→[0,1]为初始分布函数,对于s∈S,I(s)表示初始状态是s的可能性真值;
(5)AP是原子命题集;
(6)L:S×AP→[0,1]为模糊标签函数,L(s,a)为命题a在状态s上的可能值,其中s∈S,a∈AP。
给定一个FDPMf,则称s0α0s1α1s2…∈π是从s0出发的无限路径当且仅当对于任意的i有P(si,αi,si+1)>0,其中π表示S上所有无限序列的集合。

定义6[10]设Mf=(S,Act,P,I,AP,L)为一有穷FDP,定义函数Adv:S→2Act是Mf的调度。对任意s∈S,有Adv(s)⊆Act(s)。
定义7设Mf=(S,Act,P,I,AP,L)为有穷FDP,Adv是Mf上定义的调度。定义映射FPoAdv:PathsAdv(Mf)→[0,1]如下:
其中,π=s0α0s1α1s2…∈PathsAdv(Mf)。
对E⊆PathsAdv(M),定义FPoAdv(E)=∨{FPoAdv(π)|π∈E}可以得到FPoAdv:2PathsAdv(Mf)→[0,1]是Ω=2PathsAdv(Mf)上的模糊测度[22]。
在有穷FDPMf=(S,Act,P,I,AP,L)上定义rAdv:S→[0,1],其中Adv表示调度,本文考虑最大调度rmax(s)和最小调度rmin(s),定义分别如下所示:
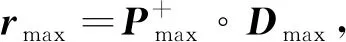

4 模糊分支时态逻辑
FCTL*是CTL*的扩展,FCTL*由状态公式和路径公式构成。下面给出FCTL*的语法及语义。
定义8(FCTL*语法) 原子命题集AP上FCTL*状态公式的正范式递归定义为:
Φ::=true|false|r|a|
其中,r∈[0,1],a∈AP,φ为FCTL*的路径公式。
FCTL*路径公式的正范式递归定义为:
φ::=true|false|r|a|
定义9(FCTL*状态公式语义) 设Mf=(S,Act,P,I,AP,L)是FDP,其中a∈AP,s∈S,Φ1、Φ2是FCTL*状态公式,φ是FCTL*路径公式,Adv为Mf上定义的调度,r∈[0,1],对于状态公式Φ,其在Mf上的语义是‖Φ‖:S→[0,1],归纳定义如下:对于任意的s∈S,
‖true‖(s)=1
(1)
‖false‖(s)=0
(2)
‖r‖(s)=r
(3)
‖a‖(s)=L(s,a)
(4)
‖a‖(s)=1-L(s,a)
(5)
‖Φ1∧Φ2‖(s)=‖Φ1‖(s)∧‖Φ2‖(s)
(6)

(7)


定义10(FCTL*路径公式语义) 设Mf=(S,Act,P,I,AP,L)是FDP,其中a∈AP,Adv是Mf上定义的调度,π=s0α0s1α1s2…∈PathsAdv(Mf),i≥0,s=s0,π[i]=si,πi=siαisi+1…,对于路径公式φ在Mf上语义是‖φ‖:PathsAdv(Mf)→[0,1],归纳定义如下:
‖true‖(π)=1
(8)
‖false‖(π)=0
(9)
‖r‖(π)=r
(10)
‖a‖(π)=‖a‖(π0)=L(s,a)
(11)
‖a‖(π)=‖a‖(π0)=1-L(s,a)
(12)
‖φ1∧φ2‖(π)=‖φ1‖(π)∧‖φ2‖(π)
(13)
‖○φ‖(π)=‖φ‖(π1)
(14)
‖φ1∪φ2‖(π)=
(15)
5 模糊分支时态逻辑模型检测算法
FCTL*模型检测问题是给定有穷FDPMf及FCTL*状态公式Φ,计算Mf中状态s满足Φ的可能性‖Φ‖(s)。FCTL*模型检测过程是由叶子节点向根节点遍历FCTL*状态公式Φ的语法树,其与FCTL模型检测算法原理相似。首先找到Φ状态极大真子式ψ[1],然后计算Mf中s满足ψ的可能性‖ψ‖(s),最后计算‖Φ‖(s)。
FCTL*模型检测过程中,用新原子命题集AP′={a1,a2,…}代替公式Φ中的状态极大真子式ψ[1]且新原子命题不会在公式Φ中出现。
对状态公式ψ=true,ψ=false,ψ=r,ψ=a,ψ=a,ψ=Φ1∧Φ2。‖ψ‖(s)由式(1)~式(6)可得。
当ψ=FPoAdv(φ)时,对一个FDP结构,只需要计算Mf中s满足FCTL*的正规范型公式FPo(φ)的可能性‖FPo(φ)‖的计算公式。
(1)φ=true。

‖true‖(π))=rmax(s)
(16)

‖true‖(π))=rmin(s)
(17)
(2)φ=false。

(18)
(3)φ=r。

(19)

(20)
(4)φ=a。

L(s,a))=L(s,a)∧rmax(s)
(21)

L(s,a))=L(s,a)∧rmin(s)
(22)
(5)φ=a。

‖
(1-L(s,a)))=(1-L(s,a))∧rmax(s)
(23)

‖
(1-L(s,a)))=(1-L(s,a))∧rmin(s)
(24)
(6)φ=φ1∧φ2。

‖φ2‖(π))=‖FPomax(φ1)‖(s)∧
‖FPomax(φ2)‖(s)
(25)

‖φ2‖(π))=‖FPomin(φ1)‖(s)∧
‖FPomin(φ2)‖(s)
(26)
(7)φ=○φ。


(Pmax∘‖FPomax(φ)‖)(s)
(27)

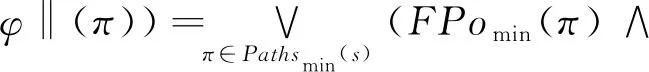
(Pmin∘‖FPomin(φ)‖)(s)
(28)
(8)φ=φ1∪φ2。

Pmax(sj-2,sj-1)∧FPomax(πj-1)∧
‖φ1‖(πj-1)∧Pmax(sj-1,sj)∧FPomax(πj)∧
‖FPomax(φ2)‖)(s)=
((Dφ1∘Pmax)*∘‖FPomax(φ2)‖)(s)
(29)
其中,Dφ1=(FPomax(φ1)(s))s∈S。

Pmin(sj-2,sj-1)∧FPomin(πj-1)∧
‖φ1‖(πj-1)∧Pmin(sj-1,sj)∧FPomin(πj)∧
‖FPomin(φ2)‖)(s)=
((Dφ1∘Pmin)*∘‖FPomin(φ2)‖)(s)
(30)
其中,Dφ1=(FPomin(φ1)(s))s∈S。
下面根据式(1)~式(30)给出基于FDP的FCTL*模型检测算法,为表达方便使用Adv表示最大可能性调度或最小可能性调度。算法中Sub(Φ)是Φ的子式的集合,|Φ|是Φ的极大真子式个数。

算法1 FCTL*模型检测算法输入:FDP Mf和FCTL*状态公式Φ。输出:对于Mf中任意状态s和调度Adv的‖Φ‖(s)。Procedure FCTL*Check(Mf,Φ)Step 1 for all i≤|Φ| doStep 2 for all ψ∈Sub(Φ) with |ψ|=i doStep 3 case ψ true:return(1)s∈S; false:return(0)s∈S; r:return(r)s∈S; a:return(L(s,a))s∈S; a:return(1-L(s,a))s∈S; Φ1∧Φ2 :return (FCTL*Check(Mf,Φ1)∧FCTL*Check(Mf,Φ2))s∈S; FPo(φ): case φ true:return(rAdv(s))s∈S; false:return(0)s∈S; r:return(r∧rAdv(s))s∈S; a:return(L(s,a)∧rAdv(s))s∈S; a:return((1-L(s,a))∧rAdv(s))s∈S; φ1∧φ2:return (FCTL*Check(Mf,FPoAdv(φ1)))s∈S∧ (FCTL*Check(Mf,FPoAdv(φ2)))s∈S; ○φ:return (PAdvFCTL*Check(Mf,FPoAdv(φ)))s∈S; φ1∪φ2:return (((FCTL*Check(Mf,FPoAdv(φ1)))PAdv)s∈S)*(FCTL*Check(Mf,FPoAdv(φ2)))s∈S Endcase;Endcase;Step 4 AP=AP∪{aψ};Step 5 replace ψ with aψ;Step 6 for all ‖ψ‖(s)>0 do L(s)={
本文给出的FCTL*模型检测算法是基于模糊矩阵运算的,下面对上述算法进行复杂度分析。在FCTL*模型检测算法中当ψ=ture,ψ=false,ψ=r,ψ=a,ψ=a,ψ=Φ1∧Φ2时,其复杂度与FDPMf大小和ψ的长度有关。当ψ=FPo(φ)时,且在φ=true,φ=false,φ=r,φ=a,φ=a,φ=φ1∧φ2时,复杂度同样与FDPMf大小和公式φ的长度有关;当φ=○φ时的复杂度与矩阵相乘有关,所以复杂度为多项式时间内的;φ=φ1∪φ2时的复杂度和克林闭包的计算有关,采用文献[23]的计算方式进行计算,可知复杂度为O(w2logw),w=|S|,其中|S|表示状态个数。
综上,本文提出的FCTL*模型检测算法的时间复杂度主要取决于算法中φ=φ1∪φ2的复杂度。给定一有穷FDPMf及FCTL*状态公式Φ,其模型检测算法的复杂度为O(size(Mf)·poly(S)·|Φ|),其中,size(Mf)表示模型的大小,poly(S)表示|S|的多项式函数,|Φ|表示FCTL*状态公式的长度。
6 实例说明
医疗专家系统是一种通过收集和分析大量医学数据协助医护人员进行诊断并给出治疗建议的计算机系统。本文采用文献[10,19]中的医疗专家治疗系统对FCTL*模型检测算法进行说明。图1是一医疗专家系统,其中有3位专家,每位专家给出不同的治疗方案,分别使用α,β,γ表示,图中圆圈表示该病人的身体状态,使用S0、S1、S2表示;状态中字母表示病人的身体状况:B(差),G(一般),F(好)。
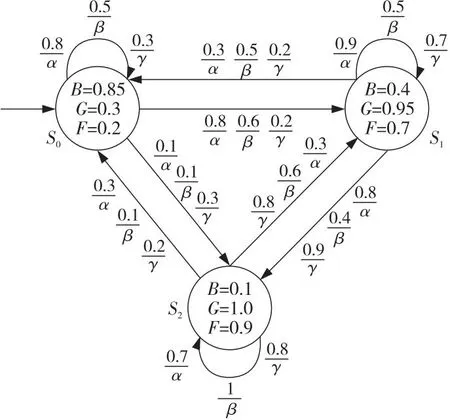
Figure 1 Medical expert system
多专家组成的专家系统较为复杂,但是可以避免某位专家全程治疗导致的主观性。本文使用FDPMf=(S,Act,P,I,AP,L)对病人的治疗过程进行建模,其中,S={S0,S1,S2},Act={α,β,γ},为了对病人的状态进行标记,设AP={B,G,F}。对于病人的3种身体状况,不同专家对此有不同的看法,因此,本文赋予一个模糊值来表示身体状况的健康程度。例如,L(S1,F)=0.7表示在状态S1上身体状况为“好”的程度是0.7;用P(S1,α,S2)=0.8表示医生采用α治疗方案对病人进行治疗后,病人的身体状态从状态S1到S2的可能性是0.8。
根据图1医疗专家系统模型,得出治疗方案α、β、γ对应的模糊转移矩阵Pα、Pβ、Pγ。B、G、F在状态S0、S1、S2对应的真值矩阵为PB、PG、PF。
专家结合3种方案对病人进行持续7天的治疗后,计算病人的身体状况最终为好(F)且一直保持好(F)的可能性,本文使用公式φ=◇≤7F∧◇□F描述这一性质[19]。下面根据FCTL*模型检测算法给出该公式的求解过程:
FPoAdv(◇≤7F∧◇□F)(s)=
FPoAdv(◇≤7F)(s)∧FPoAdv(◇□F)(s)=
当调度为最大调度时:
DF=diag(L(s,F)∧rmax(s))=
DF∘Pmax=
由此可得:
FPomax(◇≤7F∧◇□F)(s)=
同理可得当调度为最小调度时:
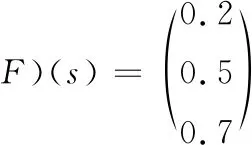
由上述计算可知,经过7天治疗后病人身体状况为好(F)且一直保持为好(F)的在状态S0、S1和S2处最大可能性分别为0.8,0.9和0.9;最小可能性分别为0.2,0.5和0.7。
计算病人身体初始状况为差(B),专家结合3种方案经过7天治疗后,病人的身体状况最终为好(F)并且最终一直保持身体状况为好(F)的可能性,本文使用公式Φ=B∧FPo(◇≤7F∧◇□F)来描述这一性质。根据FCTL*模型检测算法,下面给出该公式的最大可能性和最小可能性求解过程:Φ状态极大真子式为ψ1=B,ψ2=FPo(◇≤7F∧◇□F),对应的新原子命题集为AP′=AP∪{a1,a2}={B,G,F,a1,a2},公式ψ1=B的最大可能性及最小可能性根据FCTL*模型检测算法可得:
公式ψ2=FPo(◇≤7F∧◇□F)的最大可能性及最小可能性在前文已得到:


当调度为最大调度时:
L(S0)={0.85/B,0.3/G,0.2/F,0.85/a1,0.8/a2},
L(S1)={0.4/B,0.95/G,0.7/F,0.4/a1,0.9/a2},
L(s2)={0.1/B,1/G,0.9/F,0.1/a1,0.9/a2}
当调度为最小调度时:
L(S0)={0.85/B,0.3/G,0.2/F,0.85/a1,0.2/a2},
L(S1)={0.4/B,0.95/G,0.7/F,0.4/a1,0.5/a2},
L(S2)={0.1/B,1/G,0.9/F,0.1/a1,0.7/a2}
综上可得:
‖Φ‖max(s)=‖ψ1∧ψ2‖max(s)=
‖ψ1‖max(s)∧‖ψ2‖max(s)=
‖Φ‖min(s)=‖ψ1∧ψ2‖min(s)=
‖ψ1‖min(s)∧‖ψ2‖min(s)=
由上述计算可知,当病人身体状况为差(B)时,专家结合3种方案经过7天治疗后,病人身体状况变好(F)且一直保持好(F)在状态S0、S1和S2处最大可能性分别为0.8,0.4和0.1,最小可能性分别为0.2,0.4和0.1。
7 结束语
针对FCTL*模型检测问题,本文在FDP的基础上结合模糊测度理论给出了FCTL*的语法和语义;设计了FCTL*的模型检测算法,该算法将模型检测问题转化成模糊矩阵的合成运算,并进行复杂度分析;最后通过医疗专家系统的实例对算法进行了说明。

