基于改进型3D_Henon混沌映射的彩色图像加密方法*
牛士铭,薛 茹,丁 聪
(西藏民族大学信息工程学院,陕西 咸阳 712000)
1 引言
随着网络技术的普及和应用,图像成为了人们交流信息的重要方式。然而,由于网络是开放并且互相连接的,不法分子很容易监听、拦截、篡改或重新发布网络中传输的信息,图像信息在网络传输过程中的安全性令人担忧。因此,图像数据先进行加密处理后再传送是十分必要的[1,2]。
图像的扩散是指将图像的像素值通过某种方式进行改变,使图像丧失原有的特性。其中,混沌加密是扩散思想在图像加密中的主流应用[3-12]。常用的图像加密混沌映射方法有Logistic混沌映射方法[3-6]、Henon混沌映射方法[7,8]和Lorenz混沌映射方法[9]等。但是,已有研究表明,一维混沌映射的轨道可以很容易预测;而二维混沌映射[7,8]的混沌空间小,复杂度也较低;高维混沌[9]不仅复杂度极高,而且其计算的能量消耗也非常大。因此,以最少的状态变量和最高的系统复杂度来构建出结构紧凑和功能强大的非线性混沌系统,无疑具备十分重大的现实价值和科学意义。
为了提高现有混沌映射模型的混沌空间及混沌能力,构建出结构紧凑和功能强大的混沌映射模型,本文在归纳总结经典的Henon混沌映射原理和Sine混沌映射理论的相关研究基础上,对现有混沌系统函数表达式模型和经典混沌系统参数模型等进行了综合优化改进,设计了一个改进的3D_Henon混沌映射模型。通过对混沌空间分叉图、混沌空间轨道和Lyapunov指数等进行分析讨论和模拟计算后可知,相比经典的Henon模型和Sine模型,3D_Henon混沌映射模型具有更大的混沌映射空间、更好的混沌空间遍历性和更高的系统复杂度。
对于密码系统来说,如果使用重复的密钥,则密钥容易遭受暴力破解,从而造成系统安全问题。针对此问题,本文结合Chebyshev映射和明文,设计了一种密钥生成方法。
目前大多数加密算法都将像素视为图像中最小的元素(原子),即在像素级实现排列和扩散[10-17]。事实上,位级的排列不仅改变了像素的位置,还改变了它的值,对位平面进行操作会有更大的可操作空间和安全性[18-22]。王瑶等[21]利用一维 Logistic 自嵌入混沌系统,结合置乱和扩散操作,提出一种混沌图像加密算法。此算法先使用Zigzag算法对图像位平面进行置乱,之后像素级图像置乱一次,最后在扩散阶段,采用逐行策略进行扩散。
本文结合改进型3D_Henon混沌映射模型、新的密钥生成方法以及位平面加密的思想,设计了一种彩色图像加密方法。首先,要加密的彩色图像按照RGB颜色通道进行分离,形成3个二维矩阵。然后,将每个二维矩阵分别利用位平面分解技术分为8个位平面,使用3D_Henon混沌映射从Fibonacci置乱方法、Arnold置乱方法和Zigzag置乱方法中随机选择3次,分别对R、G、B平面所分解的位平面进行置乱,置乱结束后利用位平面合并技术对置乱后的位平面进行合并。然后,利用本文设计的密钥生成器产生3个15位的小数,作为后面混沌映射的初始值,并将此初始值作为图像加密方法的密钥。最后,置乱后的3个通道矩阵通过改进型3D_Henon模型进行扩散,完成加密操作。模拟实验结果表明,该方法具有优秀的图像加密效果,对常见的攻击具有较强的抵抗力,且易于实现。
2 改进的3D_Henon混沌映射模型
经典Henon混沌映射是一个由2个变量X和Y同时确定的二维迭代方程,其系统方程如式(1)所示:
(1)
其中,X和Y是系统的控制变量,a和b表示系统控制参数。研究结果表明:当函数a=1.4,b=0.3时,函数即进入了混沌状态,生成函数的混沌序列有很强的随机性。令X和Y的初始值为(0.1,0.2),其分叉图像如图1a和图1b所示,其相位图如图2a所示。
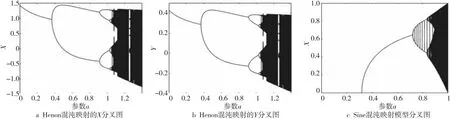
Figure 1 Bifurcation diagrams of Henon chaos mapping and Sine chaos mapping

Figure 2 Comparison of chaotic locus of Henon chaos mapping and 3D_Henon chaos mapping
Sine混沌映射为单峰映射,其定义如式(2)所示:
Xi+1=asin(πXi),a∈[0,1],Xi∈(0,1)
(2)
其中,Xi是第i次迭代的序列值,i取非负整数,Xi∈(0,1);a是系统参数,当a∈(0.87,0.93)和a∈(0.95,1)时出现混沌现象,令初始值X0=0.1,其分叉图如图1c所示。
本文的三维混沌映射表达式是在经典Henon混沌映射表达式和Sine混沌映射表达式的基础上再通过对函数表达式和系统参数表达式进行一定的改进得出的。改进型3D_Henon混沌映射函数的表达式如式(3)所示:
(3)
其中,a和b是混沌系统的控制参数,X和Y是系统的控制变量。令b=0.87且a∈(0,15],图3给出的是改进型3D_Henon混沌映射的分叉图。对比图1和图3可以看出,改进型3D_Henon混沌映射相对于经典Henon混沌映射来说其混沌空间更大,且混沌的输出遍历性也更好。令b=0.87,a=12.56,得到3D_Henon混沌映射的混沌轨迹,如图2b所示。
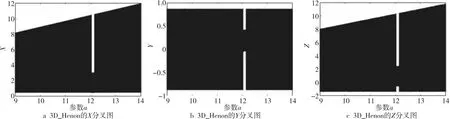
Figure 3 Bifurcation diagrams of 3D_Henon chaos mapping model
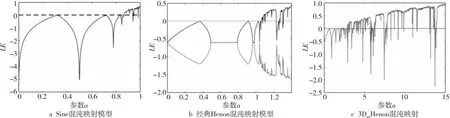
Figure 4 Comparison of Lyapunov exponent of Sine chaos mapping model,classical Henon chaos mapping model and improved 3D_Henon chaos mapping model
Lyapunov指数可被视作衡量复杂的混合系统的动力学行为的一个重要指标[23]。三维混沌系统有3个Lyapunov指数,只要1个Lyapunov指数大于零,便能证明该体系处于混沌阶段,而当有2个或者更多的Lyapunov指数大于零时,该混沌系统即为超混沌系统。如图4a~图4c分别为Sine混沌映射、经典Henon混沌映射和改进型3D_Henon混沌映射的Lyapunov指数动态图,其中,横坐标为参数a的取值范围,纵坐标为LE(Lyapunov指数)。当a=1时,Sine混沌映射的最大Lyapunov 指数为0.71。当b=0.3,a=1.4时,经典Henon混沌映射的最大Lyapunov 指数为0.44。当b=0.87,a=15时,改进型3D_Henon混沌映射的最大Lyapunov指数为0.98。因此,3D_Henon混沌映射相比传统Henon混沌映射有更大的混沌空间且混沌现象也更突出。且从图4中也可以看出,3D_Henon混沌映射的3个Lyapunov指数均大于0,说明3D_Henon混沌映射为超混沌映射。
近似熵(appEn)是一种重要的非线性动力学参数[24],它可以帮助研究人员更好地理解时间序列的复杂性,从而更好地预测其变化趋势,同时也可以帮助研究人员更好地探索时间序列中未知的变化,从而更好地掌握时间序列变化规律。时间序列越复杂,其近似熵也会越大。令a∈[0.8,1],经典Sine混沌映射模型的近似熵动态图如图5a所示。令b=0.3,a∈[0.8,1.5],经典Henon混沌映射模型的近似熵动态图如图5b所示。令b=0.87,a∈[0,15],3D_Henon混沌映射模型的近似熵动态图如图5c所示。由图5可以看出,与Sine混沌映射模型和经典Henon混沌映射模型相比,3D_Henon混沌映射模型拥有更大的近似熵,说明3D_Henon混沌映射拥有更加复杂的时间序列。
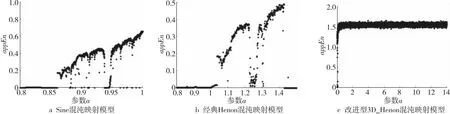
Figure 5 Comparison of approximate entropy graphs of Sine chaos mapping model,Henon chaos mapping model and improved 3D_Henon chaos mapping model

Figure 6 Bifurcation diagram of Chebyshev map
3 新的密钥生成方法
Chebyshev映射公式如式(4)所示:
Xn+1=cos(karccosXn),Xn∈[-1,1]
(4)
其中,k为Chebyshev 的映射阶数。当k≥ 2时,系统处于混沌状态。Chebyshev映射分叉图如图6所示。
本文利用经典Henon混沌映射随机生成100个整数。提取明文图像的100个整数所代表的位置信息上的像素值,设提取出来的前50个像素值的平均值为x0,后50个像素值的平均值+2为k。分别取x0和k作为Chebyshev映射模型的初始值和映射阶数,使用Chebyshev 模型随机生成5 000个15位的小数。从5 000个数字中随机选择3个值作为3D_Henon混沌映射的3个初始值,此初始值也是整个加密方法的密钥。此密钥生成方法可以每执行一次密码系统就自动生成一个新密钥。密钥生成方法如图7所示。
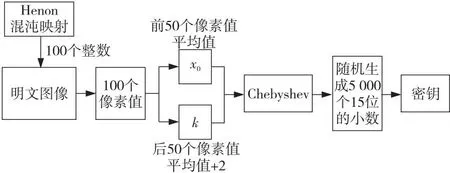
Figure 7 Key generation method
4 加密方法的设计与实现
本文的加密方法分为5个部分。第1部分是图像分解,包括彩色图像分通道以及通道平面进行位平面分解。第2部分是生成密钥,使用Logistic映射生成置乱算法的密钥;在原始图像中随机选出2个元素作为Chebyshev的初始值,使用密钥生成方法生成3个随机的15位小数,作为扩散函数的初始值,这也是加密方法的密钥。第3部分是图像置乱,通过改进型3D_Henon混沌映射模型从Fibonacci变换、Arnold 变换和Zigzag变换中分别选择一种置乱算法对 R、G、B 通道所分解的位平面进行置乱。第4部分是图像扩散,置乱后的3个通道平面通过改进型3D_Henon混沌映射模型进行扩散。第5部分是图像合并,包括位平面合并和将3个通道平面合并为密文图像。具体的加密过程如图8所示。
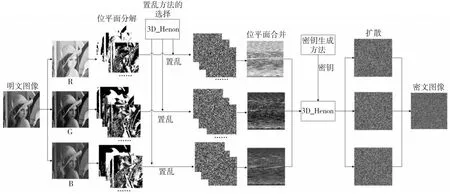
Figure 8 Process of image encryption
对于给定的彩色图像image,加密的详细过程如下所示:
(1) 对彩色图像分通道。
将彩色图像image按照RGB通道分离出R平面、G平面和B平面。
(2) 对位平面进行分解。
分别对R平面、G平面和B平面进行位平面分解,分解后分别得到8幅位平面图像。
(3) 选择所使用的置乱方法进行置乱操作。
使用3D_Henon混沌映射从Fibonacci置乱方法、Arnold置乱方法和Zigzag置乱方法中随机选择3次,分别对R、G、B平面所分解的位平面进行置乱。选择方法如下:使用3D_Henon混沌映射随机生成一个数,取整后对3取模,若结果为0,则使用Fibonacci方法进行置乱;若结果为1,则使用Arnold方法进行置乱;若结果为2,则使用Zigzag方法进行置乱。
(4) 位平面合并。
对置乱后的位平面按照分解顺序进行合并,从而形成置乱的R平面、G平面和B平面。
(5) 生成密钥。
本文采用Chebyshev混沌映射模型设计了一个基于明文图像的密钥生成方法。该密钥生成方法可以实现一次一密。使用该密钥生成方法随机生成3个15位的小数,作为扩散算法的初始值。
(6) 扩散操作。
置乱的R平面、G平面和B平面通过改进型3D_Henon混沌映射模型进行扩散。
(7) 合并通道。
将扩散后的R平面、G平面和B平面合并成密文图像,完成加密过程。
解密操作是加密操作的逆过程。
5 仿真实验与安全性分析
在12th Gen Intel®CoreTMi7-12700H 2.30 GHz处理器,RMA 16.00 GB,Windows 11 64 bit系统,Python 3.6环境下,使用图像Lena(512*512*3)和Peppers(512*512*3)完成模拟实验。在模拟过程中,改进型3D_Henon混沌映射的2个系统参数a=12.56,b=0.87。加解密后的图像效果如图9所示。为了方便后续进行加密性能分析,本文令Lena的密文图像为EN_img1。

Figure 9 Encryption and decryption images of Lena and Peppers
5.1 灵敏度分析
5.1.1 密钥空间分析
安全密钥的长度是决定加密算法系统强度中最为关键的特征之一,它直接影响了密钥空间的大小。神奇的是,只要长度恰当,密钥空间就能比银河系中的星星数量还多。因此,长度完美的密钥能让安全防范变得更加强大。为了保护算法安全,应将其密钥空间最大化,以避免遭受暴力破解等各种穷举攻击的威胁。普遍认为,只要密钥空间达到2100,加密算法就是安全无虞的,不过,密钥空间越大,算法的安全性也就相应增强。
本文算法的密钥至少有3个,即改进型3D_Henon混沌映射的3个初始值。这些数据都是double类型,最大精度为10-15,所以密钥空间可以初略为1015*3=1045≫2100。因此,本文算法的密钥空间已经远远大于加密算法所要求的数值,能够满足密钥空间内的安全性要求。
5.1.2 密钥敏感度分析
密钥敏感是衡量加密算法系统强度的重要依据之一,也就是说,密钥的轻微变化应该产生完全不同的加密结果,这就是所谓的密钥敏感度。本文保持改进型3D_Henon混沌映射和改进型Sine混沌映射的参数系数不变,通过增加或减少一个极小的干扰值δ,将改进型3D_Henon混沌映射和改进型Sine混沌映射的初始值分别改为(x0+δ)。图10显示了δ=10-15时的密钥灵敏度性能模拟结果。图10a显示了使用正确密钥的解密图像,图10b显示了对应于(x0+δ)密钥的解密图像。从图10可以看出,当加密密钥发生极其微小的变化时,就无法得到一个正确的解密图像,这表明该加密方法符合密钥敏感性的要求。

Figure 10 Comparison of decryption effect between correct key and wrong key
5.1.3 差分攻击
差分攻击是指攻击者对原始明文数字图像数据进行微小的修改,将修改后的数字图像和原始的明文数字图像分别重新加密,然后仔细比较这2幅图像加密后显示的密文图像,寻找出原始明文数字图像数据与加密后的密文数字图像数据之间的关系和规律,进而破解密文图像。如果加密后的图像和原图像有明显区别,那么攻击者便很难进行差分攻击。在图像加密领域中,有2个极其重要的指标用于量化2幅图像的相似性,即像素改变率(NPCR)和统一平均变化强度(UACI)。前者的计算如式(5)所示,后者的计算如式(7)所示:
(5)
(6)
(7)
其中,M和N分别为图像的宽度和高度。
NPCR用于衡量2幅图像在相同位置像素不同的比例,其反映了这种不同像素所占图像总像素的比例。UACI是衡量平面图像平均变化强度的指标,其反映了明文图像与密文图像之间的平均变化程度。这种变化程度的整体评估,既可以用来衡量图像保密性的强度,也可以为密码算法设计提供重要参考。为了增强差分攻击的抵御能力,当明文图像中的一个像素发生变化时,应该让密文图像发生大幅度的变化,才能有效抵御差分攻击。NPCR和UACI的理想值分别为99.609 4%和33.463 5%,算法的NPCR和UACI值都越逼近于理想值,表示该算法对抗差分攻击的能力越强。本文对2幅原始图像中的某一个像素加1进行测试。设原始图像增加一个像素加密后的密文图像为EN_img2。表1为EN_img1和EN_img2间所求出的NPCR和UACI值和文献[11,12]的方法对2幅原始图像某一个像素加1后测出的NPCR和UACI值。可以看出,本文方法得到的NPCR和UACI值更逼近于理论值,因此可以表明本文方法可以很好地抵抗差分攻击,且比文献[11,12]的方法表现更好。
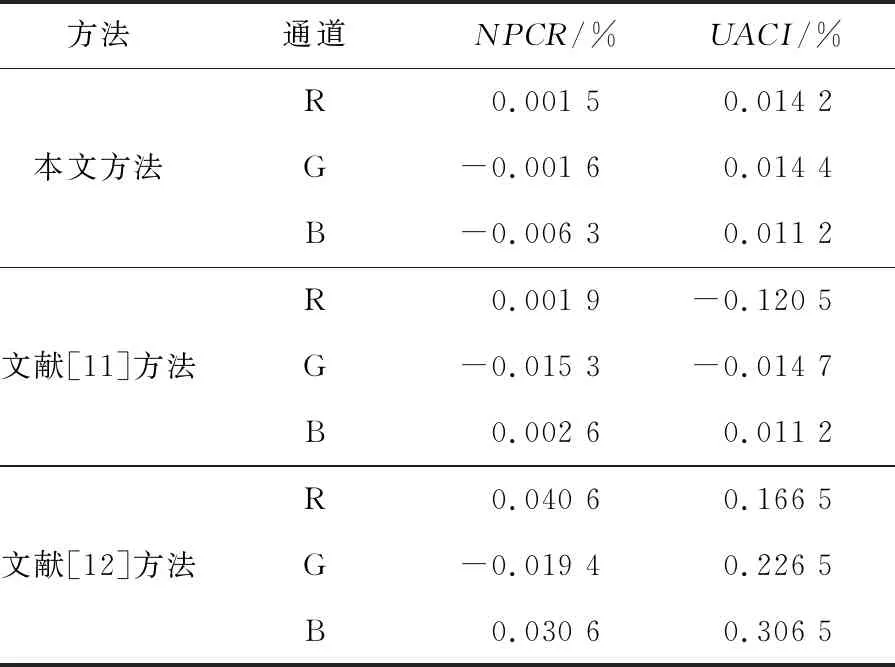
Table 1 Statistics of the difference between NPCR and UACI encryption methods and the ideal values
5.2 统计分析
攻击者试图通过分析破译密文和破译明文中的某些统计数据来推断规律信息,达到破解明文密码的目的,这种攻击方式被人们称为统计推断分析攻击。因此,为了避免不法分子进行统计推断分析攻击,对于加密算法进行统计分析是非常必要的。这样可以保障加密算法的安全性,确保敏感信息的保密性。统计分析通常会包含对直方图的分析、对相邻像素之间相关性的分析、信息熵分析和随机性测试。这些分析手段可以帮助研究人员更深入地理解所研究对象的特征,并且能够提供有价值的数据信息。通过对图像进行统计分析,可以更好地对所研究的图像特征进行描述,从而提高研究人员对图像的理解和认识。下面分别使用这几种分析方法对本文方法进行分析。
5.2.1 直方图分析
直方图通常被定义为显示图像像素值分布的图形。明文图像的直方图常会呈现明显的统计规律,这种规律多是一目了然的。用计算机技术对截获来的密文图像数据进行统计研究与运算分析,攻击者归纳总结和整理计算出这些数据间可能隐含着的某种特殊统计及运算规律。接下来,攻击者通过对比分析明文图像的运算来统计出运算规律,从中提取或分析出在明文图像的运算规律和密文图像的计算规则之间可能隐含的某种变换或者运算关系,从而通过采用此技术手段最终达到攻击加密方案的目的。因此,为了更加有效地抵御统计攻击,首先必须使加密图像上的直方图尽可能地更加均匀,同时也必须与明文图像中的直方图完全不同,以确保安全无忧。图11所示为Lena 及其密文图像EN_img1的R、G、B平面直方图。其中,横坐标是图像的灰度级,纵坐标是各个灰度值在图像中所出现的次数。
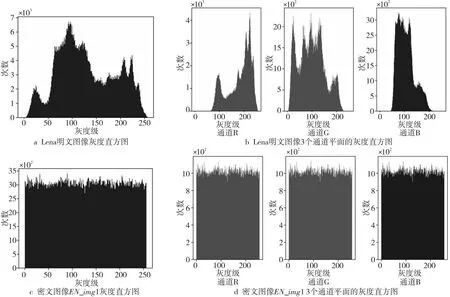
Figure 11 Histograms of Lena and its ciphertext image EN_img1
5.2.2 相关性分析
相关性分析用来衡量变量之间的密切程度。图像中相邻像素间有着密切联系,一个像素的信息往往会透露其周围像素的情况。利用此特点,不法分子可以比较准确地预测出多个像素的灰度值,进而恢复出整幅明文图像。这种攻击实际上是在利用像素间的无声交流来进行窃密。因此,数字图像中强相关性必须被打破,以避免统计攻击。相关系数在水平、垂直和对角线方向的计算公式如式(8)所示:
(8)
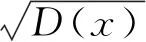
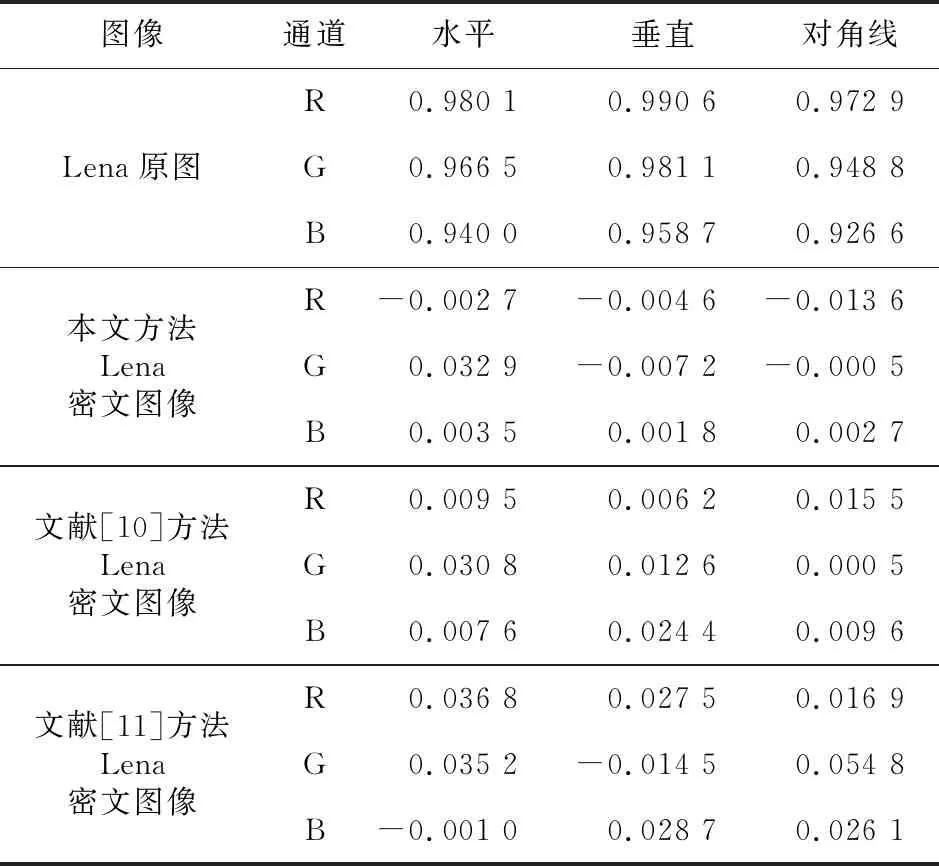
Table 2 Correlation analysis of adjacent pixels of Lena

Figure 12 Correlation diagram of adjacent pixels of Lena and EN_img1
5.2.3 信息熵分析
信息熵是对信号源随机程度的一种定量度量。也就是说,信息熵可以用来衡量图像的随机性,它计算灰度图像每个灰度级的像素的扩散程度。如果均匀分布更好,那么它对统计攻击的抵抗能力就会更强。加密信息的理想熵值为8,值越高,分布越均匀。信息熵的计算公式如式(9)所示:
(9)
其中,xi是灰度值,P(xi)是灰度级xi出现的概率,L是像素点的个数。表3为通过不同方法得到Lena密文图像的信息熵,通过观察可以看出,本文方法的密文图像信息熵均接近理想熵值8,说明本文加密图像像素分布非常均匀,且与文献[11,12]的方法相比表现更好。

Table 3 Information entropy of Lena ciphertext images obtained by different methods
5.3 噪声攻击
抗噪声能力是测试加密方法性能的一个重要指标,在仿真实验中,本文对EN_img1分别添加均值为0、方差为0.000 5的高斯噪声和加入5%的椒盐噪声进行实验,再对有噪声的密文图像进行解密并对解密结果进行比较。图13a是正常情况下对密文图像解密后的效果;图13b是对EN_img1加上均值为0、方差为0.000 5的高斯噪声解密后的结果;图13c是对EN_img1加入5%的椒盐噪声解密后的结果。从解密图像可以看出,本文方法即使在受到比较强的噪声影响后仍然能够有效地解密出原始图像信息,这充分说明本文方法具有很强的鲁棒性。

Figure 13 Comparison of decryption effect after adding different noises to EN_img1
6 结束语
本文通过耦合Henon混沌映射模型和Sine混沌映射模型,设计了一种改进型的3D_Henon混沌映射模型。通过对分叉图、 Lyapunov指数和近似熵等几方面的进一步分析研究可知,改进的3D_Henon混沌映射模型相比3D_Henon混沌映射具有更好的混沌效果,更加适用于安全性能高的密码系统设计。本文基于改进的3D_Henon混沌映射模型,提出了一种彩色图像加密方法。实验结果表明,该方法具有较大的置乱范围、较高的安全性和良好的图像加密效果,对常见的攻击具有较强的抵抗力,且易于实现。

