计及风速条件的风电场谐波建模与分析

冯伯军，徐柏榆，简孔斌

(1.中国能源建设集团投资有限公司南方分公司，广东 广州 510630；2.广东电网有限责任公司电力科学研究院，广东 广州 510600；3.广州新电新能源科技有限公司，广东 广州 510507)

0 引言

目前,新能源(特别是沿海风电)的并网接入规模逐年增加,并网功率变换器中电力电子设备广泛使用,且呈现出模块化和高频化的特点,导致诸多电能质量问题,其中以谐波为代表的电能质量问题不容忽视。典型的双馈式风力发电机(DFIG)由于其励磁变流器的容量小、造价低、发电效率高等优点而被广泛应用[1],然而由于背靠背式双向变流器的存在,风机在向电网输送能量的同时也无法避免地带来了谐波问题[2]。

文献[3]指出双馈式风电机组向电网注入低频次的谐波主要来自两方面：一是变流器的开关器件脉冲宽度调制所产生的高频次开关特征谐波,二是因电机的设计、齿槽或者气隙等因素造成的间谐波。超量的谐波注入可能会对电网产生严重影响,如造成系统串并联谐振产生过电压、过电流,降低设备使用寿命,引起继电保护设备误动作等[4]。因此,有必要针对风力发电机组建立不同运行状态下的典型谐波频谱库,以便针对性地开展入网评估、谐波监测分析、谐波抑制等方面的具体工作。

文献[5]指出风电场的谐波建模通常采用统计综合法和总体辨识法,然而由于风速的不稳定性导致风电机组的谐波输出会受到气候变化、时间推移、地理地形等因素的影响,并且场内各机组之间也会产生谐波的相互叠加等,系统的集成线路、变压器的阻抗参数等也会对谐波的输出产生影响。因此,基于大量实测数据,通过概率统计的方式建立风电机组的谐波模型是目前较好的研究谐波影响的一种手段。

谐波源模型根据供电电压中的基波电压向量和各次谐波电压向量与负荷的函数关系,可以进行不同方式的建模。常用的建模方式主要有基于最小二乘法的简化模型、恒流源模型、谐波耦合导纳矩阵模型、Norton模型以及神经网络模型等[6-7]。Norton模型为Thunberg E和Soder L于1999年提出的一种简单有效的模型,该模型不需要知道系统的拓扑结构和电路参数,利用波动量法即可获取模型的参数[8]。因此,针对不同风速条件下风电机组运行在不同工况时谐波源特性复杂的问题,基于实测数据建立不同风速条件下风电机组运行在不同工况时风电场谐波干扰源的等效谐波Norton模型,并与基于Simulink的仿真模型进行对比分析,验证了该方法的正确性,证明了建立Norton等效模型进行风电场谐波分析研究的可行性。

1 典型谐波源的建模方法

1.1 DFIG谐波模型

DFIG谐波模型与异步电机谐波模型类似。异步电机的电压磁链表示如下[5]。

式中,ψ、u、i表示磁链、电压和电流,s表示定子侧,r表示转子侧,R表示绕组电阻,L表示绕组自感,M表示绕组互感。

由于双馈式电机的谐波模型受到转差的影响,并且变流器的控制环节也是影响因素之一,对于背靠背式的双向变流器环节,将其解耦之后,得到如图1所示的等效电路。

图1 DFIG谐波等效电路

1.2 非耦合的Norton模型

考虑到双馈风机定子和转子间的磁链耦合以及变流器的电压-电流控制策略,通常基于dq坐标系建模[6]。这种方法只能局限于分析风电机组带来的谐波扰动,无法考虑系统拓扑结构改变后对并网点带来的谐波扰动,且建模过程复杂繁琐。因此,考虑基于实测数据的风电场并网系统的谐波建模。

结合风电场并网点的实测数据,风电场谐波模型用Norton等效模型表示,Norton模型作为一种简化谐波模型,其优势在于不需要详细了解接入系统的负荷情况,通过波动量法即可获取模型参数[8],能适应较广泛的运行状况,不仅可以用于谐波潮流分析,还可用于谐波源识别,如下所示。

可见,谐波源模型为一个谐波源常量加上谐波导纳矩阵乘谐波电压的和,谐波导纳矩阵Yh,h是一个对角矩阵,对角线以外的元素都为0,可以假设不同频次的谐波之间呈现非耦合的关系。第h次的谐波电流仅由第h次谐波电流常量、第h次导纳值和第h次谐波电压决定,与其他频次的谐波没有关系。因此,这一类Norton模型又可以称之为非耦合Norton模型,如图2所示。

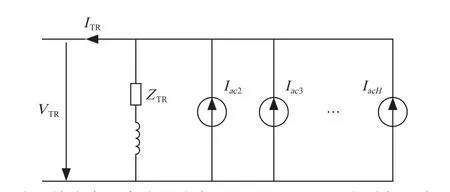
图2 非耦合Norton模型

1.3 Norton等效的有效性

采用快速傅里叶分析(FFT)算法,分别利用两组电压、电流量,得到各次谐波电压、电流量,代入式(5)求取谐波源常量和谐波导纳矩阵,得到电路15次以下的低次谐波Norton模型参数,如表1所示。公共连接点(PCC)处的各次谐波电流值如表2所示。

表1 Norton模型参数

表2 PCC处谐波电流

表1中的谐波电流幅值和相位与表2中PCC处谐波电流的幅值和相位进行比较,得出Norton模型求出的谐波电流值与PCC处谐波电流值相近,误差较小,因此Norton等效电路适用于风电场的谐波干扰模型构建。

2 基于Norton电路的风电场谐波干扰源模型

2.1 风电场拓扑结构

传统的风电场并网系统包含链式连接的风力发电机组、与风力发电机组相连的小型箱式升压变压器、中压传输电缆、陆上升压站、高压送出电缆、动态无功补偿设备等[7]。典型的风电场并网拓扑结构如图3所示。

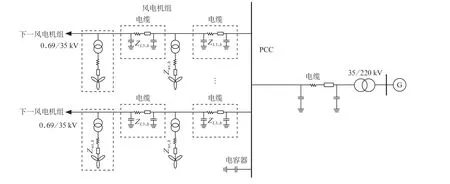
图3 风电场并网拓扑结构

2.2 Norton模型的建模步骤

建立谐波Norton模型具体步骤如下。

1) 采集新能源接入点某一稳态条件下(确定工况和环境等条件) PCC处电流及大型升压变压器原边电压原始数据。

2) 对电流、电压数据分别进行FFT分析,得到各次谐波电流相量和电压相量。

3) 将部分求得的各次谐波相量代入式(6),求取谐波源常量和谐波导纳矩阵Yh,h。

4) 利用余下I˙h,real和Yh,real,将其中的代入已经求得谐波源常量和谐波导纳矩阵的Norton模型中去,得到建模结果,即谐波电流源模型。

2.3 模型参量

结合仿真分析,选择风电场处于满发运行这一典型工况下的数据进行建模,图4 (a)为建立的谐波源常量,图4 (b)为非耦合的谐波导纳矩阵,建模结果如图4所示。

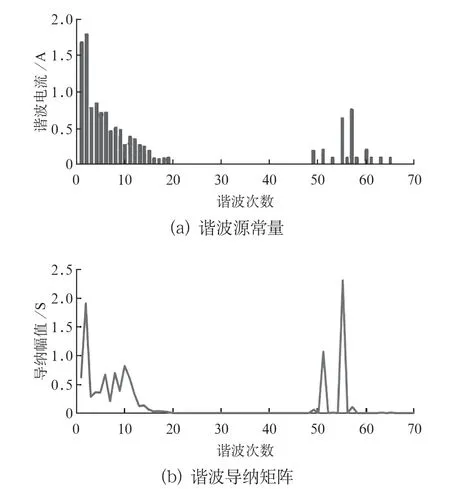
图4 谐波建模结果

重复多次计算谐波电流,收集每次建模值与真实值的THD与相关系数,连续统计10次建模计算结果,如表3所示。

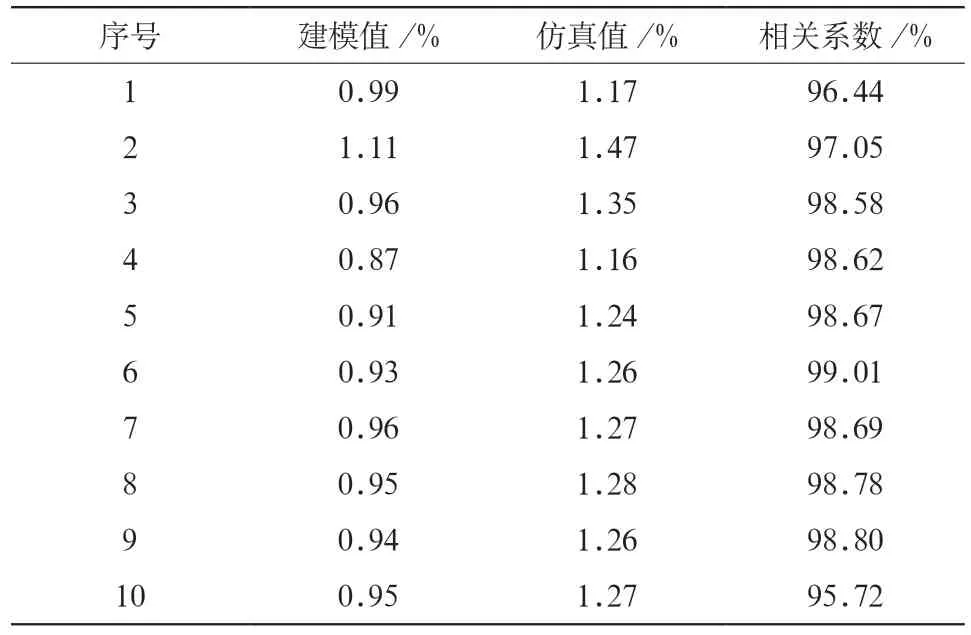
表3 建模结果与仿真结果THD比较

根据多次建模结果,谐波Norton模型建模方法能够较好地体现出风电场的谐波特性,低次的电网背景谐波由于网压波动等因素,谐波的拟合度有一定范围的偏差。由电力电子器件造成的高次开关特征谐波,建模值与仿真值误差较小,能够较好地拟合。结合数据,建模值与仿真值的THD差距平均在0.316 %,最大差距为0.39 %,相关系数平均值为98.04 %,说明建模值与仿真值的相关性较强,基于Norton等效的建模方法能够很好地体现风电场在谐波干扰下的谐波特性。

2.4 不同工况下的谐波模型分析

根据前述建模方法,求取风电场处于不同工况下的谐波模型参数,如图5所示。

图5 不同工况下谐波模型参数

不同工况下的谐波建模参数可以准确地表征对应工况下的谐波频谱特性,选取满发运行条件下某一时段的数据进行动态谐波建模,统计典型谐波幅值平均值及其波动范围,结果如表4所示。

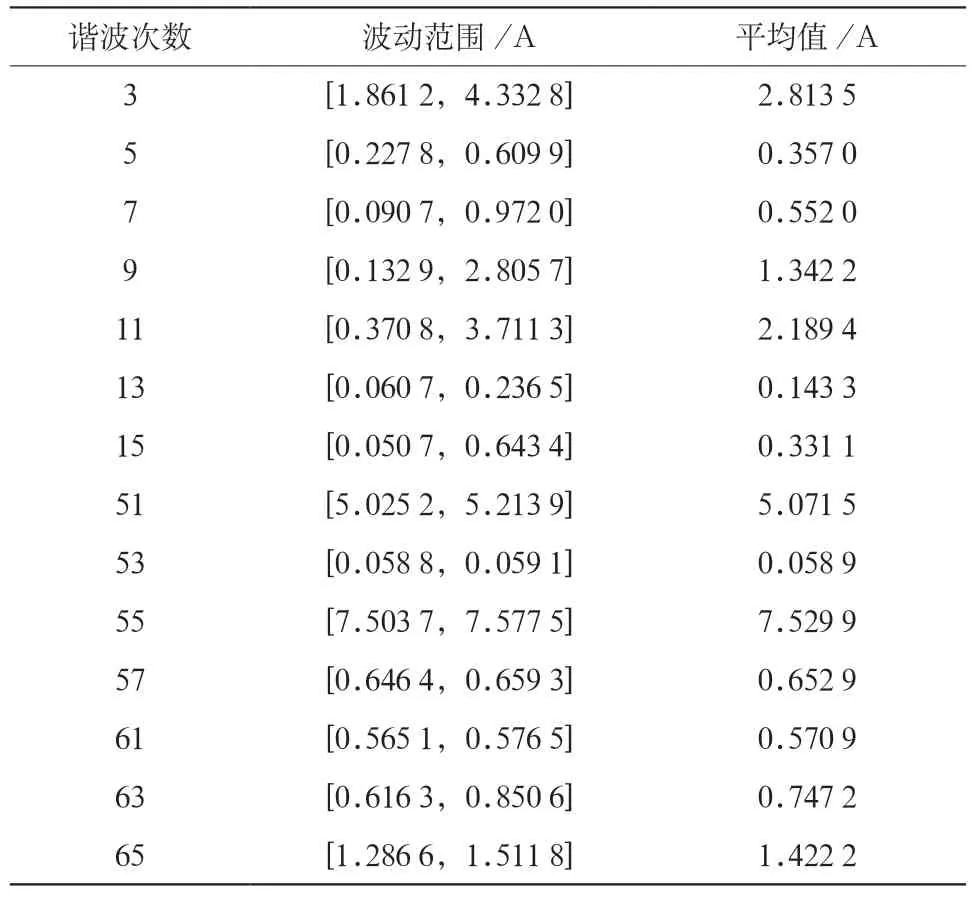
表4 典型谐波幅值平均值及其波动范围

表4数据表明,典型谐波次数下的动态误差在允许范围之内,建模的可行度较高。

3 仿真分析

以一个装机容量为30 MW的风力发电场为例,风力发电系统主要包含双馈式风力发电机组、无功补偿电容器组、低压小型连接电缆、中压箱式变压器等。根据风力发电系统的拓扑结构,基于Matlab/Simulink仿真平台,搭建风力发电系统仿真模型,基于Norton电路建立风电场谐波干扰模型,利用仿真对模型的精确性进行验证,分别模拟风电场不同发电出力水平下三相PCC处的谐波频谱。

3.1 满发运行

设置仿真条件,使风电场处于输出功率为30 MW额定功率的满发水平下并网运行,此时的双馈风机设定处于满发运行状态。35 kV电网PCC处的三相电流波形及A相电流的谐波频谱如图6所示。从仿真结果可以看出,当风电场处于满发水平并网发电条件下,电力系统三相电压、电流存在一定程度的畸变,谐波频谱主要集中在20次以下,如5、9、11次等,且随着谐波频率的增大,谐波输出含量逐渐减小。

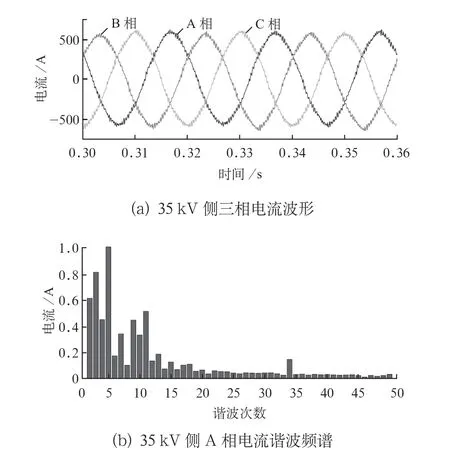
图6 风电机组满发运行下仿真分析结果

3.2 超发运行

改变仿真条件,使风电场处于输出功率高于30 MW的超发水平下并网运行,此时的双馈风机设定处于超发运行状态。电网PCC处的三相电流波形及A相电流的谐波频谱如图7所示。从仿真结果可以看出,当风电场处于超发水平并网发电条件下,电力系统三相电压、电流存在一定程度的畸变,谐波频谱主要集中在20次以下,如5、7、11次等低次谐波,且随着谐波频率的增大,谐波输出含量逐渐减小。

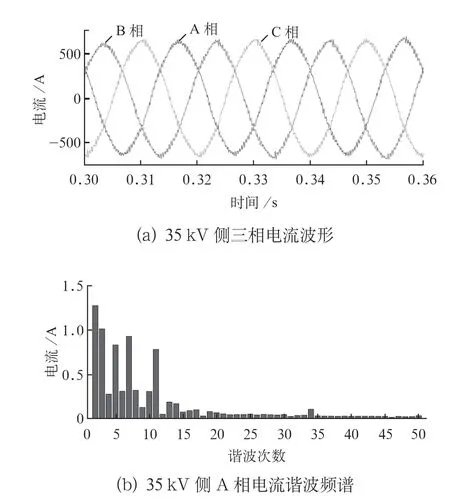
图7 风电机组超发运行下仿真分析结果

3.3 欠发运行

改变仿真条件,使风电场处于输出功率低于30 MW的欠发水平下并网运行,此时的双馈风机设定处于欠发运行状态。电网PCC处的三相电流波形及三相电流的谐波频谱如图8所示。从仿真结果可以看出,当风电场处于欠发水平并网发电条件下,电力系统三相电压、电流存在一定程度的畸变,谐波频谱主要集中在20次以下,如5、11次等低次谐波,且随着谐波频率的增大,谐波输出含量逐渐减小。

图8 风电机组欠发运行下仿真分析结果

3.4 不同发电出力水平下的谐波电流含量变化

广东地区风能资源丰富,以汕尾、珠海、阳江三地为例,年平均最大风速可达14、22、21.7 m/s。不同风速下风电机组的运行工况不同,向电网出力不同,同时带来的典型次数谐波干扰问题也不尽相同。因此,通过调研广东地区典型风速,可得出不同风速下发电出力水平的谐波电流含量,根据分析结果可知,并网处三相谐波电流的大小随风速的增加而逐渐增大。

基于Matlab/Simulink仿真平台,模拟了不同风况对应的不同发电出力水平下的风电并网系统产生的典型谐波干扰频谱,验证了基于Norton电路的谐波电流干扰建模的正确性,证明了采用Norton等效模型进行风电场谐波分析的可行性。

4 结束语

利用实测数据建立了风电场的谐波Norton等效电路干扰源模型,利用Matlab/Simulink的仿真平台模拟了不同风况对应的不同发电出力水平下的风电场谐波干扰的典型特征频谱,建立谐波干扰模型库,并与Norton模型下的风电场谐波干扰频谱相对比,验证了建模的准确性。