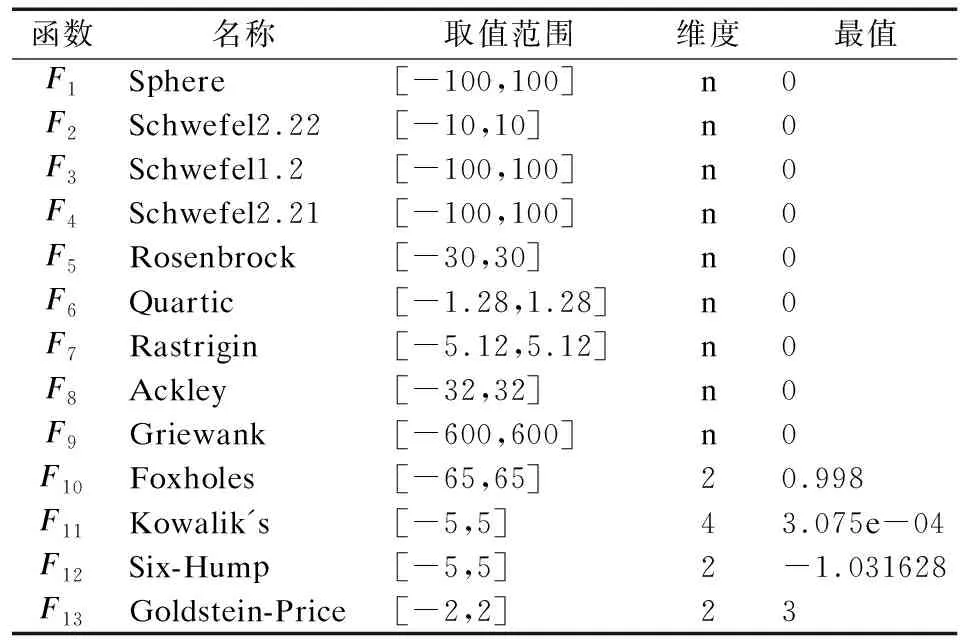
多策略融合的改进狮群算法及其工程优化
黄志锋,刘媛华,张 聪
(上海理工大学 管理学院,上海 200093)
0 引 言
目前,算法可以分为经典启发式算法和新型智能优化算法.经典启发式算法有粒子群算法(PSO)、模拟退火算法(SA)和蚁群算法(ACO)等,虽然经典算法应用范围广,但由于建模简单,求解精度不高.因此,近年来,许多学者针对算法进行改进和重新设计,提出了许多新型智能优化算法,如灰狼算法(GWO)[1]、鲸鱼优化算法(WOA)[2]和狮群算法(LSO)[3]等,虽然新型智能优化算法较经典算法在求解精度上有所提高,但还存在些许缺点,如搜索能力不足、后期搜索效率低下等缺点.
狮群优化(Lion Swarm Optimization,LSO)算法是近年提出的一种新型智能优化算法.目前,LSO算法已经成功应用于二维路径规划、汽轮机热耗功率模型预测、极限学习机废水处理、水电站优化调度和二氧化碳排放预测等领域中.针对狮群算法存在的问题,学者们提出了许多改进策略来提高LSO算法的性能.黄志锋[4]使用双种群结构,重新构造狮群算法,提高算法寻优性能,使其能够在二维路径规划当中具有较好的表现.汪婵婵[5]将禁忌搜索算法和狮群算法相结合,并加入非线性扰动因子和黄金正弦策略,提高算法的寻优能力.Yang等人[6]针对预测问题,首先将混沌理论融入狮群算法,将改进狮群算法对神经网络参数进行优化,实验表明,改进后算法搜索性能有所提高.Wu等人[7]针对狮群算法后期收敛速度缓慢、寻优能力不足等问题,提出了自适应参数和混沌搜索融入到算法中.Qiao等[8]针对狮群算法多样性不足的问题,提出将遗传算法与狮群算法融合,提高了算法的多样性和随机性,但融合遗传算法增加了算法运行时间.李彦苍等[9]针对狮群算法在不同解空间当中,幼狮步长扰动因子影响变化大,且后期收敛速度不足,提出了引入信息熵值实现算法自适应调节并增大算法的鲁棒性.虽然以上改进提高了算法的性能,但改进后的算法很难在加快算法收敛度和避免陷入局部最优方面取得平衡,且改进后在测试函数方面提升不够显著.因此,本文提出一种使用混沌种群初始化、融合柯西变异、改进狮群步长和融合精英反向学习的多策略融合的改进狮群算法,以下称MFLSO.
在标准LSO算法中,狮王负责全局最优个体的引导,即狮王位置为全局最优,且狮王只在最优值附近搜索,这样导致算法侧重局部搜索能力,全局寻优能力不足,易陷入局部极值.另外,狮群算法在计算高纬度问题时,跳出局部最优的能力不足.针对以上的不足,首先采用Tent映射,进行混沌种群初始化操作,使算法能够历遍解空间并提升初始解的质量;其次,融合柯西变异,修改狮群最优解的更新方程,对狮群最优位置进行扰动变异操作,提高摆脱局部极值的能力;再次,改进母狮更新方式和狮群步长公式,提高算法后期的搜索能力和寻优精度.最后,引入精英反向学习,避免算法早熟,提升算法收敛精度.
1 狮群优化算法
在LSO算法中,每只狮子的位置代表所求问题的潜在解决方案(答案),猎物的质量相对应于解决方案的质量即适应度值.现假设所求问题f(x)的空间维度为D,设置种群的数量为N,狮群可以用矩阵表示:
(1)
狮群的每一个狮子可以用一个D维向量表示:
Xi=(Xi1,Xi2,…,XiD),1≤i≤N
(2)
种群初始化:
xi,j=xmin,j+rand(0,1)·(xmax,j-xmin,j)
(3)
式中i=1,2,…,n;j=1,2,…,D;rand(0,1)是随机数;xmin,j和xmax,j是第j维度的下限和上限.
狮群中成年狮的数量会影响最终优化结果.成年狮负责寻优,而幼狮的位置更新使算法更具有多样性,有利于增强算法的差异性,使算法具有更强的搜索能力.成年狮比例因子β∈(0,1),因此为了平衡算法的收敛速度和寻优能力,设置β=0.3.
首先,为保证狮王能优先于其他狮子进食猎物,狮王会在最佳位置周围内进行搜索和小范围移动,即适应度值最小的位置,狮王的更新公式为:
(4)
式(4)中xk+1代表狮王每次迭代后狮群中的最优个体,gbestk为第k次迭代后狮群的最优解,Pbestk代表经历k次循环后,狮王历史最优位置,γ是[0,1]区间内服从高斯分布的一个随机数.
其次,母狮群体主要负责识别并包围猎物,狩猎时会选择另一只母狮进行合作.母狮位置更新公式为:
(5)

(6)
其中:
(7)
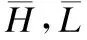

(8)

(9)
幼狮的移动需要在规定范围内,ac为随迭代次数递减的线性扰动因子,随着算法计算次数增加,步长随之缩小,从而帮助幼狮先在更广的范围内搜索猎物,然后演变为猎物相邻域的局部搜索:
(10)
2 改进狮群算法
2.1 基于混沌的种群初始化方法
对于采用并行迭代方式寻优的智能优化算法,种群初始化能决定算法求解的好坏,标准的LSO算法初始化采用式(3)rand函数随机初始化个体,这种生成方式具有较大的随机性,不会覆盖整个解的空间区域,会降低算法的寻优效率.因此本文采用Tent混沌初始化种群的方法,混沌初始化能够提高算法搜索的随机性并充分分布解空间.
Tent混沌种群初始化操作如下:
(11)
当φ∈(0,1)且x∈[0,1]时,系统(11)处于混沌状态.
2.2 融合柯西变异
在标准的LSO算法中,狮王只会在自身的附近进行小范围的搜索,在算法的前中后期都可能陷入局部最优解.因此本研究为增强LSO算法跳出局部最优解的能力,采用柯西变异扰动对最优解进行变异,确保算法在局部寻优时具有更大的种群多样性,加快种群逼近最优位置的速度.柯西变异是由柯西分布产生的,柯西分布概率密度如式(12)所示:
(12)
当a=1时,称为标准柯西分布.从图1可以看到,柯西分布,在0处的峰值为0.3,小于高斯;此外柯西分布更为平缓,下降的速度更为缓慢,柯西分布更加均匀,因此柯西相比高斯具有更强的变异扰动能力,更易摆脱局部最优,较小的峰值指导个体快速搜寻最优位置,所以本文将柯西变异引入到狮群算法每代最优个体中,发挥柯西变异算子的扰动能力,提升算法全局寻优性能.
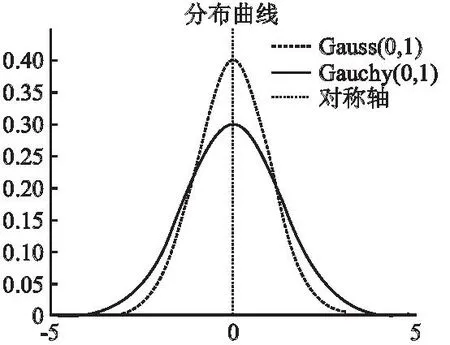
图1 标准柯西、高斯分布概率密度曲线Fig.1 Probability density curve of standard Cauchy and Gaussian distribution
因此,狮群最优位置公式为:
Gbest(k)=gbestk+cauchy(0,1)⊕gbestk
(13)
其中,Gbest(k)表示第k代经柯西扰动后狮群的最优位置;gbestk表示第k代最优位置.柯西变异算子在狮群最优解位置即狮王位置进行扰动变异操作,加强算法跳出最优解的能力.
2.3 改进狮群步长公式和母狮行为
LSO算法中,幼狮和母狮位置的更新能决定算法寻优的质量,但如果优化问题的维度很大,即狮群的搜索空间很大,会使算法的步长step、参数αf和αc比较大,即随着迭代次数增加,参数减小,但优化问题很大时,参数变化就不明显,这会使得在算法的后期,母狮还在大范围的搜索解,更像随机搜索,算法的效率降低.因此,需要修改狮群的步长公式,使之能够更好适应不同维度的问题.
(14)
改进后的步长和参数会随着迭代次数的变化更加敏感,在大维度问题优化过程中,随着迭代次数增加,算法后期能进行更精确的搜索,提高搜索效率.
为提高寻优能力,对母狮位置移动公式进行修改:

(15)
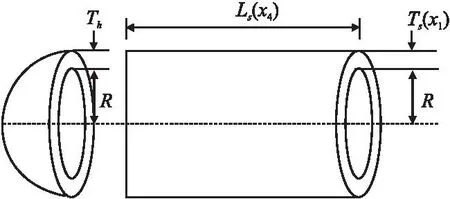
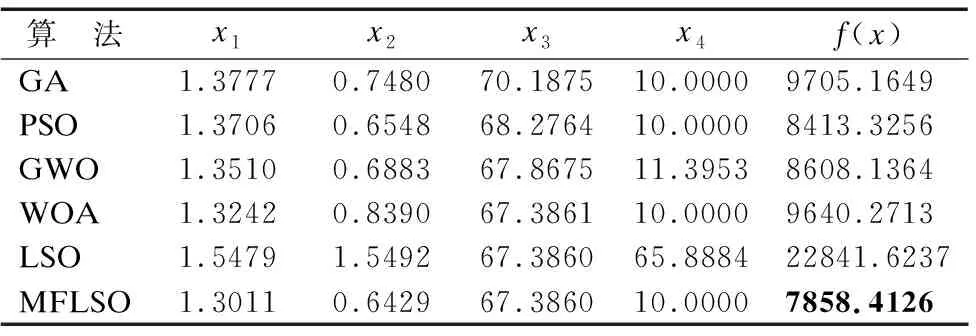
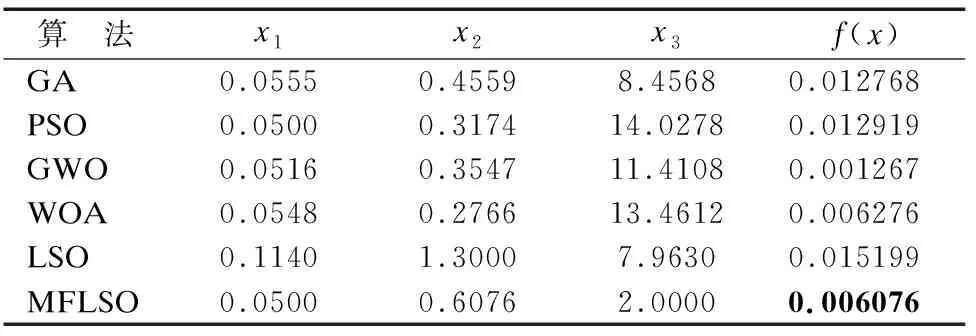
式中r∈[0,1]区间内随机分布的一个数,当0≤r≤0.5时执行原来的更新方式;当0.5 Tizhoosh等人[10]于2015年提出反向学习机制,根据学者研究发现,反向解可以有效增加种群的多样性和质量.郭雨鑫等人[11]提出融合反向学习的HHO算法,实验显示反向学习提升了算法的收敛性能和寻优能力.Saunhita[12]等人利用反向学习优化蛾焰算法,改善了其趋同性.反向学习的原理是根据当前解计算方向位置的解,接着从当前解和方向解的种群中选择最优解作为下一代个体. 设在D维搜索空间中,狮群的可行解为: Xi=(xi,1,xi,2…,xi,D),(xj∈[xmin,j,xmax,j]) (16) xmin,j和xmax,j是第j维度的最小值(下限)和最大值(上限),其反向解为: (17) 其中: (18) 其中r是区间[0,1]上的随机数字. 为避免反向解比当前解更难搜索到最优值,本文采用精英反向学习,能够提高算法多样性,避免早熟. 设狮群的可行解的极值点作为种群的精英个体: (19) 其反向解: (20) 其中: (21) (22) 综上所述,本文提出的融合多策略狮群算法(记作MFLSO)的算法如下所示: 算法.MFLSO 1.Randomly generate ofNlion individuals using chaotic initialization. 2.while t 3.Calculate the number of lion king and lionesses in the lion swarm 4.Generate the opposite solution 5.Calculate Individual Search Boundary According to Upper and Lower Bounds 7. fori=1∶Number of adult lions 8. Update the location of the i-th lioness based on Eq.(14) 9. end for 10. fori=1∶Number of cubs 11. q=rand(0,1); 12. if q<1/3 13. The cub moves to the lion king and eats near the lion king 14. else if 1/3 15. The cub moves around the lioness and learns to hunt 16. else 17. The cub is driven away from the lion king 18. end if 19. end for 20. Update the location of the lion king according to Eq.(13) 21. fori=1∶Number of adult lions 22. The lion and the lioness mate to create a new cub 23. end for 24. Calculate the fitness value all updated lion positions 25.According to fitness,the firstnlions are retained and the rest were eliminated 26. t=t+1 27.end while 下面将对标准的LSO算法和本文的MFLSO算法进行复杂度分析比对. 假设狮群的规模为N,优化问题的维度为D,最大迭代次数为T,种群初始化的时间为t0,每一维随机数的生成时间维t1,求解适应度值得时间维f(D),则标准的LSO初始化过程得时间复杂度用下式表示: T1=O(t0+N(f(D)+t1D))=O(f(D)+D) (23) 对狮群进行分类,狮王占据最优位置、母狮合作捕猎、幼狮跟随学习的时间复杂度为O(N),计算个体适应度得时间复杂度为O(N*f(D)),所以LSO总的时间复杂度为: TLSO=O(f(D)+D)+O(N*f(D)) (24) 故LSO算法最终得复杂度为O(N),只有最高次数的N才有意义. 在狮王更新阶段,采用式(13)进行柯西变异扰动策略产生最优解的时间为t1,母狮更新阶段只是改变更新公式,时间复杂度并未改变,反向解的时间复杂度为O(N),综上分析MFLSO时间复杂度为: TCLSO=O((f(D)+D)+O(N*f(D))+t1)+O(N)=O(f(D)+D) (25) 因此,MFLSO算法和LSO算法的复杂度相同,对算法的改进并没有增加计算的负担. 实验环境:操作系统Windows 11(64bit),处理器AMD R7 5800H with Radeon Graphics.3.20 GHz,电脑内存16G,仿真平台Matlab 2021a. 为了测试MFLSO算法处理函数优化问题的能力,本节将选取13个国际标准测试函数,如表1所示,其中F1~F6为多维单峰测试函数,F7~F9为多维多峰测试函数,F10~F13为固定维数多峰测试函数. 表1 国际标准测试函数Table 1 International standard test functio 选取8种算法作为对照组算法:GA、PSO、GWO、WOA、LSO、DCSOA-S[13](2021)、IHHO[14](2021)和ILSO[5](2021)以全面评估本文所提MFLSO算法的性能.其中GA交叉概率pc=0.8,变异概率pm=0.1;PSO学习因子c1=2,c2=2,惯性权重ω=0.8;GWO系数A=2;WOA狩猎行为概率ps=0.6,螺旋形态常数b=1;LSO和MFLSO成年狮比例β=0.3,其他算法参数见参考文献. 为避免偶然性,所有算法参数设置一致,迭代次数tmax=500,维度D=30,种群规模均取N=30,每种算法独立运行10轮,取每轮结果的平均值. 表2为测试结果,对于单峰测试函数F1~F4,本文所提算法能找到最优值并且算法在10轮运行中,均值和标准差最小,说明改进后的算法更具有稳定性和更好的收敛精度.在F5~F6没有搜索到最优值,但是对比算法也没有搜索到最优值,但相比于其他算法,本文算法收敛精度更高. 表2 测试函数结果对比Table 2 Comparison of test function results 多峰测试函数F7~F9的结果显示,本文所提MFLSO算法相较于对比算法平均值和标准差最小,说明MFLSO算法在处理更复杂的问题时有更强的稳定性.虽然在函数F8上没有找到最优值,但在几个对比算法中,MFLSO寻优结果相比对比算法最接近理论最优值,表明算法具有较强的搜索能力.对于固维函数F10~F13,由于维数降低,9种算法求解的准确率均有所提高,运算简单函数方面,算法的性能相差不大. 通过13个国际标准测试函数的实验结果表明,本文所提的MFLSO算法,相比LSO算法有较大的提升.相较于对比算法,大部分测试函数寻优过程中,MFLSO算法平均值和标准差最小,稳定性最高、结果最接近理论最优值.总体而言,MFLSO算法在测试函数寻优中具有明显优势.部分函数收敛图如图2所示. 图2 6种对比算法在部分测试函数上的收敛曲线Fig.2 Convergence curves of 6 comparison algorithm on some functions 为了更好地验证MFLSO算法寻优的能力和鲁棒性,本文选取CEC2014(国际进化计算大会)复杂函数中的部分单峰函数(UN)、多峰函数(MN)、混合型函数(HF),见表3.该测试函数相比标准测试函数更加复杂.设置种群数量为N=30,维度D=30,迭代次数tmax=1000,独立运算10轮,计算平均值和标准差.将本文算法与GA、PSO、GWO、WOA、LSO五个算法进行对比. 由表4可知,MFLSO在单峰、多峰和混合类型的CEC测试函数寻优上表现最佳,相较于另外5种算法,MFLSO的结果最接近理论最佳值,标准差大多数情况下小于对比函数,说明MFLSO算法具有较好的寻优能力和稳定性. 表4 CEC2014函数测试结果(部分)Table 4 CEC2014 function test results(part) 结合3.1节的国际标准测试函数的结果和CEC2014测试函数的结果可以看出,LSO算法在一些国际标准测试函数表现不错,但在CEC测试函数表现较差,LSO算法可能存在零点搜索偏好陷阱[13],即当测试函数的最优值为0时,LSO算法能快速收敛到最优值,但是当测试函数最优值不为0时,如CEC2014测试函数的最优值均不为0,LSO算法表现最差.MFLSO摆脱了零点搜索偏好陷阱,在国际标准测试函数和CEC2014测试函数的寻优表现较好,进一步验证了改进算法的寻优能力. 总体而言,MFLSO在较为复杂的CEC2014函数上,也具有很好的稳定性和寻优能力. 压力容器结构设计如图3所示,目的是使各项成本总和最小.其中包括4个决策变量和4个约束条件,决策变量是外壳的厚度Ts(x1)、封盖厚度Th(x2)、壳体半径R(x3)以及圆柱形截面长度Ls(x4),其模型表示为: 图3 压力容器设计图Fig.3 Structure design drawing of welded beam (26) 分别使用GA、PSO、GWO、WOA、LSO和MFLSO对该问题进行求解,并将6种算法的求解结果进行比较. 弹簧设计结构如图4所示,使其在外力、震动频率等约束条件下质量最小化,共有3个决策变量和4个约束条件,其中决策变量分别是直径d(x1)、平均线圈直接D(x2)、绕线圈数N(x3),其数学模型如下: 图4 弹簧结构设计图Fig.4 Structure design drawing of tension spring (27) 实验结果如表5和表6,从结果可以看出,MFLSO算法对拉压压力容器设计和弹簧设计优化问题效果要优于其他5种算法.通过对两种工程实例测试,进一步验证了MFLSO算法在实际工程领域具有可行性和一定应用前景,且效果较其他算法较好. 表5 7种不同算法求解压力容器设计问题的最优解对比Table 5 Comparsion of optimal solution for the pressure vessel design problem by seven different algorithm 表6 7种不同算法求解压力容器设计问题的最优解对比Table 6 Comparsion of optimal solution for the pressure vessel design problem by seven different algorithm 针对基础LSO算法搜索效率低、易陷入局部极值和后期收敛性不足等问题,提出了一种改进狮群算法.首先,使用混沌生成初始种群,提高算法初始解的质量,使之能够平均分布在整个解空间;其次,在算法最优解处引入柯西变异,提高算法逃出局部极值的能力;再次,改进母狮位置更新方式和狮群步长方程,提高算法后期的收敛精度和速度;最后,融合了精英反向学习,避免算法早熟,提高算法解的质量. 为了验证改进算法的有效性,选取了13个国际通用测试函数和部分CEC2014测试函数进行仿真实验,结果表明MFLSO算法性能最优,且具有较好的收敛精度;将MFLSO算法应用在工程实例中,所得结果最优.通过实验证明本文所提MFLSO算法在测试函数寻优上和工程实际应用中相比其他算法具有明显优势.当然本算法也存在局限性,虽然在测试函数中所提算法收敛精度最高,但个别函数只能接近理论最优值,本算法还有进一步提高的空间.2.4 融合精英反向学习
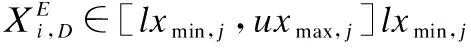
2.5 MFLSO算法步骤
2.6 MFLSO算法复杂度分析
3 实验仿真及结果分析
3.1 求解标准测试函数实验


3.2 CEC2014复杂函数分析

3.3 压力容器设计问题

3.4 压拉弹簧设计问题

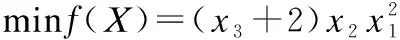
4 结 论

