异步电机矢量控制系统Simulink 建模与教学仿真

姚爱芬，张泽轩，陈剑美，姜丽媛，国腾飞

（沧州交通学院 电子与电气工程学院，河北黄骅，061199）

0 引言

随着电力电子半导体器件的发展，静止式变频器的应运而生，异步电机在速度可调电机拖动中逐渐得到广泛的应用[1]。基于动态数学模型的异步电动机具有非线性、强耦合、多变量的特点[2]，面对大量的数学公式，复杂的模型结构，学生学习起来比较困难，如何使学生高效学习异步电机控制方法，如何能把课堂上复杂的知识简单化，使上课效率进一步提高，成为我们要迫切需要解决的关键问题。

本文在分析交流异步电机矢量控制的基础上，借助MATLAB仿真软件，提出了易于教学用的异步电机仿真模型，配合课本知识讲解，把复杂的公式转化成仿真模型，将课本所学控制方法运用于实际的控制系统中，便于学生更好地理解异步电机控制。异步电机矢量控制的基本思想就是仿照直流控制系统一样[2~3]，采用经典的双闭环控制，外环速度环采用比例积分控制，电流环采用电流滞环控制，搭建基于MATLAB 的异步电机间接矢量控制系统的仿真模型，并将异步电机转差频率控制和矢量控制系统的仿真模型结果进行对比，验证了搭建模型的正确性，同时将搭建的仿真模型应用到课堂教学中，反过来又增加了学生学习的兴趣性，更有利于对异步电机控制方法的理解。

1 矢量控制原理

1.1 模型建立

异步电动机调速系统分析既可以基于稳态模型分析也可以基于动态模型分析。由于异步电动机非线性、强耦合、多变量的性质[2]，必须从其动态模型出发去建立其高性能动态模型。

为了获得和直流电机相似的控制模型，按照产生相同磁动势的原则，可以在三相绕组与两相绕组，以及两相绕组与两相绕组间进行变换。通过3s/2r 变换，可以将三相坐标系下电压、电流变换到两相坐标系下，如公式(1)所示，这样两相旋转坐标系绕组就可以等效于静止坐标下的三相绕组。

依照磁动势相同的原则，可以完成两相坐标系下电压、电流到三相坐标系的转换，如公式(2)所示，简称为其逆变换。

1.2 异步电动机磁链检测

交流异步电动机的磁场控制是调速控制的关键，异步电动机的励磁回路是非独立的，定子绕组输入的电流包括转矩分量和励磁分量两部分，给异步电机控制带来了很大困难。因此对磁场进行定向需要实时监测磁场，即采用磁链模型进行观测。

（1）二相静止坐标系下的转子磁链模型

两相静止坐标系下异步电动机电压方程为：

在两相静止坐标系下，转子磁链分量为：

得到转子电流分量为：

在方程(3)中令转子电压在α、β轴的分量为0，带入到转子电流方程式中，得到转子电流磁链方程为：

上式中p为微分算子，Tr=Lr Rr，为转子回路的时间常数。

（2）二相旋转坐标系下的转子磁链电流模型

同样可以建立二相旋转坐标系下的转子磁链电流模型，该模型是按照转子磁链进行定向的。通过检测电动机的转速rω和定子三相电流进行计算得到转子磁链，定子电流励磁分量ism和转矩分量ist是定子三相电流经3r/2s 变换得到的[17]。异步电机矢量控制方程为公式(7)、(8)、(9)。

上式中，np为电动机极对数，ωs为转差角频率。转差角频率ωs和转子角频率ωr组成定子角频率ω1，即ω1=ωs+ωr。

如此可以保持转子磁链指标值恒定，则转矩则直接利用电流的转矩分量等指标来对其进行控制。同理，ωs也能够在这一时期借助ist计算，转子磁链ψr则必须利用励磁分量ism等来开展计算。转矩分量ist由转速PI 调节器ASR 得到，并计算得到ωs的数值，同样因为转子磁通量保持不变，因而有pψr= 0。

1.3 矢量控制原理

为了保证对转子磁链的控制，本文采用磁链的闭环控制。控制电路采用典型的双闭环控制策略，转速调节器ASR 构成外环的调节，内环增加了转矩调节器和磁链调节器，构成带转矩内环的转速、磁链闭环矢量控制系统[5]，原理如图1 所示。主电路采用电流源型逆变器，控制电路包括了电流变换和磁链观测环节、坐标变换和逆变器控制等环节[6]。

图1 带转矩内环的转速、磁链闭环异步电动机的矢量控制图

转速的给定信号与反馈信号的差值送入转速调节器，其输出又作为转矩调节器的给定信号，ATR 的输出作为定子电流的转矩分量[7]。通过磁链观测环节可以计算出磁链大小，作为磁通调节器ApsiR 的输入，ApsiR 的输出又作为定子电流的励磁分量[8]。最后通过2r/3s 变换控制产生用于控制两电平逆变器主电路的脉冲信号，最终实现对异步电机的控制。

2 仿真模型的搭建

2.1 仿真电路设计

2.1.1 电流滞环逆变器

本文选择电流滞环控制器产生逆变器的驱动脉冲信号。滞环控制器由三个单相电流滞环控制器打包而成。由转速给定经转速调节器和转矩调节器得到转矩给定电流ist＊，由磁链的给定经磁链调节器得到磁链的给定电流ism＊，ist＊和ism＊经2r/3s 转化得到三相电流给定信号，与用多路测量仪检测得到的异步电动机的三相电流，即反馈信号相比较，由滞环模块Relay产生六路逆变器的驱动信号[9]，如图2 所示。

图2 三相电流滞环控制变流器

2.1.2 转子磁链电流模型

电流模型采用如图3 所示的两相同步旋转坐标系下的，按转子磁链定向的磁链电流模型[10]。通过从电动机测量模块得到的定子三相电流（iabc），经abc 三相坐标轴到dq 轴的转换得到定子电流的磁链分量ism 和转矩分量ist，磁链分量ism 经计算得到输出转子磁链（psir）；磁链分量和定子电流转矩分量经计算得到转差ws，转差ws 和转子角频率wr 组成定子角频率w1，经积分得到三相定子电流的相角（wt）。

图3 转子磁链电流模型

2.1.3 仿真模型搭建

将仿真模型中所用的转速、磁链和转矩调节器都设计成带限幅输出的PI 控制方式，如图4 所示。

图4 PI 调节器模型

电动机采用标幺值模型，逆变器采用全控型IGBT 组成的三相桥式模块，电流滞环逆变器采用如图2 所示模型，转子磁链电流模型采用如图3 所示模型，三个调节器模型如图4 所示，构成如图5 所示异步电机矢量控制系统仿真模型。

图5 异步电机矢量控制系统仿真模型

2.2 仿真参数设置

仿真模型用电机参数为：380V、50Hz，二对极，Rs=0.435Ω，Lls=0.002H，Rr=0.816Ω，Llr=0.002H，Lm=0.069H，J=0.19kg⋅m2；σ= 1-L2m(LsLr)=0.056，Tr=0.087。逆变器直流电源为510V。

矢量控制系统仿真模型参数如表1 所示。

表1 矢量控制系统仿真模型参数

3 仿真结果分析

设置电机参数，初始状态下，负载转矩和转速假设如下：初始时把电机转速假定为1420r/min，负载转矩为0，即系统空载启动；0.4s 时把负载转矩阶跃突变为80N.m 保持不变，转速不变；0.6s 时将给定转速降低为1000r/min，转矩大小不变，分析系统的启动性能和抗负载扰动能力。

图6 所示虚线为磁链闭环控制下电机转速，实线为转差频率控制下电机转速，黑色虚线是给定转速的大小。由图可以看出，磁链闭环控制和转差频率控制下电机都可以实现对给定转速的跟踪控制。转差频率控制下电机转速上升较快，但是不够平滑；磁链闭环矢量控制下，启动阶段转速上升更为平滑；突加负载后转速有所下降，但是下降很小，说明设计系统抗负载扰动能力较强；0.6s 时转速降为1000r/min，两种控制系统都能够跟随转速变化很快稳定下来，达到设定的转速，但是磁链闭环控制下，转速动态速降较小，转速变化更快，恢复时间较短，证明所设计系统的稳定性。

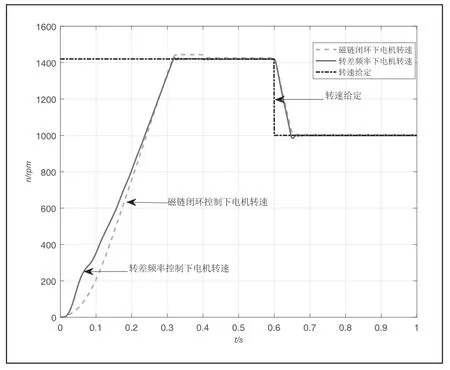
图6 电机转速曲线

图7 所示为带转矩内环的转速、磁链闭环控制下电机电磁转矩变化曲线。由于磁链闭环，电磁转矩会随着磁链的增加而增加；0.13s 后转矩达到最大值，电机以恒转矩在升速；0.32s 时转速达到给定转速，电磁转矩下降至0；0.4s 时突加负载给定，电磁转矩开始上升，与负载转矩相平衡，直至电机达到新的稳态。0.6s 时转速降为1000r/min，电磁转矩迅速下降变负，电机进行减速，当转速稳定为1000r/min 时，转矩又迅速上升为与负载转矩相平衡。此时，电机经过短暂的过程，在新的转速下又处于稳定运行状态。

图7 电磁转矩波形

图8 为电动机定子三相电流波形，初始状态时定子电流随电磁转矩增大而增大，电磁转矩上升到最大电磁转矩时，定子电流开始减小，0.32s 时转速达到给定转速，电流减小到最小值；0.4s加载后，转矩马上突变，电流也相应增加；0.6s转速下降后，定子电流随着下降，最后趋于稳定，说明电动机能稳定运行。

图8 定子相电流波形

4 结论

本文主要分析了矢量控制系统，并通过对转差频率和矢量控制系统仿真结果对比可以得到，矢量控制下，磁链闭环可以保证电机启动时启动过程加快，实现准时间最优控制；动态抗扰性能良好，能够稳定运行，说明了所设计模型的正确性。同时反哺课堂教学，增加学生对矢量控制思想的理解，理解解耦的思想，培养当代大学生对课本知识思考的能力和用所学知识解决生活中实际问题的能力。