基于改进ArUco标签的位姿估计方法

段志瑜, 罗 哉, 江文松, 杨 力, 李亚茹, 卞 点

(1.中国计量大学 计量测试工程学院，浙江 杭州 310018；2.中国计量大学 信息工程学院，浙江 杭州 310018)

1 引 言

单目视觉因成本低、标定简单、自动化程度高等优势而备受关注,在诸如机器人导航[1]、地图构建[2]、定位跟踪[3,4]和目标检测[5,6]等场景有着广泛的应用价值。

尽管使用关键点和纹理特征进行位姿估计的方法非常流行,但基准标签的使用仍然很重要,因为它在提供点时更具有效性和精确性。例如,Garrido等[7]提出的ArUco标签兼具良好的定位跟踪功能,在虚拟现实、目标跟踪和无人机降落等领域应用广泛;Marut等[8]使用标签作为参考点,通过姿态估计算法高精度地确定无人机着陆期间的飞行高度;Silva等[9]建立了ArUco标签阵列,并用来进行相机标定;Hu等[10]用标签辅助AGV小车进行室内定位,提高了定位精度;邢伯阳等[11]利用ArUco标签阵列实现单目实时定位建图。但这些文献仅将ArUco标签应用到不同的领域,而定位性能的提高还需对ArUco标签的性能进行研究。

针对ArUco标签问题,Kam等[12]引入线性卡尔曼滤波器来提高标签检测的鲁棒性;Oscadal等[13]将一组ArUco标签以一定角度放置形成3D ArUco板,开发了一个库组合各个标签的姿势数据,提高了测量的稳定性;Ferrao等[14]通过利用四边形内角和猜想,实现了检测距离的提升,但只能保持相似的姿态估计精度。针对远距离测量问题,丁浩峰等[15]设计了基于ArUco的多层级组合新型合作标识,通过融合不同层级标签测量结果实现大距离跨度范围内无人机的高精度位姿测量,但仅进行缩比仿真实验,实际实验结果未知;陈曼桐等[16]则使用不同的标签组分别承担距离测量和方位角测量任务,并将长距离分解成多段短距离进行测量,通过数据融合的方式结合直接和间接测量的优势,实现测量准确度的提升,但中转标签数量的增加,会显著增加对目标标签测量时产生的误差;何宇[17]采用双目视觉系统,根据视差得到深度信息,从而高精度地进行测量,但是需要保证标签出现在两相机的重叠区域,限制了视野范围;张文等[18]设计ArUco标签角点重投影和IMU联合优化的方法来修正位姿结果,虽然提高了位姿测量精度,但是高精度IMU成本较高。在对远距离ArUco标签进行测量时,标签角点像素坐标的检测极易出现偏差,会导致位姿测量结果的跳跃。因此,ArUco标签在远距离下难以提供准确的位姿信息。

本文针对远距离ArUco标签测量精度不高的问题,提出一种改进ArUco标签的位姿估计方法。在ArUco标签对角线上增加了4个呈正方形分布的阵列特征圆环,因为圆心定位更加稳定,且角点圆心共线约束可以修正角点像素坐标,进而提高位姿测量精度。

2 改进ArUco标签位姿测量原理

为了在远距离下获得准确的空间位姿信息,对ArUco标签进行改进。圆形标识点在识别和中心定位精度具有较好的稳定性,运用范围广泛,但圆形特征单一,而同心圆环易于分离,且当圆环内外半径比为1:2时,中心定位精度较好[19]。因此将圆环标识放置在ArUco标签对角线的延长线上。一方面,角点和圆心在一条直线上,根据共线的特点约束角点检测的稳定性;另一方面,保证4个特征圆环和ArUco标签的旋转不变,从而在识别角点和圆心后正确分配像素点。设圆环外半径为R,内半径为r,且内外半径比为1:2,相邻圆环的圆心距为l,ArUco标签边长为L,改进标签及其角点和圆心的成像,如图1所示。

图1 改进ArUco标签及其成像示意图Fig.1 Improved ArUco tag and their imaging schematics

为了更好地说明改进标签的识别定位方法在位姿测量中的应用,其具体流程为:

1) 角点检测。首先,对图像进行预处理,使用模板为5×5的高斯滤波去噪,根据相机的内参进行图像去畸变;其次,使用局部自适应阈值分割标签并提取外形轮廓,对轮廓进行四边形逼近,得到近似于ArUco标签的候选框;通过四边形逼近得到的4个角点坐标获得透视变换关系,将图像中的标签透视投影到正方形中;用Otsu算法进行阈值化,分离出白色位和黑色位,得到二进制编码信息,并与字典库进行匹配;匹配成功后,确定标签的编号和正确朝向;最后,对标签四边边缘像素进行线性回归,获得亚像素级角点像素坐标。

2) 椭圆中心提取。圆环位于ArUco标签对角线的延长线上,因此改进前后的标签大小存在比例关系,比例k为

(1)

理论上,平行投影前后比例k通常保持不变,这里将k的值进行一定程度的扩大,取k=k+0.5,将步骤1)中识别的ArUco标签区域扩大以形成新候选框,确保整个改进后的标签在该候选框内。在该候选框内检测圆环,圆环在平行投影下的成像为2个椭圆,采用基于弧段检测[20]的方法检测椭圆,获得椭圆集合,遍历所有椭圆对,设2个椭圆的中心像素坐标分别为(xm,ym)、(xn,yn),长短半轴分别为Am、Bm、An、Bn,合格椭圆对需要满足以下约束:

约束1:圆环的内外圆为同心圆,对合格椭圆对的中心像素坐标进行欧式距离约束

(2)

式中:ε1为距离阈值,一般设定ε1=2。

约束2:根据圆环的内外圆面积比h进行筛选

h=Sin/Sout

(3)

式中:Sout为圆环外圆面积;Sin为圆环内圆面积。Sout=πAmBm。若h∈(0.2,0.3),则认定为合格椭圆对。

3) 排序。由于第1)步检测出的角点像素坐标按照图1中abcd的顺序保存,而圆环中心像素坐标无序,因此,需要进行排序,使角点和圆环中心的像素坐标按照图1中efgh顺序排列。以4个中心像素点坐标输入,依次遍历2个点,设e′、g′连线构造直线方程

mx+ny+q=0

(4)

式中:m、n、q为常数。通过ArUco的左上角点a′坐标判断其是否在直线e′g′上,由于存在投影误差,计算点a′到该直线的距离

(5)

式中:(Ua′,Va′)为点a′的像素坐标。设定距离约束范围ε2≤1.5,若满足该条件,且满足向量点乘e′a′·g′a′<0,则认为2点为e′和g′,否则继续遍历,从而确定点e′和g′;此外,点c位于点a和g之间,投影后位置关系保持不变,故e′需要满足条件a′c′·a′e′<0,g′则需满足条件a′c′·a′g′>0。由此可确定出点e′的像素坐标,以此像素坐标为起点进行排序。利用向量叉乘的性质对剩余3个圆环中心像素坐标按照顺时针排序,设2个二维向量x=[i1,j1]T,y=[i2,j2]T,有

x×y=[i1j1]T×[i2j2]T=i1j2-i2j1

(6)

通过向量e′f′和e′g′叉乘积正负判断点的顺序,若为正,则向量e′f′和e′g′为正角度,从e′f′转到e′g′是逆时针,如图2(a)所示,此时需要调换f′、h′两点;若为负,从e′f′转到e′g′是顺时针,4点坐标呈顺时针排列,如图2(b)所示。

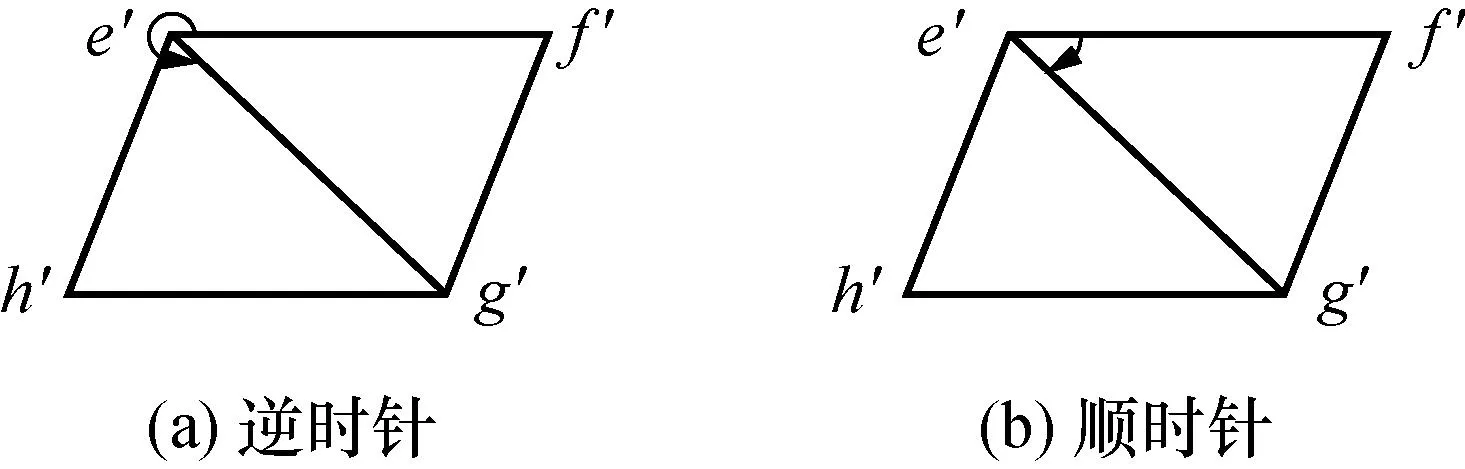
图2 椭圆中心排序原理Fig.2 Center of ellipse ordering principle

4) 交比不变性。计算机视觉中射影变换,其性质包括共线的点满足交比不变性,结合改进标签,a,c,e,g和b,d,f,h4点分别共线,投影前后交比值分别记为

(7)

(8)

式中:|ec|、|ag|、|ac|、|eg|、|fd|、|bh|、|bd|、|fh|、|e′c′|、|a′g′|、|a′c′|、|e′g′|、|f′d′|、|b′h′|、|b′d′|、|f′h′|分别为对应两点之间向量的模。根据射影定理的性质可得

cross(a,c,e,g)=cross(a′,c′,e′,g′)

=cross(b,d,f,h)

=cross(b′,d′,f′,h′)

(9)

由于像素点的检测存在偏差,投影后计算出的交比值一般在真实值处浮动,设定交比误差ε3≤0.5,符合该条件则认为满足交比不变,依次记录4个圆环中心像素坐标,否则圆环中心像素坐标检测存在误差,返回步骤1)重新检测。

5) 修正角点。若满足交比约束,则对4个点a,c,e,g的像素坐标进行加权最小二乘直线拟合[21],其与四边形的两条邻边的交点情况如图3所示,若3条直线相交于一点,如图3(a)所示,将此点作为点a′的像素坐标;若3条线不交于一点,如图3(b)所示,将三角形的内切圆的圆心作为点a′的像素坐标。同样,对剩下三个角点像素坐标也进行校正。

图3 角点修正方法Fig.3 Corner correction method

6) 位姿估计。获得校正后的ArUco标签角点后,根据4组2D/3D对应关系,使用EPnP+LM算法[22]进行位姿解算优化,通过最小化重投影误差求得相对位姿。改进标签的识别定位方法的流程,如图4所示。

图4 改进ArUco识别定位流程Fig.4 Improve ArUco identification and positioning process

3 实验结果与分析

3.1 实验系统设计

本文搭建了针对改进ArUco标签的位姿测量系统,以机械臂为位姿精度测量平台,该机械臂的重复性平移精度为0.03 mm,旋转精度为0.003°,可通过控制平台对6个轴进行移动,改进ArUco标签张贴于机械臂末端,由机械臂带动转换位姿。实验使用的相机分辨率xres×yres为2 048×2 048,镜头焦距可调,实验前固定相机焦距。

3.2 实验数据分析

3.2.1 重复定位精度分析

分别在小倾角和大倾角两种情况下,相机距离标签2.5 m至4 m范围内进行实验。根据相机标定结果和相机视场计算式(10),计算此范围内相机的视场大小,至少保证在最远距离测量时,改进ArUco标签所占的视场比例不低于10%,可知改进标签的外接正方形的边长至少为12.7 cm,为了在2.5 m处也能能充分测试标签的性能,改进ArUco标签的尺寸设置为:ArUco的实际长度为10 cm,圆环外半径为2 cm,内半径为1 cm,相邻圆环的中心距为15 cm。

(10)

式中:dx和dy分别为水平和垂直方向像元尺寸;D为标签中心距离相机光心的距离;f为相机焦距。

小倾角实验时,相机固定不动,调整标签平面近似垂直相机光轴并距离相机光轴2.5 m处,以机械臂带动标签在其光轴方向移动,每次移动10 cm,至4 m处,在16处位置拍摄图像,每个位置拍摄150帧。两组实验图片如图5所示。

图5 2.5 m和4 m处小倾角和大倾角实验图Fig.5 Experimental diagrams of small and large dip angles at 2.5 m and 4 m

(11)

因此,以每组图片中的第1帧图像为初始姿态,按照式(11)求得其它帧的相对位姿,实际六自由度的真实值均为零,计算每个自由度与零的差值,取150帧图像差值的平均值,得到每个位置六自由度重复定位的误差。分别计算改进前后标签的重复定位误差,实验结果如图6所示。

图6 小倾角六自由度重复定位误差Fig.6 Small angle six degrees of freedom repeated positioning error

ArUco标签在tx,ty,tz位置上的最大平均误差分别为1.25,2.19,16.32 mm,rx,ry,rz最大平均误差分别为3.89°,2.28°和0.27°,改进标签在tx,ty,tz位置上的最大平均误差分别为0.41,0.44,4.16 mm,rx,ry,rz最大平均误差分别为1.64°,1.47°和0.11°。此外,随着距离的增加,改进前后标签的重复定位误差均呈现出增大的趋势,但ArUco标签的重复定位误差在个别地方出现较大的异常值,重复定位效果不如改进标签。

大倾角实验时,调整标签平面与相机光轴夹角为近似50°,同样测量不同距离下改进前后标签的重复定位误差,实验和数据处理过程与小倾角实验相同,实验结果如图7所示。ArUco标签在tx,ty,tz位置上的最大平均误差分别为36.43,18.84,47.38 mm,rx,ry,rz最大平均误差分别为3.64°,2.11°和1.54°,改进标签在tx,ty,tz位置上的最大平均误差分别为15.21,11.43,17.88 mm,rx,ry,rz最大平均误差分别为1.37°,1.32°和1.01°。与小倾角的重复定位精度相比,ArUco标签在大倾角的重复定位精度明显下降,改进标签在重复定位精度方面更加突出。

图7 大倾角六自由度重复定位误差Fig.7 Large angle six degrees of freedom repeated positioning error

3.2.2 旋转平移精度分析

调整标签平面与相机相距2.5 m并垂直于相机光轴,拍摄10帧图像,以重复测量结果的均值作为初始位姿,此时姿态记为rx=0°,随后用机械臂带动标签绕标签坐标系的x轴旋转10°,共6次至rx=60°,每个位置拍摄10帧图像。计算每个位置上10帧图像相对rx=0°时的rx角度的平均值,rx的真值依次为10°至60°,以平均值与真实值的差值作为误差。同样,将标签绕标签坐标系的y轴和z轴旋转,每次间隔10°拍摄10帧图像,计算ry和rz的误差。分别在3,3.5,4 m处的位置,按照上述方法计算改进前后标签的旋转测量误差,实验结果如图8所示,rx=0°处的误差以其重复定位误差来计算。

图8 不同距离各轴的旋转精度Fig.8 Rotation accuracy of each axis at different distances

图8给出了改进前后标签在不同距离下各轴的旋转误差,可见,在2.5～4 m测量范围内,改进前rx和ry的误差小于4.65°,rz的误差小于1.47°,改进后rx和ry的误差均小于1.78°,rz的误差小于0.8°。

针对沿相机坐标系的x轴的平移精度,实验方案与旋转精度的测量方案类似,同样在2.5 m处调整好标签平面与相机光轴垂直,拍摄10帧图像,此时姿态记为tx=0,以机械臂带动标签在左右方向上平移,间隔50 mm平移1次,各移动至tx=-200 mm与tx=+200 mm。取tx=0处10次测量结果的平均值作为初始位姿,计算每个位置的10帧图像相对初始位置tx=0的相对位姿平均值,然后将平均值与真实值的差值绝对值作为tx的误差。分别在3,3.5,4 m处对改进前后标签的平移误差进行测量,其中3.5 m和4 m处测量范围为tx=-400 mm至tx=+400 mm,测量步长为100 mm。

同样,以机械臂带动标签在上下方向平移,计算ty误差。实验结果如图9所示,在2.5～4 m测量范围内,改进前tx误差小于14.69 mm,改进后tx误差则小于4.86 mm;改进前ty误差小于13.95 mm,改进后ty误差则小于4.52 mm。

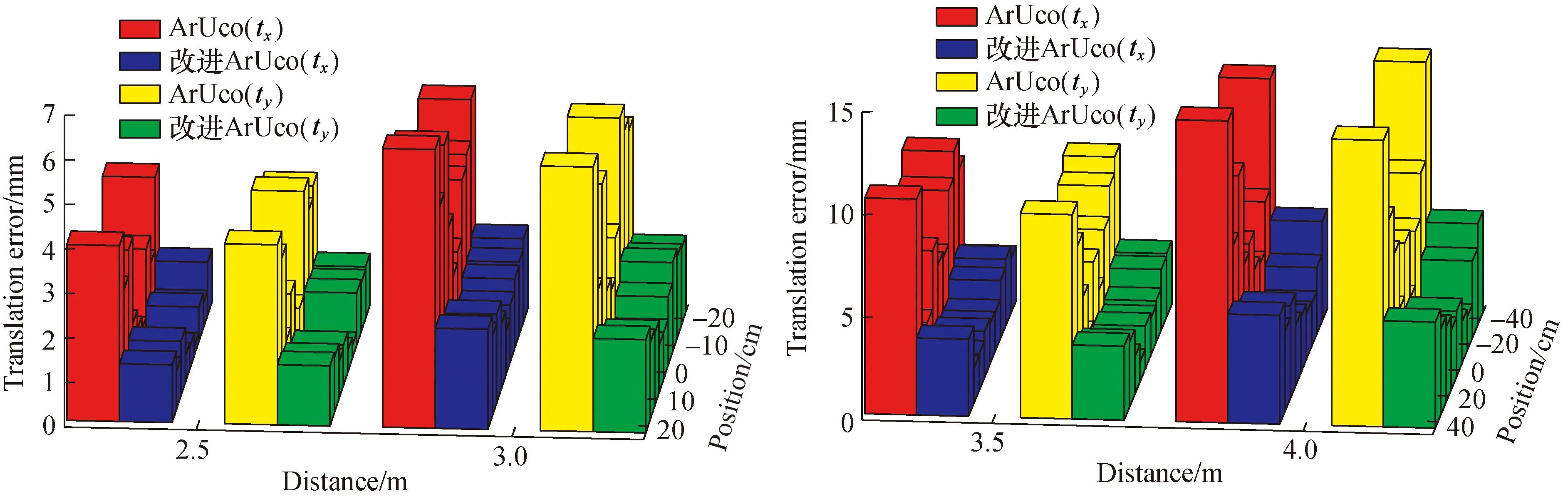
图9 不同距离的平移精度Fig.9 Translation accuracy at different distances

针对沿相机坐标系的z轴的平移精度,同样在2.5 m处拍摄10帧图像,用机械臂带动标签远离相机方向移动至tz=4 m处,测量步长设置为10 cm,真值依次为10,20至150 cm,得到tz误差,实验结果如图10所示。改进前tz误差小于36.32 mm,改进后tz误差小于8.72 mm;且改进标签在4 m处相对测量误差为0.22%,较改进前的相对测量误差降低了0.69%。

图10 沿Z轴的平移精度Fig.10 Translation accuracy along the Z axis

4 结 论

ArUco标签在远距离的位姿估计精度不高,本文在ArUco标签的对角线上增加特征圆环,结合圆心和角点共线的特点,进行直线拟合,对角点像素坐标进行修正。采用EPnP+LM算法对3D-2D点进行位姿解算优化,通过最小化重投影误差求得相机位姿。

2组实验得出以下结论:

1)通过在小倾角和大倾角2种情况对改进前后的标签进行重复性实验,证明改进后的标签的重复定位精度更高。

2)提出的改进ArUco标签在2.5～4 m的距离下进行位姿测量,旋转误差不大于1.78°,平移误差不大于8.72 mm,提高了测量精度。