空间众包中一种支持高效任务分配的隐私保护方案

李惟佳，李军义，龚志茂，谭湘杰

（1.湖南大学 校园信息化建设与管理办公室，湖南 长沙 410082；2.湖南大学 信息科学与工程学院，湖南 长沙 410082）

0 引言

众包[1](Crowdsourcing)是一类新兴的分布式工作模式，是指将原本由机构或个人完成的任务通过互联网公开招募的方式外包给大量未知网络人群的一种行为。作为一种符合国家发展的全新经济模式，众包服务已被广泛应用于现实生活中，《中华人民共和国国民经济和社会发展第十四个五年规划和2035 年远景目标纲要》第十五章也明确指出:“深入推进服务业数字化转型，培育众包设计、智慧物流、新零售等新增长点。”空间众包[2](Spatial Crowdsourcing)是众包与地理位置紧密结合的产物，其中包含3 类实体，分别为任务请求者（以下简称请求者）、任务工作者（以下简称工作者）和云服务器。请求者将任务发布至云服务器，工作者从云服务器上选择任务并物理移动到指定位置来执行任务。

由于工作者不可能时刻关注任务列表，为了保证任务被执行率，云服务器通常会设计一种任务分配方法来自动分配任务。当收到来自请求者的任务后，云服务器按照分配规则将其分配给合适的在线工作者。位置是任务分配过程中的一项重要评估指标，为了保证任务分配的质量，防止出现超出预期的分配误差，云服务器需要周期性地收集在线工作者的实时位置。然而值得注意的是，云服务器并非完全可信的实体，一方面，它可以提供正确的服务；另一方面，它可能会在未经授权的情况下非法访问用户的敏感数据，并推测出个人隐私。例如，云服务器可以利用工作者的连续位置数据绘制轨迹图来分析行为规律，也可以利用任务位置来推测请求者的家庭住址、工作单位等敏感信息[3-4]。特别是当位置与医疗服务相关时，恶意的服务提供者可能会利用这一信息不公正地决定是否接收其保险和劳务合同[5]。

为了解决这一问题，近年来研究者们提出了几种基于位置的可搜索加密方案[6-10]保护参与者的位置数据安全。用户先在本地加密位置信息然后仅将密文上传至云服务器，云服务器会在密文上进行任务分配。然而，这些方案无法保证任务分配的高效性，因为加密在保护数据隐私的同时会带来额外的计算开销。一些方案仅支持线性时间复杂度的任务分配服务，单次任务分配的时间开销需要十几分钟甚至几个小时；另外一些方案针对效率问题进行了改进，支持了次线性时间复杂度的任务分配服务，然而这些方案的时间开销不具备稳定性，整体开销会随在线工作者数量的增加而增加，无法满足当前大数据时代的需求。

针对这一挑战，本文提出了一种基于索引树的可搜索加密方案，在保护参与者双向位置隐私安全的同时支持高效且稳定的任务分配服务。具体而言，本文采用一种递归分解算法将众包区域划分为若干网格并为每个网格生成唯一二元标识向量，然后提出了一种自下而上的索引树构建算法来生成一棵网格索引四叉树。为了保护参与者的位置隐私安全，本文使用一种对称隐藏向量加密算法SHVE(Symmetric-key Hidden Vector Encryption)[11]。实验分析展示了本文方案各方面的性能表现，与现有工作相比，本文所提出的方案在任务分配方面的性能表现更优。尤其是当索引树高度固定时，本文方案在任务分配方面的时间开销是稳定的，不受在线工作者数量影响。

1 相关知识

1.1 系统模型

本文方案的系统模型如图1 所示，其中包含4 类实体：授权中心、请求者、工作者和云服务器。授权中心是一个完全可信的第三方实体，负责生成系统密钥和索引树，并管理用户的注册和注销。请求者向云服务器发起众包任务，服务器则按照预先约定的规则将任务分配给合适的工作者。最后，接受任务的工作者需要物理移动到任务所指定的位置来完成任务。

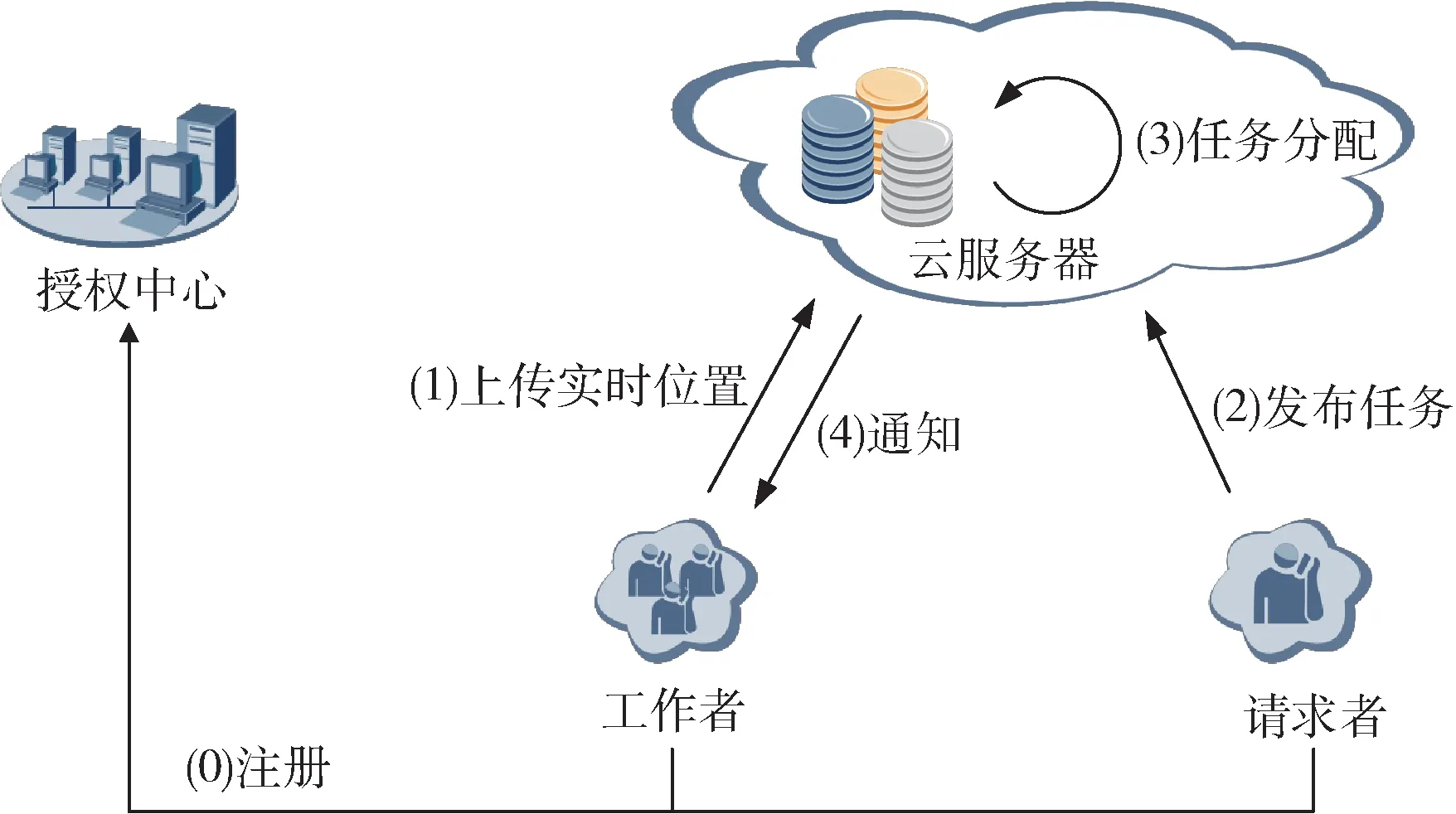
图1 系统模型

1.2 威胁模型

本文假定云服务器是一类“诚实但好奇”的实体，这一假设被广泛应用于现有的隐私保护工作中[12-14]。具体而言，一方面云服务器被认为是诚实的，能够提供正确的服务且不会恶意地修改数据；另一方面，云服务器是好奇的，渴望收集更多的额外信息来获取更高的利益。

1.3 对称向量隐藏加密算法

SHVE 是一种支持在密文上进行合取的对称向量隐藏加密算法。定义F0表示一个伪随机函数，E0表示一种支持加密计算Enc 和解密计算Dec 的对称加密算法，Γ表示一个有限属性集合{0,1}，*表示不存在于Γ中的通配符，Γ*表示Γ∪{*}，SHVE 算法可描述为如下4 部分：

如果μ=0λ+logλ，系统输出True，表示密文与陷门匹配成功；否则输出⊥，表示无法正确执行。

2 方案描述

本文设计了一种网格索引四叉树结构来实现高效且稳定的任务分配效率，并采用SHVE 加密算法来保护索引树及参与者的隐私安全。系统初始化阶段，授权中心选择安全参数λ并执行SHVE.Setup(1λ) 来生成主密钥msk。

2.1 网格索引四叉树构建

利用网格思想将原本复杂的坐标距离计算转换为更为简单的网格比较是空间众包隐私保护研究中的常用方法之一。对于大小为T×T的空间区域，可将其划分为若干大小相等的网格，并将同一网格内的所有位置坐标归一到网格中心坐标。换句话说，如果两个用户位于同一网格，则他们被认为处于同一位置。

本文采用一种递归分解算法来进行网格划分并为每个网格生成唯一的二元标识向量。递归分解的过程如下：

(1) 对经度进行二分，得到左右两个子区间；

(2) 对纬度进行二分，得到上下两个子区间；

(3) 对得到的4 个子区域按照左上、左下、右上、右下的顺序分别编码为00、01、10、11；

(4) 如果精度未达到要求，将上面得到的4 个子区域分别作为输入重复上述操作。

假设预期精度为ρ，区域最终被分解为22ρ个网格，每个网格对应一个2ρ位长的二元标识向量。ρ=2 时的递归分解过程如图2(a)所示。区域首先被分解为4 个部分，然后每个子区域再进行递归分解。图中给出了左上子区域的第二轮递归示例，其他区域同理，每个网格的向量由父区域编码与子区域编码拼接而成，例如0001 由00 与01 拼接而成。

图2 ρ=2 时建立网格索引四叉树的流程

网格划分完成之后，本文设计了一种自下而上的构建算法来创建一棵网格索引四叉树。在描述索引树构建流程之前给出向量计算符∧的定义：对于任意两个m比特的向量v,w∈，如果存在一个向量p∈满足

其中，1≤l≤m，则有v∧w=p。例如，向量1001 和1000 仅在第四个比特值不同，因此可以计算得到1001∧1000=100*。

索引树的构建过程可视为网格递归分解的逆向过程，首先为所有网格建立节点作为叶子节点，然后向上逐层建立中间节点直至所有的节点汇聚为根节点。构建索引树的过程如下：

(1) 为所有网格创建对应的叶子节点，并将网格的二元向量记为节点的标识向量，特别地，每个叶子节点维护一个工作者队列Q用于记录可用工作者信息；

(2) 记(N0,N1,N2,N3)为处于同一子区域的4 个节点，Ni.g(0≤i≤3)表示节点的标识向量，将这4 个节点作为子节点向上建立父节点，父节点的标识向量计算为N0.g∧N1.g∧N2.g∧N3.g；

(3) 将上一步的结果作为输入，重复步骤(2)直至输出结果为根节点。

执行上述过程，最终将生成一棵高度为ρ+1 的网格索引四叉树。ρ=2 时生成的索引树如图2(b)所示。以图2(a)的左上区域为例，首先创建4 个叶子节点并记录对应的二元向量为节点标识向量，然后向上建立父节点，并计算父节点的标识向量为: (0000∧0001)∧(0010∧0011)=000*∧001*=00**。

其他节点的处理过程类似。此外，为了保护参与者的位置隐私安全，防止云服务器通过索引树推测出用户的真实位置信息，授权中心需要对索引树的所有节点执行SHVE.Gen 计算，将节点的标识向量替换为陷门。最后，授权中心将索引树发送给云服务器用于后续的任务分配服务。

2.2 位置上传请求

工作者向授权中心注册以获取密钥。为了防止隐私泄露，每一轮位置上传过程中，工作者先在本地加密位置信息，然后提交密文数据至云服务器。假设工作者本轮需要上传的地理坐标为(xw,yw)，首先将地理坐标转换为所在网格的二元标识向量gw，然后执行SHVE.Enc(gw,msk)得到，最后将上传至云服务器。

2.3 任务分配请求

类似地，请求者也需要先向授权中心注册以获取密钥。假设请求者发起任务的地理坐标为(xt,yt)，首先将地理坐标转换为所在网格的向量标识符gt，然后执行SHVE.Enc(gt,msk)得到，最后将和任务内容发送至云服务器。

最后，云服务器最终将任务内容下发给候选工作者，工作者可以选择接受或者拒绝任务。如果没有工作者接受任务，云服务器将任务挂起并在下一轮分配流程中重新计算。

3 实验分析

3.1 实验环境描述

本文方案通过Python3 实现，其中SHVE 算法的安全参数λ=128，E0选为AES 算法，运行环境为Ubuntu 22.04，2 Intel(R) Xeon(R) Silver 4110 CPU @ 2.10 GHz,128 GB RAM。

本文实验数据取自于真实数据集Gowalla，其中包含来自196 591 名用户的6 442 890 条带有位置坐标的打卡记录。本文从Gowalla 数据集中选取纬度在(30.26,30.27)，经度在(-97.75,-97.74)区间内的共51 959 条数据作为测试数据集。为了避免实验结果的偶然性，实验结果皆为多次实验的平均值。本文还将方案ETA[7]、Priradar[8]、GPSC[9]和PPTA[10]用于对比。ETA 是一种基于Paillier[15]的安全准确任务分配协议；Priradar 是一种基于变色龙哈希的位置隐私保护框架；GPSC 是一种基于Bloom 过滤器[16]的网格隐私保护方案；PPTA 是一种同时支持在线任务分配和批量任务分配的灵活的位置隐私保护方案，公平起见，下文对比实验中的数据仅记录其在线任务分配设置下的性能表现。

3.2 理论分析

本节使用到的符号及其相应的含义如表1 所示，指定参数ρ，本文方案将生成一棵高度为ρ+1 的索引树，其中每个节点的标识向量长度为2ρ，此时单次SHVE.Gen、SHVE.Enc 和SHVE.Query 计算的时间开销分别为2ρ(Tp+Txor)+Tenc、2ρTp和2ρTxor+Tdec。本节将分别对索引树构建、位置上传和任务分配进行理论分析。

表1 理论分析符号表

(1) 索引树中任意节点的生成包括一次标识向量计算和一次SHVE.Gen 计算，前者的时间开销为Tg，后者的时间开销为2ρ(Tp+Txor)+Tenc。一棵高度为ρ+1 的索引树的总节点数量为(4ρ+1-1)/3，因此，构建索引树的总时间开销为(2ρ(Tp+Txor)+Tenc+Tg)(4ρ+1-1)/3。

(2) 工作者位置上传流程包括一次SHVE.Enc 计算和一次深度优先检索，前者的时间开销为2ρTp，后者则需要进行O(ρ+1)次节点检索。对于每个检索节点，需要执行一次SHVE.Query 计算，整个检索过程的时间开销可表示为O(ρ+1) (2ρTxor+Tdec)。因此，工作者位置上传流程的总时间开销为2ρTp+O(ρ+1) (2ρTxor+Tdec)。

(3) 请求者任务分配流程包括一次SHVE.Enc 计算、一次深度优先检索和一次任务分配计算，其中前两个部分的整体时间开销为2ρTp+O(ρ+1) (2ρTxor+Tdec)。任务分配也可视为一次节点检索流程，时间开销与所访问的节点数量相关，记为O(n)。因此，请求者任务分配流程的总时间开销为2ρTp+O(ρ+1)(2ρTxor+Tdec)+O(n)。

3.3 实验结果分析

本节对实验结果进行分析，首先分析了参数ρ对单位网格粒度的影响，然后展示了索引树建立、位置上传及任务分配3 方面的性能表现。

不同参数ρ下单位网格面积的演变趋势如图3 所示。理论上，ρ越大，划分网格数量越多，单位网格面积越小，粒度越细。本文设置ρ=11 为本节实验的最大边界值。在该参数下，数据集的覆盖区域将被划分为 4×106个网格，单位网格面积约为0.255 m2，该粒度能够满足大部分现实应用的精度需求。

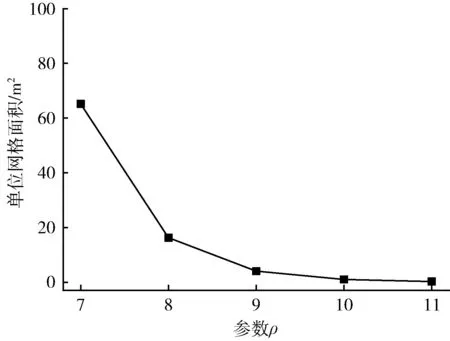
图3 不同ρ 下的单位网格面积

不同粒度下构建一棵网格四叉索引树的时间开销如图4 所示。理论分析中指出，构建索引树的时间开销仅与ρ正向相关。粒度越小，ρ越大，建索引树的理论时间开销也越大，图中的曲线变化趋势也反映了这一结论。从实验结果来看，构建一棵细粒度的索引树的时间开销是不容忽视的。然而，索引树只需要在系统初始化阶段构建一次，即使后续需要更改，授权中心也可以预先计算。因此，在实际生产中，该部分的时间成本是可以接受的。

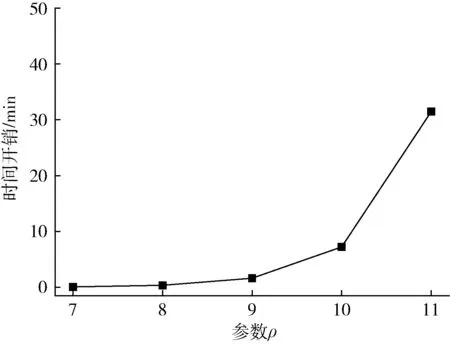
图4 不同网格粒度下构建索引树的时间开销

不同参数ρ下位置上传请求的时间开销如图5 所示。位置上传请求的时间成本主要来源于两个部分：工作者本地加密和索引树深度优先搜索计算。加密部分的时间开销受加密算法和密钥复杂度的影响，该部分时间开销视为恒定的，因为这些配置在系统初始化阶段被选定且不会改变。而深度优先搜索的时间开销则可表示为O(ρ+1)，其中ρ+1 表示为索引树高度。这意味着位置上传请求的时间开销将与ρ正向相关，这与图中曲线趋势一致。值得注意的是，当ρ=11 时，位置上传请求的执行时间仅约为1.34 ms，该延时在实际应用中往往是难以察觉的，这也意味着即使在高粒度的网格划分中本文方案依然能够支持高效的位置上传请求。

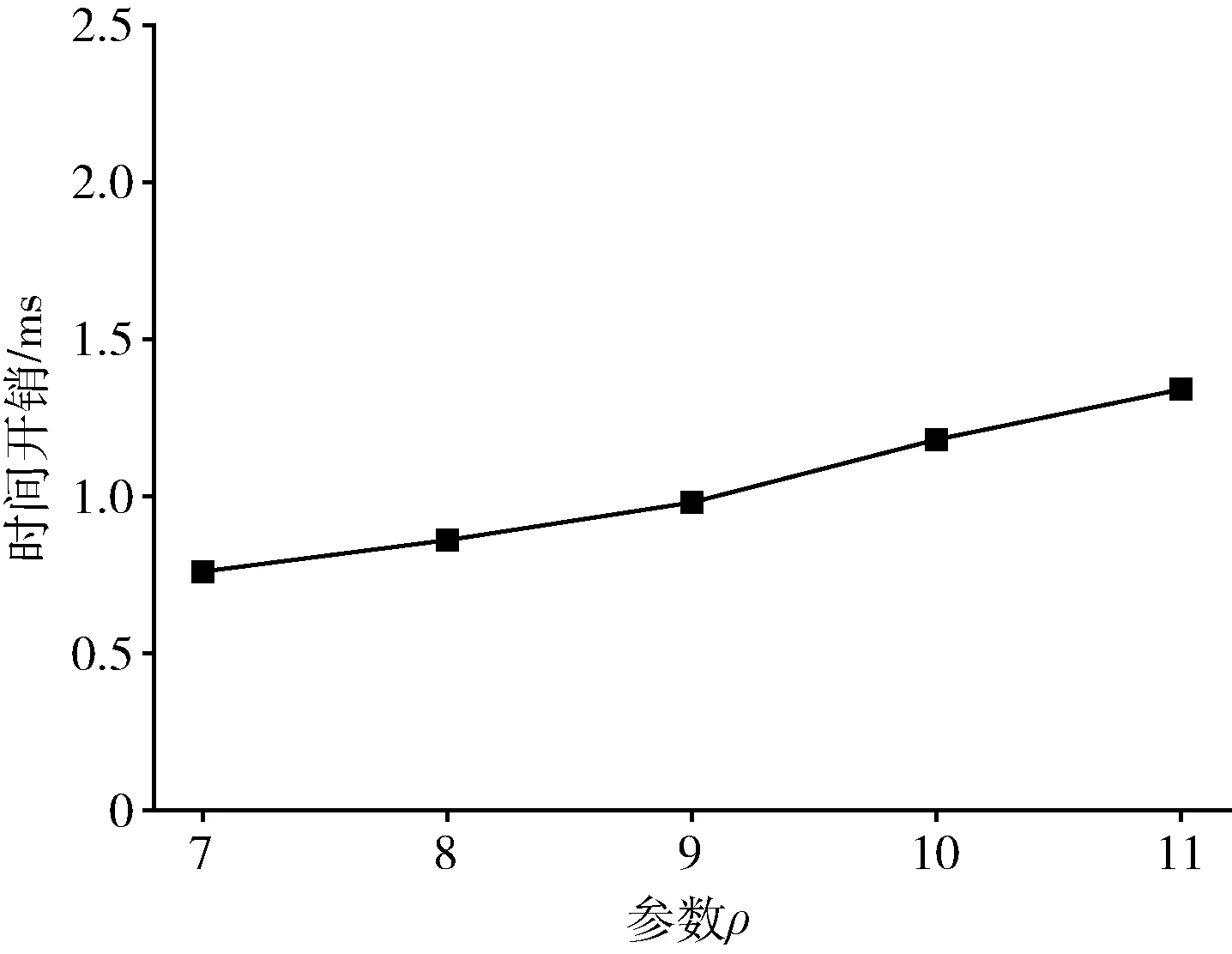
图5 不同ρ 下的位置上传的时间开销

不同参数ρ下任务分配请求时间开销如图6 所示，其中工作者数量固定为10 000，任务位置固定为区域中心坐标。任务分配请求的时间成本主要来源于3 个部分：请求者本地加密、索引树深度优先搜索和任务分配。正如上面所分析的，本地加密部分的时间开销是恒定的，深度优先搜索部分的时间开销与ρ正向相关。任务分配部分的时间开销取决于检索节点数量。但是，由于该部分不涉及密文计算，其时间开销是可以忽略的。因此，图中的时间曲线与图5 相似，且同样维持在毫秒级别。为了展示本文方案在任务分配方面的性能表现，本文设置ρ=11 并将工作者的数量从2 000 增加到10 000，然后随机选择1 000 个坐标作为任务位置，最后的平均时间开销记录如表2 所示。从实验结果可知，本文所提出的方案在性能表现上优于现有的所有方案，能够在毫秒级别处理单个任务分配请求。此外，不同于现有工作，当索引树的高度固定时，本文方案在任务分配方面的时间开销还具有稳定性。这是因为本文方案在任务分配方面的时间开销主要集中在本地加密和深度搜索计算方面，而这两部分的时间开销仅与ρ正向相关，与在线工作者数量无关。

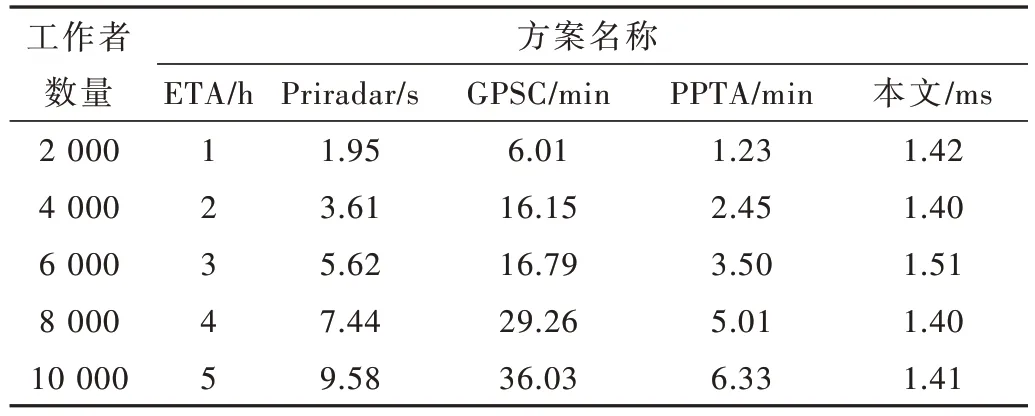
表2 方案对比

图6 不同ρ 下的任务分配的时间开销

定义密文下的实际分配距离为dc，明文下的理论最优分配距离为dp，任务分配的相对距离误差可以表示为e=|dc-dp|。一般而言，相对距离误差越小，任务分配质量越高。不同参数ρ下的任务分配请求的相对距离误差如图7 所示。2.1 小节指出位于同一网格内的工作者将被视为位于网格中心坐标，即他们分配任务的概率是均等的。理论上，工作者的真实坐标与网格中心坐标之间存在一定的偏差，且单位网格面积越小，偏差范围越小。图3 指出，ρ越大时单位网格面积越小，即ρ越大，偏差范围越小，此时的相对距离误差也就越小，任务分配质量也就越高。图中曲线证实了这一理论。

图7 不同ρ 下的任务分配的相对距离误差

4 结论

随着移动设备和无线互联网的发展，空间众包服务近些年得到了大力发展，同时也暴露了一些安全问题。本文关注于空间众包服务中的位置隐私泄露问题，提出了一种支持高效任务分配的可搜索加密方案来保护参与者的位置信息免受半诚实的云服务器的侵犯。具体而言，本文首先提出了一种基于网格的索引四叉树结构来保证任务分配计算的高效性，然后采用了一种对称隐藏加密算法来保障参与者及索引树的安全性。大量基于真实数据集的实验表明，本文方案在大规模工作者数量场景中的任务分配性能表现优于现有其他工作。