基于HyperLynx的电信号串扰仿真分析

王强 王杨 赵目龙 娄立新 王祎帆

【摘要】在高速数字电路中，电信号串扰是影响信号完整性的一个主要因素。针对近端电信号串扰噪声和远端电信号串扰噪声进行理论建模，借助信号完整性仿真工具HyperLynx进行仿真分析，研究攻击线与受害线的间距、耦合长度、信号线到参考平面的介质层厚度、信号上升沿及下降沿速率对于电信号串扰的影响。仿真结果表明：合理的设计可以有效抑制电信号串扰，进而提高电路信号完整性。

关键词：高速电路；HyperLynx；信号完整性；电信号串扰；仿真；

中图分类号：U464.12+3   文献标志码：A  DOI： 10.19822/j.cnki.1671-6329.20220255

Simulation Analysis of Electrical Signal Crosstalk Based on HyperLynx

Wang Qiang， Wang Yang， Zhao Mulong， Lou Lixin， Wang Yifan

（Global R&D Center， China FAW Corporation Limited， Changchun 130013）

【Abstract】 In high-speed digital circuits， electrical signal crosstalk is one of the main factors affecting signal integrity. The theoretical model of the near end electrical signal crosstalk noise and the far end electrical signal crosstalk noise is established in this paper， and some parameters affecting electrical signal crosstalk are simulated by using the signal integrity simulation tool HyperLynx， such as the distance between aggressor line and victim line， the coupling length， the thickness of dielectric layer from the signal line to reference plane and the rates of rising as well as falling edges of signals. The simulation results show that the reasonable design can effectively suppress the electrical signal crosstalk and improve the signal integrity of the circuit.

Key words： High-speed circuit， HyperLynx， Signal integrity， Electrical signal Crosstalk， Simulation

缩略语

EMMC    Embedded Multi Media Card

DDR4    Double Data Rate 4th-generation Synchronous

Dynamic Random-access Memory

PCB      Printed Circuit Board

IFC      Intelligent Front Camera

SOC    System on Chip

IBIS    Input/Output Buffer Information

Specification

NEXT  Near End Crosstalk

FEXT  Far End Crosstalk

0 引言

隨着自动驾驶、智能座舱技术的快速发展，嵌入式多媒体卡（Embedded Multi Media Card，EMMC）、双倍数据速率第4代同步动态随机存取内存（Double Data Rate 4th-generation Synchronous Dynamic Random-access Memory，DDR4）等高速存储芯片在汽车上得到了大规模应用。传统汽车电子控制器通常处理的是一些低频、大功率信号，例如发动机控制器中喷油和点火信号。在传统印刷电路板（Printed Circuit Board，PCB）设计中主要考虑信号通流能力、散热因素。智能网联汽车电子控制器中包含有大量的高速信号，例如智能前视摄像头（Intelligent Front Camera，IFC）控制器中系统芯片（System On Chip，SOC）与DDR4的数据交互信号，通讯速率可以达到2 666 Mbit/s。在此类控制器的PCB设计过程中，必须考虑信号完整性的问题，否则控制器可能无法正常工作。

伴随着PCB尺寸缩小和信号通讯速率不断提升，电信号串扰对于电路可靠性影响愈发严重[1-4]。电信号串扰是影响信号完整性的一个重要因素。

本文针对于近端电信号串扰和远端电信号串扰进行理论建模分析。在此基础之上，通过仿真工具HyperLynx对攻击线与受害线之间的间距、耦合长度、信号线到参考平面介质层厚度、信号上升沿和下降沿速率进行详细仿真分析，研究上述参数对于电信号串扰的影响。

1 电信号串扰形成机理

信号在传输线中传递时，会在其周围产生相应的电场和磁场[5-11]。电信号串扰指的是能量从一根传输线通过寄生电容和寄生电感耦合到另外一根相邻传输线的现象。其中，寄生电容产生的耦合称为容性耦合，寄生电感产生的耦合称之为感性耦合[12-14]。

1.1 容性耦合

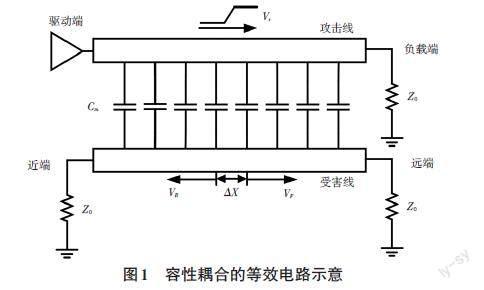
图1为容性耦合的等效电路示意图。假设攻击线和受害线都为均匀传输线，且两根传输线的寄生电容与寄生电感均匀分布在整段传输线上。攻击线上的信号为上升沿信号，稳定电压为VS。攻击线驱动端输出阻抗为0，攻击线负载端阻抗为Z0。受害线驱动端和负载端都进行端接，且端接阻抗为Z0。Cm为两根传输线单位长度的互容。

针对于受害线上一小段传输线ΔX，由基尔霍夫电流定律可得：

[VBCZ0+VFCZ0=Cm×ΔX×dVSdt]               （1）

式中：VBC为受害线上传向近端的容性耦合电压，VFC为受害线上传向远端的容性耦合电压。

由于受害线上的阻抗处处相等，且寄生电容感生出来的电流，一半流向近端，一半流向远端。那么，可得：

[VBC=VFC=12×Cm×ΔX×dVSdt]              （2）

若信号上升沿为线性的，且两根传输线的耦合长度一定，那么由式（2）可得近端容性耦合电信号串扰为：

[VNEXTC=12×12×Cm×υ×Tr×VSTr]             （3）

式中：υ为攻击线上信号的传播速度，Tr为攻击线上信号上升沿时间。

式（3）可以简化为：

[VNEXTC=14×Cm×υ×VS]                    （4）

由式（2）可得远端容性耦合电信号串扰为：

[VFEXTC=12×Cm×LT×VSTr]                    （5）

式中：LT为两根传输线的耦合长度。

针对于近端容性耦合电信号串扰，当攻击线上有上升沿信号出现时，受害线上的感生电流会以一个恒定的速度向近端移动。当两根传输线的耦合长度小于饱和长度时，近端容性耦合的电压值会随着耦合长度的增加而变大。其中，饱和长度Lensat为：

[Lensat=υ×Tr]                               （6）

当两根传输线的耦合长度大于饱和长度时，近端容性耦合电压值会达到一个稳定值，不再继续增加。当变化的信号达到攻击线的负载端时，受害线上不再有新的感生电流产生，但还会有电流传向受害线的近端，且持续时间为TD，其中TD为攻击线上变化的上升沿信号从驱动端到负载端的传输延迟。受害线上的近端容性耦合电压变化曲线如图2所示。

针对于远端容性电信号串扰，当攻击线上的上升沿信号到达负载端时，才会在受害线的远端产生电信号串扰电压噪声，且该噪声的持续时间等于攻击线上信号的上升沿时间Tr。受害线上的远端容性耦合电压变化曲线如图3所示。

综上所述，针对于近端容性耦合电信号串扰而言，其会在受害线的近端产生一个宽信号，且信号的宽度会随着耦合长度的增加而增加。针对于远端容性耦合电信号串扰而言，会在受害线的远端产生一个窄脉冲信号，且信号的幅值会随耦合长度的增加而增加。

1.2 感性耦合

图4为感性耦合的等效电路示意图，其中攻击线上的电流为IS，Lm为两根传输线单位长度的互感。

针对于受害线上的一小段传输线ΔX，由基尔霍夫电压定律可得：

[VBL=Lm×ΔX×dISdt+VFL]                   （7）

式中：VBL为受害线上传向近端的感性耦合电压，VFL为受害线上传向远端的感性耦合电压。

其中：

[VBLZ0=-VFLZ0]                               （8）

[IS=VSZ0]                                 （9）

將式（8）和式（9）带入式（7）中可得：

[VBL=12×LmZ0×ΔX×dVSdt]                 （10）

[VFL=-12×LmZ0×ΔX×dVSdt]                （11）

若信号上升沿为线性，且两根传输线的耦合长度一定，那么由式（10）可得近端感性耦合电信号串扰为：

[VNEXTL=14×LmZ0×υ×VS]                  （12）

远端感性耦合电信号串扰为：

[VFEXTL=-12×LmZ0×LT×VSTr]                 （13）

针对于近端感性耦合电信号串扰，其与近端容性耦合电信号串扰近似。当两根传输线的耦合长度小于饱和长度时，近端感性耦合的电压值会随着耦合长度的增加而变大。当两根传输线的耦合长度大于饱和长度时，近端感性耦合电压值会达到一个稳定值。受害线上的近端容性耦合电压变化曲线如图5所示。

针对于远端感性电信号串扰，当攻击线上的上升沿信号到达负载端时，才会在受害线的远端产生电信号串扰电压噪声，且该噪声的持续时间等于攻击线上信号的上升沿时间Tr。但远端感性电信号串扰和远端容性电信号串扰的耦合电压方向相反。受害线上的远端感性耦合电压变化曲线如图6所示。

综上所述，针对于近端感性耦合电信号串扰而言，其会在受害线的近端产生一个宽信号，且信号的宽度会随着耦合长度的增加而增加。针对于远端感性耦合电信号串扰而言，其会在受害线的远端产生一个窄脉冲信号，且信号的幅值会随耦合长度的增加而增加。

1.3 近端电信号串扰

针对于近端电信号串扰而言，容性电信号串扰和感性电信号串扰同时存在。由1.1和1.2小节可得：

[VNEXT=VNEXTC+VNEXTL]                    （14）

将式（4）和式（12）带入式（14）中：

[VNEXT=14×Cm×υ×VS+14×LmZ0×υ×VS]      （15）

由传输线的基本理论可知：

[υ=1L0×C0]                          （16）

[Z0=L0C0]                              （17）

将式（16）和式（17）帶入式（15）中可得：

[VNEXT=14×VS×CmC0+LmL0]                （18）

从式（18）中可以得知，近端电信号串扰的幅值与传输线间互感和互容强相关。

1.4 远端电信号串扰

针对于远端电信号串扰而言，容性电信号串扰和感性电信号串扰也同时存在。由1.1和1.2小节可得：

[VFEXT=VFEXTC+VFEXTL]                    （19）

将式（5）和式（13）带入式（19）中：

[VFEXT=12×Cm×LT×VSTr-12×LmZ0×LT×VSTr]   （20）

将式（16）和式（17）带入式（20）中可得：

[VFEXT=12×TD×VSTr×CmC0-LmL0]          （21）

式中：TD为信号在攻击线上的传输延迟。

从式（21）中可以得知，当Cm/C0等于Lm/L0时，远端容性电信号串扰与远端感性电信号串扰互相抵消。此外，远端电信号串扰的幅值与信号在攻击线上的传输延迟TD和攻击线上信号上升沿时间强相关。

2 电信号串扰仿真分析

将针对攻击线与受害线的间距、耦合长度、信号线到参考平面的介质层厚度、信号上升沿和下降沿的速率参数进行仿真分析。仿真工具为Mentor Graphics旗下的信号完整性仿真工具HyperLynx，软件版本为VX.2.6。

图7为电信号串扰仿真在HyperLynx软件中的示意图，其中U1.1为攻击线的输出缓冲器，TL1为攻击线的传输线，R1为攻击线的负载电阻，TL2为受害线的传输线，R2为受害线的源端电阻，R3为受害线的负载电阻。仿真中，R1=63.0 Ω、R2=63.0 Ω、R3=63.0 Ω。

2.1 攻击线与受害线间距

仿真中，将TL1和TL2线设定为宽度为0.15 mm的顶层走线，两根传输线的耦合长度TC为76.20 mm，线与线的间距TS从0.15 mm拉大到0.30 mm，每次仿真间距步长为0.05 mm。

从图8中可以看到，随着两根传输线间距的增大，近端电信号串扰的峰值在逐步下降。当两根传输线的间距为0.15 mm时，近端电信号串扰的峰值为191.20 mV。当两根传输线的间距为0.30 mm时，近端电信号串扰的峰值为81.50 mV。通常，两根传输线的互感和互容会随着传输线间距的减小而变大。上述近端电信号串扰的电压变化趋势与式（18）理论分析一致。

从图9中可知，随着传输线间距的增大，远端电信号串扰的峰值逐渐减小。当两根传输线的间距为0.15 mm时，远端电信号串扰的峰值为-69.04 mV。当两根传输线的间距为0.30 mm时，远端电信号串扰的峰值为-92.37 mV。

2.2 耦合长度

仿真中，将TL1和TL2线设定为宽度为0.15 mm的顶层走线，两根传输线边与边的间距为0.20 mm，耦合长度从25.40 mm增大到152.40 mm，每次仿真耦合长度的步长为25.40 mm。

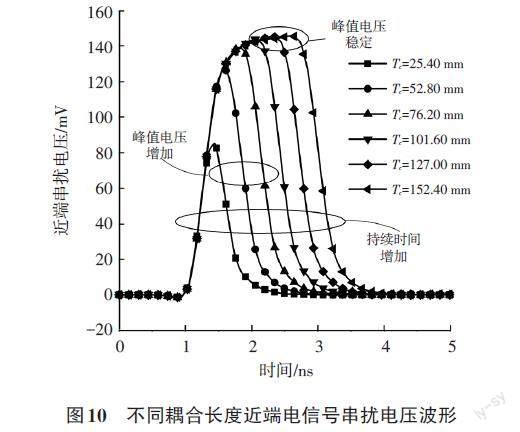
图10为不同耦合长度下的近端电信号串扰电压波形。从图10中可以看到，当两根传输线的耦合长度在25.40～76.20 mm之间时，随着耦合长度的增加，近端电信号串扰电压的峰值逐渐增加。此时，传输线的耦合长度小于饱和长度。当两根传输线的耦合长度在101.60～152.40 mm之间时，近端电信号串扰电压的峰值不再变化，达到一个稳定数值。此时，传输线的耦合长度大于饱和长度。此外，随着两根传输线耦合长度的增加，近端电信号串扰噪声的持续时间也随之增加。

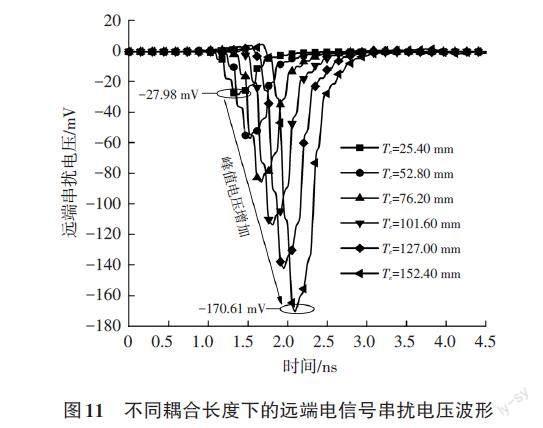
图11为不同耦合长度下的远端电信号串扰电压波形。从图11中可以看到，随着两根传输线耦合长度的增加，远端电信号串扰的峰值电压从-27.98 mV增加到-170.61 mV。但远端电信号串扰噪声的持续时间并不会随着耦合长度的增加而增加。

2.3 信号上升沿和下降沿速率

仿真中，将TL1和TL2线设定为宽度为0.15 mm的顶层走线，两根传输线边与边的间距为0.20 mm，耦合长度为76.20 mm。设定驱动端的信号为上升沿信号。

通过查看驱动端U1.1的输入/输出缓冲器信息规范（Input/Output Buffer Information Specification，IBIS）模型，可得当信号上升沿速率为典型值（Typical）时，在0.34 ns内电压变化为1.53 V，电压变化率为4.50 V/ns；当信号上升沿速率为快速（Fast）时，在0.26 ns内电压变化为1.75 V，电压变化率为6.72 V/ns；当信号上升沿速率为慢速（Slow）时，在0.53 ns内电压变化为1.25 V，电压变化率为2.36 V/ns。

从图12中可得，随着驱动端信号上升沿的变缓，近端电信号串扰和远端电信号串扰噪声的峰值也随之下降。当信号上升沿速率为Fast时，近端电信号串扰的电压峰值为161.51 mV，远端电信号串扰的电压峰值为-123.53 mV。从式（21）可知，远端电信号串扰的电压峰值与信号上升沿/下降沿的时间成反比，即上升沿和下降沿时间越短，远端电信号串扰的电压峰值越大，仿真结果与理论公式推导一致。

2.4 信号线到参考平面的厚度

仿真中，将TL1和TL2设定为顶层走线，两根传输线边与边的间距为0.20 mm，耦合长度为76.20 mm。信号线到参考平面的介质层厚度Tt分别为0.07 mm、0.10 mm和0.12 mm。为保证传输线的阻抗为63 Ω，在上述介质层厚度的情况下，走线宽度分别为0.08 mm、0.12 mm和0.15 mm。

从图13中可以看出，随着信号线到参考平面介质层厚度的增加，电信号串扰噪聲的峰值也随之增加。图14为不同介质层厚度下的电力线和磁力线分布图。当介质层厚度Tt为0.07 mm时，电信号串扰噪声峰值最小，此时，近端电信号串扰的噪声峰值为77.69 mV，远端电信号串扰的噪声峰值为-62.10 mV，信号线与参考平面间电力线分布较为密集，信号线与信号线间的电力线分布较为稀疏，表征信号线与参考平面间的耦合较强，信号线与信号线间的耦合较弱。当介质层厚度Tt为0.12 mm时，电信号串扰噪声峰值最大，此时，近端电信号串扰的噪声峰值为138.77 mV，远端电信号串扰的噪声峰值为-85.45 mV，信号线与参考平面间电力线分布较为稀疏，信号线与信号线间的电力线分布较为密集，表征信号线与参考平面间的耦合较弱，信号线与信号线间的耦合较强。

3 结束语

抑制电信号串扰是保证信号完整性的一个重要手段。本文对两根传输线间的近端电信号串扰和远端电信号串扰进行详细的理论建模，并通过信号完整性软件HyperLynx进行仿真分析。仿真结果表明，攻击线与受害线间距、耦合长度、信号上升沿和下降沿速率、信号线到参考平面的厚度都会对电信号串扰噪声产生影响。在实际PCB设计中，应通过合理的叠层设计、走线来抑制电信号串扰，从而提高控制器可靠性。此外，高速电路工程师可以通过仿真来确定走线的约束条件，进而提高PCB设计效率和一次打板成功率。

参 考 文 献

[1] 李成， 程晓宇， 毕笃彦， 等. 基于HyperLynx的高速DSP系统信号完整性仿真研究[J].电子器件， 2009， 32（2）： 445-451.

[2] 杨华， 陈少昌， 朱凤波. 高速数字电路PCB中串扰问题的研究与仿真[J]. 电光与控制， 2012（3）： 94-98.

[3] 袁为群， 宋建远， 陈世荣. 基于信号完整性的高速PCB优化设计与研究[J]. 广东工业大学学报， 2019（6）： 74-79.

[4] 张健. 高速数字电路中串扰计算的简化公式[J]. 南京工程学院学报： 自然科学版， 2008， 6（1）： 21-26.

[5] 付兆静. 基于HyperLynx的PCB板信号完整性分析[D]. 哈尔滨： 哈尔滨工程大学.

[6] 李轶敏. 高速电路的信号完整性分析[D]. 南京： 南京航空航天大学， 2008.

[7] 李千. 高速PCB设计中串扰与反射的研究[D]. 哈尔滨： 哈尔滨工程大学， 2016.

[8] 朱亚地. 高速PCB信号反射及串扰仿真分析[D]. 西安： 西安电子科技大学， 2012.

[9] EAKHWAN S， JEONGH. A Wide-Band Passive Equalizer Design on PCB Based on Near-End Crosstalk and Reflections for 12.5 Gbps Serial Data Transmission[J]. Microwave and Wireless Components Letters， 2008， 18（12）： 794-796.

[10] SONG E， CHO J， KIM J， et al. Modeling and Design Optimization of a Wideband Passive Equalizer on PCB Based on Near-End Crosstalk and Reflections for High-Speed Serial Data Transmission[J]. IEEE Transactions on Electromagnetic Compatibility， 2010， 52（2）： 410-420.

[11] 王祎帆， 王杨， 王强， 等. 基于HyperLynx的高速电路端接技术仿真研究[J]. 汽车文摘， 2020（5）： 53-58.

[12] GREEN L. Understanding the Importance of Signal Integrity[J]. Circuits & Devices Magazine IEEE， 1999， 15（6）： 7-10.

[13] GOYAL R. Managing Signal Integrity [PCB design][J]. IEEE Spectrum， 1994， 31（3）： 54-58.

[14] NOVAKI. Modeling， Simulation， and Measurement Considerations of High-speed Digital Buses[J]. IEEE Transactions on Instrumentation and Measurement， 1992， 41（6）： 147-151.

（责任编辑 梵铃）

【作者简介】

王祎帆（—），中国第一汽车股份有限公司研发总院，工程师，研究方向为高速电路设计及SI/PI仿真。

E-mail：wangyifan@faw.com.cn