一种基于地理实体数据自动派生斜坡符号方法
杨健男,殷 勇,郭沛沛, 燕雨晗
(中国测绘科学研究院 地理信息与地图研究所, 北京 100036)
斜坡符号是地形图中常见的一种地图符号,表达地貌中地面线与水平面呈一定夹角的地貌区域。但是斜坡符号相对于地形图的其它符号,属于一种复杂度比较高的符号,具体表现为几何特征不唯一、结构复杂两方面[1],从而难以制作此符号。
目前学者研究制作斜坡符号的方法,主要分为两种:一是基于软件平台的符号编辑功能实现斜坡符号的绘制;二是基于编程实现斜坡符号的绘制。基于软件平台的符号编辑功能绘制斜坡符号的研究中,以AutoCAD为代表制作地形图图式符号的方法[2-4],通过定义线型文件、命令交互、人工协同可绘制出斜坡,但其过程复杂、耗时长、制图效率较低;以ArcGIS制作符号的方法中,文献[5]利用图层叠加的方法,在不同的图层上添加相应的符号效果来绘制斜坡,但是操作量大,不仅要考虑层级关系还需要考虑效果属性是否能达到不同斜坡的制图表达效果,制图效率低;文献[6]利用图形拆分的形式,分别制作斜坡的多个部件并导入符号库,通过编码调用符号部件绘制斜坡,但是制作效果与国家基本比例尺图式标准[7]有偏差;以清华山维绘制斜坡时[8],其方向线绘制有需要人工逐个指定斜坡面的转点的缺陷。为了能提高斜坡等符号绘制效率,后有了基于软件接口,进行二次开发,扩展符号化功能的研究。文献[9]基于CAD接口,解决了清华山维绘制斜坡时人工指定斜坡面转点的问题,但是依旧需要人工进行符号编辑;文献[10]基于Microstation,利用角平分线算法绘制了斜坡,但只能绘制规则的斜坡,不适用于任意形状的斜坡;还有其它类似的程序化符号绘制的研究[11-12]。二次开发软件平台的绘制功能,虽然自动化程度有一定提升,绘制斜坡等符号的效率能提高,但是受限于平台提供的接口,可扩展的符号功能有限,可以使用此方法绘制的斜坡类型也受限制。
综合来看,以上两种方法在斜坡复杂符号的制作上,受平台符号编辑以及接口限制,绘制总体效率低。因此,文中提出一种基于地理实体数据的斜坡符号自动派生方法,从全局角度得到斜坡的坡脚坡顶线和长短齿线,从局部角度优化全局的符号绘制结果,全自动派生斜坡符号。最后,经实际数据测试,验证方法有效性。
1 斜坡符号派生场景
现实世界中的斜坡有自然斜坡和人造斜坡,形状多样化,因此产生了不同的斜坡类型。由面状地理实体数据派生而来的斜坡符号,也因此有不同的斜坡符号派生处理类型,如图1所示。

图1 斜坡类型
2 斜坡符号自动派生方法
2.1 技术路线
先从全局角度出发,基于斜坡实体面数据提取主骨架线,构建主骨架线与实体面数据的点线拓扑关系,按拓扑关系提取出坡脚坡顶线,根据国标派生出长短齿线;最后,从局部角度,分析长齿线之间的相交问题和主骨架线位置问题(包括悬挂与部分不居中两种场景),优化全局式的斜坡符号派生结果,技术路线如图2所示。

图2 技术路线
2.2 全局式派生斜坡符号
全局式的斜坡符号派生内容包括两个部分:坡脚坡顶线派生与长短齿线派生。根据这两个部分,进行全局式派生斜坡符号的步骤:
1)坡脚坡顶线派生。 坡脚坡顶线来自于斜坡实体面数据的上下边缘线,因此如何提取出上下边缘线是坡脚坡顶线派生的关键。
目前有很多分析面状数据形状特征的工具,例如构建多边形Delaunay三角网[13],能够获取面状数据的边界[14],基本原理是:三角形边的左右方向如果没有邻接除本身以外的三角形,则该边为多边形的边界。但是这种方法提取得到的边界结果不是上下边缘线,需要进一步处理。
本文设计上下边缘线派生方法步骤如下:
步骤1:构建多边形Delaunay三角网,提取主骨架线。文献[15]提及了具体的提取方法,不再阐述;
步骤2:如图3所示中构建主骨架线与面实体的点线拓扑,利用主骨架线首端点s和尾端点e,将面实体数据的弧段总分为两个部分,定义主骨架线前进方向左侧为上边缘线,右侧为下边缘线。根据斜坡面实体边界上的高程信息,上下边缘线都可能是坡顶或者坡底线,根据实际情况选择即可;
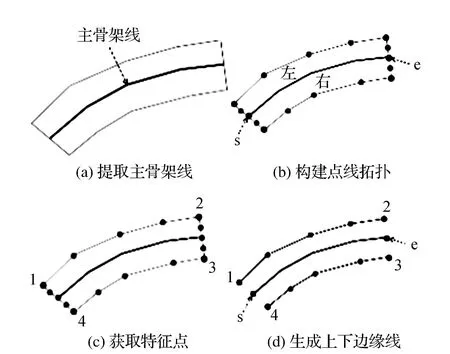
图3 派生坡脚坡顶线
步骤3:利用角度变化特征,获取斜坡实体面数据上诸如角点这样具有明显角度变化的特征点(如图3(c)的特征点“1、2、3、4”)。在文献[16]中有提及多边形的特征点提取问题与解决方法,可进行方法参考;
步骤4:删除特征点与主骨架线首尾端点间的弧段,即得到图3(d)斜坡实体面数据的上下边缘线。
2)长短齿线派生。 基于坡脚坡顶线派生结果,进一步派生长短齿线:
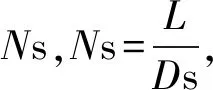
步骤2:向内延伸作各个特征点垂直于另一条边缘线的垂线,垂线距离根据上下边缘线的距离而定,即可得到多条长齿线,如图4(a)所示;
步骤3:分别在边缘线上的特征点中,两两特征点间取一个中点,向内延伸作各自中点垂直于上边缘线的垂线,垂线距离参考国标,即得到多条未加固斜坡的短齿线,完成未加固斜坡符号的派生,如图4(b)所示。
2.3 斜坡符号局部优化
全局角度的斜坡符号派生方法适用于规则型的斜坡面实体。当遇到非规则型和环型的斜坡面实体时,会出现主骨架线的位置确定和生成过程中出现长齿线形成相交问题。
2.3.1 主骨架线位置
主要在以下两种场景中出现主骨架线位置不易确定问题:
1)悬挂。 在构建面状数据的Delaunay三角网前,为了减小骨架线提取结果的扰动幅度,会对面状数据进行形状化简等制图综合处理,使用综合后的面状数据提取主骨架线,虽然扰动幅度减小了很多,但是该结果用于分析原始面状数据时,会出现悬挂,如图5所示,一是面状数据内悬挂,二是面状数据外悬挂。这种悬挂的优化方法为:内悬挂向外延伸至面状数据边界上;外悬挂向内缩至面状数据边界上。

图5 主骨架线悬挂
2)部分不居中。非规则型斜坡面实体的形状是一个不确定性问题,因此主骨架线的提取结果也存在不确定性,这种不确定性常表现在斜坡面实体的形状存在分支的时候,如图6所示,其分支所占比例即影响着主骨架线的走向。具体的处理方法为:记录方位角变化大的转点,将该转点处前后长度较短的弧段删除,再延长较长的骨架线直至面实体边界上。

图6 主骨架线走向不居中
为了斜坡符号更加均匀化,改善其因主骨架线走向,提取的坡底坡顶线不同,导致视觉效果不佳的问题。如图7所示,优化后的斜坡符号视觉效果更佳,也更加符合格式塔连续性原则。

图7 优化主骨架线走向
2.3.2 长齿线形成相交
斜坡面实体的形状不确定,因此斜坡的走向也是多样化的。当斜坡转向,且转向区域较窄时,长齿线形相交,如图8所示。

图8 长齿线相交
文献[17]通过定位交叉点,裁剪并舍弃多余的长齿线,来解决局部长齿线形成相交的问题,是一种在绘制过程中遍历长齿线来消去交叉的方法,但并不是所有斜坡情况都需要遍历,并且经裁剪后的斜坡符号视觉效果不佳;文献[18]先通过混合积确定线段相交区域,然后抽稀坡顶线上的相隔一定距离的节点作基点,再构建相交区域处的Delaunay三角网,根据三角网类型特征选取坡脚线上的节点与基点配对,解决长齿线相交问题,但是三角形类型的定义较少,坡脚线上的配对点存在其他的可能,算法存在不稳定性。
本文是基于地理实体数据绘制斜坡符号,因此解决这种问题,即可通过空间查询得到相交区域,基本原理如下:
步骤1:通过拓扑关系查询长齿线相交的区域;
步骤2:扩展相交区域至前后两条齿线;
步骤3:在扩展后的相交区域中的坡脚线上,每隔Ds距离搜索是否有一个原始节点与坡顶线上节点可配对,有则直接连接作为新长齿线;没有则在坡脚坡顶线相应进行节点加密,即等间距插入配对节点,插入节点数量为区域内的长齿线条数减去已配对的个数后得到的数量,直接对应连接坡脚坡顶线节点,如图9所示,即可解决长齿线的相交问题。

图9 消去相交
3 实 例
3.1 实验数据与环境
为验证本方法的有效性,依托中国测绘科学研究院研制的地理实体智能生产与派生平台-IGEO,嵌入一种基于地理实体数据的斜坡符号自动派生方法。方法使用的编程语言为C++,系统运行环境为MicrosoftWin7 64位操作系统,CPU为Intel Core I7-4790,单机8核8线程,主频3.6 GHz,内存8 GB,固态硬盘1 024 GB。
3.2 可视化实例
图10为本方法应用于陕西省某试验区域1∶1 000基本比例尺地形图生产中的加固斜坡符号自动派生过程。可以看出,利用垂线法直接按国标生产的齿线,在转角处常出现相交问题,经方法优化后的齿线,虽然局部间距不符合国标,但是可视化效果较前者更加良好,不影响地形图读图人员判读效果。

图10 斜坡符号派生实例
图11为试验区域的地形图局部带有其它符号的斜坡符号派生结果。结果显示,此方法派生的斜坡涵盖规则型斜坡、非规则型斜坡和环型斜坡三种,符号可视化效果好,全自动化进行,不需要再进行其它的制图编辑。

图11 试验区斜坡符号派生结果
表1为3种不同斜坡符号绘制的方法之间优缺点的定性描述与对比。基于软件符号编辑功能来绘制斜坡,相对于其它两种方法,灵活性更高,但人工计算量大;利用软件接口进行二次开发绘制斜坡,自动化程度相比前者虽有一定提升,但是依旧在绘制过程中需要人工参与;通过编程实现全自动斜坡符号派生,减少人工计算量,提高绘制效率。

表1 法定性对比
4 结束语
本文通过分析斜坡实体的形状特征,总结了3种不同的斜坡符号派生场景,包括规则型、非规则型和环型斜坡,先从全局角度派生出斜坡符号;接着再从局部角度,解决主骨架线的位置和长齿线形成相交的问题,并通过试验数据验证,该方法能适应不同的斜坡符号的派生场景,容易理解且易编程实现。
前面已提到,类似使用ArcGIS符号库加载或组合的方式,对于这种复杂的斜坡符号,绘制困难,但是实际上可以达到类似的符号效果。本方法相较于这些方式,有两点改进:①不需要借助软件接口,直接使用地理实体数据派生出斜坡符号;②当借助接口二次开发时,该方法同样适用于齿线相交问题,是一键式符号派生方法。其中除了长齿线相交处因点采样,齿线距离不符合国标以外,其余皆在国标下完成斜坡符号的派生,是新型基础测绘成果向传统成果的一次正向派生和新型应用。

