LF精炼炉双孔差流量底吹模式优化物理模拟
和炳昶,信自成,张江山,吴 军,李立民,刘 青
(1.北京科技大学钢铁冶金新技术国家重点实验室,北京 100083; 2.宝钢集团新疆八一钢铁有限公司,新疆 乌鲁木齐 830022)
生产高品质钢是当代钢铁工业的重要任务之一,炉外精炼技术在提高钢质量和扩大钢材品种方面起着关键的作用,是生产高品质钢必不可少的重要工序[1]。钢包炉底吹氩作为一种在炉外精炼中搅拌钢液的重要方法,具有促进夹杂物上浮、加快渣钢反应、加速合金料熔化的作用,以此达到提升钢水的洁净度与温度和成分的均匀度的目的[2]。针对该过程中的几个重要指标包括:混匀时间、渣眼大小、包壁冲刷等,由于钢包炉精炼过程涉及高温状态下的多相流、传质传热和化学反应,难以直接开展研究。因而根据几何相似、动力学相似等原理构建相应的物理模型是一种兼顾成本与效果,久经验证而广泛使用的研究方法。如E.K.Ramasetti等[3]通过建立了150 t底吹氩钢包的1∶5水模型,使用三种油模拟了不同性质的渣层,分别探究了单孔底吹和双孔底吹下不同渣层厚度和密度对渣眼形成的影响;董鹏莉[4]采用冷态水模拟的方法,研究了底吹孔位置对混匀时间和包壁冲刷的影响。
当前国内外实际生产中主要采用双底吹孔(透气砖)钢包炉进行精炼,但相关研究[5]发现在双孔等流量底吹模式下双流股会产生互相碰撞和干扰,一方面导致了能量耗散和搅拌效率的降低,另一方面也会导致钢液表面渣层更易卷入钢液,不利于提高钢水的洁净度。因而针对以上弊端,提出了一种双孔差流量底吹模式[6-7],该吹气模式在双底吹孔中分别以不同流量吹入氩气,使熔池内两条流股动能一大一小,形成沿某一方向的大环流,强吹流股搅拌钢液,弱吹流股则起到携带夹杂物上浮去除的作用。并通过工业试验验证了双孔差流量底吹模式相较于双孔等流量底吹模式在加快化渣、减少炉渣结壳和降低钢水全氧方面的优势。
目前,关于双孔差流量底吹模式的研究主要集中在其与双孔等流量底吹模式的对比探究,但针对差流量底吹模式相较于等流量底吹模式如何减少钢包混匀时间,以及差流量底吹模式下各因素与混匀时间之间的关系,仅存在定性描述,而缺少定量的数学模型以对差流量底吹模式进行深入研究。本文以国内某钢厂150 t钢包炉为原型制作了水模型,首先,对双孔差流量底吹模式和双孔等流量底吹模式在不同底吹孔布置方案下的混匀时间进行了比较研究;其次,运用Box Behnken Design (BBD)方法设计了关于强底吹流量、弱底吹流量、液面高度的三因素三水平实验,并利用响应面法构建了双孔差流量底吹模式混匀时间预测模型;然后,通过方差分析和响应面分析探究了各因素与混匀时间之间的关系;最后,采用所建模型优化并验证了不同钢水液面高度下的最佳强底吹流量和弱底吹流量,为LF精炼底吹氩优化提供了参考和指导。
1 实验原理
本研究以国内某钢厂150 t钢包炉为原型,基于相似性原理,制作了比例系数为1∶4的等比有机玻璃水模型,水模型底部采用弥散型透气元件,相关尺寸参数如表1所示。

表1 钢包原型和模型尺寸参数 mm
实验中使用水模拟钢液,压缩空气模拟底吹氩气,相关物性参数如表2所示。
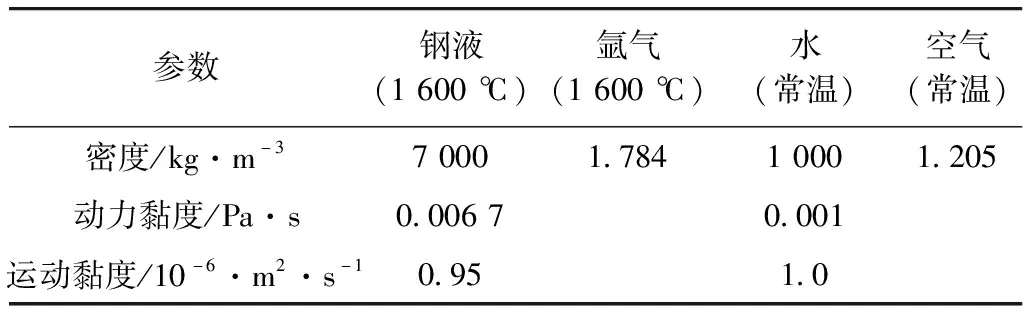
表2 介质的物性参数
为了保持原型与实验模型的动力学相似,两者的修正弗劳德准数应当保持一致,本研究的气液两相系统中修正弗劳德准数可表示为
(1)

(2)
式中:角标m为实验模型对应参数;p为工业原型对应参数。
根据式(2),原型底吹氩气流量与实验模型底吹空气流量对照如表3所示。

表3 工业原型与实验模型流量对照表 L·min-1
2 实验装置与方案
本研究使用如图1所示的装置测量钢包模型的混匀时间,其原理为将三个电极分别放置于钢包模型内部近水面的“活跃区”,底部的“滞留区”以及一个位于两者之间的“过渡区”,待实验模型加水通气3 min,钢水流场稳定后在固定位置加入定量饱和KCl溶液,同时启动与电导率仪相连的DJ800型多功能数据采集与处理系统中的电导率监测功能,即可在与之相连的计算机上得到三个电极处的电导率变化曲线。其次,对得到的电导率变化曲线进行分析,当其变化幅度不超过最终稳定值的5%时,即认定该时间为对应电极处的混匀时间。为减小设备及操作因素导致的系统误差,每组实验重复三次,每次实验取三个电极中最长混匀时间作为本次实验的混匀时间。
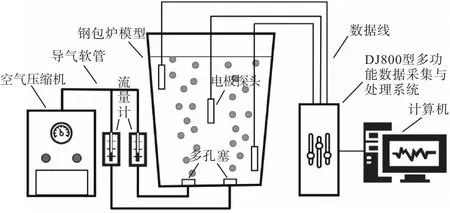
图1 装置连接图
本研究实验主要分为两部分,第一部分为对比双孔等流量底吹模式(4.3+4.3 L·min-1(标准))和双孔差流量量底吹模式(1.4+7.2 L·min-1(标准))在多种底吹双孔布置方案下(如图2所示)的混匀时间,并评估最佳底吹孔布置方案。同时,为更直观地展示并评估两种底吹模式下的流场行为,采用最佳底吹孔布置方案待流场稳定后,通过在底吹孔位置注入示踪剂,观察示踪剂在流场中的扩散行为。
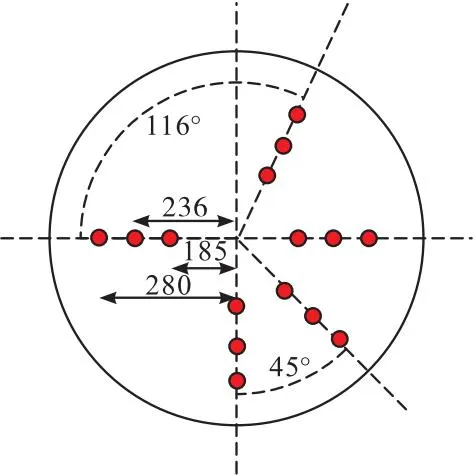
图2 底吹孔布置方案
第二部分为利用响应面法对双孔差流量底吹方案强弱流量进行分析优化。响应面法是指通过在指定设计空间内的样本点集合进行有限的试验设计,从而拟合出输出变量的全局逼近来代替真实响应面的方法,响应面法被广泛应用在各类工程优化设计中,以得到相应目标与设计变量之间的变化关系,从而得到最佳优化方案[11]。信自成等[12]通过设计冷态水模拟实验,构建了钢包炉内混匀时间和渣眼面积的响应面预测模型,得到了底吹流量、渣厚和钢水量三因素与混匀时间以及渣眼面积之间的数学关系,优化并验证了考虑混匀时间和渣眼面积的最佳底吹流量方案,证明了响应面法在定量分析钢包炉内钢液混匀时间和渣眼面积的有效性。因而本部分基于第一部分研究内容得到的最佳底吹孔布置方案,使用BBD方法设计了弱底吹流量、强底吹流量、液面高度的三因素三水平实验,并进行响应面分析,以得到各因素与混匀时间的定量数学关系,实验各因素水平和方案设计分别见表4和表5。
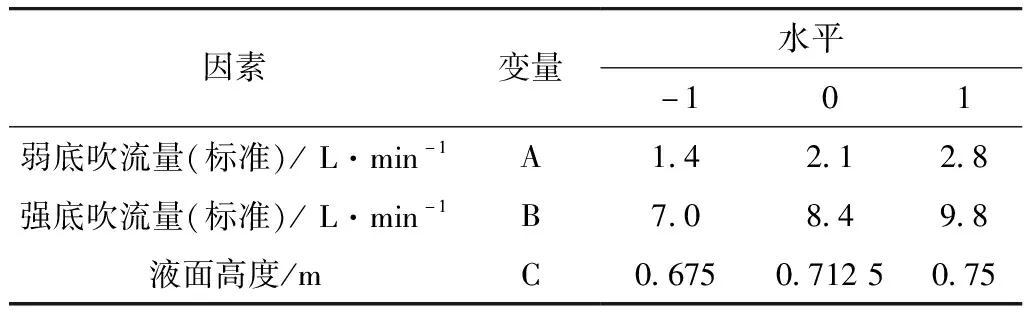
表4 实验因素编码及其水平

表5 实验设计与结果
3 实验结果分析
3.1 双孔等流量底吹模式与双孔差流量底吹模式对比
为了探究双孔差流量底吹方案和双孔等流量底吹方案对钢包混匀的影响,在保持双孔总气量相同的前提下在不同底吹双孔位置进行实验并记录相应的混匀时间,实验结果如表6所示,同时为更明显直观地进行分析,将该混匀时间对比结果按照双孔径向位置分类并绘制点线图,如图3所示。图4则比较了从底吹孔位置加入一定量示踪剂后,示踪剂在两种底吹模式下的扩散过程。
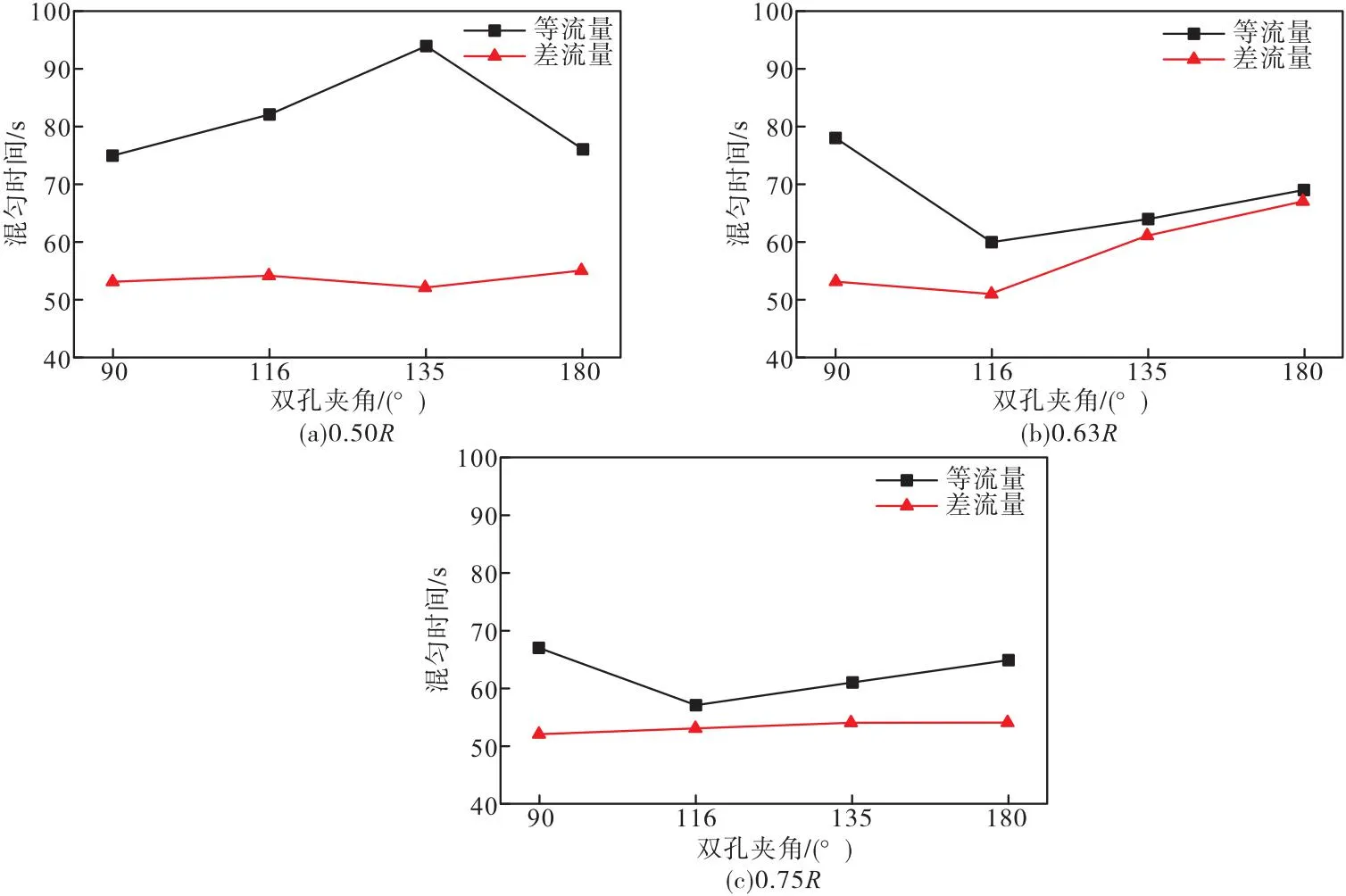
图3 混匀时间对比图

图4 双孔等流量底吹模式流场形态变化
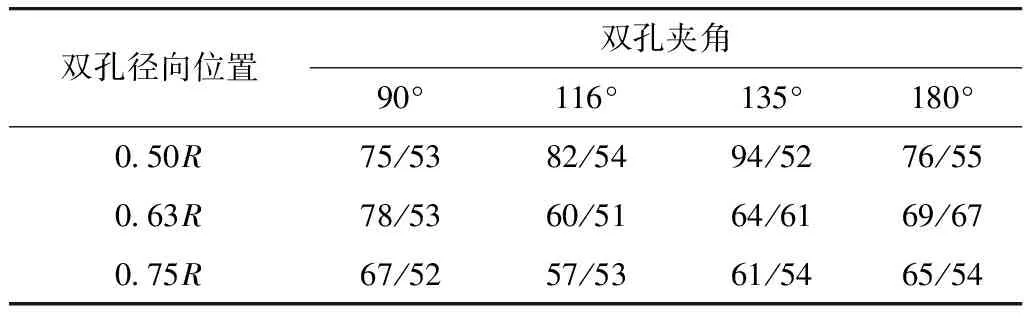
表6 双孔等流量/差流量底吹模式对应混匀时间 s
由表6可知,双孔差流量底吹模式(1.4+7.2 L·min-1(标准))在不同底吹孔布置方案下的混匀时间均低于双孔等流量底吹模式(4.3+4.3 L·min-1(标准))。其中,当双孔夹角为135°,径向位置为0.5R时,差流量模式相较于等流量模式混匀时间缩短了42 s(改善幅度约为44.68%);而在缩短幅度较小的底吹方案中,双孔夹角为180°,径向位置为0.63R时,差流量模式相较于等流量模式混匀时间缩短了2 s(改善幅度约为2.90%),该结论与唐海燕等[5-6]和胡群等[7]关于双孔差流量底吹模式的研究结果一致。同时,结合图4分析,以上现象可被解释为双孔等流量底吹模式下,双流股动能相同,虽然可以快速将底部组分携带至顶部,但形成的对称环流在钢液自由表面互相碰撞抵消(见图4(b)),反而抑制了后续钢液顶部组分向底部的迁移(见图4(c)),不利于钢液的整体混匀;而在双孔差流量底吹模式下,强吹流股形成了自强底吹孔处至弱底吹孔处的大环流(见图5(b)和图5(c)),有利于钢液整体的混匀;另一方面,通过比较图4(c)和图5(c)发现,差流量底吹模式相较于等流量底吹模式在钢包底部有更好的混匀效果,这可能是因为弱底吹流量形成的小流股由于不与强底吹流量形成的大环流发生明显碰撞抵消,主要聚集在钢包底部,促进了钢包底部钢水的混匀。

图5 双孔差流量底吹模式流场形态变化
此外,由图3可知,在等流量模式下,底吹孔排布方案对混匀时间有较大影响,当双孔夹角为116°,径向距离为0.75R时,混匀时间为57 s,在本研究所有排布方案中混匀时间最短,当双孔夹角为135°,径向距离为0.50R时,混匀时间为94 s,在本研究所有排布方案中混匀时间最长。而差流量模式的不同底吹孔排布方案对混匀时间影响相对较小,绝大多数排布方案混匀时间处于51~55 s。这是因为底吹双孔排布方案主要通过双流股干扰和包壁干扰两种方式对钢包混匀时间产生影响[4],当底吹双孔排布距离越近,双流股互相干扰现象加剧,发生偏移并互相靠近,甚至出现流股合并的情况,从而影响钢液混匀效果;而在双孔差流量底吹模式中,钢液混匀效果主要由强底吹流股影响,弱底吹流股即使与强底吹流股发生干扰,产生的影响也较为有限,因而相较于双孔等流量底吹,底吹孔排布方式对双孔差流量模式混匀时间影响较小。
目前,现行生产底吹孔排布方案为双孔夹角116°,径向距离0.63R,该方案对应等流量模式下混匀时间为60 s,在本研究所有排布方案中混匀时间较短;差流量模式下混匀时间为51 s,在本研究所有排布方案中混匀时间最短。
3.2 双孔差流量底吹模式混匀时间预测模型的建立
为进一步探究不同因素对双孔差流量底吹模式混匀时间的影响,基于BBD方法设计了关于弱底吹流量、强底吹流量、液面高度的三因素三水平实验,实验结果如表5所示。为更准确地反映各因素与混匀时间之间的关系,通过R2,Adjusted-R2和标准偏差对线性函数模型、双因子交互(two-factor interaction, 简称2FI)模型和二次模型进行了评估。其中,拟合优度R2越接近1,说明拟合效果越好;Adjusted-R2越接近1,说明模型越能充分说明工艺过程;标准偏差越小,说明模型精密度越高[13],评估结果如表7所示。

表7 模型评估结果
由表7可知,在本研究中,二次模型相比于线性函数模型和双因子交互模型可以更好地反映强底吹流量、弱底吹流量、液面高度三因素与钢包混匀时间之间的关系。基于二次模型,根据Weierstrass多项式最佳逼近定理,运用二次多项式拟合方法建立表达钢包混匀时间与强底吹流量、弱底吹流量、液面高度三因素之间关系的数学模型,其拟合回归方程见式(3)。
MT=47.4+1.25A-6.19B+0.812 5C+2AB-0.5AC+
1.13BC+3.74A2+4.86B2-0.137 5C2
(3)
式中:MT为钢包混匀时间,m;A为弱底吹流量,L/min;B为强底吹流量,L/min;C为液面高度,m。
为了进一步评估模型的可靠性,对该二次模型进行方差分析,结果如表8所示。
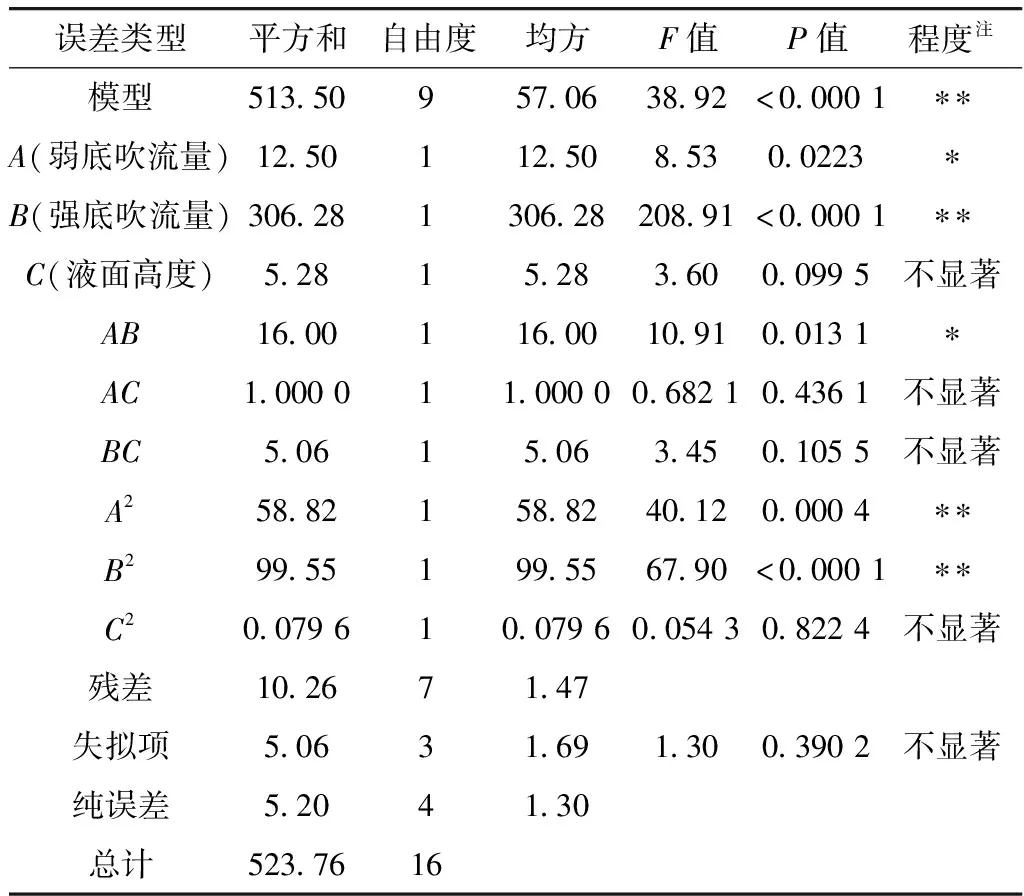
表8 ANOVA分析表
由表8方差分析结果可知,模型整体的P值小于0.01,失拟项P值大于0.05,表明该模型整体是显著的,且拟合精度较好,可以利用该模型对双孔差流量底吹模式进行分析优化。此外,由方差分析结果可知,各因素对混匀时间的影响由强到弱分别为:强底吹流量、弱底吹流量、液面高度。图6为混匀时间残差的正态概率分布图,反映了残差的实际累积概率与理论累积概率的符合程度,如果图6中各点为直线或接近直线,则样本正态分布假设可以接受,图6中混匀时间残差的实际累积概率大致分布在一条直线上,说明误差符合正态分布,模型适应性良好,图7为实际测得混匀时间和模型预测混匀时间,两者基本处于一条直线上,Adjusted-R2为0.955 2,Predicted-R2为0.829 8,两者差值小于0.2,表明实验数值与预测数值较为吻合,说明基于响应面法的混匀时间预测模型是可靠的[15]。
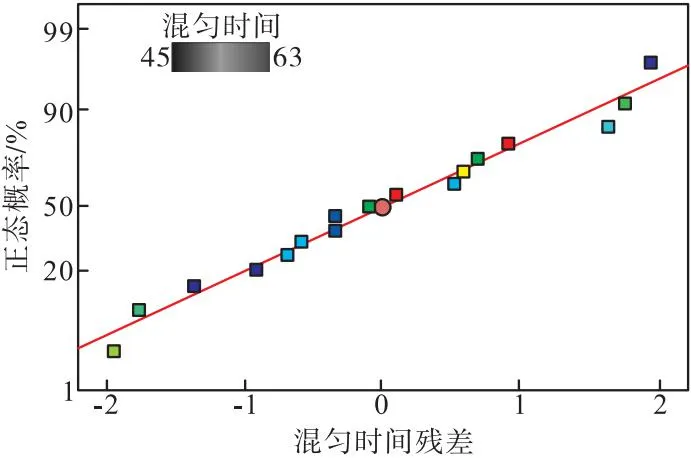
图6 混匀时间残差正态概率分布图

图7 混匀时间实际值与预测值对比图
3.3 双孔差流量底吹模式响应面分析
响应面法的一个优点是可以通过将单个因素固定在中心值,得出其他两个因素的三维响应面和等高线图,进而分析两因素之间的交互作用及其对混匀时间的影响[14],图8所示为当液面高度为0.712 5 m(对应实际生产钢水量为150 t)时,强底吹流量和弱底吹流量的交互作用响应面。图8(a)为混匀时间三维响应面图,三维响应面在某个方向上越陡峭,则表明该方向的因素对混匀时间的影响越显著;图8(b)为混匀时间等高线图,等高线越接近椭圆,则两个因素之间的交互作用越强[15]。
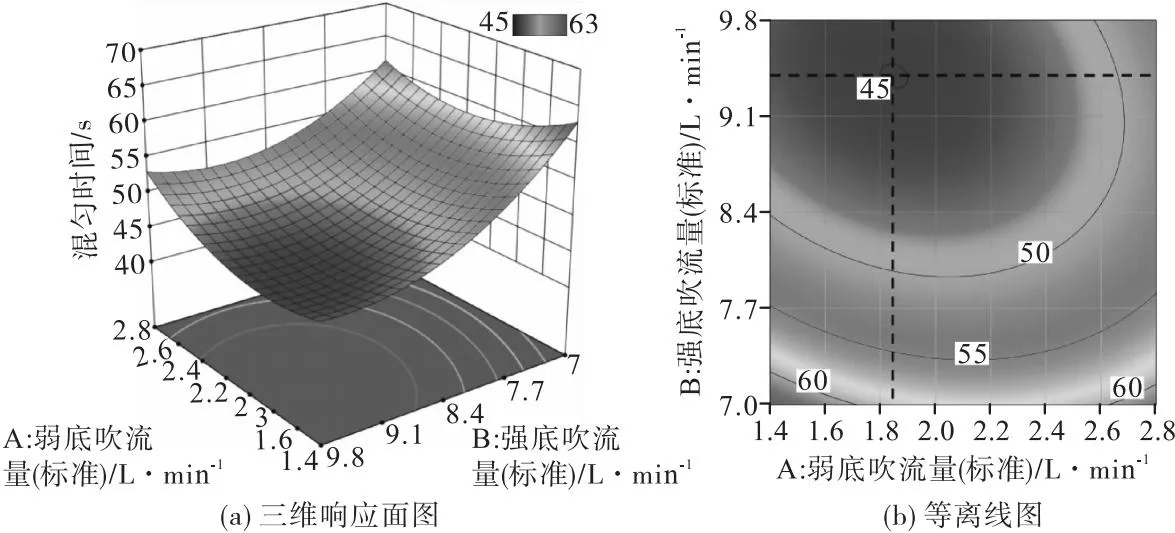
图8 弱底吹流量和强底吹流量对混匀时间的交互影响
分析图8可知,相比于弱底吹流量,强底吹流量对混匀时间影响更为显著;弱底吹流量与强底吹流量之间存在较为显著的交互作用,同时,该结果与方差分析结果一致。由图8(a)可知,强底吹流量方向上的响应面斜率更高,即在差流量底吹模式下钢包混匀时间主要由强底吹流量决定。由图8(b)可知,随着强底吹流量从7.0 L·min-1(标准)增加到9.8 L·min-1(标准),混匀时间总体呈现出降低的趋势,这是因为在差流量底吹模式中,主要搅拌能由强底吹流股生成的大环流提供,更高的强底吹流量会带来更高的搅拌功率,从而缩短钢液混匀时间[7];但同时也应注意到,在强底吹流量超过9.1 L·min-1(标准)后,钢液混匀时间降低出现减缓现象,甚至出现了升高的趋势,这是因为当强底吹流量超过一定临界值后,作用于钢包混匀的搅拌功达到上限,混匀时间不再随之降低,并且继续增加的搅拌能则作用于包壁和钢渣混匀,反而会影响钢水洁净度[16]。而对于弱底吹流量,尽管其相较于强底吹流量对混匀时间影响较小,但仍呈现出了一定的规律性,当其流量低于1.83 L·min-1(标准)时,随着弱底吹流量的增加,相应混匀时间也随之降低,这可能是因为当弱底吹流量较小时,弱底吹流股被强底吹流股形成的环流压制,主要集中在钢包炉底部,反而促进了钢包炉底部死区钢水的混匀;而当弱底吹流量超过1.83 L·min-1(标准)时,随着弱底吹流量的增加,相应混匀时间反而增高,这可能是因为弱底吹流股形成的环流逐渐增大并与强底吹流股形成的环流发生互相干扰耗散,整体流场行为向双孔等流量底吹模式靠拢,从而降低了作用于钢液混匀的搅拌功比率。
3.4 差流量底吹方案优化与实验验证
钢水混匀时间越短越有利于快速均匀钢水温度和成分,从而提高精炼效率,降低生产成本。从3.3节分析可知,双孔差流量底吹模式下的混匀时间受到强底吹流量和弱底吹流量的交互作用影响,针对其开展优化需要根据上文构建的数学关系进行具体分析,本节基于构建的混匀时间预测响应面模型,如式(3)所示,利用Design Expert软件中的Optimization功能,以最短混匀时间为目标,在不同的液面高度(钢水量下)得出对应的强底吹流量和弱底吹流量:①当液面高度为0.675 m(对应工业原型钢水量为140 t)时,对应的强底吹流量为9.50 L·min-1(标准),弱底吹流量为2.19 L·min-1(标准),混匀时间为44 s;②当液面高度为0.712 5 m(对应工业原型钢水量为150 t)时,对应的强底吹流量为9.48 L·min-1(标准),弱底吹流量为1.83 L·min-1(标准),混匀时间为45 s;③当液面高度为0.75 m(对应工业原型钢水量为160 t),对应的强底吹流量为9.20 L·min-1(标准),弱底吹流量为1.92 L·min-1(标准),混匀时间为46.5 s。为进一步验证钢水混匀时间预测响应面模型的可靠性,在上述钢包底吹氩最佳优化方案的基础上,开展了水模拟实验,并将实测值与预测值进行比较,结果如表9所示。

表9 最佳优化方案的预测值与实测值
由表9可知,预测值和平均实测值的误差均在4%以内,说明该响应面模型是可靠的,也证明了应用该模型对差流量底吹模式流量进行优化是可行的。
4 结 论
(1)在双孔总气量相同的情况下,相较于双孔等流量底吹模式,双孔差流量底吹模式在本研究中所有底吹孔布置方案下都会缩短钢包的混匀时间,且最高缩短幅度为44.68%,最低缩短幅度为2.90%;相较于双孔等流量底吹,底吹孔排布方式对双孔差流量模式混匀时间影响较小。
(2)通过BBD设计了三因素三水平实验方案,基于响应面法构建了弱底吹流量、强底吹流量、液面高度三因素的钢包混匀时间预测模型,该模型p值小于0.01,Adjusted-R2为0.955 2,Predicted-R2为0.829 8,模型拟合效果较好。由方差分析及响应面分析结果可知,各因素对钢包混匀时间影响由强到弱依次为:强底吹流量、弱底吹流量、液面高度,且双孔差流量底吹模式下的混匀时间受到强底吹流量和弱底吹流量的交互作用影响。
(3)应用构建的混匀时间预测响应面模型,以最短钢包混匀时间为目标,得到了三个液面高度下相应的最优弱底吹流量和强底吹流量方案以及相应的混匀时间,并基于该优化方案进行了水模实验,结果表明,实测值与模型预测值较为吻合,误差均在4%以内,进一步证明了响应面模型的可靠性,也表明运用响应面法对双孔差流量底吹流量进行优化是可行的。

