脉内步进频信号非均匀间歇转发干扰特性研究

冯佳美 徐飞

DOI：10.19850/j.cnki.2096-4706.2024.02.013

收稿日期：2023-10-29

摘  要：随着数字射频存储技术的快速发展，间歇采样转发干扰凭借其突出的欺骗和压制效果，在实际的干扰场景中有广泛的运用，对雷达的识别和探测造成了严重的威胁。区别于常规的均匀间歇干扰，采样信号非均匀的样式进一步拓展了干扰的灵活性和欺骗性，对雷达有更明显的干扰压制效果。通过研究雷达发射脉内步进频信号和非均匀间歇采样转发干扰类型的产生机理，对其脉压后的时频特性进行分析，最后通过仿真实验对脉内捷变步进频受到非均匀间歇采样干扰的效果进行验证。

关键词：线性步进频；非均匀间歇采样转发干扰；时频域分析；匹配滤波

中图分类号：TN974  文献标识码：A  文章编号：2096-4706（2024）02-0054-06

Research on Non-uniform Intermittent Forwarding Interference Characteristics of Intra-pulse Step Frequency Signal

FENG Jiamei， XU Fei

（Xi'an Electronic Engineering Research Institute， Xi'an  710100， China）

Abstract： With the rapid development of DRFM technology， and its outstanding deception and suppression effect， intermittent sampling and forwarding interference has been widely used in actual interference scenarios， which poses a serious threat to radar identification and detection. The non-uniform pattern of the sampling signal further expands the flexibility and deception of interference， and has a more obvious interference suppression effect on radar which is different from the conventional uniform intermittent interference. Through studying the generation mechanism of the in-pulse step frequency signal and non-uniform intermittent sampling and forwarding interference types in the radar transmission， this paper analyzes the time-frequency characteristics after pulse pressure. Finally， the degree of in-pulse agile step frequency interfered by non-uniform intermittent sampling is verified by simulation experiments.

Keywords： linear step frequency; non-uniform intermittent sampling and forwarding interference; time-frequency domain analysis; matching filtering

0  引  言

当前电磁环境复杂多变，干扰和抗干扰技术一直在交替改进，关于二者的相关研究也不断深入，为了尽可能降低干扰带来的影响，更好地实现雷达的识别和探测功能，需要在波形设计和信号处理两方面进行抗干扰的处理，前者的改进思想主要是降低目标回波和干扰回波的相关性，手段包括发射脉间捷变、脉内捷变、脉间脉内捷变，步进频、锯齿波等复杂信号来增强自身的复杂性、灵活性，脉内捷变将雷达信号单个脉冲划分为多个子脉冲，子脉冲载频随机变化，不再是固定的线性频率，而脉间捷变是通过发射正交信号，各个子载波之间进行掩护，进而降低干扰对雷达探测和识别的影响；后者的核心就是通过利用目标回波和干扰的能量方面的区分度进行重构和抑制，一方面是估计干扰的参数重构干扰信号，接收到的回波减去干扰来实现抑制，需要估计的参数包括采样周期、采样占空比、带宽、脉冲宽度等参数，另一方面是先减去干扰和被干扰影响的目标部分，再重构目标信号，剔除被干扰的目标信号会造成较大的脉压损失增益，利用重构来弥补这部分损失，进而实现对干扰的抑制。

波形和信号处理方面的抗干扰工作逐步深入，同時也推动了干扰工作的复杂化，干扰采样方式分为全脉冲间歇采样和间歇采样，全脉冲采样（FSRJ）将截获到的整个脉冲信号进行存储、调制和转发，因此脉内捷变频信号对其无效，但脉间捷变对目前使用较为广泛的采样、转发时间间隔更短的间歇采样干扰没有很理想的效果，需要利用脉内捷变频信号来对干扰进行更为有效的干扰对抗，脉内捷变频将线性调频信号切割后的子脉冲随机排列，信号排列样式由编码信号确定，既保有线性调频信号在探测距离和分辨率上的优点，又能增加发射波形的灵活性，具有较强的抗干扰能力，极大地增加了雷达发射信号的随机性。非均匀间歇采样转发干扰技术也是基于欠采样原理的相干干扰技术，区别于均匀采样的间歇采样转发干扰，其采样具有伪随机性，灵活度更高，欺骗和遮蔽效果更强，因此非均匀采样的实际运用也十分广泛。在采样方式非均匀的基础上，转发干扰方式又可以分为定量和不定量转发，以此来增强干扰的效果，本文主要研究脉内捷变步进频信号受到非均匀间歇干扰后的特性。文献[1]针对线性调频信号被非均匀周期转发干扰后的特性进行分析，仿真实验表明对目标回波造成了强有效的干扰，文献[2]利用子脉冲进行脉压，通过信号处理端的加权处理进行干扰抑制，文献[3]是针对LFM信号的非均匀非周期的干扰形式，脉压仿真结果表现了较强的欺骗和压制干扰效果，文献[4]发射信号为脉内线性调频信号分为多个子脉冲信号，进行随机重排之后的脉内频率捷变信号被均匀间歇采样转发干扰后的时频图进行分析，利用能量阈值分割的方法对干扰进行抑制，文献[5]和文献[6]对脉内步进频经过脉冲压缩和相参积累后的特性进行分析，提高了识别和追踪的能力，文献[7]针对多种复杂波形和复杂干扰样式进行仿真优化设计，利用遗传模拟退火算法实现了一定的抗干扰效果，文献[8]到文献[11]从信号处理时频域的角度对干扰进行了抑制分析，文献[12]利用最大类间方差法对脉内捷变频信号干扰进行抑制。目前已经有较多的关于线性调频信号在受到均匀以及非均匀间歇转发干扰之后的仿真研究，本文主要对脉内步进频信号被非均匀间歇干扰类型信号干扰后的特性进行分析。

1  脉内步进频

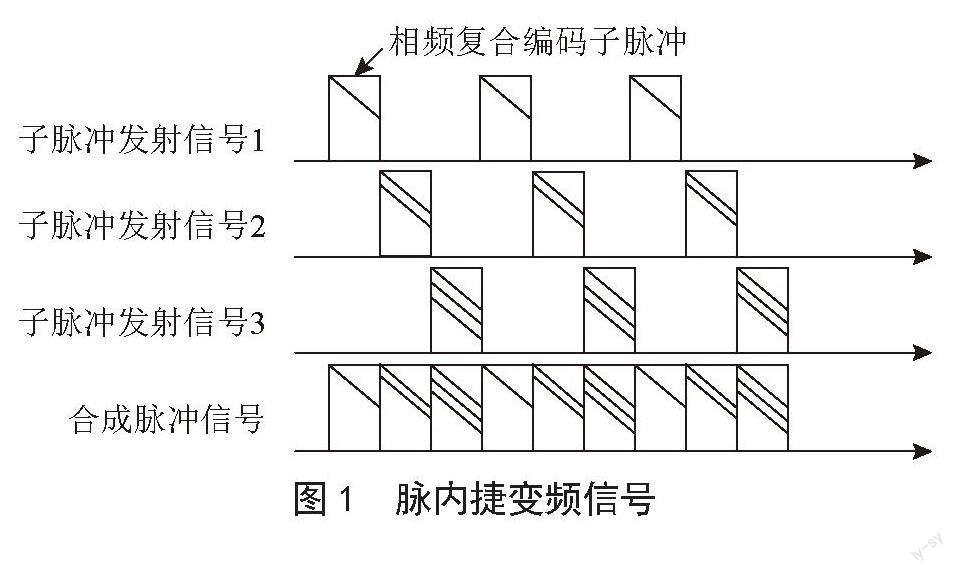
LFM信号具有大时宽带宽积的特点，可以解决雷达作用距离和距离分辨率之间的矛盾，线性调频步进频雷达发射载频线性跳变的脉冲串，脉内的常载频子脉冲换成了线性调频子脉冲，每个子脉冲都是线性调频，子脉冲的中心频率均匀步进，如图1所示，脉内捷变频信号脉冲信号分为多个子脉冲。

线性调频步进频回波信号：

（1）

其中Tr為脉冲重复周期，Δf为频率步进大小，k = B / T为子脉冲调制频率，N为调频子脉冲个数，将第n个脉冲沿时域截取为M段，每个子脉冲脉宽为：Tsub = Tp / M，带宽为：Bsub = B / M，这里的子脉冲选用的是线性步进频，则第m段子脉冲的时域表达式为：

（2）

如图2所示，线性调频步进频有线性调频的高距离分辨率等优点，兼具线性调频和步进频率信号的优点，在不增加带宽的情况下既保证了足够大的作用距离，又能够形成高分辨率的距离像，具有较强的抗干扰能力。

2  间歇采样转发干扰类型

2.1  非均匀采样定量转发干扰

间歇采样干扰可以在目标左右两边出现，既有超前的又有滞后的干扰，目前间歇干扰的方式包括均匀采样、非均匀采样、周期交替采样、参差周期间歇采样干扰、间歇采样逐次循环转发干扰、间歇采样非均匀重复转发干扰等干扰样式，如图3所示，非均匀的采样脉冲由m序列产生，相连的1作为采样脉冲的宽度，最终得到非均匀的采样脉冲串。

非均匀间歇采样脉冲串为：

（3）

式中τ为编码码元宽度，n为码元编号，?为卷积运算，an为随机的{0，1}编码序列。一个脉宽内总编码数量为N = T / τ，频谱为：

（4）

图4为定量转发的非均匀采样转发干扰信号，干扰机在每个脉冲重复间隔（PRT）内共产生K个采样脉冲，对第k个采样脉冲，采样脉宽为τk，进行M次转发，则采样周期为：Tsk = （M + 1） τk。

非均匀采样定量转发干扰信号：

（5）

如图5所示，均匀采样信号和非均匀采样信号在时域上的分布差异，图6（a）是非均匀采样干扰信号在时域上的不均匀随机信号，图6（b）表明非均匀信号在频域上的连续性。

1）当f = 0，非均匀间歇采样脉冲的频谱峰值为：

（6）

式中N0为an中非零码元的个数，η为采样脉冲串的占空比，这意味着非均匀采样脉冲串的频谱峰值与采样脉冲占空比呈正相关。

2）不同于均匀间歇采样脉冲串频谱的离散分布，非均匀间歇采样脉冲串在频谱上具有连续性。

2.2  非均匀采样不定量转发干扰

非均匀间歇采样脉冲串由m序列产生，具体产生方法就利用序列的随机性，取相连的1作为采样脉冲的宽度，最终得到非均匀的采样脉冲串，采用的非均匀和不定量采样转发，最大程度上破坏了脉压的规律性。不定量转发的非均匀间歇采样转发干扰如图7所示。

首先对截获到的信号进行K次非均匀间歇采样，每次采样的宽度为τk，每次采样后转发的次数为mk，将发射信号按照脉冲宽度进行切片，第k次采样转发干扰的总时间为：

（7）

转发次数为K次，采样的子脉冲长度为τk，则前k-1个采样以及转发的总时间为：

（8）

此时间歇采样脉冲信号为：

（9）

区别于传统的干扰，此时采样脉冲不再是周期函数，频谱不能用傅里叶级数表示，相应的采样信号为：

（10）

第k个采样信号复制Mk次，总的干扰信号为：

（11）

an为伪随机的{0，1}二相码，n为码元的编号，N0为零码元的个数， 为占空比。非均匀采样定量转发干扰是个不一样的采样宽度进行不同次数的重复转发，非均匀重复干扰就是mk个不一样的采样宽度进行重复转发。

3  仿真实验分析

3.1  定量转发干扰脉压

线性调频步进频雷达发射载频线性跳变的脉冲串，每个子脉冲都是线性调频，脉冲压缩是回波信号与雷达发射信号的时域互相关，对回波信号首先子脉冲压缩，然后进行脉冲串间的相参合成，既保留子脉冲低采样率和窄带处理的优点，又具备线性调频信号大时宽带宽积特点。

脉冲压缩信号为ys（t） = xs（t） h（t） = x（t） pT （t） h（t），采样处理为xT （t） = pT （t） s（t），频谱为XT （ f ） = PT （ f ） ? S（ f ），考虑匹配滤波器为hT （t） = s*（-t），其频谱HT （ f ） = S*（ f ），则其匹配滤波输出为：

（12）

雷达信号的模糊函数：

（13）

匹配滤波输出后：

（14）

峰值点出现在：

（15）

相邻两阶ysn（t）峰值相距：

（16）

非均匀周期采样后第一次转发的干扰信号经过匹配滤波后的输出：

（17）

其中τ0为第一个假目标的延迟时间，T为雷达的脉冲宽度，后续转发干扰信号脉压的输出结果为 （t-τm），m = ±1， …， ± n，则定量转发后的干扰信号脉压结果为 ，从式子可以看出在雷达接收机这里产生了2n个幅度不等的主假目标，每个假目标的幅度都和其转发脉冲的宽度成正比，假目标之间的间隔为τ，为了使各主假目标互相压制，可以通过调整采样脉冲宽度τ和转发延迟时间τd参数来达到该目的。第一次转发脉冲延迟的时间与干扰机和目标的距离Rjt有关，最左侧主假目标与真目标距离为 ，所以各个主假目标的延迟时间为 ，z = 1， …， 2n，因此干扰机和目标的间距不小于 ，即 ，可知：

1）YT（ f ）的峰值与LFM步进信号匹配滤波的峰值关于采样脉冲占空比呈正相关。

2）非均匀采样脉冲串频谱的连续性对线性步进频信号施加了连续的多普勒平移，因此其匹配滤波输出在一定范围会形成高水平的旁瓣，由采样脉冲串频谱主瓣宽Bmain = 2 / τ，干扰信号的匹配滤波输出旁瓣覆盖范围为Δt = 4 / kτ，形成了更加大范围的干扰效果。

3.2  不定量转发干扰脉压

非均勻间歇信号的频谱输出与采样信号占空比呈正相关，占空比越高，峰值输出越高。

干扰信号为：

（18）

采样转发信号为：

（19）

由两部分组成，第一项与雷达发射信号频谱幅度呈正比，第二项是对发射信号进行连续搬移，相对于均匀采样转发的匹配滤波，直接利用发射信号作为滤波器进行相参积累，非均匀匹配滤波是通过对每一段采样信号转发后的结果进行匹配滤波：

（20）

第k个采样信号第m次转发之后的脉压结果的主瓣中心为 ，第k次干扰信号脉压结果为：

（21）

总的非均匀不定量各个子脉冲干扰信号脉压叠加的结果为：

（22）

由公式推导可知，非均匀不定量脉压的效果更具压制和欺骗效果。

为了验证非均匀采样转发干扰的效果，主要仿真参数设置如表1所示。

均匀采样直接转发干扰脉压结果和均匀采样重复转发干扰脉压结果如图8和图9所示，非均匀采样定量转发和不定量转发的脉压结果如图10和图11所示。

由图8和图9可以得出，第k个采样信号第m次转发之后脉压的中心位于 ，幅度为τk / 2，主瓣宽度为2 / μτk，旁瓣中心幅度为 ，对于均匀采样转发，每一次的时宽τk都相同，具有相同转发次数的采样信号脉压后的位置是相同的，因此干扰的效果会在相同的位置不断得加，形成较高的峰值，反倒易于被识别出来，而非均匀不定量转发，采样时间不同，转发次数不同，脉压之后的旁瓣、主瓣位置都不相同，有效压制范围远大于均匀采样干扰，由图10和图11可知，干扰具有很强的压制和欺骗效果。

4  结  论

本文非均匀间歇转发干扰的实现基于m序列编码信号，编码序列的灵活性和转发次数的随机性极大增强了干扰的欺骗和压制效果，最后的仿真实验结果也表明了非均匀干扰较均匀干扰对步进线性频信号的显著干扰性能。

当前随着抗干扰技术的蓬勃进展，雷达发射信号的波形样式多样，具有不同的特性，即使采用相同参数的非均匀间歇采样转发干扰，不同波形被干扰的效果也不一样。本文仅对步进线性频信号受到干扰后的特性进行了仿真分析，下一步可以对更加复杂的脉内编码跳频信号受到干扰后的特性进行分析，同时通过改变干扰的参数，定量分析参数变化对不同波形干扰效果的影响。

参考文献：

[1] 张养瑞，李云杰，李曼玲，等.间歇采样非均匀重复转发实现多假目标压制干扰 [J].电子学报，2016，44（1）：46-53.

[2] 吴传章，陈伯孝.间歇非均匀采样转发干扰产生方法研究 [J].系统工程与电子技术，2021，43（1）：1-10.

[3] 李惠东，赵忠凯.一种针对LFM雷达的非均匀间歇采样干扰样式 [J].应用科技，2020，47（3）：37-40+45.

[4] 陈峰，张旭威.捷变频雷达抑制间歇采样转发干扰技术研究 [J].舰船电子对抗，2022，45（4）：26-31.

[5] 孙宗正，刘智星，肖国尧，等.非均匀间歇采样转发干扰对脉内捷变雷达影响分析 [J/OL].系统工程与电子技术：1-15（2023-09-07）.http：//kns.cnki.net/kcms/detail/11.2422.tn.20230906.1733.016.html.

[6] 郭慧峰，鲁永为，山世浩，等.对线性调频步进频雷达相参干扰方法研究 [J].航天电子对抗，2022，38（1）：52-54+59.

[7] 张彦，叶春茂，李璋峰，等.多种转发干扰下的脉内脉间波形综合优化设计 [J].系统工程与电子技术，2022，44（5）：1495-1501.

[8] ZHAO S S，LIU N，ZHANG L R，et al. Discrimination of Deception Targets in Multistatic Radar Based on Clustering Analysis[J].IEEE Sensors Journal，2016，16（8）：2500-2508.

[9] 张亮，王国宏，杨志国，等.利用回波时频相关差异的雷达欺骗干扰识别方法 [J].西安交通大学学报，2021，55（2）：136-142.

[10] GONG S X，WEI X Z，LI X. ECCM Scheme Against Interrupted Sampling Repeater Jammer Based on Time-frequency Analysis [J].Journal of Systems Engineering and Electronics，2014，25（6）：996-1003.

[11] LIU K Q，FU X J，GAO Z M，et al. Time-space Two-dimensional Dense False Targets Jamming and Countermeasures [C]//2018 13th IEEE Conference on Industrial Electronics and Applications （ICIEA）.Wuhan：IEEE，2018：1982-1987.

[12] 董淑仙，全英汇，沙明辉，等.捷变频雷达联合脉内频率编码抗间歇采样干扰 [J].系统工程与电子技术，2022，44（11）：3371-3379.

作者简介：冯佳美（1999.10—），女，汉族，山西吕

梁人，硕士研究生在读，研究方向：雷达抗干扰；徐飞（1983.

12—），男，汉族，安徽阜阳人，研究员，硕士研究生，研究方向：数字信号处理。