基于二阶链式子区的金属拉伸试验DIC 辅助测试方法

李得睿，周焕新，程 斌

(上海交通大学船舶海洋与建筑工程学院，上海 200240)

金属材料拉伸试验是测定金属多种材性指标的重要量化方法，是科研、工程领域最为常用的试验方法之一[1-6]。目前传统金属拉伸试验仍采用拉伸试验机与引伸仪相结合的测量方式，针对金属材料的弹性阶段材性指标进行高精度测量。传统拉伸试验需在试件表面安装位移测量传感器，其中以引伸仪应用最为广泛。引伸仪的规格与精度密切相关，实验前需要根据试件长度选择量程适宜的引伸仪。塑性能力较好的金属试件伸长量一般大于引伸仪量程，必须在试验过程中提前拆卸引伸仪。同时，对于颈缩量、极限伸长量等金属材性参数，往往需要借助人工手段进行量测。对于金属拉伸试验的塑性阶段变形量测，如真实应力-应变曲线，目前鲜见出现通用的自动化高精度测量手段。

数字图像相关(Digital Image Correlation, DIC)技术，是21 世纪以来实验力学领域内学术研究最为活跃、实际应用最为广泛的光测力学技术之一[7]。自20 世纪80 年代起，经过全世界众多学者不断地创新与实践，逐渐形成了一套具备完整理论体系的数字光测力学技术，即DIC 技术。BRUCK等[8]于1982 年提出了正向牛顿拉夫森 (Forward Additive Newton–Raphson, FA-NR)算法，自此确立了DIC 核心算法基础。PAN 等[9]于2013 年在FA-NR 的基础上提出了反向组合高斯牛顿 (Inverse Compositional Gauss–Newton, IC-GN)算法，显著降低了运算量。LEWIS 等[10]于1995 提出的快速归一化互相关 (Fast Normalized Cross Correlation, FNCC)算法，逐步成为目前主流的DIC 整像素匹配算法。此外，全局DIC[11]、立体DIC[12]与数字体积相关(Digital Volume Correlation, DVC)技术[13]相继问世，各类DIC 应变计算方法[14-15]也依据各种应用场景陆续被提出。从应用角度来看，目前应用最为广泛的DIC 技术为多点DIC[16-18]与全场DIC[7,18]。

DIC 技术本质在于追踪一块像素子区内的随机像素纹理，并基于形函数、相关度函数与最优化理论对这块像素区域的形变进行最优量化逼近。DIC 对数以万计的小像素子区进行形变测量，便可组成形变场。因此，DIC 天然适用于测试大面积的全场形变，目前全场DIC 测试技术已广泛应用于具有全场形变测量需求的力学实验场景[7]。然而，在金属拉伸试验领域，DIC 技术仍限于学术研究[19-22]，未实现工业化普及应用。本质原因有四点：1) 过度冗余计算。全场DIC 技术采用“小子区，多子区”的量测理念，导致各个子区之间存在高度重合区域，而金属拉伸试验无需观察全场形变结果，因此，将全场DIC 用于金属拉伸试验，存在过度冗余计算问题； 2) 缺乏针对性算法。将DIC 的形变测量结果转化为金属材性结果，需要针对性地提出相应计算理论与方法，进而测得弹性模量、颈缩量、伸长量、真实应力-应变曲线等金属材性指标，目前相关研究鲜有报道；3) 缺乏专用测量系统。金属拉伸试验场景往往需要测试多根金属试件并实时得到试验结果，这就要求试验场景配备专用软件及设备，满足高效、轻量、便捷、自动的测量需求，目前各类通用全场DIC 测试系统[18,23]显然无法满足相关需求；4) 不具备良好测量条件。全场DIC 测试技术依靠数以万计的小像素子区密集排列进行全场形变量测，因此图像内试件成像区域宜具备可观的宽度和高度，显然长条形金属试件难以满足此条件。综上，现阶段实验力学领域主流的全场DIC 测试技术并不适用于传统金属拉伸试验。因此，将DIC 技术引入金属拉伸试验，提出相应计算理论，实现基于DIC 的自动化金属材性辅助测试技术，具有实际意义。

本文基于“大子区，少子区”的量测理念，提出基于二阶链式子区的DIC 金属拉伸辅助测试理论与技术，凭借理论清晰、无冗余计算等特点，将DIC 合理地深度应用于金属拉伸试验中，以替代传统试验中的引伸仪，实现弹模、颈缩量、伸长量、真实应力-应变曲线等金属材性指标的自动化测量。

1 理论方法

金属拉伸试验的数据组成可分为力与形变两部分。规范《金属材料拉伸试验第1 部分：室温试验方法》[24](GB 228.1-2010)(以下简称《规范》)内所规定的各类测量指标(如屈服强度、伸长率、屈服点延伸率等)，均为力、形变或二者结合的测量结果。真实试验场景下，试件受力大小可通过拉伸试验机实现自动化测量，而试件形变则需借助引伸仪及人为手段进行辅助测量，这对拉伸试验的试验效率及测量精度造成了较大影响。

为了将DIC 引入金属拉伸试验，本文针对性地提出一种形变测量理论，该理论适用于金属试件受拉力作用下的形变测量，测量内容涵盖《规范》规定的伸长率、截面收缩率等多个金属拉伸基本形变指标。该理论可基于DIC 技术进行实现，从而实现自动化形变测量。

1.1 链式形变测量理论

假想存在一种完全柔性且具有黏性的链条，将这种柔性链条粘贴于物体表面后，此柔性链条可忠实地跟随物体表面的形状变化而发生形变。

现将柔性链条粘贴于金属试件的竖向平行段，共计粘贴两条，其初始长度均为原始标距L0，粘贴方向平行于试件竖向平行段，两链条的初始宽度为D0，如图1(a)所示。在试件表面建立直角坐标系xoy，坐标系x轴平行于试件竖向平行段，原点o位置任意，如图1 所示。初始时刻两柔性链条在坐标系xoy内的曲线方程为fL,0(x)与fR,0(x)，如图1(a)所示。

图1 柔性链条示意图Fig.1 Sketch map of flexible chain

当试件在轴向拉力作用下发生形变后，如图1(b)所示，在t时刻，原始标距长度变为Lt。伸长率Ep可表示为：

在t时刻名义线应变 ε¯nom,t为：

式中：SL,0为初始曲线长度；SL,t为t时刻曲线长度；下标L、R 表示左链或右链；x0,t为t时刻曲线积分下界； ε¯nom,t为t时刻试件名义线应变。

对于t时刻柔性链条，存在颈缩处极值点。设fL,t(x)与fR,t(x)的极值点坐标分别为(xL,max,yL,max)与(xR,max,yR,max)，此时有：

式中，Dt为两柔性链条沿y轴方向的最短间距。

设沿着fL,t(x)与fR,t(x)的各处应变为 εL,t(x)与εR,t(x) ，此时可得颈缩处应变 εneck,t为：

式中： εneck,t为t时刻颈缩处应变；xL,max与xR,max为fL,t(x)与fR,t(x)的极值点横坐标。同时，本式采用均值化处理，可同时适用于双链的理论对称情形及实际近似对称情形。

设轴拉试件沿坐标系xoy法向(厚度方向)的t时刻颈缩处收缩率与y轴方向的t时刻收缩率之比为µt，即：

式中：B0为试件初始等效厚度；Bt为t时刻试件颈缩处等效厚度，则无论何种截面形状的试件，其在t时刻的颈缩处截面最大收缩率为：

设t时刻拉伸试验机测得力为Ft，则t时刻金属试件最大轴向拉应力，也即颈缩处应力σneck,t为：

式中：S0为试件初始横截面积； σneck,t为均匀分布情形下的颈缩处应力。

绘制 σneck,t-ε¯nom,t及 σneck,t-εneck,t曲线，即可得相应的应力-应变曲线。

需要说明的是，《规范》中对伸长率的定义为原始标距的伸长量与原始标距之比的百分率，这一概念可认为是试件在弹性阶段的应变以及在其余阶段的名义应变。然而，试件在塑性阶段的各处轴向应变均不同，且存在颈缩段，所以本文所提理论在式(2)中采用曲线积分长度与原始曲线长度之比，作为试件塑性阶段的名义线应变，是对《规范》中伸长率概念的合理延申。另一方面，WANG 等[20]运用数值计算方法模拟了标准金属拉伸试件轴拉过程，结果显示试件颈部最小截面的von-Mises 主应力的最大与最小值相差小于3%，所以本文所提理论采用均匀分布表征拉伸试件弹性及塑性阶段的横截面应力-应变是较为合理的。

1.2 DIC 原理

DIC 技术本质是对一固定像素子区的图像数据在时间域内进行亚像素级别的高精度位移追踪。任选一个像素区域的中心作为目标点，DIC的核心理论在于精确追踪这个目标点所在像素块的形状变化过程，从而得到该目标点的位移时程数据。DIC 技术通过形函数对小区域像素块进行形状拟合，形函数可按阶数分为零阶、一阶、二阶形函数，阶数越高，对变形的拟合能力越强。目前DIC 主流核心算法为前向累加牛顿算法(Forward-additive Newton-Raphson, FA-NR)[8]和反向组合高斯牛顿(Inverse-compositional Gauss-Newton, IC-GN)[9]算法，上述算法通过亚像素迭代的方式，基于形函数精确拟合逼近得到像素块的量化形变过程。

硬件方面，采用经典DIC 试验架构进行金属拉伸试验[18]。

1.3 基于二阶链式子区的DIC 形变测试技术

本文基于DIC 原理实现链式形变测量，涉及全场DIC 测试。由于传统全场DIC 测试技术需要对全部成像区域的形变分布进行精细量测，多采用“小子区，多子区”量测理念，但这种测量方式无法适用于金属拉伸试验场景，也无法实现链式形变测量理论。因此，本文沿用“大子区，少子区”的量测理念，提出一种基于二阶链式子区的DIC 形变测试技术(Chain Subset based Secondorder DIC Deformation Measurement Technology,C-DIC)。

1.3.1 二阶链式子区

图2(a)为一金属试件拉伸试验的现场照片，通过DIC 图像处理可得到试件的形变结果。

图2 二阶链式子区Fig.2 Second-order chain subsets

首先需在图像内试件表面按一定规律布置DIC 子区。本文将所布设的子区命名为二阶链式子区，具体需要按照一定的方向，连续且紧密的布设多个具备较大尺寸的DIC 子区。布设子区前，需要先选取首子区与尾子区的中心点，也即首点(xa,ya)与尾点(xb,yb)，进而确立其余子区的中心点坐标。图2(b)中所有红点均为各个子区的中心点，若采用各个子区的局部形函归一化坐标，则可将各个子区的中心点坐标均表示为(0,0)。设子区个数为N，则各个子区的中心点坐标(xi,yi)为：

式中：(xa,ya)为首点坐标；(xb,yb)为尾点坐标；(xi,yi)为各个子区的中心点坐标，i∈[1,N]。

设各个子区的尺寸为宽W、高H，首尾点欧氏距离为L，则W可取为金属试件在图像内的像素宽度的80%及以上，不可大于金属试件像素宽度，H取为L/(N-1)。

可以看出，初始的链式子区生成阶段，需要确定首尾点以及子区个数N。首尾点一般选取为试件的平行长度段首尾中心处即可。N一般可取为30～50，N过大会造成子区内像素数据量过少，不足以运用DIC 进行迭代运算，N过小会导致子区高度过高，无法对颈缩处进行足够精确的DIC 形变追踪。图2(b)为采用N=40 生成的链式子区图像，图中圆点为各个链式子区的中心点。对于N的取值，假设试件平行长度段的像素尺度成像长度为Lpixel，可按区间N∈[Lpixel/20,Lpixel/25]来选取N的具体数值。N的不合理取值对C-DIC的影响如图3 所示，图3 为非合理子区个数N下的C-DIC 可视化处理结果对比。从图3 可以看出，当N=15 时，此时N取值过小，颈缩处附近的子区过大，无法合理描述颈缩处形变状态；当N=70 时，此时N取值过大，子区内图像纹理不充足，大形变区域(如颈缩处)的子区无法满足DIC 处理要求，自行退出计算。

图3 C-DIC 可视化结果对比Fig.3 Comparison of C-DIC visualization results

选用二阶形函数进行链式子区的DIC 运算，是为了适应试件在拉伸作用下可能产生的大幅非均匀形变(如颈缩处变形)。图2(c)为试件拉伸断裂前的最后一帧图像，图中框线为各个链式子区采用二阶形函数进行DIC 运算后的变形结果，从图中可直观看出，本文采用的是二阶链式子区可对试件各个区域的局部形变进行精确表征。

对每个生成的链式子区，采用二阶形函数进行DIC 运算，如图4(b)所示，其方程为：

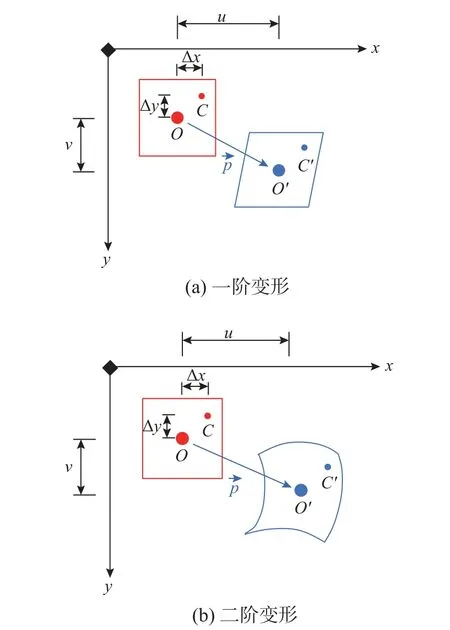
图4 形函数原理图Fig.4 Sketch map of shape function

式中：Δx与Δy表示点C(x,y)与点O(xo,yo)在x与y方向上的坐标差值；x′与y′为变形后任意点C的坐标；u与v为形变参数中的位移分量；ux、uy、vx、vy为u和v在相应坐标方向上的位移梯度；uxx、uxy、uyy、vxx、vxy、vyy为u和v在相应坐标方向上的位移二阶导数。

1.3.2 柔性链条逼近

对二阶链式子区进行DIC 运算后，可通过选取子区的角点，获得柔性链条的离散定量逼近，也即离散链。

通过图2 可以看出，各个子区存在四个角点。取断裂前最后一帧图像的链式子区测试结果，将各个子区角点绘制于图中，如图5(a)所示，图中各个相邻子区的角点采用不同颜色进行区分，在初始阶段，各个相邻子区的角点必然处于互相连接的状态，但从图5(a)可以看出：经过大幅变形追踪后，原本相连的角点，由于DIC 测试误差，互相产生了错位，越靠近颈缩处，这种错位现象越发显著。

图5 柔性双链逼近Fig.5 Approximation of flexible chain

将图5(a)的角点分为左右两侧，则每侧各2N个角点。为了对柔性双链进行离散逼近，同时为了增加测量精度，取相邻角点的坐标均值作为柔性链条的近似离散点，由此可得，每侧存在N+1 个柔性链条离散点，如图5(b)所示。此时每侧N+1 个离散点，共计2(N+1)个离散点，即为柔性链条逼近结果，本文将此类结果简称为离散链。

通过离散链数据，可对链式形变测量理论中的名义线应变 ε¯nom,t进行求解。设离散链存在N+1 个柔性链条离散点，将t时刻的离散链控制点集表示为Pi,t，i∈[1,N+1]，此时有：

式中：SL,0为初始离散链长度；SL,t为t时刻离散链长度；下标L、R 表示左链或右链；dj,L,t为t时刻第j段离散段长度，j∈[1,N]，算子dist 为两点欧氏距离； ε¯nom,t为t时刻名义线应变。

1.3.3 颈缩处极值点求解

采用本文的链式形变测量理论与方法，可对试件的颈缩效应进行量化，具体通过离散链曲线拟合和极值点求解来实现。

如图6 所示，设ypeak为离散点集内极值点的y坐标值，借助筛选极值的peak 算子，则有：

图6 颈缩处极值点Fig.6 Extreme point of necking area

设极值点对应的编号为ipeak，从ipeak两侧各选取两个点，组成五个离散点点集，并进行曲线拟合，则有：

式中：i为离散链点集Pi,t下标编号，此时i∈[ipeak-2,ipeak+2]；cubic 算子表示采用点集内的离散点坐标进行三次曲线最小二乘拟合；C 为三次曲线拟合参数。

图6(b)中的深色曲线为拟合得到的曲线结果。对于该三次曲线，可根据一阶导数为零进行极值点求解，得到的两个解中，取与极值点ipeak的x坐标距离最近的解作为颈缩处极值点x坐标值，代入三次曲线方程可求得y坐标值，由此可确定颈缩处极值点的位置，如图6(b)中的深色圆点所示。

设左链和右链的t时刻颈缩处极值点坐标分别为(yL,max,t,xL,max,t)和(yR,max,t,xR,max,t)，则两柔性链条之间的y方向最短间距Dpeak,t为：

1.3.4 颈缩处应变求解

通过离散链点集Pi,t，可将离散链应变分布表示为：

式中：j∈[1,N]；算子dist 为两点欧氏距离；下标L 或R 分别单独表示左链或右链，本式对左链与右链均单独成立。

从ipeak两侧各选取两个点，拟合得到颈缩处应变连续表达式：

式中：i为离散链点集Pi,t下标编号，此时i∈[ipeak-2,ipeak+2]；算子fit 代表拟合；x为横坐标。一般可采用三次曲线拟合。

进一步结合极值点坐标可得颈缩处应变为：

式中： εneck,t为颈缩处应变；下标L、R 表示左链或右链。

求解得到Dpeak,t与 εneck,t之后，可按链式形变测量理论进一步开展试件材性计算。

以上理论及方法采用C++编程实现，并基于大量实测数据进行验证及调试，实现了基于DIC 技术的金属材性自动测量。为便于实际应用，可在满足精度要求的前提下，对链式形变测量理论做一些合理假设，例如采用分段求和代替曲线积分、µt值取为泊松比或1 等。需要说明的是：µt取值不属于本文的研究范畴，简化起见，后文统一取µt=1。此外，为提高测量精度，还可基于链式子区中点形成中链，从而采用三条链的数据进行分析，相应计算方法相同，本文不再赘述。

2 试验设计

2.1 拉伸试件

根据《规范》设计了三组不同尺寸的矩形截面比例试样，按照拉伸段宽度分别命名为R15、R20、R25，如图7 所示。试件由Q460GJ 钢板切削加工而成，其含碳量适中，强度与塑性较好，在工程中使用广泛。每组包含3 个相同试件，每个试件的实测尺寸列于表1，表中符号的含义详见图7。

图7 拉伸试件示意图Fig.7 Dimension indicators of tensile specimen

2.2 测试方案

试验在MTS647 拉伸试验机上进行，采用准静态、匀速的位移控制加载方式，加载速率为1 mm/min，现场布置如图8 所示。图像采集方式为均匀时间间隔拍照，采用频率为1 Hz。需要说明的是，每帧图像与同时刻荷载需要一一对应。可以采用绝对时间或破坏点前溯的方法对图像与荷载进行匹配，或者将本文视觉测量系统与拉伸试验机进行软硬件融合开发，通过力反馈结果实时匹配图像并控制图像采样速率。

图8 试验布置Fig.8 Experiment setup

试验过程中，采用两台工业相机分别对试件的两个侧面进行拍摄测量。试件一侧采用喷漆进行散斑喷涂以提高DIC 测量精度，另一侧粘贴有同心圆标识物，便于采用传统图像识别方法对伸长率进行测量，如图8(b)～图8(c)所示。标识物由黑-白-黑三段同心圆构成，最大圆环直径分别为给定值，试件平行段的首尾处各贴一个同心圆标识物，通过识别算法精确追踪两个同心圆标识物在每一帧实测图像中的间距，从而得到试件受拉后各时刻伸长率。

对于R20 和R25 试件，在各自的2 号和3 号试件安装了引伸仪，用于与DIC 测量得到的弹性模量结果进行对比。引伸仪的标距为50 mm，同时为避免由于量程超限而导致引伸仪破坏，在材料屈服后立即将引伸仪拆除。

3 试验结果分析

3.1 拉伸断裂过程

拉伸试验破坏的重要特征在于试件在临近断裂时发生显著的颈缩效应。基于本文C-DIC 方法分别测得试件R20-2 颈缩部位与非颈缩部位断面宽度的变化曲线，如图9 所示，其中纵坐标采用变形后宽度与变形前初始宽度的比值。可以看出：

图9 试件横截面积时程曲线Fig.9 Time history curves of cross-sectional area quantification

1) 在线弹性阶段(0 s～80 s)，试件非颈缩部位与颈缩部位的宽度几乎不发生变化，横截面宽度仅减小了0.055%。

2) 在屈服阶段(80 s～104 s)，拉力荷载在很小的范围内波动，而试件的伸长量开始增加，横截面积开始减小。非颈缩部位与颈缩部位的横截面宽度仍保持近似相等，但与试验前相比分别减少了0.071%和0.072%。

3) 在强化阶段(104 s～470 s)，试件的塑性变形不断积累，可以明显地观察到整个试件横向尺寸的缩小。在强化阶段的前部分(130 s～300 s)，非颈缩部位与颈缩部位的横截宽度仍近似相等，试件可视为均匀伸长。在300 s 时刻对应的两处横截面的宽度分别减少了2.494%和2.541%，此时试件轴向应变为0.0724。在强化阶段的后部分(300 s～470 s)，由于颈缩区域的横截面应力更大，因此，颈缩区域面积与非颈缩区域面积之差逐渐增大。在470 s 时刻，拉力荷载达到最大，试件轴向应变为0.1425，非颈缩部位与颈缩部位的横截面宽度分别减少了5.370%和5.777%，实际尺寸相差0.08 mm。

4) 在颈缩阶段的前段(470 s～575 s)，颈缩部位与非颈缩部位的面积继续减小，颈缩部位的变化速率逐渐增大，非颈缩部位的宽度稳定于试验前的93%。在颈缩阶段的后段(575 s～716 s)，非颈缩部位面积基本保持不变，颈缩部位的面积急剧减小，颈缩部分的伸长约占总伸长量的90%，这是因为此时的拉力荷载减小，非颈缩区域能够抵抗进一步发生塑性变形，横截面积不再减小，而颈缩区域的塑性变形不断积累，横截面显著收缩，直至试件断裂。

3.2 弹性模量

基于本文C-DIC 测量结果，进一步结合试验机的拉力值，计算了拉伸试件的弹性模量，并与引伸仪的计算结果相对比，结果如表2 所示。

表2 弹性模量和极限伸长率的测量结果Table 2 Comparison of extensometer, artificial target and C-DIC results

由于实际拉伸试验的初始阶段存在诸多不稳定因素，一般通过一段应力区间内的应变进行弹性模量计算。本文计算弹性模量的应力范围取为100 MPa～300 MPa。对比发现：与引伸仪结果相比，C-DIC 测量得到的弹性模量最大相对误差为2.83%，可见，本文C-DIC 方法对于弹性模量的测量精度是可靠的。

3.3 极限伸长率

基于试件断裂前的最后一张图片，采用本文C-DIC 方法及标识物方法测量得到试件断裂破坏前的极限伸长率，两种方法进行比较，可以进一步验证本文C-DIC 方法的有效性。

从表2 数据可以看出，C-DIC 相比于标识物测量的相对误差均在3%以内，说明本文C-DIC方法对于大形变场景下的测量是有效的。考虑实际测试场景，标识物所覆盖的试件表面会随荷载增加而发生形变，然而标识物本身不会发生形变，这就导致了标识物与试件表面存在滑移，从而产生测量误差。虽然同属视觉测量方法，本文C-DIC 方法相较于基于标识物的传统计算机视觉识别方法更为合理有效。

3.4 真实应力-应变曲线

图10 为试件R20-1 的完整应力-应变曲线测量结果。图中共计存在三条曲线，“标识物(名义应力)”为不考虑截面收缩率的情况下，通过标识物结果计算得到的应力-应变曲线；“标识物(体积不变原则)”为基于标识物的伸长率测量结果，基于体积不变原则[20,24-25]对截面面积进行线性修正后，所计算得到的应力-应变曲线；“C-DIC(颈缩处应力)”为本文C-DIC 方法计算得到的颈缩处应力-应变曲线。“标识物(体积不变原则)”曲线的应力是根据通用的体积不变原则公式全程计算得到的，该式为：

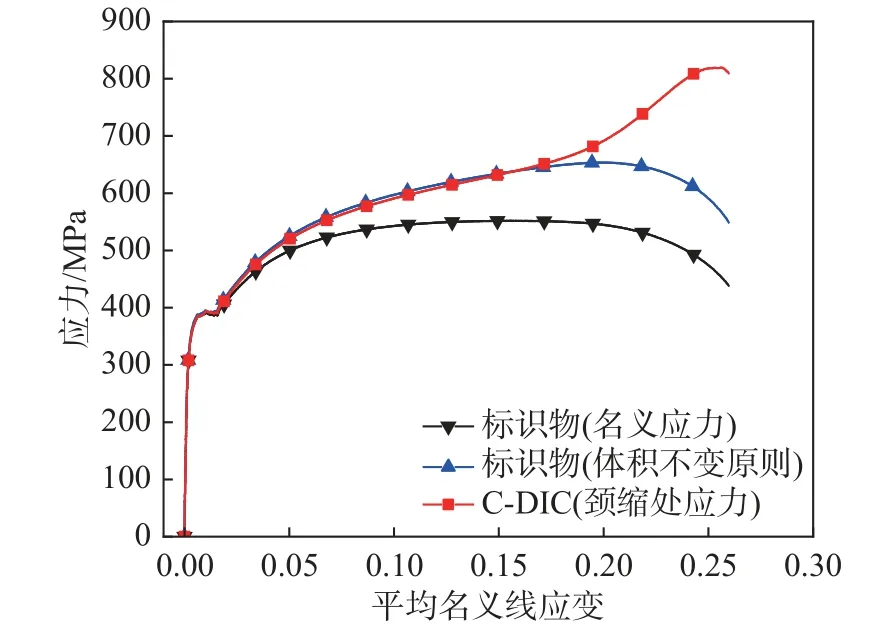
图10 应力-应变曲线对比图Fig.10 Comparison diagram of stress-strain curves

式中： σnom与 εnom为传统的名义应力与名义应变；σvc为体积不变原则下的轴拉应力。

可以看到，在线弹性阶段，三种方法计算的应力之差小于0.5 MPa。在屈服阶段，试件的应力在小范围内波动，应变大幅增加，但两种方法计算的应力基本相等；在强化阶段，“标识物(体积不变原则)”与“C-DIC(颈缩处应力)”的应力-应变曲线基本重合，但前者应力值略大于后者，两种方法计算得到的应力相差最大为6.13 MPa，相对误差1.0%。

随着试件继续被拉伸，尽管拉力呈现减小的趋势，但颈缩部位的横截面积急剧减小，颈缩部位的应力仍继续增加，在达到峰值819.01 MPa 后试件发生断裂。采用体积不变原则计算的应力最大值仅为653.57 MPa，未能反映这一特点。

将本文C-DIC 方法测得的试件R20-1 颈缩处的完整应力-应变曲线绘制于图11 可以看出，颈缩处的实际应变为0.925，远大于名义线应变0.260，这反映出了材料的真实特性，体现了本文C-DIC方法的优势所在。

图11 颈缩处应力-应变曲线对比图Fig.11 Stress-strain curve of necking area

4 结论

本文针对金属拉伸试验场景，提出了链式形变测量理论与C-DIC 方法，该方法通过DIC 二阶链式子区、分段离散、极值点求解等步骤，实现了链式形变测量理论，可自动化测量弹模、颈缩量、伸长量、真实应力-应变曲线等金属材性指标。具体结论如下：

(1) 采用C-DIC 进行了多组标准金属试件的拉伸试验，本文方法测得的弹性模量、极限伸长率与传统测量方法对比，误差小于3%。

(2) 通过颈缩量、颈缩处应力-应变曲线与体积不变原则所得曲线等测量结果的对照分析，进一步验证了该方法的有效性。

(3) 与传统金属拉伸试验方法相比，本文方法在测量精度、效率及成本等方面均具有显著优势，可在实验室内推广应用。