基于知识图谱推理的热轧带钢产品质量缺陷追溯
张佳琪,凌卫青
(同济大学 电子与信息工程学院CIMS研究中心,上海 201804)
0 引言
钢铁工业是国民经济发展的支撑,也是国家的基础工业之一。热轧带钢是指通过热轧方式生产的带材和板材,广泛用于汽车、电机、化工、造船等行业。在我国制造业高质量发展政策指引下,汽车制造、船舶制造、基础设施工程等领域的产品研发迭代加速,对热轧带钢钢种及品质需求日趋个性化,推动带钢生产朝着“小批量、定制化”方向发展。
钢铁产品的质量管控主要包括:接受订单开始的钢品性能质量设计、生产过程中在线质量监测以及产成阶段的质量分析及工艺改进[1]。热轧带钢生产需要经过加热炉、粗轧机组、飞剪、精轧机组、层流冷却、卷取机组等多个关联耦合的复杂工序,并且各个工序内部也存在许多相互关联耦合的子工序,全流程中众多的过程变量与控制回路互联耦合,生产过程中参数的变动最终都将影响出口段的带钢产品质量[2]。面对复杂化的带钢生产过程,产品质量分析至关重要。其中,产品质量缺陷追溯着眼于探寻导致质量缺陷的关键工艺参数,可以辅助优化工艺参数、提高生产稳定性和可靠性、减少新品试车次数。
传统质量异常溯源主要针对某一工况或工序进行建模,采用统计学方法,通过多元统计分析实现产品质量监测,再结合格兰杰因果关系或者传递熵等方法来揭示变量间的关联关系[3]。然而,在大规模、动态、高维参数的复杂生产控制环境下,带钢轧制随着物料流、能量流的传播扩散,历史工序偏差传播以及多工序综合影响都将导致带钢质量异常。随着传感技术、通信技术和人工智能的快速发展,一些学者开始尝试数据驱动的方法(例如深度学习、集成学习等),利用人工智能技术解决各个工序间信息孤立的问题,实现质量缺陷溯源,提高产品质量的稳定性和可靠性[4-5]。但限于深度学习模型的黑盒特性,导致在预测结果偏离目标时,对质量偏差原因的追溯十分困难。
在实际带钢轧制过程中,专家需要统筹考虑各个生产过程控制层,结合专业机理知识、具体的设备物料信息,同时凭借自身经验完成对产品质量的分析与优化。面对大量不同生产批次以及设备工况动态变化,人工决策优化的方式无法做到快速响应,同时也无法对每一个生产批次进行准确分析,导致经验知识的缺失。在生产数据中隐含丰富的数据语义信息,通过数据挖掘方法可以获取生产数据间存在的关联性,但对可靠性要求高并且隐含语义信息的获取难度大[6]。因此需要人工智能、知识图谱等技术有效结合工艺机理、专家经验和数据挖掘结果等知识,辅助指导生产控制决策。
基于上述分析,本文将可解释人工智能技术应用于带钢热轧质量数据挖掘,并结合生产过程机理与专家经验构建带钢质量知识图谱,在此基础上设计一种将知识图谱映射到贝叶斯网络的方法,通过贝叶斯推理挖掘产品质量缺陷因素,并通过某钢铁公司热轧带钢精轧生产实际数据,验证本文提出方法的科学性和有效性。
1 相关研究工作
1.1 质量分析
热轧带钢质量分析研究从目标上主要包括:质量监控、溯源和预测。
质量监控大多基于多元统计分析理论,通过建模正常生产工况数据的控制上下限来实现对生产状况的监控[7-8],并将其应用于产品质量的分析中,包括潜在结构投影[9]、典型相关分析结合堆叠自编码器[10]等。同时结合格兰杰因果关系或传递熵等方法,通过建立因果矩阵或因果拓扑图,挖掘变量间的因果关联,实现异常原因追溯。但上述方法大多针对某一工况或工序进行建模分析,存在复杂工序追溯困难的问题。
随着日益增长的数据量,以深度学习和集成学习为主的机器学习方法广泛应用于设备监控[11]、质量预测[12]等方面。该方法从大量生产历史数据中发现工艺参数和质量参数之间的相关性,进而实现对质量参数的预测。LEE等[13]将卷积神经网络(Convolutional Neural Network,CNN)和递归神经网络(Recurrent Neural Network, RNN)相结合来处理空间和时间序列信息,实现对炼钢连铸过程温度分布的预测。LI等[14]使用卷积神经网络实现对热轧带钢抗拉强度的预测。WANG[15]将随机森林应用于钢包炉中钢水温度的预测,随机森林算法通过Bootstrap重采样技术为每棵决策树生成训练样本,同时随机选择训练样本中的特征进行分裂。因此具有良好抗噪声能力,同时可以有效处理高维特征,不需要进行特征选择,并且随着决策树增加,模型的泛化误差存在上界,不会出现过拟合[16]。
目前,基于机器学习的质量预测模型能达到较高性能,但随着模型复杂度不断上升,导致专家无法理解模型作出预测的行为(尤其是与专家判断不一致时),难以直接采用模型进行生产决策。机器学习模型的可解释性受到关注,于是出现了可解释人工智能(eXplainable Artificial Intelligence, XAI)方法,如LIME[17]和SHAP[18]。XAI通过解释模型预测的行为,提高模型的透明度与可靠性,并获取隐含在数据中的语义信息。TAKALO-MATTILA等[19]基于梯度增强树建立钢板表面缺陷的预测模型,并使用SHAP方法寻找工艺参数与表面缺陷之间的潜在关联,以特征贡献的大小给出模型预测行为的局部解释。SHAP是一种模型事后解释方法,被证明是分配特征重要性的唯一方法[18],意味着将预测模型视为一个“黑匣子”,实现在不影响模型决策精度的情况下提供相应的决策结果解释。
1.2 工业知识图谱
知识图谱(Knowledge Graph,KG)是大数据时代的一种重要的知识形式化表达方法,目前在许多领域得到了广泛应用。相较于Google知识图谱为代表的通用知识图谱,工业知识图谱知识深度更深,知识细粒度要求更高,对知识的准确性要求严苛,通常被应用于决策任务中。ZHOU等[20]设计了石油化工生产过程仿真的本体,并在此基础上构建了柴油生产知识图谱,使生物柴油生产工艺可在不同市场状况下获得最佳运行条件,降低能耗,实现工厂利润最大化。MAO等[21]运用知识图谱的推理分析能力发现过程制造中紧急情况下可能的风险原因和后果之间的隐藏关系。CHEN等[22]针对冷滚轧生产过程的钢带断裂问题,从多个数据源中提取了相关特征并构建了知识图谱,并应用嵌入技术实现了钢带断裂的建模。牟昊天等[23]提出面向流程工业控制系统的知识图谱构建的一般性方法框架,实现对信息物理资产的管理。
知识图谱是融合不同来源知识的有效方法。当下以流程工业质量控制决策为应用背景的知识图谱相关工作比较少,且大多将知识图谱视为知识库,通过知识检索,查找所有潜在原因,利用知识图谱推理进行质量缺陷原因追溯的分析方法研究十分欠缺。因此,本文利用工业知识图谱将工艺机理、专家经验以及可解释数据挖掘结果等知识进行融合,在此基础上通过知识图谱推理实现对质量缺陷原因的追溯。
2 研究方法
2.1 整体架构
本文研究基于知识图谱的热轧带钢产品质量缺陷追溯,因此需要获取带钢生产中存在的显性以及隐性的知识构建知识图谱,并运用知识图谱实现对产品质量缺陷追溯,整体架构如图1所示。
生产数据中包含大量隐性的知识,市场需求变化导致不同生产批次物料成分、工况的变动,使工艺参数与质量参数之间的关联强弱也在动态变化。本文通过SHAP方法,对建立的随机森林质量预测模型进行事后解释,计算不同工艺参数对质量预测结果的贡献,其中对质量预测结果贡献大的工艺参数与质量参数之间存在关联,需要以三元组的形式持久化在图数据库,如图2所示。本文中知识图谱采用自顶向下和自底向上相结合的方式构建。首先通过工艺机理构建知识图谱模式层,其中工艺机理从工艺标准、技术文档等资料中获取信息,以反映原料种类、产品质量规范和生产工艺流程。其次采用自底向上的方式,从企业会议记录以及产品质量分析报告等非结构化数据源中获取反映专家对生产中工艺参数同质量之间关联的经验知识,补充到图谱数据层。但面对大量历史生产数据,专家无法对每一个生产批次进行分析判断,因此需要通过上述数据挖掘技术发现隐含在生产数据中工艺参数与质量参数之间的关联,选择其中置信度较高的信息,加入到知识图谱中。

图2 质量分析知识图谱结构示意图
在工业领域中知识图谱侧重于辅助生产决策。上述构建图谱中主要包括工况信息、物料信息、设备信息以及工艺参数和质量参数之间关联,因此可以将图谱应用于产品质量缺陷追溯,分析导致质量缺陷的工艺参数。在带钢轧制中,需要根据不同的物料信息(如厚度、温度、化学成分等)对精轧机组的负荷进行分配,计算机控制系统则需要根据精轧机组的负荷进一步计算各个机组的工艺参数。不同物料信息导致精轧机组工况不同,设定的工艺参数之间也存在差异。因此,在对某一次生产的质量缺陷进行追溯时,需要获取与当前生产中物料信息和工况信息相同或者相似的历史生产信息所构建的子图。通过将子图中的工艺参数实体、质量参数实体以及工艺参数实体与质量参数实体之间的关系映射到贝叶斯网络实现对网络结构的获取。工艺参数实体、质量参数实体中使用属性记录的工艺参数与质量参数的实际值,通过离散化算法来获取贝叶斯网络参数学习所需数据,并确定网络中各个变量的概率分布。最终将生产的工艺参数和质量参数作为贝叶斯网络中的已知变量,推断出不同工艺参数和质量参数间关联存在的后验概率,实现对质量缺陷的追溯。
2.2 基于XAI的数据挖掘
热轧带钢的质量主要取决于精轧段中各个精轧机组,其中影响带钢质量的工艺参数包括轧制力、压下位置、入口温度、水流量和机架速度等。出口段质量的评估主要从尺寸、力学性能以及板型进行分析,如表1所示。每一个生产批次中的精轧机组工艺参数、入口段工艺参数以及出口段质量参数构成单个样本。

表1 带钢质量指标
针对不同质量指标,以厚度y为例,数据挖掘任务首先需要建立以精轧机组工艺参数和入口段工艺参数(如入口温度、入口厚度等)为特征x的质量预测模型,本文通过随机森林算法建立产品质量缺陷的预测模型。随机森林属于集成模型,通过组合多个决策树,使总体准确度优于集合中的任何单个决策树。模型φ通过聚合函数G来聚合不同决策树fi以实现对单个样本的预测,公式如下:
(1)
实现对产品质量缺陷预测后,通过SHAP获取模型φ对单个样本预测相应的解释,即局部解释,以特征归因的形式获取模型预测行为中不同工艺参数的贡献,进而获取导致质量偏差的关键工艺参数。对单个样本x的局部解释公式如下:
(2)
式中:g为解释模型,m为样本特征的维度,φ0(φ,x)=E[φ(X)]表示模型在训练数据集X中的预测期望值,φi(φ,x)为解释模型对特征xi的归因值(Shapley值)。每个特征Shapley值计算公式如下:

(3)
其中S为解释模型所使用的特征子集。每一个特征的Shapley值描述该特征导致带钢产品缺陷的贡献,在特征集F={x1,…,xm}中选择贡献较大的特征,作为导致质量缺陷的关键工艺参数,将其持久化到知识图谱,最终选择的特征子集Fsub为:

(4)
其中M=max{φj|xj∈F}为所有特征中的最大Shapley值,k和n是超参数,k限制集合中特征的最小Shapley值,n限制集合的大小。
2.3 基于知识图谱推理的质量缺陷追溯
知识图谱的结构示意图如图2所示,实体通过属性包含许多生产信息。实体b包含每个生产批次的基本信息(如带钢号、段号等),构成集合B;实体p包含某一工序下的多个工艺参数(如精轧机组工序的轧制力、压下位置等工艺参数),构成集合P;实体q中包含产品质量信息,构成集合Q;实体c包含生产中不同工况信息、物料信息(如钢种、厚度级等)需要与实体b进行关联,构成集合C。同时,每一个生产批次中的实体p和实体q之间存在各种类型的关系r,通过关系的来源(如专家或SHAP)以及对实体q产生影响的具体工艺参数类型来区分,表示某一工序中某个工艺参数导致质量缺陷,构成集合R。
质量缺陷的追溯通过将知识图谱子图映射为贝叶斯网络,实现对生产中工艺参数与质量参数之间不确定关系的分析。贝叶斯网络通过有向无环图(Directed Acyclic Graph,DAG)表示一组变量及其条件依赖关系,适合用于从已有的观测中推断出可能的原因。定义贝叶斯网络BN=(GBN,θ),其中GBN=(EBN,RBN)表示DAG结构,EBN表示变量集,RBN表示有向边集,θ表示变量间的条件概率表。针对某一次生产的输入信息x:
x=(xC,xP,xQ)。
(5)
式中:xC表示工况信息、物料信息对应于图谱中实体c,xP为工艺参数对应于图谱中实体p,xQ为质量参数对应于图谱中实体q。
首先,实际生产中根据订单中产品尺寸以及性能需求明确厚度级、温度级、钢种等工况和物料信息后,计算机控制系统需要依次计算每台轧机的负荷、轧制速度以及其他工艺参数,因此工作在不同工况下轧机的工艺参数存在明显差异。文中将厚度级、温度级、钢种等作为子图抽取的依据,从图谱中抽取部分实体b以及同实体b存在关联的实体p和实体q所构成的子图Gsub:
Gsub=(Bsub,Psub,Qsub,Rsub)。
(6)
其中Bsub⊆B,Psub⊆P,Qsub⊆Q,Rsub⊆R,集合Bsub中每个实体在原图谱中关联的实体c的信息同xC一致或者相似。
在将子图映射到贝叶斯网络过程中,分为变量集EBN映射、有向边集RBN映射两个步骤。
(1)变量集EBN映射 贝叶斯网络中存在两种类型的节点变量:可观测变量和潜在变量。可观测变量包括生产中可测量的工艺参数变量以及最终检测到的质量参数变量;潜在变量是无法观测的变量,表示生产中潜在的导致质量缺陷的原因或参数。因此映射公式如下:
f:Pprop∪Qprop∪Rsub→EBN。
(7)
其中Pprop为Psub中属性构成工艺参数变量集合;Qprop为Qsub中属性构成的质量参数变量集合,f表示映射法则,将Pprop和Qprop映射为贝叶斯网络中的可观测变量集,将不同类型的Rsub映射为潜在变量集。
(2)有向边集RB映射 对Rsub中所有元素r:建立从r在子图中对应头实体p映射的工艺变量到r映射的潜在变量的有向边;建立从r映射的潜在变量到r在子图中对应尾实体q映射的质量变量之间的有向边。

(8)
(9)
其中:N表示总样本数,S表示质量缺陷类别数,m表示工艺参数划分间隔数,Ni+表示第i类质量缺陷样本总数,N+r表示工艺参数在区间(dr-1,dr]的样本总数,qir表示工艺参数在区间(dr-1,dr]的类别为i的样本总数。在训练数据D中使用极大似然估计获取θ:
(10)
其中L(θ|D)=P(D|θ)是在给定θ后的条件概率,用使L(θ|D)最大化的θ*估计θ。最终将xP和xQ分别作为贝叶斯网络中工艺参数变量EP和质量参数变量EQ的输入,估计各个潜在变量EPo导致质量缺陷的后验概率p:
p=P(EPo|EP=xP,EQ=xQ)。
(11)
3 案例验证
3.1 数据来源
数据来自于某钢铁公司热轧带钢精轧段生产线,如图3所示共包括7台精轧机,分别为F1~F7。出口段设有带钢质量的检测仪表,可实时监测轧件的厚度、温度等质量参数,采集了8天内精轧段7个精轧机的计算机控制系统设定的工艺参数和F7出口处传感器检测到的带钢质量参数,共8484组数据。表2给出精轧机组部分工艺参数及其数据库中对应英文字段的示例,机架号表示产线中机组的位置(如压下位置_1或SCREW_DOWN_1表示第一台精轧机组的压下位置)。同时将精轧入口温度(数据库中英文字段:FM_ENTRY_TEMP)也作为预测模型的输入特征。

表2 精轧机组工艺参数示例

图3 带钢热连轧精轧段
带钢质量指标如表1所示。其中力学性能以当下传感技术难以在生产中直接检测。精轧过程中要求控制出口终轧温度在一定范围内,通常在带钢经过层流冷却和卷取机成卷后进行采样检测,实际生产中专家主要通过出口温度判断带钢力学性能[25]。终轧温度太低将使带钢力学性能下降,太高可能导致表面二次氧化[26],因此实验中使用出口终轧温度近似力学性能的预测。最后将出口厚度和出口温度作为质量指标,分别对出口厚度和出口温度进行标记,在规定的最小值与最大值之间为正样本,低于规定的最小值为负样本一,高于规定的最大值为负样本二,标记后的实验数据集如表3和表4所示。

表3 出口厚度数据集

表4 出口温度数据集
3.2 数据知识挖掘
根据式(1)使用随机森林算法分别建立出口厚度和出口温度的预测模型,从表3表4中看出两个质量指标的正负样本之间不平衡比较严重,导致模型对负样本的分类性能下降,难以获取有效的模型。模型分类的精度也会很大程度影响事后解释方法的效果。实验中使用过采样算法Borderline-SMOTE[27]平衡正负样本,并通过网格搜索法从一组指定的参数中选择随机森林算法最优超参数,表5和表6中给出超参数搜索结果。最终采用特异度(specificity)、灵敏度(sensitivity)和G-mean作为评价指标。特异度评价负样本分类的正确率。灵敏度也称召回率,评价正样本分类的正确率。G-mean作为一个评价正样本正确率和负样本正确率的综合指标。表7和表8展示了表5和表6给定的超参数下模型分类的结果。

表5 厚度模型参数

表6 出口温度模型超参数

表7 出口厚度分类模型结果

表8 出口温度分类模型结果
通过式(3)计算出口厚度与出口温度预测模型中每一个样本的Shapley值,并用于分析工艺参数与质量参数之间关系,图4给出了厚度与出口温度模型中特征重要度最大的前6个特征,以及它们对模型输出的影响,红色代表较高的特征值,蓝色代表较低的特征值。例如,图4aTORQUE_6中较高的特征值(红紫色散点)的Shapley值偏低,表明较高的F6的力矩可能与厚度低于规定的最小值有关;图4b FM_ENTRY_TEMP中较低的特征值(蓝色散点)的Shapley值偏低,表明较低的入口温度可能导致出口温度低于规定的最小值。

图4 特征贡献摘要图
模型预测的正确性很大程度上影响Shapley可靠性,实验中设定阈值p,采纳模型预测概率大于阈值的解释,并且依据式(4)将特征子集中的工艺参数作为影响质量参数的原因补充到知识图谱中或者与已有的相关实体进行关联,如图5所示。图5左侧黄色实体类型为过程参数通过属性记录不同精轧机的工艺参数,红色实体类型为质量参数,绿色实体类型为每个生产批次的ID通过带钢号和段号区分。过程参数和质量参数之间关联的差异通过不同类型属性边来区别不同工艺参数的影响。例如图中带钢号为216241511500的批次中,SHAP给出精轧机组F7的速度导致出口温度低于规定的最小值;带钢号为216257202500的批次中,SHAP给出精轧机组F6的压下位置导致出口厚度低于规定的最小值。

图5 质量分析知识图谱
3.3 质量缺陷追溯
实验中将数据挖掘结果中80%的样本持久化到知识图谱中,20%的样本作为验证集。在对验证集每一个样本进行质量追溯时,首先使用物料信息(钢种家族代码中分类、钢种家族代码小分类)、工况信息(温度级、厚度级)通过式(6)抽取子图,其中企业中规定钢种家族代码中分类对带钢化学成分进行初次划分,小分类则进行更细致划分,厚度级和温度级是出口厚度和出口温度的规范。然后,依据式(7)完成贝叶斯网络结构映射,将子图中实体属性包含的工艺参数利用CACC算法进行离散化,并通过极大似然估计实现对贝叶斯网络的参数学习,将工艺参数与质量参数作为输入,预测贝叶斯网络中不同潜在变量的后验概率。潜在变量对应图谱中不同类型的关系,于是问题转化为对工艺参数和质量参数之间缺失关系进行预测,因此使用平均倒数排名(MRR)、Hits@n(Hits@1、Hits@3、Hits@10)作为评价指标。MRR用来衡量正确的潜在变量在所有候选潜在变量中排名倒数的平均值,该评价指标越高,表明正确的潜在变量在候选潜在变量列表中的排名越靠前,模型预测越准确。Hits@n用来衡量正确的潜在变量排名前n位的概率,该指标越高,表明效果越好。
(12)
(13)
同时实验中需要依次确定阈值p以及式(4)中的比例系数k,特征子集限制因子n三个参数,通过调整3个参数的取值使评价指标MRR最大化。其中参数p是在采纳解释时设定的模型预测概率阈值,当模型预测概率较高时才能保证解释的可信性;参数k是比例系数,保证最终选择的特征子集中的工艺参数对预测模型输出具有较大影响;限制因子n的作用是限制特征子集大小。实验结果如图6所示,结果表明p=0.65,k=1.5,n=2时,评价指标MRR最大化。

图6 参数确定实验结果
下面给出验证集中一个案例,各个精轧机组工艺参数见表9,精轧入口温度为966.25℃,出口厚度为3.00mm, 出口温度为888.2℃, 其中出口温度低于规定的最小值。子图抽取中给出9个潜在变量,如表10所示。最终对各个潜在变量导致质量缺陷的概率进行预测,得出精轧机组F3的轧制速度导致出口温度低于规定的最小值。同时此案例中被标记的导致质量缺陷的工艺参数为精轧机组F3的轧制速度,其在所有潜在变量预测概率中排名为1。
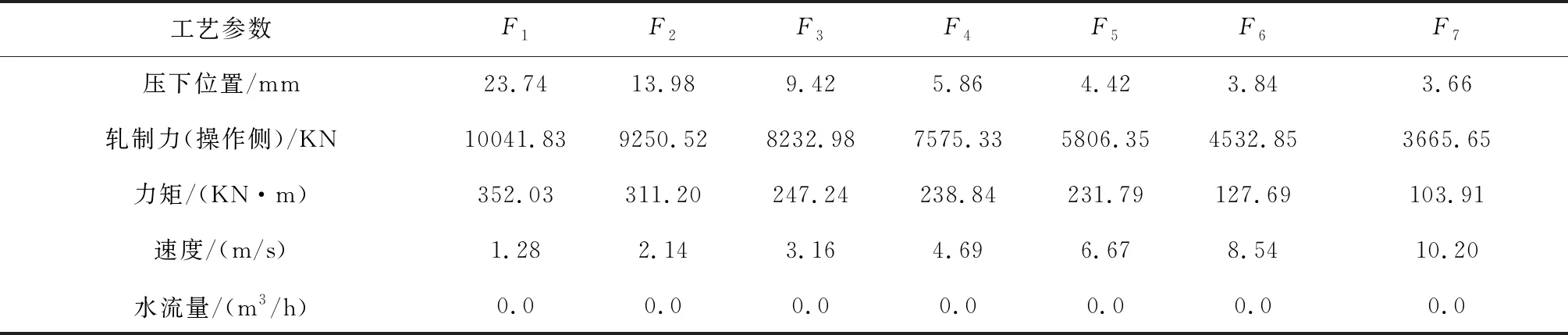
表9 精轧机组工艺参数

表10 预测概率
最终在整个验证集中进行了实验,得出每个样本中标记的导致质量缺陷的工艺参数在所有潜在变量中的排名并计算评价指标,结果如表11所示。通过Hits@3指标可以看出,在验证集中标注的导致质量缺陷的工艺参数,大部分都能被模型准确地识别。

表11 质量分析结果
4 结束语
针对热轧带钢生产过程机理复杂、工序关联关系耦合、工艺参数繁多等问题,本文采用可解释人工智能方法实现数据挖掘,通过知识图谱有效融合生产中存在的工艺机理、专家经验以及数据挖掘结果等知识,并将知识图谱的结构信息和生产信息映射到贝叶斯网络,实现对导致热轧带钢质量缺陷的关键工艺参数的识别。最终,对实际生产数据中200个存在质量缺陷的批次进行验证,结果显示,对于大部分导致质量缺陷工艺参数具有较好识别率。
需要指出的是,数据挖掘的可靠性十分重要。同一批次数据中,数据挖掘结果和不同专家的分析结果可能有偏差,这些结果最终被采纳的概率也不相同。知识图谱中存在许多三元组来源于SHAP对预测模型的解释结果,在不同批次数据下,随机森林模型对预测结果给出的概率存在差异,导致解释结果可信度不相同。本文在对质量缺陷追溯获取关键工艺参数的过程中,没有考虑到不同三元组的可信度,未来的研究将结合知识图谱中不同知识来源的可信度,进一步提高质量缺陷追溯的识别率和可信度。

