稻谷薄层红外干燥特性及数学模型
尹晓峰,杨 玲
(重庆商务职业学院1,重庆 401331)
(西南大学工程技术学院2,重庆 400715)
稻谷作为全世界主要的粮食产物[1-3],其产量和品质对人类健康有着深远的影响。但由于我国农业现代化还不够发达,大部分农民在收获稻谷后,只是对其进行传统的晾晒[4-7],不但耗时长、而且晾晒后的品质得不到保证。如果未对收获后的稻谷进行有效干燥或干燥后达不到干燥安全水分,会使稻谷中多种生物酶的活性达不到有效抑制,导致稻谷霉变而不能食用。
红外干燥是根据稻谷内部分子吸收红外线的特性,把作用在分子上的红外辐射能转变为热能,进而促使分子内部水分汽化,达到烘干目的。相比于其他干燥,红外干燥具有干燥速率快、干燥能耗低、干燥后稻谷质量好,且具有在稻谷干燥过程中不需要加热介质,稻谷内外能够均匀受热等特点,受到广泛关注[8-11]。目前,稻谷干燥形式以热风干燥工艺为主,其他干燥工艺为辅。尹晓峰等[12]对稻谷进行了热风干燥,发现热风温度是影响稻谷干燥的最显著因素。袁建等[13]在稻谷水分迁移状况、品质等不同条件下,通过对稻谷进行微波干燥发现,采用1.29 W/g微波剂量和60 ℃温度为最佳微波干燥工艺方案。李栋等[14]通过低温干燥方法对水稻进行了干燥,并建立了干燥数学模型,发现实验实测值和模型值差值较小。Ondier 等[15]通过对稻谷进行干燥后发现,干燥温度是影响稻谷干燥后品质的最重要因素。Ambardekar 等[16]主要研究干燥时间和干燥温度对稻谷干燥后品质的影响。Patindol等[17]设计出一款热对流与太阳能复合干燥机,提升了稻谷干燥工艺的效率。Gujral 等[18]指出,对稻谷进行多次干燥与连续干燥相比,稻谷每小时失水率提升0.5%。
实验主要通过正交实验方法对稻谷进行红外干燥,研究了稻谷分别在不同含水率、干燥温度和装载量干燥条件下的红外干燥特性。对实验结果进行极差和方差分析,找出稻谷最优红外干燥工艺方案。为进一步降低爆腰率,将实验后的样品进行缓苏实验,分析缓苏温度和缓苏时间对样品爆腰率的影响。根据国内外提出的多种干燥数学模型,找出稻谷最优红外干燥数学模型。稻谷在红外干燥过程中,计算其有效水分扩散系数和活化能,为日后更深入地研究稻谷干燥工艺提供参考。
1 实验设计
1.1 实验材料
选购品质较好稻谷种子作为研究对象,并对其进行挑选,选出颗粒均匀、饱满、无裂痕,未发芽的种子。
1.2 实验仪器
小型红外干燥实验台,小型恒温恒湿电热干燥箱,节能小型冰柜,AL204 型电子天平等。
1.3 参数指标
1.3.1 样品初始含水率、水分比的计算
应用GB/T 14489.1—2008《油料水分及挥发物含量测定》[19]方法来计算实验对象的初始含水率,采用人工加湿法[20]使实验对象达到实验要求的含水率水平(见表1),在实验前期,测出稻谷种子的初始含水率。其水分比见式(1)。
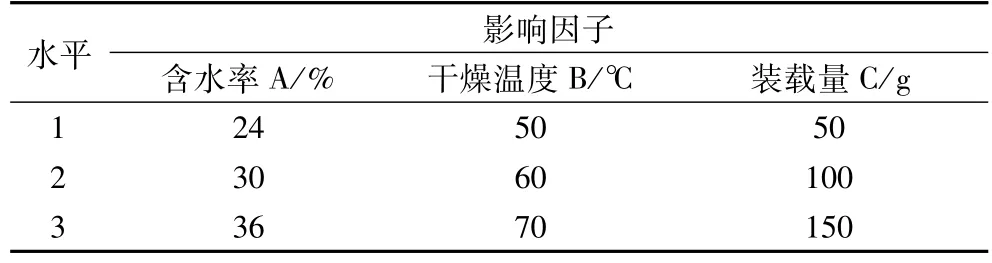
表1 正交实验因子与水平
式中:MR为样品的水分比;M0为样品的初始水质量分数/%;Me为样品的平衡水质量分数/%;M为样品在某一时刻的含水率/%。
样品在进行红外干燥时,因为干燥温度过高,会导致样品的Me很低,且可忽略不计。因此,样品水分比可以近似用式(2)代替计算。
1.3.2 样品干燥速率、有效水分扩散系数和活化能的计算
样品干燥速率、有效水分扩散系数和活化能的计算见式(3)~式(5)。
式中:V0为干燥速率/% /min;M1为样品的初始含水率/%;Δt 为干燥时间/min;MR 为样品的水分比;Mt为样品在干某一时刻的含水率/%;L为样品铺料厚度的一半/m;Deff为样品的有效水分扩散系数/m2/s;Ea为样品的活化能/kJ/mol;T 为绝对温度/K;R为气体常数/kJ/(mol·K);D0为Arrhenius 方程指数前因子/m2/s。以lnMR 为因变量,t 为自变量,绘制式(4)的曲线,并对曲线进行线性拟合,根据直线的斜率可计算出。以lnDeff为因变量,1/T 为自变量,绘制式(5)的曲线,并对曲线进行线性拟合,根据直线的斜率可计算出。
1.3.3 干燥数学模型的评价
从多种常见干燥数学模型中选取10 种干燥数学模型,找出稻谷最优红外干燥数学模型,并对实验数据和模型数据进行拟合验证。把相关系数(R2)、卡方(χ2)、均方根误差(RMSE)3 个指标作为评价数学模型质量的标准,其中,相关系数越大,卡方越小,均方根误差越小,证明数学模型的拟合度越好[23]。各指标的计算公式见式(6)~式(8)。
式中:MRexp,i为样品在实验中第i个数据点的实验值;MRpre,i为样品在实验中第i个数据点的预测值;n为数学模型中参数的个数;N为实验中数据点的数量。
1.3.4 样品爆腰率的测定
将实验样品均匀平铺在干净、方正、平整的玻璃台上,随机选取100 粒稻谷,用聚光手电筒观察100粒稻谷有裂纹的颗粒数,其中,爆腰率计算公式为:爆腰率=样品有裂纹的数目/100 粒样品的数目[24]。
1.4 实验方法
1.4.1 红外干燥实验
在稻谷进行红外干燥前,将预湿处理后的样品根据实验要求均匀平铺在实验托盘上,称出样品和托盘的总质量。红外干燥实验以含水率、干燥温度和装载量作为变量因子,采用L9(34)水平正交实验研究各影响因子对样品有效水分扩散系数和爆腰率的影响程度,见表1 和表2。实验中,每间隔5 min将稻谷和托盘进行称量,单位精确到0.01 g,直到样品达到国家规定的安全含水率为止。在样品进行红外干燥时,如果选出的干燥温度过低,则干燥速率较慢,干燥时间较长;但如果干燥温度过高,则样品干燥后爆腰率过高导致品质较差,不能满足实际需求。因此,经过查阅文献[25-27],选定实验干燥温度50、60、70 ℃3个水平。样品进行完红外干燥后,将干燥后的样品装进密封的小瓶中,24 h后,测定其爆腰率。
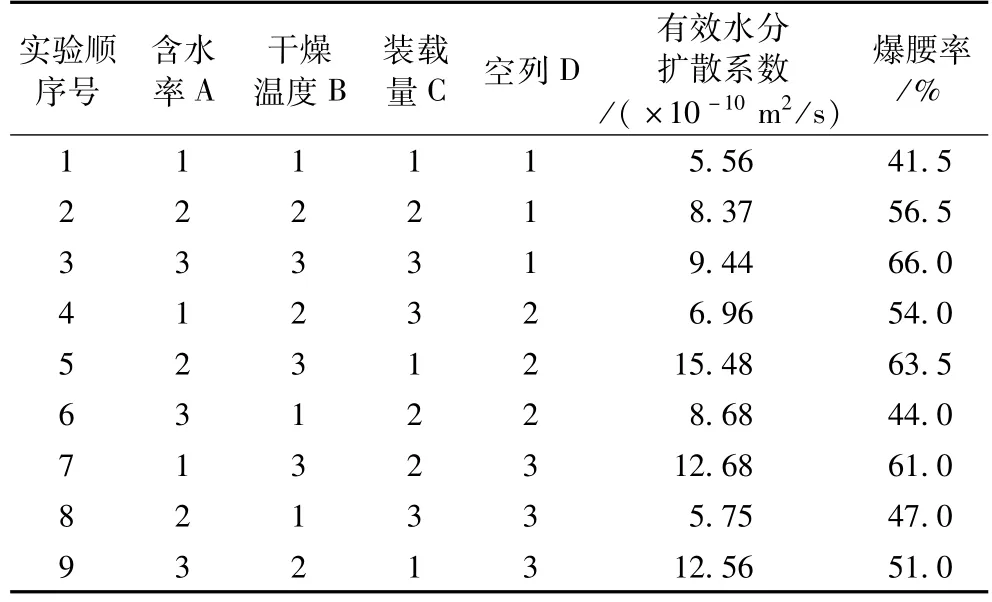
表2 样品正交实验结果分析
1.4.2 稻谷的缓苏实验
红外干燥后,将干燥后样品快速分装到27 个瓶子中,然后进行密封处理,目的是防止空气中的水分进入到样品中吸湿。将密封后的瓶子分别放置在3个小型恒温恒湿电热干燥箱中,每个干燥箱缓苏温度分别设置为45、65、85 ℃,然后每隔15 min分别从3 个干燥箱中取出1 个样品,室温冷却24 h 后,分别测出各组样品的爆腰率。
1.5 实验数据处理
每组实验将重复3 次,然后取3 次实验数据的平均值,数据分析和绘图采用Excel 软件,数据拟合分析采用SPSS19.0 软件。
2 实验结果
2.1 样品红外干燥特性的结果分析
2.1.1 含水率对样品红外干燥特性的影响
选取在装载量100 g,干燥温度60 ℃的条件下,分析水质量分数分别为24%、30%和36%对稻谷红外干燥特性的影响,结果见图1。
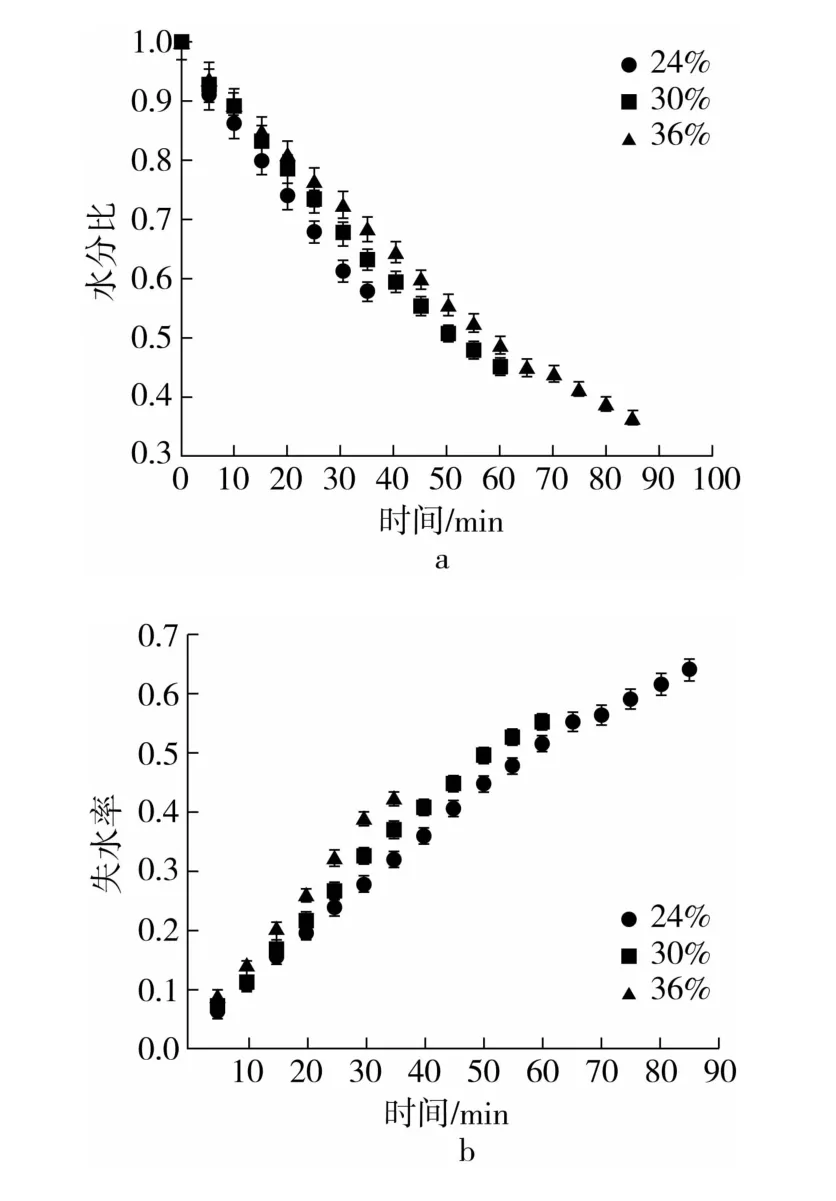
图1 样品在不同含水率时的干燥特性曲线
稻谷的水分比随着含水率的增大而变化增大,且失水率越高。稻谷在干燥前期失水率变化较大,水分比下降较快,而干燥后期,失水率变化趋于平缓。对于同一含水率条件下,随着干燥时间的延长,稻谷的失水率逐渐增加,水分比逐渐下降,且失水率随着干燥时间变化的曲线和水分比随着干燥时间变化的曲线均近似呈线性关系。当稻谷水质量分数为24%时,其失水率和水分比相比于水质量分数为30%和36%的样品,要早于达到安全含水率水平,干燥时间可以节约0.5 ~1.5 h。当样品的含水率较高时,样品内的液相水在外界温度和压力的共同影响下,使样品中心处的水分向四周传递质量变大,水分饱和度变高,促进水分比提升。相反,当含水率较低时,液相水从中心向四周传递质量变小,水分比降低。所以,样品的水分比随着样品的含水率的增大而升高。当干燥时间增加时,样品体内的液相水的含量会降低,液相水会从原来连续的状态变为非连续状态。液相水的迁移主要从孔隙内孤立的鞍状体两端弯曲液面处的热端液相水蒸发和冷端蒸汽泠凝,导致鞍状体两端构成新的弯曲页面,促使鞍状体液相水进行迁移[28]。由于受迁移影响样品液相水的传递质量要比受温度影响样品液相水传递质量要低,所以导致样品在干燥后期的水分比减小。
2.1.2 干燥温度对样品红外干燥特性的影响
选取在水质量分数为36%,装载量50 g 的条件下,分析干燥温度分别为50、60、70 ℃对稻谷红外干燥特性的影响,结果见图2。当含水率和装载量保持不变时,随着干燥温度提升,样品的水分比下降越快,而失水率不断升高。随着干燥温度不断提高,样品干燥速率越快,样品的干燥时间逐渐缩短。样品在干燥前期,其水分比和失水率随着干燥时间的增加,其变化趋势逐渐呈线性变化,并且因为样品的前期含水率较高,导致干燥时间较长。在干燥后期,样品的水分比下降趋于平缓,失水率增加幅度较小。
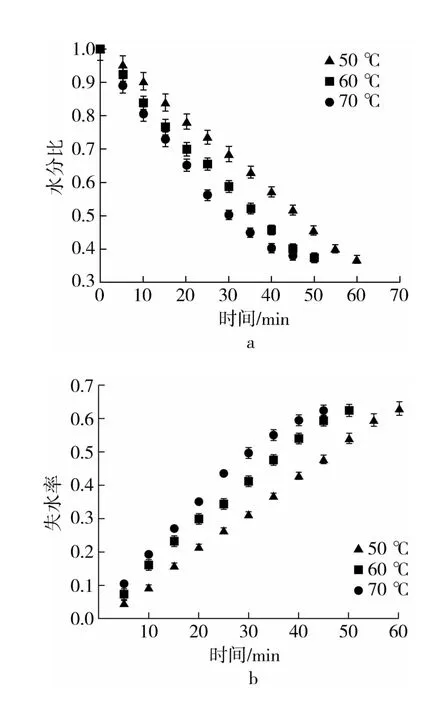
图2 样品在不同干燥温度下的干燥特性曲线
通过对实验数据结果进行比对发现,样品在干燥温度为60 ~70 ℃时,干燥速率明显更快,不过由于温度较高,其干燥后的样品爆腰率也相对较高,品质不好。样品在干燥温度为50 ~60 ℃时,干燥速率相对较慢,但干燥后样品的爆腰率较低,颗粒饱满,色泽鲜亮,品质保存较好。因此,较高的干燥温度虽然可以提高干燥速率,减少干燥时间,但干燥后样品的品质较差,而较低干燥温度对样品的影响却正好相反。所以综合考虑,样品适宜的干燥温度区间应保持在50 ~60 ℃。
2.1.3 装载量对样品红外干燥特性的影响
改进后的做法:用陆生植物叶(例如芥兰叶、非洲茉莉叶、小白菜叶、鸡蛋果叶等,只要生长旺盛、叶绿素浓角质层薄的陆生植物叶片都可以)经过横切成0.3 cm羽状代替金鱼藻;碳酸氢钠溶液浓度从0.1%提高为4.2%。这样解决了难找到金鱼藻(或其他沉水植物)的难题,拓宽了材料的来源、加快了光合作用速度。实验证明,10.0 g芥兰叶横切成0.3 cm羽状后浸入1 400 g质量分数为4.2%的碳酸氢钠溶液中在中等强光下光合作用1.5 h可以收集到28.6 mL氧气。
在干燥温度60 ℃,含水率24%条件下,分析装载量分别为50、100、150 g对稻谷红外干燥特性的影响,见图3。干燥温度和含水率保持不变时,随着装载量增加,样品水分比下降得越慢,失水率也增加得越小。同一时间段,装载量为50 g的样品进行红外干燥后,其水分比相比于100 g和150 g的样品,水分比下降最快,失水率增加最多。而装载量为150 g 的样品进行红外干燥后,其水分比下降最慢,失水率增加最少。因此,样品进行红外干燥时,最适合的装载量为50 g。
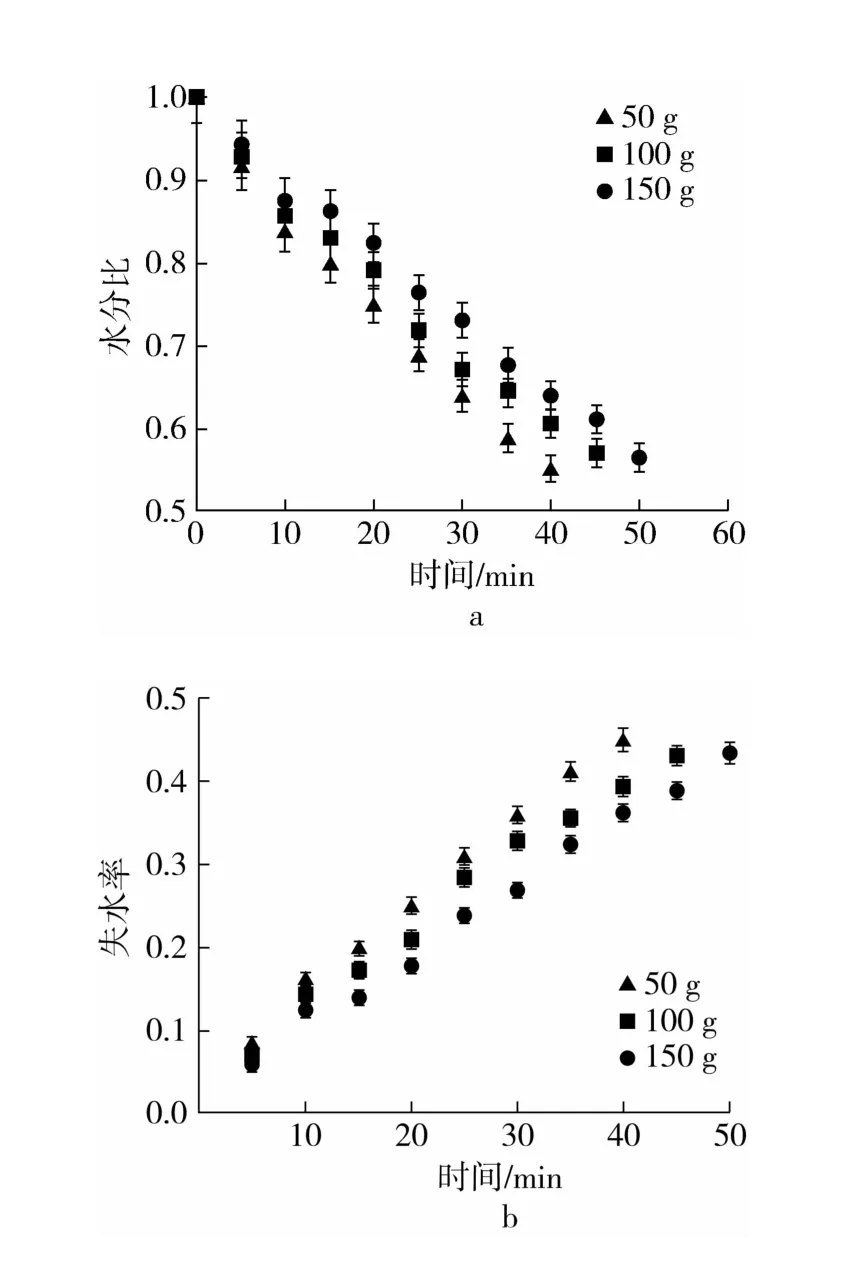
图3 样品在不同装载量下的干燥特性曲线
2.1.4 样品正交实验结果分析
根据表2 所设计的实验顺序号进行正交实验,得到样品的有效水分扩散系数结果和爆腰率。对结果进行极差分析和方差分析,其结果见表3、表4。
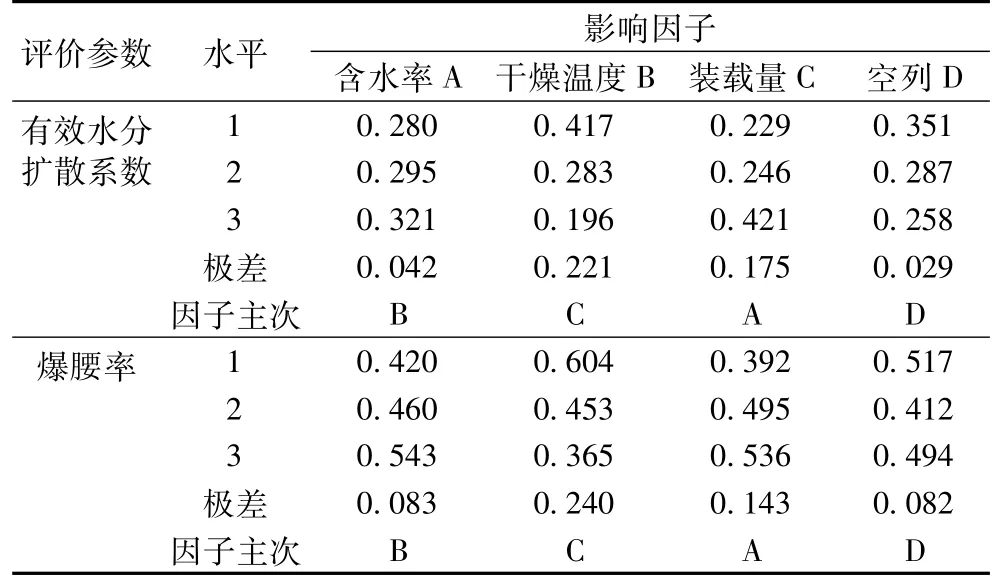
表3 极差结果分析

表4 方差结果分析
各实验号样品经过红外干燥后,其爆腰率都很高,主要原因可能是由于干燥前样品在进行吸湿预处理后使其体内含水量高,会生成一定的吸湿裂纹。样品在进行红外干燥时,由于受到了较高的温度,导致样品失水较快,体内水分梯度较大,使样品体内抗拉强度变弱,拉应力强度超过了抗拉强度,造成了样品体内裂纹的产生。干燥时间越久,样品的爆腰率增大趋势越快,造成了样品更多地爆腰。因此,为更好地降低样品的爆腰率,需要对干燥后的样品做缓苏实验处理。
对实验样品测得数据结果进行极差分析可知:3个主要因子对稻谷红外干燥工艺影响的主要排列顺序为:干燥温度B >装载量C >含水率A。从样品的有效水分扩散系数指标来看,有效水分扩散系数最大的红外干燥方案应选择A2B3C1;对于爆腰率指标而言,最小爆腰率的红外干燥方案为A1B1C1。由于爆腰率是评价样品品质好坏的一项重要指标[29],在保证干燥速率的同时,要尽可能降低样品的爆腰率,保证样品的品质影响很小或不受影响。因此,根据实验结果,结合样品有效水分扩散系数和爆腰率两个指标综合考虑,把A3B2C1作为样品最优红外干燥工艺方案,即干燥条件为水质量分数36%、干燥温度60 ℃、装载量50 g的方案。
对实验样品测得数据结果进行方差分析可知:3个主要因子对稻谷红外干燥工艺影响的主要排列顺序为:干燥温度B >装载量C >含水率A,其结果和极差分析结果保持一致。对于有效水分扩散系数指标而言,由于F0.05<FB<F0.01,F0.05<FC<F0.01,F0.25<FC<F0.10,则认为因子B 和A 对样品有效水分扩散系数的影响显著,因子C 对样品的有效水分扩散系数有一定的影响;从爆腰率的指标来看,由于FB<F0.25则认为因子B 对于样品的爆腰率有影响,而因子A和C对样品的爆腰率几乎没有影响。
因此,为降低干燥温度对于样品爆腰率的影响,保证干燥速率,且尽可能保护干燥后样品的品质,综合考虑,选取样品红外干燥最优干燥温度为60 ℃。
根据极差分析和方差分析,最终选取样品最优红外干燥方案为始水质量分数为36%、干燥温度为60 ℃、装载量50 g,通过计算得出,样品在最优红外干燥条件下的有效水分扩散系数为12.56 ×10-10m2/s,爆腰率为51%,结果能够满足实验需求。
2.2 样品的缓苏特性
根据最优红外干燥方案,将稻谷按照水质量分数为36%、干燥温度为60 ℃、装载量50 g 的条件下进行红外干燥实验,并把干燥后的样品进行缓苏实验,实验结果见图4。

图4 缓苏实验结果分析
样品在缓苏过程中,随着缓苏温度的升高,样品的爆腰率逐渐降低,当缓苏温度升高到85 ℃时,样品的爆腰率可以下降至12%左右。因为外界温度会影响样品自身温度,而自身温度又对样品的热力学特征产生重要影响。同时,稻谷是一种黏弹体,当自身温度变化时,会影响体内水分梯度,从而影响弹性形变,而稻谷的颗粒性质又会对黏性形变产生影响,从而影响样品的恢复[30]。因此,当缓苏温度升高时,可以促使样品黏性形变得以有效恢复,从而降低样品的爆腰率,保证了样品的品质。保持缓苏温度不变,当延长缓苏时间时,样品的爆腰率会逐渐降低,且缓苏时间越长,爆腰率下降的越慢。此时,样品的温度也会得到有效保持,会让样品内部分子热运动加快,有效降低样品内部水分梯度,进而不断减少样品的爆腰率。因此,提升缓苏温度、增加缓苏时间可以有效降低样品的爆腰率。当缓苏温度从45 ℃升高到85 ℃时,样品的爆腰率减少了将近7%;与未进行缓苏实验的样品相比,其爆腰率减少了将近40%,说明样品在进行红外干燥后对其进行缓苏处理,可以有效降低爆腰率,使其品质得到保证。
2.3 样品红外干燥数学模型
2.3.1 选出样品红外干燥特性最优数学模型
通过正交实验可知,影响样品红外干燥特性最显著的影响因素是干燥温度和装载量,且最优红外干燥方案为含水率36%,干燥温度60 ℃,装载量50 g。运用表5 中所列出常用的10 种数学模型对含水率为36%,装载量50 g,不同干燥温度条件下样品的实验数据进行非线性拟合,算出不同干燥数学模型的参数值,见表6。由1.3.3 评价方式来看,相关系数越大,卡方越小,均方根误差越小,证明数学模型的拟合度越好。根据表6 拟合结果可知,通过比较10种数学模型的R2、χ2和RMSE 3 个参数,得出Wang and Singh模型对实验数据的拟合度较好。模型的各参数值分别为R2=0.850 0,χ2=0.006 × 10-3,RMSE =5.568 ×10-3。将得到后的参数代入Wang and Singh模型式中,可以求出当温度为60 ℃时,Wang and Singh模型为MR =1 +0.000 066t-0.016t2。
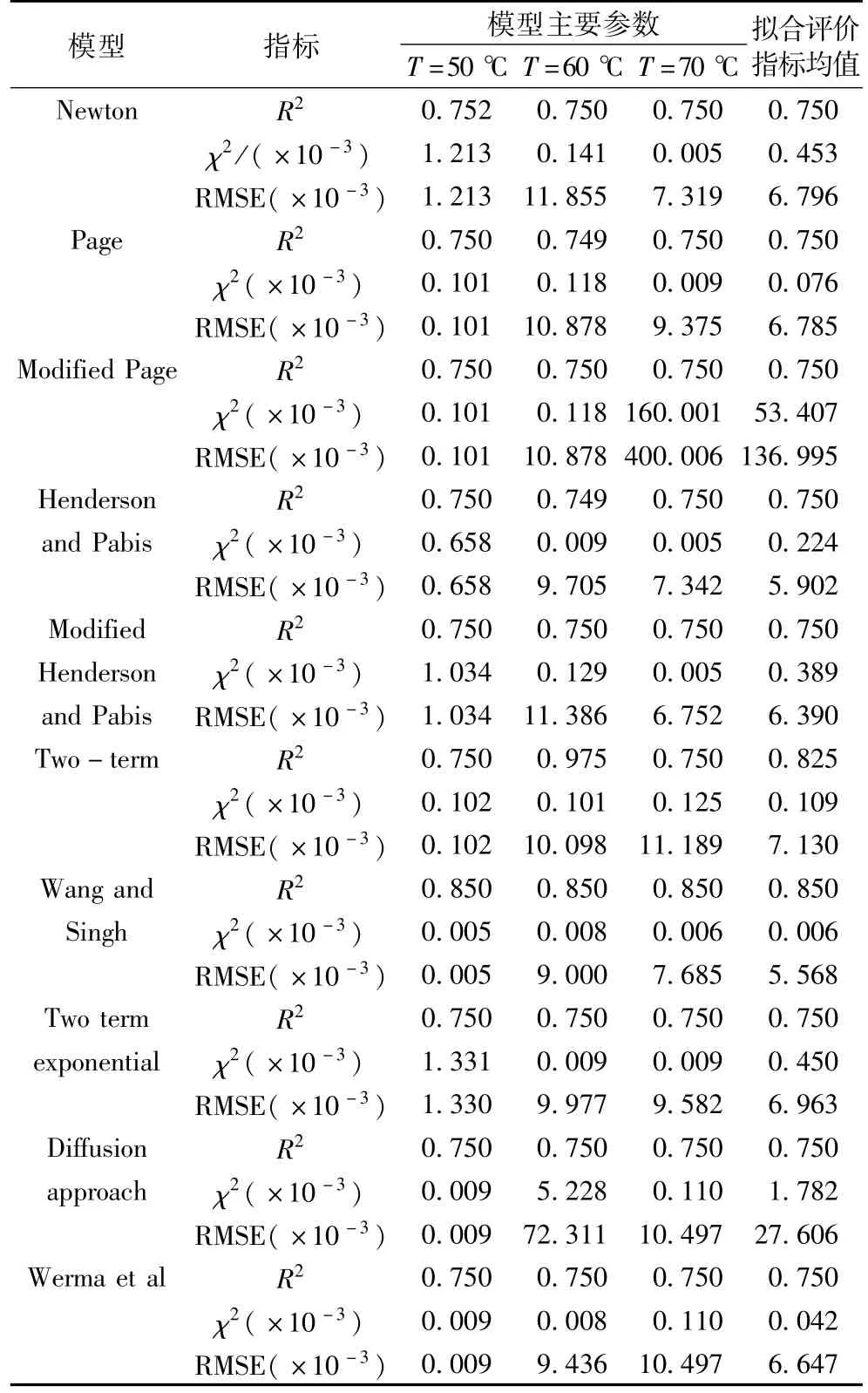
表6 样品红外干燥数学模型参数拟合结果
2.3.2 样品红外干燥数学模型的验证
对选出样品红外干燥最优数学模型进行有效验证,选取建模外的实验数据再次进行拟合分析。由正交实验结果可知,从样品的有效水分扩散系数指标来看,影响因子干燥温度和装载量对样品的红外干燥特性影响显著,影响因子含水率对样品的红外干燥特性没有影响。因此,选取干燥温度和装载量作为验证数学模型的主要影响因子,对其进行拟合,其结果见图5 和图6。从模型验证验证图中可知,无论是干燥温度作为干燥条件还是装载量作为干燥条件,所得到数据的实验值和模型值几乎相同,说明Wang and Singh模型能很好地描述样品红外干燥特性。当装载量分别为50 g和150 g时,实验值和模型值的相对平均误差分别为0.901%和1.072%;当干燥温度分别为50 ℃和70 ℃时,实验值和模型值的相对平均误差分别为0.974%和1.119%,可以得出,实验验证的数据值和模型预测的数据值具有较好的拟合度,实验验证的曲线和模型预测的曲线具有很好的一致性。

图5 装载量不同时的Wang and Singh模型验证
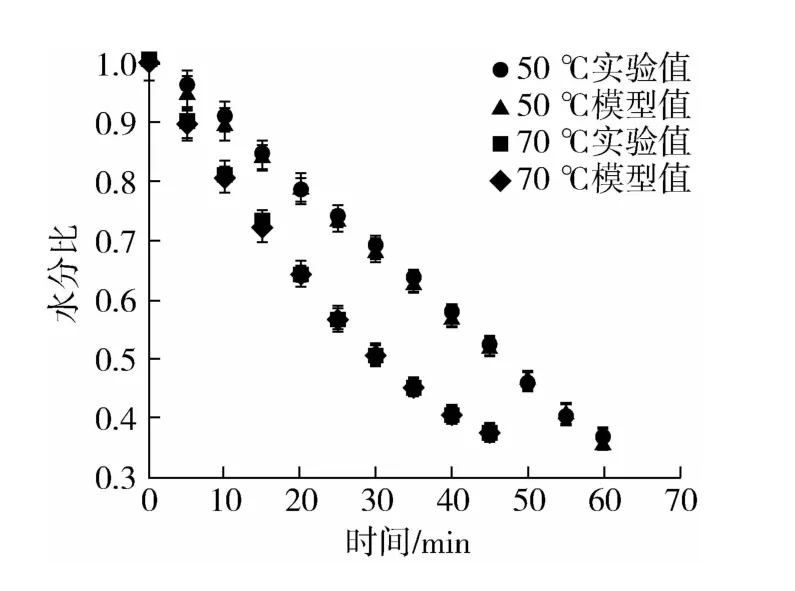
图6 温度不同时的Wang and Singh模型验证
2.4 样品红外干燥的有效水分扩散系数和活化能
根据式(4)可以把lnMR 作为因变量,把t 作为自变量,对式(4)进行线性拟合,根据直线的斜率算出样品有效水分扩散系数Deff。在水质量分数为36%,装载量为50 g的干燥条件下,干燥温度分别为50、60、70 ℃时样品的有效水分扩散系数分别为10.72 ×10-10、2.56 ×10-10、13.87 ×10-10m2/s,随着干燥温度的增加,样品的有效水分扩散系数变大。这是由于干燥温度的提升,促使样品体内液相水和蒸汽传输速度加快,让热能更有效地促进传质,从而使样品的有效水分扩散系数提高。
根据式(5),以lnDeff为因变量,1/T为自变量,绘制式(5)的曲线,并对曲线进行线性拟合,根据直线的斜率可计算出Ea。比如,水质量分数为36%,装载量50 g的条件下,样品的活化能为11.9 kJ/mol。
3 结论
稻谷在干燥前期失水率变化较大,水分比下降的较快,而干燥后期,失水率变化趋于平缓。随着干燥时间的延长,稻谷的失水率逐渐增加,水分比逐渐下降,且失水率随着干燥时间变化的曲线和水分比随着干燥时间变化的曲线近似呈线性关系。对正交实验结果进行极差和方差分析可知,3 个主要因子对稻谷红外干燥工艺影响的排列顺序为:干燥温度B >装载量C >含水率A,且稻谷最优红外干燥方案为水率为36%、干燥温度为60 ℃、装载量50 g。经过比较10 种数学模型的R2、χ2和RMSE 3 个参数,认定Wang and Singh模型为稻谷红外干燥最优数学模型,当温度为60 ℃时,Wang and Singh 模型表达式为MR =1 +0.000 066t -0.016t2。当装载量和温度分别为50 g和70 ℃时,实验值和模型值的相对平均误差分别为0.901%和1.119%,可以得出,实验验证的数据和模型预测的数据具有较好的拟合度,实验验证的曲线和模型预测的曲线具有很好的一致性。当缓苏温度从45 ℃升高到85 ℃时,样品的爆腰率减少了将近7%;与未进行缓苏实验的样品相比,其爆腰率更是减少了将近40%,说明样品在进行红外干燥后对其进行缓苏处理,可以有效降低爆腰率,使其品质得到保证。稻谷的有效水分扩散系数随着干燥温度的增大而增大,当稻谷在水质量分数为36%,装载量50 g 的干燥条件下,稻谷的活化能为11.9 kJ/mol。

