新型过载驾驶仪滚转弹制导系统稳定性研究

李 涛，付 博，王齐双，段辰璐，林时尧

(1 西安现代控制技术研究所，陕西 西安 710065；2 中国兵器科学研究院，北京 100089)

0 引言

随着世界新军事革命的深入,制导武器远程化、精确化、信息化已成为现代常规战争的趋势[1-4]。对于采用旋转体制的制导武器,由于减少了传感器数量从而简化了控制系统组成。此外,旋转削弱了激光拦截武器的打击,并可以主动借助锥形运动引起的螺线弹道进行机动突防[5]。锥形运动的诱因主要包括弹体自身的惯性陀螺效应、外形结构不对称和气动Magnus效应等动不平衡因素。

自从20世纪50年代以来,旋转弹体锥形运动的研究一直备受国内外学术界关注。早在1953年,Nicolaides就指出旋转弹体存在二圆运动特征,随着章动角的增大,弹体以螺旋前进的方式飞行,同时指明旋转弹体应避免转速闭锁导致的灾变性偏航问题[6]。Thomson指出锥形运动的回转轴为弹体的最小主惯性轴时,系统存在由能量耗散导致的锥形运动发散的趋势[7]。之后,Murphy面向无控旋转弹体,采用一阶线性化策略得出了系统动态稳定域,得出面外力矩不仅引起一个圆运动收敛,还会导致另一个圆运动的发散[8]。此外,Morote分析了旋转弹体卷弧翼带来的气动特性,指出翼面产生的马格努斯效应是导致锥形运动发散的一个重要原因[9]。针对锥形运动降低制导精度问题,现有研究表明应该使关键设计变量远离不稳定区域,而对临界状态鲜有开展更深层的研究[10-11]。

在锥形运动应对措施方面,研究表明被动削弱弹体锥形运动的成效十分有限[12]。Javier等提出在弹体前端增设一对独立的可伸缩翼片来主动抑制锥形运动[13]。Platus提出通过姿态角反馈控制方式来增加弹体固有频率,以补偿弹体滚转导致的锥形共振,使弹体远离转速闭锁区域[14]。采用主动抑制法的关键问题在于执行机构能否及时准确地响应指令,否则可能加剧锥形运动。此外,弹体自旋会引起偏航与俯仰通道之间严重的交叉耦合作用,因而采用传统分通道设计自动驾驶仪难以确保弹体锥形运动稳定性。针对此问题,Yan等建立了考虑惯性耦合、气动耦合以及控制耦合的滚转弹体姿态运动模型,同时按照非旋转弹体控制回路拓扑思路设计出旋转弹体姿态驾驶仪和阻尼控制回路,并且推导出控制系统稳定性条件[15-16]。Li等基于旋转弹的经典三回路驾驶仪的回路拓扑结构,推导出系统的稳定性设计准则[17-18]。Zheng等研究了雷达制导滚转导弹锥形运动的动态稳定性,提出了一种考虑天线罩寄生回路的复合数学模型,推导了滚转导弹锥形运动动态稳定性的充要条件[19]。Tian等基于复变形式的微分方程,获得了考虑寄生效应的伪攻角反馈三回路自动驾驶仪滚转弹稳定性的充要条件[20]。

现有考虑隔离度寄生回路的滚转弹锥形运动稳定性的研究中,主要引入经典三回路/伪攻角反馈三回路等常见过载驾驶仪,分析雷达导引头天线罩误差/捷联导引头惯性器件标度因数偏差导致的导引头隔离度问题。但基于增稳回路直接采取加速度反馈的新型三回路过载驾驶仪,开展滚转弹锥形运动动态稳定性的研究较少。文中针对上述问题,基于平台图像导引头干扰力矩引起的隔离度寄生回路,分析推导了考虑寄生效应的加速度反馈增稳新型驾驶仪滚转弹体稳定性条件,进一步分析隔离度、总延迟角和加速度计安装位置等滚转弹重要参数对包含隔离度寄生回路的滚转弹体动态稳定域的影响,为包含隔离度寄生回路的多种回路拓扑结构过载驾驶仪制导系统的动态稳定性研究提供理论参考。

1 数学建模

1.1 滚转弹动力学模型

为研究存在隔离度寄生回路情况下的滚转弹体动态稳定性问题,依据文献[16-18],引入非滚转框架下滚转导弹的六自由度动力学方程:

(1)

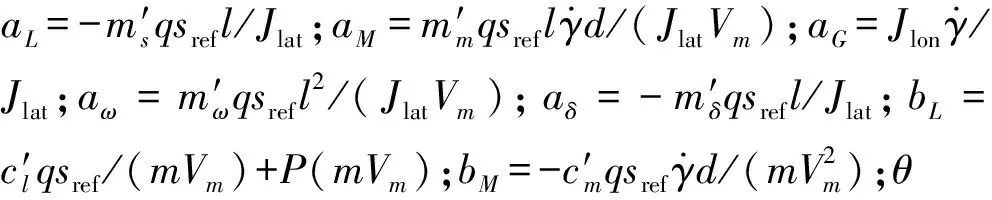
通过定义复角度αc=β+jα和δ=δv+jδz,可以得到滚转导弹的线性化复微分方程:

(2)

1.2 新型驾驶仪滚转弹制导系统模型

在经典三回路过载驾驶仪结构中,中间增稳回路的信号采取角速率的积分。在文献[21]提出的新型三回路驾驶仪结构中,增稳回路直接采用加速度计的测量信号,其结构如图2所示,下面基于该新型过载驾驶仪开展滚转弹制导系统稳定性研究。

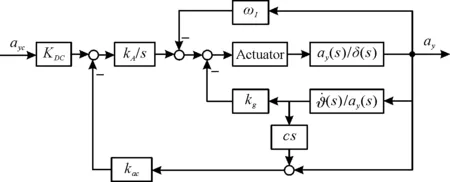
图2 新型过载驾驶仪Fig.2 New overload autopilot

基于滚转弹制导原理,引入图2所示的新型驾驶仪模型与隔离度Rd,建立图3所示的考虑隔离度寄生回路的新型驾驶仪滚转弹制导系统模型。

图3 包含隔离度寄生回路的新型驾驶仪滚转弹制导模型Fig.3 Guidance model of the new autopilot considering disturbance rejection rate

2 新型驾驶仪滚转弹制导系统动态稳定条件推导

因为存在隔离度寄生回路,滚转弹的动态稳定性不仅取决于新型驾驶仪,还会受隔离度Rd、导航比N以及弹目相对接近速度Vc的影响。考虑隔离度寄生回路的新型驾驶仪制导指令可表示为:

(3)

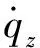
(4)

通过定义复角δc=δyc+jδzc和φ=ψV+jθ,则舵机的指令可表示为:

(5)

滚转弹的俯仰与偏航通道的舵机动力学采取二阶动力学模型,舵机输出与输入间的关系表示为:

δ=kskr(-δzcsinγd+δyccosγd)+
jkskr(δzccosγd+δycsinγd)=
kskr(cosγd+jsinγd)δc

(6)

基于获得的复数模型,可使用复系数系统稳定性判据来推导滚转导弹的动态稳定性条件。将式(5)代入到式(6)中,可得:

(7)

将式(7)代入式(2)可得:

(8)

(9)

制导系统对应的特征方程为:

(10)

根据附录A,PN/新型驾驶仪滚转弹体制导系统稳定的充分必要条件为:

(11)

3 动态稳定条件仿真验证

3.1 隔离度寄生回路对动态稳定条件的影响

为验证所推导的稳定条件,滚转弹的参数如表1所示。在仿真中的其他参数设置为:ω=8π rad/s,N=4,kac=0.0017,C=0,α0=4°。

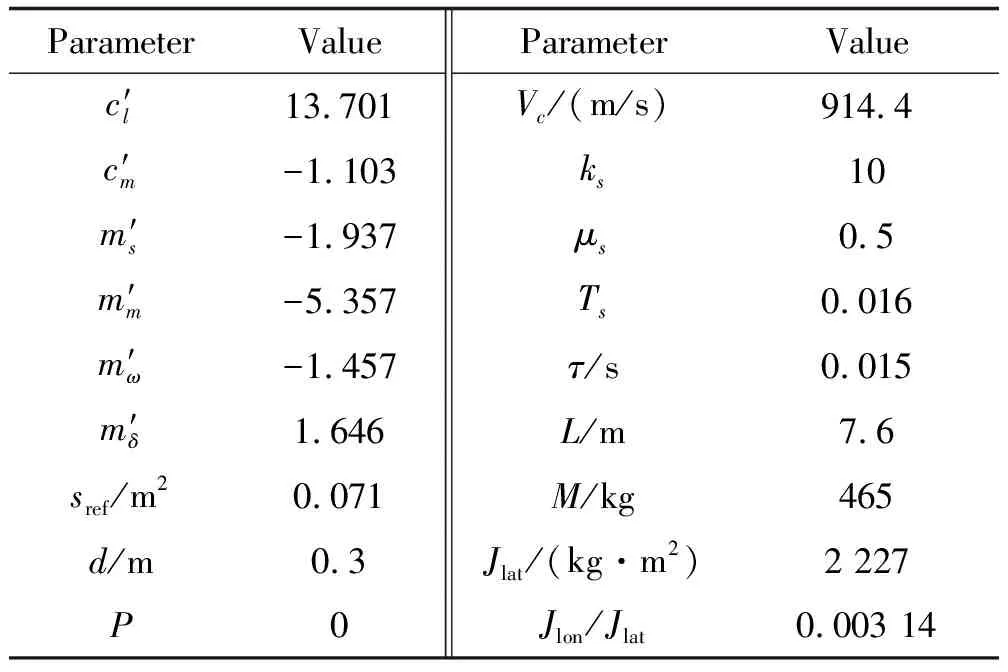
表1 滚转弹参数设置Table 1 Parameter setting of rolling missile

3.1.1 不考虑隔离度寄生回路

不考虑隔离度寄生回路,此时驾驶仪决定了PN/新型驾驶仪滚转弹体制导系统的稳定性。按照设计新型驾驶仪的稳定条件,设计参数选取为:kA=0.0088,kg=0.14,ωI=0.0315。则初始扰动α0=4°作用下,不考虑隔离度寄生回路的PN/新型驾驶仪滚转弹体制导系统仿真结果如图4所示。

图4 不考虑隔离度寄生回路的滚转弹稳定状态Fig.4 Stable state of rolling missile disregarding disturbance rejection rate

若不考虑隔离度寄生回路,在初始扰动影响下系统状态逐渐收敛至零,说明新型驾驶仪设计参数可消除由初始攻角误差引起的锥形运动,从而保证滚转弹的动态稳定。此外,由于俯仰与偏航通道存在交联耦合,纵向平面内的初始攻角误差会引起侧向平面的运动。

3.1.2 考虑隔离度寄生回路

当考虑隔离度寄生回路时,PN/新型驾驶仪滚转弹体制导系统的稳定性取决于制导系统参数。选用满足新型驾驶仪稳定的设计参数,即kA=0.0088,kg=0.14,ωI=0.0315。分别选取了NVcRd=50,NVcRd=367两种情况进行仿真验证,结果如图5～图6所示。

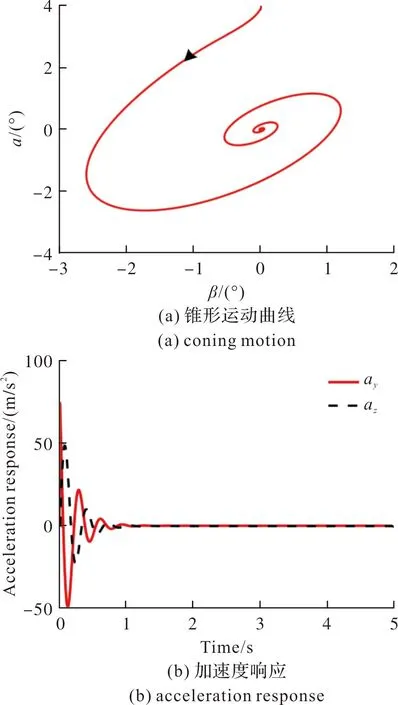
图5 NVcRd=50时滚转弹稳定状态Fig.5 Stable state of rolling missile considering NVcRd=50

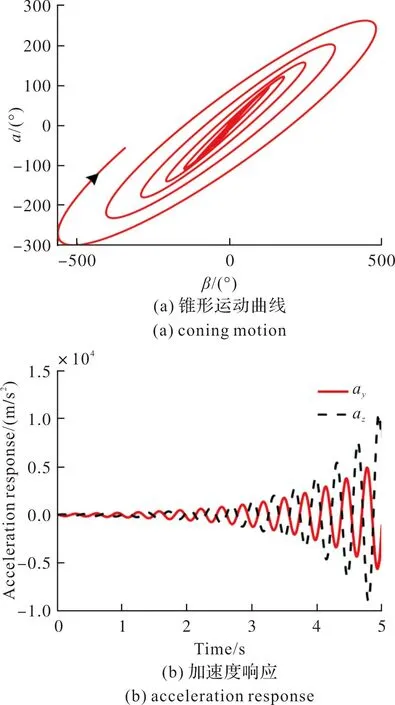
图6 NVcRd=367时滚转弹失稳状态Fig.6 Instable state of rolling missile considering NVcRd=367

隔离度在一定程度上延缓了制导系统的响应速度。当NVcRd=50时,隔离度组合参数满足稳定性的限制条件,在初始扰动α0=4°影响下,制导系统快速收敛至零;当NVcRd=367时,隔离度组合参数超出稳定性限制边界,初始扰动影响下制导系统发散。

3.2 制导系统参数对动态稳定条件的影响

新型过载驾驶仪制导系统的稳定性会受隔离度寄生回路组合参数的影响,合理选取新型过载驾驶仪设计参数及其他制导系统参数,可减弱隔离度的不良影响,从而抑制制导系统发散、提升制导系统响应速度。

3.2.1 不同驾驶仪参数对动态稳定条件的影响

选取滚转弹转速为ω=8π rad/s,导航系数N=4,驾驶仪加速度反馈增益kac=0.0017,弹体参数见表1。求得不同驾驶仪设计参数稳定域如图7所示。

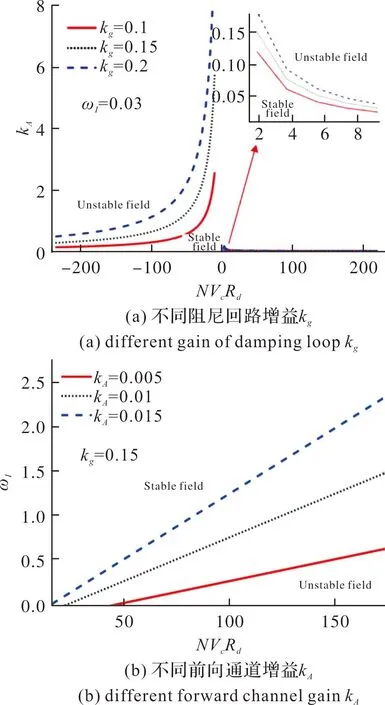
图7 新型驾驶仪参数稳定域Fig.7 New autopilot parameter stability region

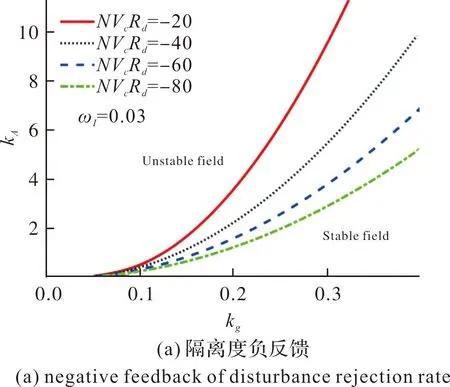
图8 隔离度对新型驾驶仪参数稳定域的影响Fig.8 The influence of disturbance rejection rate on the new autopilot parameter stability region

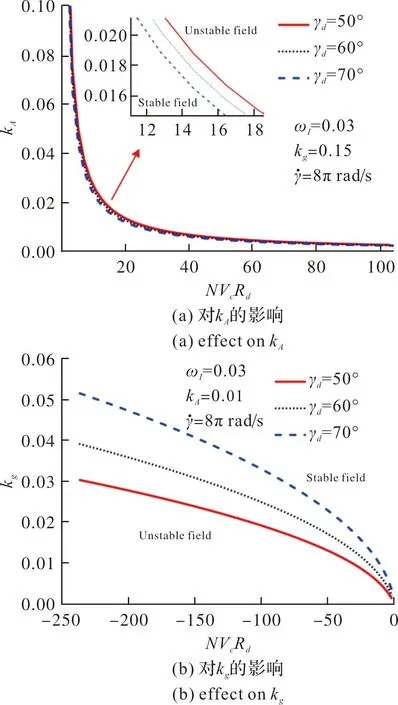
图9 总延迟角对参数稳定域的影响Fig.9 Influence of total delay angle on parameter stability region

增大前向通道增益kA,将会减小系统参数稳定域;增大阻尼回路增益kg,将会增加系统参数稳定域。此外,随着隔离度组合参数NVcRd绝对值的增大,系统参数稳定域减小。

3.2.2 不同隔离度对动态稳定条件的影响

对于包含隔离度寄生回路的PN/新型驾驶仪制导系统,隔离度无论是负反馈还是正反馈,都将减小系统参数的稳定域;同时,随着隔离度绝对值的增加,设计的前向通道增益kA越小。

3.2.3 不同总延迟角对动态稳定条件的影响

总延迟角对新型驾驶仪前向通道增益kA的影响很小,甚至可以忽略;总延迟角越大,设计的阻尼回路增益越大,从而保证弹体有足够的阻尼维持稳定。

3.2.4 不同加速度计位置对动态稳定条件的影响

选取滚转弹转速为ω=8π rad/s,导航系数N=4,设计临界稳定参数为:加速度计位置C=0,加速度反馈回路增益kac=0.0017,增稳回路增益ωI=0.0315,阻尼回路增益kg=0.14,前向通路增益kA=0.0088,隔离度组合参数NVcRd=209。基于以上设计参数进行仿真,结果如图10所示。

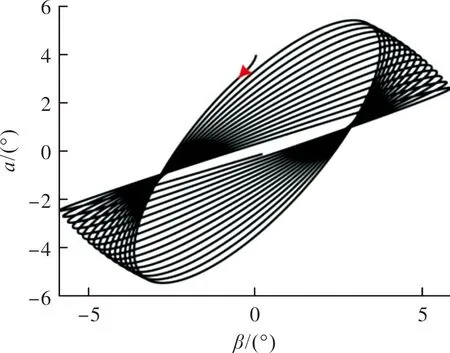
图10 C=0时临界稳定的锥形运动Fig.10 Coning motion maintain critical stable when C=0

设计的PN/新型驾驶仪系统参数使系统处于临界稳定的状态。使用相同的设计参数,改变加速度计的位置,仿真结果如图11所示。

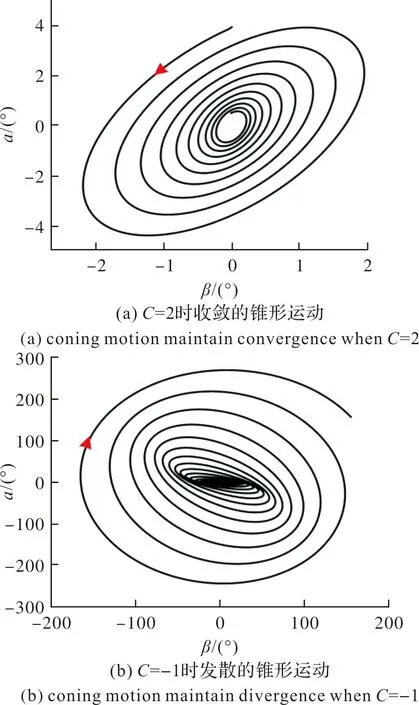
图11 加速度计位置对稳定性的影响Fig.11 Influence of accelerometer position on stability

当C=2时,即加速度计安装在弹体质心之前,可使临界稳定系统趋于稳定;当C=-1时,即加速度计安装在弹体质心之后,可使临界稳定系统发散。因此,加速度计安装在弹体质心之前有利于PN/新型驾驶仪制导系统的稳定。

4 结论

针对制导弹箭锥形运动不稳定导致制导精度变差的问题,基于图像导引头干扰力矩引起的隔离度寄生回路问题,开展了滚转弹动态稳定性研究。分析推导了考虑寄生效应的加速度反馈增稳新型驾驶仪滚转弹体稳定性条件;系统参数稳定域与隔离度幅值、驾驶仪前向通道增益和舵机总延迟角成反比,与驾驶仪阻尼回路增益成正比。此外,总延迟角主要影响驾驶仪阻尼回路增益的设计,加速度计安装于质心之前有利于滚转弹体制导系统的稳定。因此,滚转效应、寄生效应与控制指令延迟是导致驾驶仪参数设计稳定域减小的主要因素,驾驶仪设计参数应远离稳定性边界从而提升锥形运动稳定性。