基于旁孔透射法的隧道锚杆长度检测方法
徐方林,周运刚,姜 伟
(1.青岛地铁集团有限公司,山东 青岛 266100; 2.上海同是科技股份有限公司,上海 201203)
隧道锚杆作为主要受力部件,其锚固长度在隧道围岩支护过程中是非常重要的指标。但由于其为隐蔽工程,锚杆长度的检测一直受到检测环境的限制。旁孔透射法于20世纪90年代初被欧美国家运用于实际工程当中,S.T.Liao等[1]根据Snell定律把深度时间曲线首至波连线拟合成两条线段,提出将交点处确定为桩身长度。近年来旁孔透射法检测基桩不断发展,国内相关学者分别研究了旁孔透射法的理论,建立简化计算模型,并提出各种修正方法[2-5]。目前旁孔透射法在建筑基桩检测中技术已趋于成熟,且相关规范已建立完善[6]。
传统的锚杆检测检验方法主要采用位移收敛计、顶板离层指示仪、拉拔计等设备,但是会对锚杆锚固带来不可逆的损伤和破坏,乃至危害整个锚固工程的质量[7]。随着无损检测技术的发展,相应技术逐渐应用到锚杆检测之中。常用的检测方法包括应力波法、超声波法等[8-9]。但是由于锚杆锚固系统工况较为复杂,波在传播过程中波形不明显,同时噪声等不良因素的存在,也对检测造成不可避免的误差。因此,本文借鉴旁孔透射法的原理,将其应用于隧道锚杆长度检测之中,并利用数值模拟软件ABAQUS进行仿真分析,验证其可行性。
1 旁孔透射法原理
1.1 基本原理
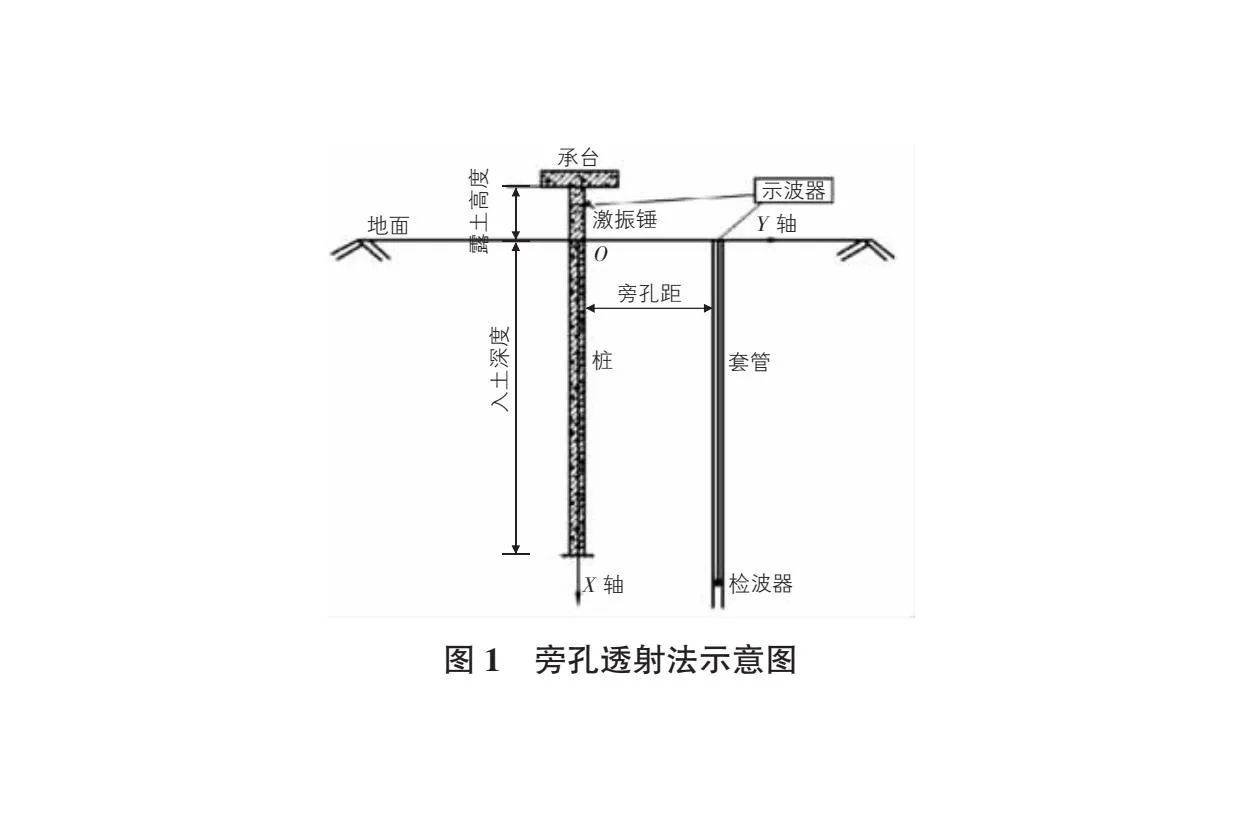
旁孔透射法最早是一种用于确定基桩长度,进行基础完整性检测的方法[10]。如图1所示,旁孔透射法的仪器包括激振源、捡波器和信号采集装置。检测前,在桩身附近预埋平行套管,套管内注满清水。检测时,将捡波器放入套管内,在基桩外露部分用激振锤敲击,同时用套管内的捡波器采集不同深度透射波信号,然后通过信号采集装置对信号进行分析处理即可判断基桩的长度和完整性。
旁孔透射法应用于基桩检测是基于一维弹性波理论的。根据费马原理,波总是沿着历时最短的路径进行传播。该原理为首至波传播路径与历时提供了数学基础。由Snell定律,激振后波沿桩中传播会产生折射纵波(PP)和折射横波(PS)。由于桩身中弹性波速大于周边土体波速,因此旁孔内检波器最先接收桩身内弹性波。
如图1所示,当基础侧面或承台顶产生压缩波(P波)或剪切波(S波),所得应力波沿桩身向下传递,利用旁孔中检波器收集土中由桩身透射所传递的信号,由首至波信号时间深度关系拟合得出时间深度曲线,由检测所得波速即可确定桩身长度。当激振产生应力波沿桩身传播距离大于2倍桩身直径且桩土间存在较大波阻抗差异时,平面波传播性质与一维波相似。因此,在介质变化分界面,波阻抗发生改变,根据折射理论,沿深度对速度-时间曲线进行拟合,根据拟合的直线即可判断桩底或者缺陷位置。拟合成的两条直线的斜率即代表桩身的波速和桩底土的波速。
1.2 桩身长度确定方法
目前,桩身的确定方法大多采用两直线交点法。旁孔透射法简化计算模型如图2所示[11]。当桩身在S处进行激振,产生的弹性波沿S-O-A-R路径传播,其历时经过简化后即可表示为:
(1)
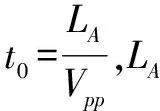
(2)
其中,Vps为地基土三维P波波速;θ为桩土间透射角。
由式(1)可知t-Z关系为一条直线,即图3中l1。该直线关于时间轴的斜率即桩中一维P波波速Vpp。
在均质地基中,当桩身下行波到达底端B点按角度θ传播到达C点以下任意位置F,当满足Z-L≥5D时,相应的历时即简化为:
(3)
因此,此时时间-深度关系已趋于一条直线,即图2中的l2,其斜率即为地基土中的波速。
当旁孔距较小时,两条直线交点处的纵坐标即可近似视为桩底的深度。

2 隧道锚杆长度无损检测方法
上述旁孔透射法应用于基桩深度检测时所涉及的理论已有研究表明同样适用于隧道围岩中[12]。因此基于上述理论,提出隧道锚杆长度的无损检测方法,如图4所示。

该装置包括激振波接收处理器、用于敲击锚杆顶端的激振锤、置于锚杆外露段的首波接收器、探测杆以及等间距布置在探测杆上的若干水听器。使用时,若干个水听器串联后与激振波接收处理器电连接,在锚杆周围的围岩上开设深度大于锚杆设计长度的测洞,将探测杆和水听器均置于测洞里。使用激振锤敲击锚杆外露端,水听器能够分别接收激振锤敲击锚杆顶端产生的激振波并传送给激振波接收处理器。使用磁铁将首波接收器固定在锚杆外露端,首波接收器为应力波传感器,能够接收激振锤敲击锚杆顶端产生的激振波并传送给激振波接收处理器。最后通过激振波接收处理器计算水听器传送的激振波分别与接收到的首波接收器传送的激振波的时间差。由此即可计算锚杆的长度。
3 基于ABAQUS隧道锚杆长度检测仿真分析
锚杆模型长度为4 m,直径取4 cm,长度为6 m,直径为40 cm。根据一维弹性波理论,锚杆和围岩中的波速由式(4)计算:
(4)
锚杆和围岩的材料参数参考《公路隧道设计规范》进行定义,材料参数如表1所示。

表1 材料参数设置
围岩材料模型选择摩尔-库仑模型,内摩擦角为55°,黏聚力为2.0 MPa。锚杆选择动态面面接触(STS),接触算法为对称罚函数法[13],即在每一个分析步中,首先检查节点是否穿透主界面,没有的话则不作处理,若存在穿透的话,则在主界面和节点之间施加数值较大的接触力(力的大小由主面的刚度和穿透深度决定),转换成物理关系,即在主从界面之间加入一个刚度较大的弹簧,来减轻从面节点为主面的穿透程度。边界条件的设置包括:锚固底端、锚固体周围。对于锚固底端,因为其不会发生任意方向的位移,设置为“完全固定”;对于锚固体周围,约束X,Y方向上的位移并设置为0。对实体进行网格划分,以扫掠的形式划分成六面体网格。
激振方式采用均布激振力,利用激振锤产生均布瞬态激振,激振力脉冲为半正弦脉冲[14],大小为:P=P0sinωt,0 对上述模型提交后其结果如图6所示,结果文件显示应力确以波动的形式向锚杆底端传播,经过锚杆底端的围岩反射后发生折返。波动的产生表明所建立的有限元模型是合理的。提取距离锚杆边缘20 cm处一条直线上的速度随时间的变化,距离锚杆顶端0.5 m处的速度-时间曲线如图6所示。 每隔0.5 m分别布置一个测点,提取各个测点时间-速度数据,绘制各个深度的波形图如图7所示。利用Matlab自动识别提取峰值点,并进行线性拟合,拟合结果如图8所示。图8中两条直线相较于4.06 m深度处,误差为1.5%。4 m以上的直线其斜率为5 090.18,相较于计算所得波速误差为1.19%;4 m以下直线斜率为3 576.4,误差为2.3%。分析误差产生的原因,主要包括两个方面:其一,在围岩中把时间-深度曲线看作为一条直线的条件是Z-L≥5D,但是当0 隧道工程建设过程中,锚杆锚固长度的检测受到施工环境的限制,不能得到准确的检测数据,本文借助于旁孔投射法原理,利用激振波接收处理器、激振锤、首波接收器、水听器装置组成锚杆检测仪器,通过波传导时间差来计算锚杆的长度,有效的解决了施工环境带来的检测难题,同时利用数值模拟软件建立有限元模型,通过数值模拟计算与室内试验得到的结论基本相同,从而证明使用旁孔透射法检测隧道锚杆长度在理论上是可行的,本次研究为隧道工程建设过程中的锚杆锚固长度检测提供了参考价值。



4 结语

