基于AHP的风电机组变桨系统权重分析

邹继行 张金双 刘晨光

（华北理工大学）

0 引言

常规能源在世界的发展中有着不可磨灭的贡献，随着常规能源劣势的显现，新能源异军突起，其中风能以其清洁和可再生的优势迅速崛起。风力发电在世界范围内发展迅速，很多地区都建设了大量的并网风力发电机组［1-4］。在风电场中风电机组是一个结构复杂，各设备之间关联关系密切的一个系统。在风机出现故障时应该对故障进行及时有效的预测、解决，从而减少风机停机时间进而实现风电场效益最大化［5-6］。

在风电机组远程监控系统中，当系统中设备参数超过设置的阈值时，很难确定是风电机组具体哪一设备发生了故障。这给风电场工作人员带来了极大的不便，工作人员需要对整个风电机组进行诊断，这样就浪费了大量时间，使得风电场经济效益降低。针对这一系列问题，行业内专家进行了广泛的研究和分析，力求在风机故障时能最大效率的解决问题，保证风机安全运转［7］。

在现代风电机组系统中的变桨系统一般采用液压变桨结构形式，能够在正常工况下进行工作。针对此情况本文针对风电机组容易出现故障的变桨系统进行分析，对影响风电机组变桨系统的因素进行权重分析，从而实现根据风电机组SCADA系统的实时数据综合判断是否是风电机组变桨系统出现了故障［8-9］。

1 基于SCADA系统数据的故障诊断

1.1 风机故障模式及其原因

SCADA系统即数据采集与监视控制系统，它可以全天候的对风机进行数据采集和遥测控制。对于风机的故障诊断技术，其基础就在于监控系统内的遥测、遥调等信息，通过结合其他外在因素，对风机实时运行情况进行准确的判断。如果风机突然出现异常情况，可以运用以上技术进行快速处理，最大程度的减小风机检修时间。在工程实际中，风机可能会出现多种异常情况和突发故障，表1中为保定某风电场监控系统内常见的几种故障和原因。

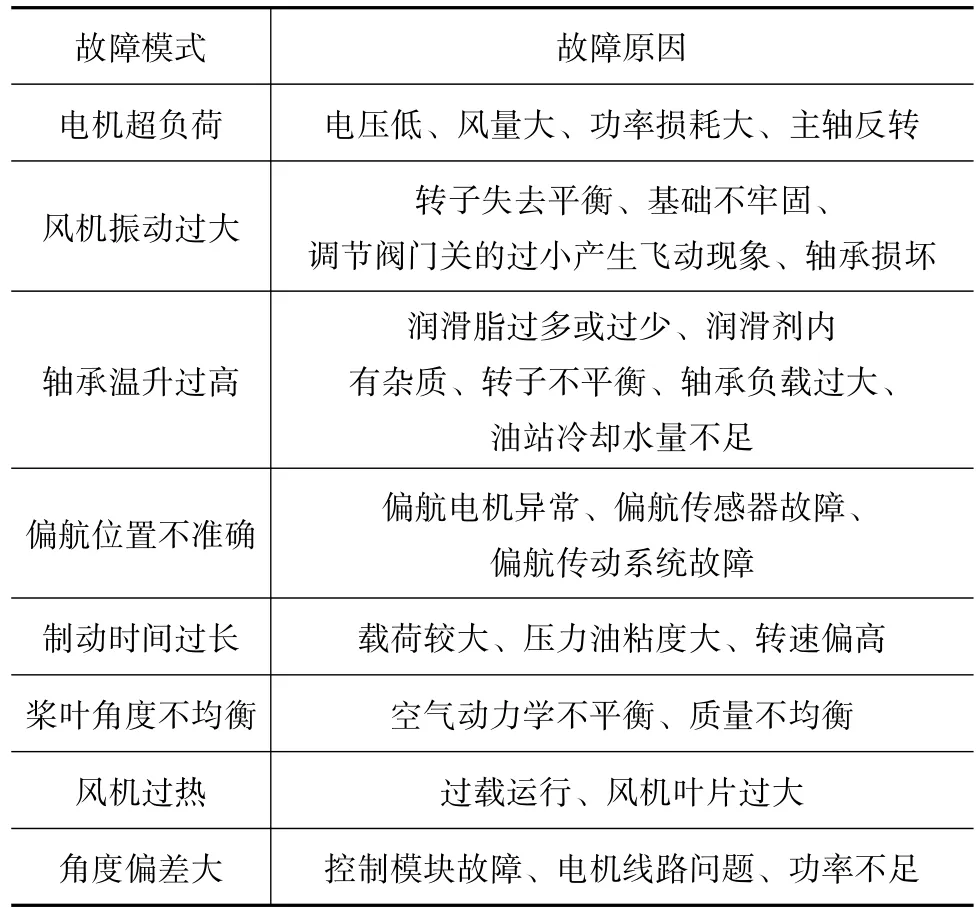
表1 风电场监控系统内常见的故障和原因

1.2 风电机组阈值设计

在风力发电机的SCADA系统中，有一个完善的报警机制。一旦风电场中的风电机组出现任何故障，相关的运行数据就会立刻超过预设的安全范围。这时，监控系统会立即触发报警，同时显示出异常情况，以便工作人员进行及时处理。对于在恶劣情况下，风电机组设备的阈值设置尤为重要，但是在有些条件下需要综合考虑各方面的因素，才能完成对风电机组中某个设备准确诊断。

2 变桨系统故障分析

风力发电机组的结构复杂且各个部分相互关联，因此当某个检测量超出阈值时，确定具体故障位置具有一定的挑战性。为了解决这一问题，进行综合判断就显得尤为重要。

风力发电机中的变桨系统受到多种参数的影响。随着风速的变化，风电机组中发电机的旋转速度也会有所改变，再者，风机运转中的有功和无功输出也会干扰其变桨系统的参量。由此我们可以判断出，只有对风机变桨系统内部结构的重要元件实现实时采集和控制，才能对其进行精确的故障诊断。这些元件包含驱动电流、散热装置和其他关键元件。通过实时收集和分析这些数据，我们可以更好地了解变桨系统的运行状况，从而进行准确的故障诊断和维护。表2列举出了监控系统及变桨系统中相关的部分参数。

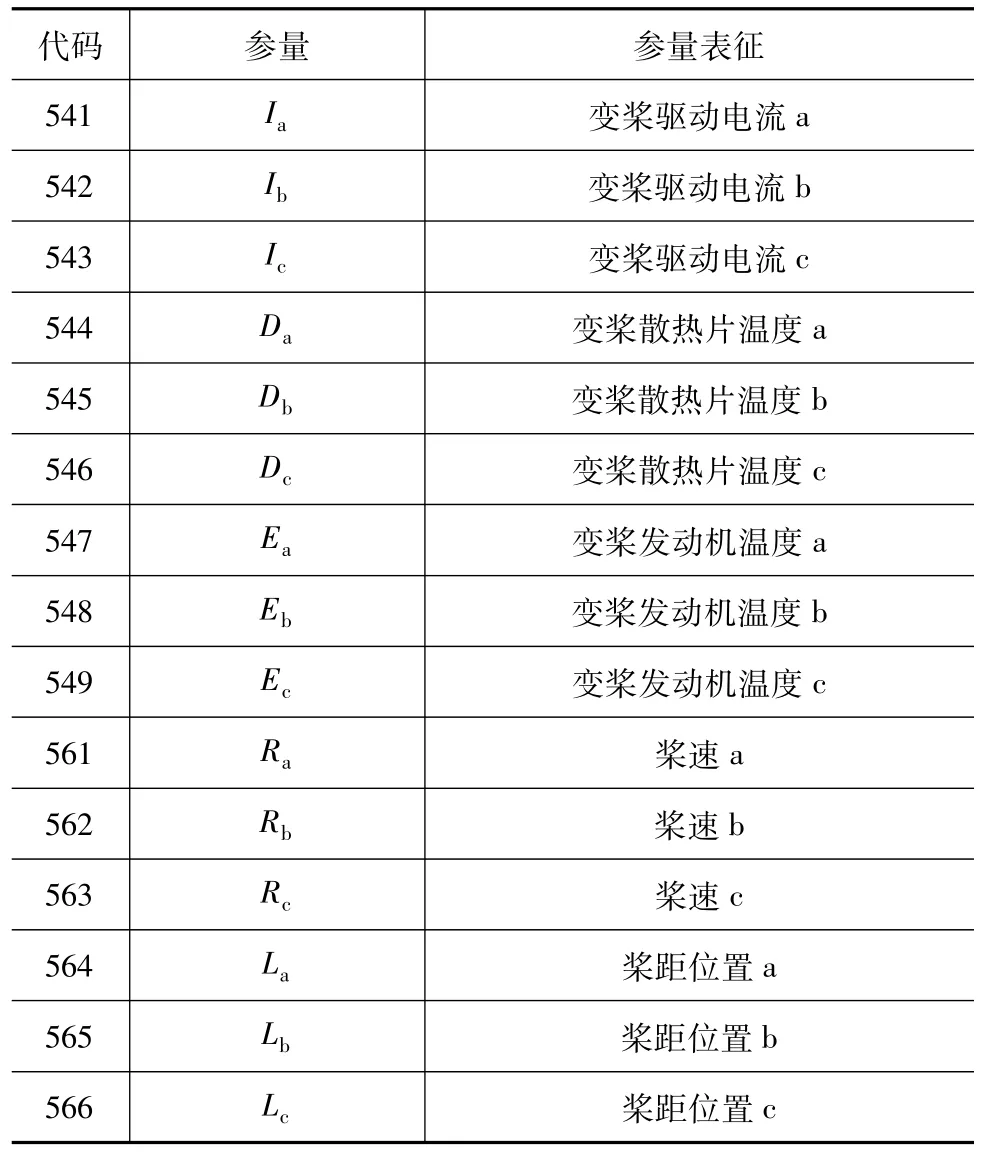
表2 监控、变桨系统有关参数

3 风机变桨系统权重分析

3.1 变桨系统扇叶归类分析

结合工程实际，为了提高故障诊断系统的精确程度，本文引入有关风机变桨的某些元件的权重因素，通过分析，能够简洁快速的判断风机变桨的实时情况。通过a号、b号、c号扇叶的变量进行权重计算时，考虑到它们的对称性和一致性，我们可以将它们归为同一类别。具体来说，我们把a～c号3个扇叶桨距角当做一个扇叶桨距角；把a～c号3个扇叶驱动电流当做一个扇叶驱动电流；把a～c号3个发动机温度当做一个变桨发动机温度。通过这种方式，我们可以更有效地进行权重计算和分析。

3.2 层次分析法在变桨系统中应用

对风机系统进行权重分析时可采用多种方法，本文主要选取层次分析法（AHP）。层次分析法的应用形式主要通过以下几点来进行：

（1）构建层次架构

通过分析风机系统，需要针对实际工程问题需要来构建一个分层的模型。通常这个模型结构包含三个级别。最顶层是目标层，一般来说，在这一层中我们只关注一个关键因素。接下来的一层是准则层，这一层的数量可以根据实际需要来确定，可能包含多个层级，或者只有一层。最底层是方案层，方案层比较容易确认。

（2）建立判定矩阵

通过数值计算和分析判别，构造出一个判断矩阵A。矩阵A的表示方式如公式（1）所示：

公式（1）里aij的下角标注既体现了在矩阵A中的坐标，还体现了变量x和y之间的重要性比值［10-11］。通过AHP分析，通过对逐样元素开展两两比较来赋予其相应的权重。通过衡量某个属性的相对权重，整合出1～9标度法，对比不同的元素来推导标度值，其解释和意义见表3。矩阵A中，互为倒数的斜线两旁互为对角的变量值，为1的是斜线上的变量值。

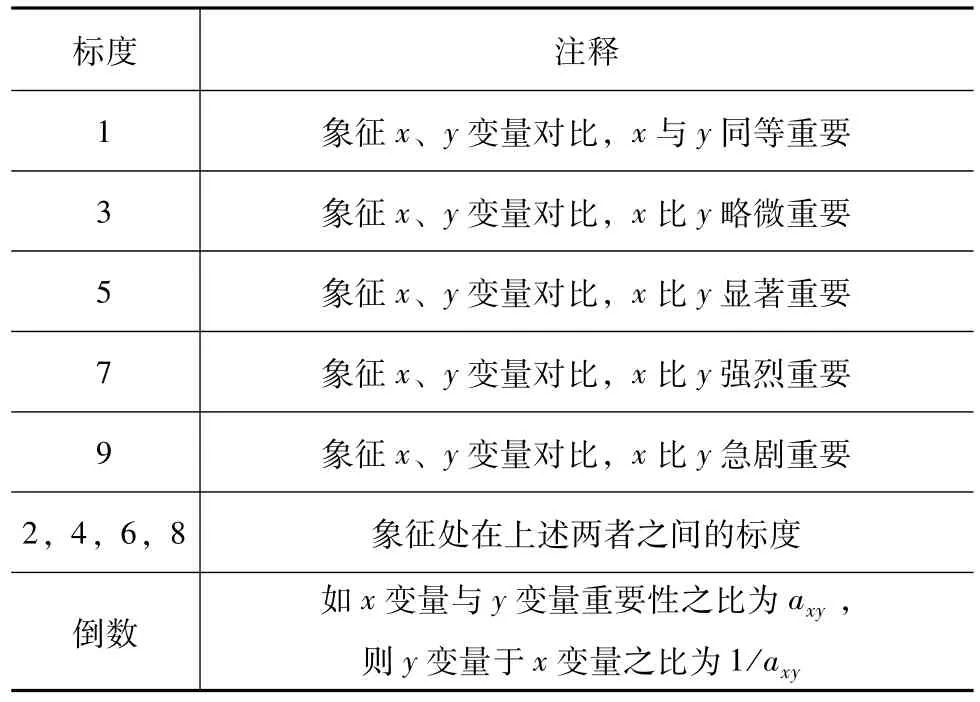
表3 比例标度量化表

（3）特征值同一性判断

进行判断矩阵计算时，最大特征根对应的特征向量为权重值，对该特征向量进行归一化处理的结果即为该层中各个元素相对于上一层因素的重要性排序［12］。为确保此理论所得结果的可靠性，应对整体架构与判别矩阵开展同一性判断［13］。同一性的偏差通过公式（2）进行计算，其中CI被称作同一性变量。

式中，λmax被称作极大特征向量。

在对同一性偏差进行判别的过程中，为了考虑差异维数的矩阵可能对应的同一性变量，我们使用平均任意同一性变量RI。而同一性比值CR反映了不同维数矩阵的同一性水平，CR＝CI／RI。若CR＜0.1，说明判别矩阵的同一性优良，判别矩阵的架构是合理的，无需调整。RI值见表4。

表4 平均任意同一性变量R I值

运用层次分析理论，我们可以对风力发电机中的变桨系统进行权重计算。在这个过程中，我们结合了定量计算和定性分析，对第二层的指标进行了全面的考虑。为了得到判断矩阵，我们综合了某风电场变桨系统近15月的实时监控数据和问题数据。表5为近15个月以来风机变桨系统发生的问题及故障汇总。

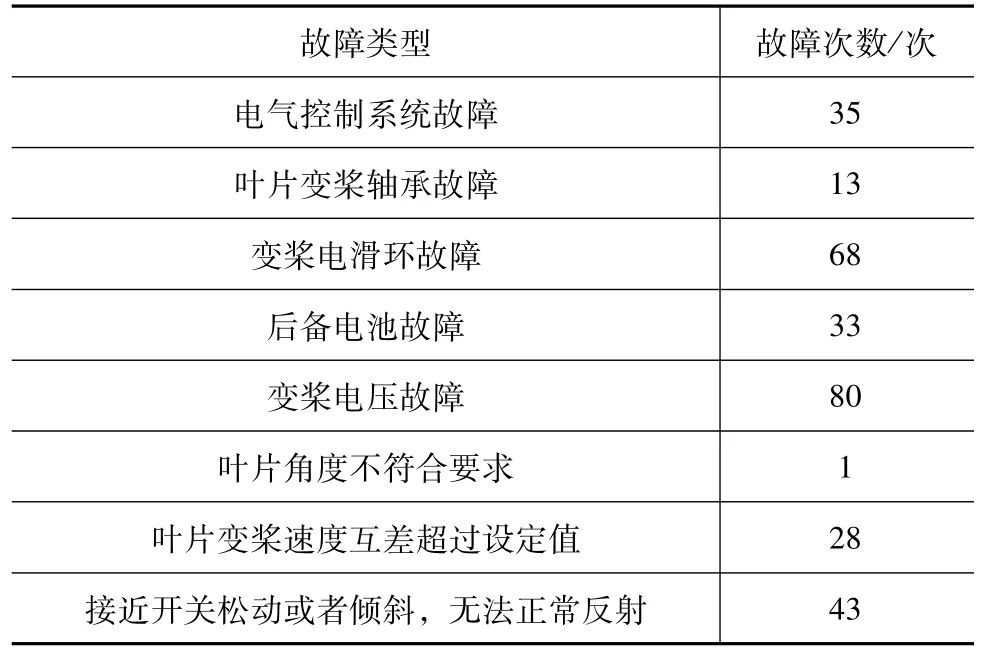
表5 变桨系统故障问题汇总

结合风场实际，对风机变桨系统所产生问题进行研判，得出以下7种指标。B1变桨发电机转速、B2变桨系统IGBT的温度、B3变桨系统的驱动电流、B4变桨系统的桨距角、B5变桨发动机温度、B6电网有功功率、B7变桨散热器温度。根据以上7种指标的重要性由强到弱可以排列为B4、B3、B2、B1、B5、B6、B7，构成矩阵见表6。

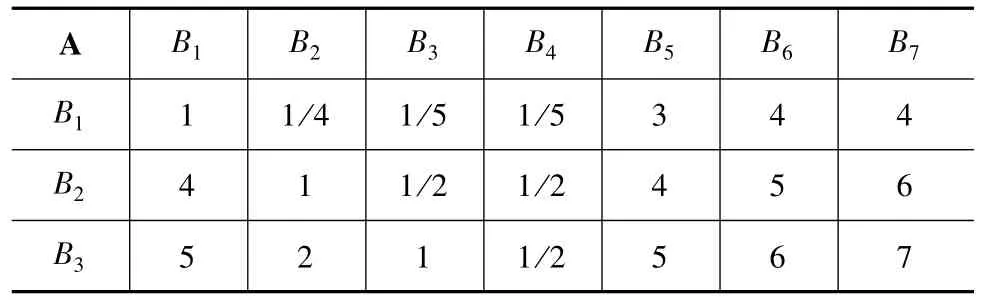
表6 目标层判别矩阵

4 变桨系统EXCEL权重计算

基于层次分析法的数据计算可以在EXCEL表格中进行计算得出相应的结果，图表明了干扰风机变桨系统不同变量权重的判断矩阵，并对同一性进行了判断。同一性比值CR为0.04895，小于0.1，判别矩阵的同一性优良。

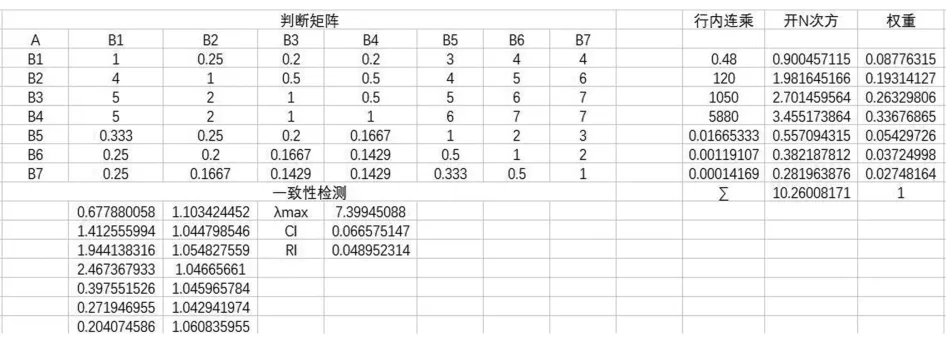
图 矩阵权重及一致性检验指标计算

通过层次分析法利用表格得到的权重结果见表7。

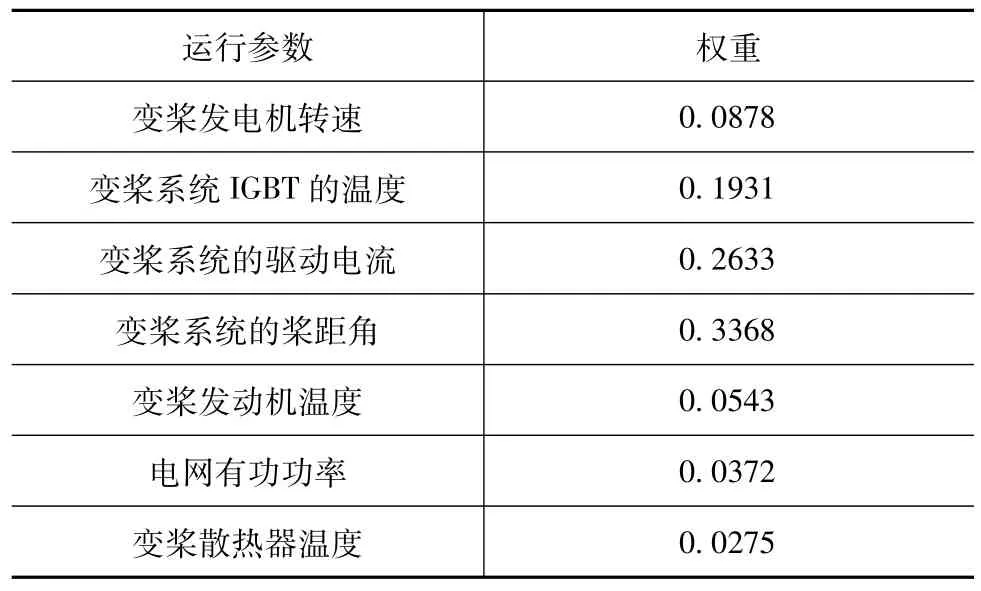
表7 变桨系统权重因素

5 结束语

通过表7的数据，运用层次分析理论对风机变桨系统的问题研判，可以得出以下结论：变桨系统的驱动电流、发电机转速、IGBT温度、桨距角这四个因素对风机变桨系统的权重共计0.881。这意味着此四项变量对变桨系统的潜在影响十分值得重视，所以在判断系统问题故障时，必须先行检测这些变量的异常情况。通过综合分析这些因素的权重，可以准确判断风电机组变桨系统的故障。

因此，为了准确诊断风电机组变桨系统的故障，应该密切关注这些参数的变化。在实际操作中，可以通过监控这些参数、定期检查设备状态、及时进行维修保养等措施来保障风电机组的正常运行。