基于多能源系统的微电网经济优化调度

郭晶晶

（国电南瑞吉电新能源（南京）有限公司）

0 引言

微电网（MG）可作为本地电源直接向负荷中心供电（孤岛模式）或连接到配电网。MG被认为是传统集中式网络问题的解决方案，直接位于负荷中心的小型发电厂的优势在于减少功率损耗、提高效率和减少供电干扰。可再生能源的使用对环境产生了良好的影响。多能源系统微电网（MESM）互联可增强系统抵御极端天气条件和自然灾害的能力，进而提高整个电网的稳定性。经济调度（ED）的目标是确定机组的最优调度，从而在满足运行约束的前提下使发电成本最小化［1-3］。本文提出了粒子群优化方法，用于解决MESM系统中发电机组和可再生能源的经济调度问题。在该方法中，根据可再生能源和发电机组参与的特性计算微电网经济成本。

1 多能源系统微电网模型

1.1 多能源系统微电网影响因素

在多能源系统微电网中，包括了不同能源的供应和利用，例如太阳能、风能、蓄电池能量等。为了实现微电网的经济优化调度，需要开发和应用合适的优化算法，如基于遗传算法、模糊控制、人工智能等方法，通过建立数学模型和优化目标函数，从而获得最优的能源调度策略［4-5］。

对于智能电网系统来说，协调MG和配电网之间的操作非常重要。此组合目的是通过能量交换和合作解决单个媒介或单个微电网无法解决的问题。通过经济优化调度策略，可以最大程度地提高多能源系统微电网的经济效益，降低能源的成本，提高能源利用效率，减少对主电网的依赖，实现能源的可持续发展。

1.2 目标函数

经济调度是指将负荷分配到每个发电机组上，以便获得能够以最佳成本满足负荷需求的组合发电机组，或者从发电机组合中找出输出功率的最佳值，目的是将发电总成本降至最低，并满足平等和不平等约束。在传统经济调度中，总发电量需满足总负载需求：

式中，PGi为第i台发电机产生的有功功率；PD为需求功率，可从发电机组的输入和输出特性中观察到。发电量受发电机组的最小和最大容量限制如下：

式中，PGimax、PGimin分别是发电机能力的上限和下限。成本函数FG可以通过如下所示的二次函数近似。

式中，FGi为第i个发电机的成本系数。

功率输出受到MG的最小和最大容量的限制，其能量来源如式（5）所示：

MG的总发电成本计算公式如下：

在式（8）中，当PMGj为正时，表示提供给电网的有功功率MGj，λj为MGj的销售价格；当PMGj为负时，表示从电网输出到MGj的功率，λj为MGj购买价格。

MG与MESM系统的互连将影响系统的操作，包括每个系统的负载分配发电机组。每个发电机组上的负荷分配基于成本最低的组合机组。MESM的总发电成本计算如下：

式中，FMESM、FMG、FG分别是系统运行的总成本、多能源系统分配的MG成本以及发电厂的成本。

1.3 约束条件

发电厂通常由装机容量超过数千兆瓦的大型天然气发电厂组成。容量为数十兆瓦或更大的发电机通常连接到电网并与电力系统合作。具有可再生能源的MG可以作为虚拟负荷以需求响应的形式参与调度系统，MG的发电厂必须首先满足自身的负荷。如果MG中的功率过剩，则MG向MESM系统供电。如果微电网系统不能满足其自身的要求，则从MESM系统获取功率。进入系统的MG参与调度MESM系统需考虑MG作为负载或发电机的特性。此外，还有一些研究者使用MG可再生能源。它必须根据历史数据和环境因素以及MG上的负载进行估计。因此，由于MG可再生能源的间歇性和当地负荷的随机性，MG输出在不同时期会发生变化，MG输出有时为正值，有时为负值。

2 经济优化调度算法

粒子群算法（PSO）指每个粒子由两个矢量Si和xi描述；在粒子群的每个移动步长中，每个粒子都由两个值更新。第一个值是粒子i的最佳先验位置，称为最好值pbi，并使用适应度函数进行计算。第二个值是所有pbi最好的粒子中最好的粒子，称为最好值gbi，任何粒子都会通过以下关系更新其新的速度和位置：

式中，c1、c2为加速度常数范围［0，2］；r1、r2为［0，1］范围内的均匀随机值；pbi表示粒子3i的最佳先验值；gbi表示pbi粒子里的最佳值；Si、xi分别表示粒子i的位置矢量和速度；k表示迭代次数；W表示惯性权重因子；iter表示当前迭代次数；Wmin、Wmax分别表示最小和最大惯性权重系数。

PSO算法步骤描述如下：

（1）读取数据系统和PSO参数，对象特征、数量粒子、种群大小、数量迭代、认知和社会参数以及约束因子。

（2）初始化，随机初始化速度和位置矢量。

（3）适应度评估，使用目标函数评估每个粒子的位置。

（4）记忆更新，更新了pbi和gbi，如式（10）所示：

（5）更新速度和位置，使用式（8）和（9）更新所有粒子的速度和位置矢量。

（6）终止过程，当达到最大代数时终止过程，如果终止条件不满足，则下一步是适应度评估。此过程持续重复，直到达到终止参数。

3 实例分析

该方法被应用于由四个发电机组和两个可再生能源的MG单元组成的微电网系统，构成MESM单线系统。MESM提供的每日负荷曲线如图1所示。

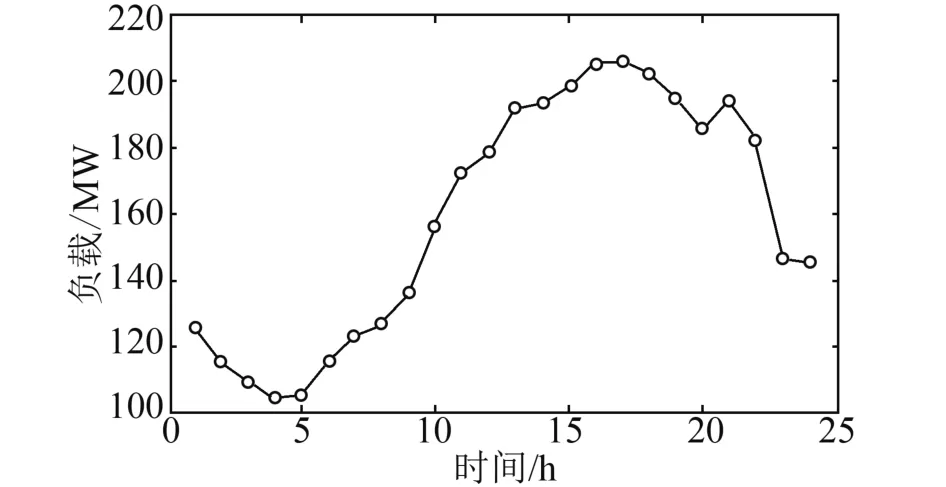
图1 MESM 系统日负载曲线

MG1和MG2具有可控和不可控功率输出。DG控制的功率输出容量分别为MG1和MG2的6MW 和8MW。不可控功率输出为MG1和MG2上光伏预测的功率输出。MG1和MG2是基于光伏的DG。因此，MG1为6：00～17：00的负载提供电力，MG2为7：00～18：00的负载提供电力。MG2的24h输出功率预测如图2所示。

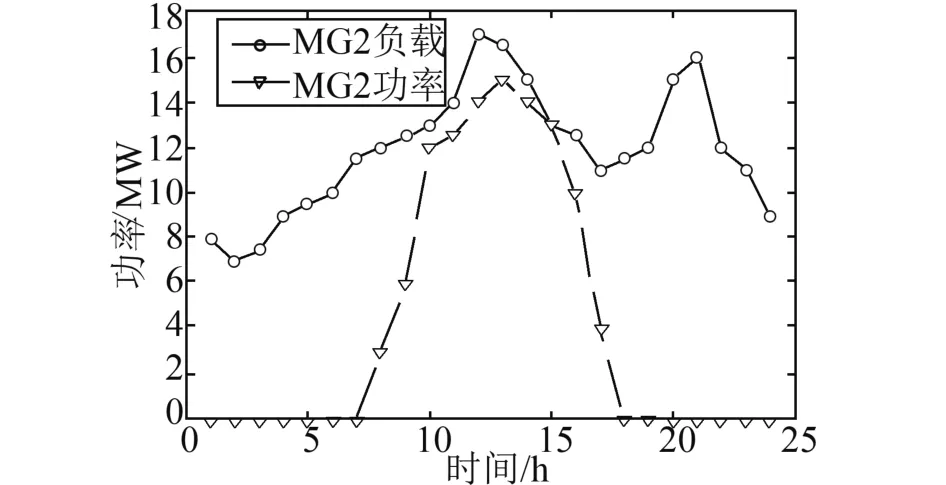
图2 MG2预测功率及负荷数据

当光伏输出功率和功率输出可控MG大于本地负载MG时，向系统供应电量。相反，在光伏输出功率和功率输出可控MG小于本地负载MG时，则购买电量。系统的MG1售价为135元／MW，MG2售价为140元／MW。从该系统购买MG1和MG2的价格为110元／MW。尽管购买价格低于出售价格，MG必须始终以其最大功率运行。本文将粒子群算法用于求解优化问题。迭代次数设置为1000，粒子数设置为500。使用本文中的粒子群算法。

图3显示了四个发电机组和两个基于MG的可再生能源（RES）功率的输出。图中显示了最便宜的发电机组分别是G2、G4、Gl和G3。发电机组的平均发电量为84.97%，尤其是在不可控MG2的情况下。G4、G1和G3机组的平均发电量分别为67.84%、43.18%和36.04%。G2和G4发电机组在16：00～19：00的时间段内达到最大发电量55MW，此时负荷仍然很大，而不可控发电机MG1和MG2开始下降。MG1在7：00～11：00的时间段内从发电机组获得电源，此时MG1的本地电源无法满足负载。在另一段时间内，MGl系统具有正值，这意味着MGl能够向系统（电网）出售电能。MG1可出售的总能量为135MW，购买量为19MW，因此24h内可节省1116MW。MG2始终为正值，这意味着在24h内，MG2能够满足本地负载，包括不可控MG2无法提供电源时。MG2在24h内向系统出售的总功率为182MW。

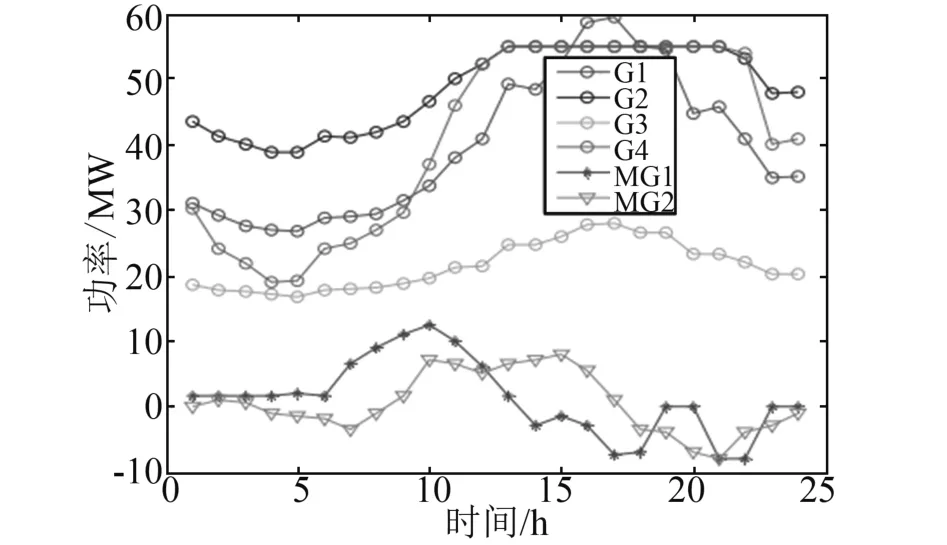
图3 发电机组及MG可再生能源24h功率

图4显示了含有和不含MG可再生能源系统的最低成本。在1：00～6：00的时间段内，使用和不使用MG的运营成本几乎相同。在7：00～16：00的时间段内，使用MG的运营成本比未使用MG低，而在17：00～24：00的时间段内，使用MG的运营成本比未使用MG高。总体而言，使用MG的系统的运行成本要低于没有使用MG的系统。不使用MG可再生能源的最低运营成本为50.8386万元，使用MG可再生能源的最低运营成本为50.1169万元。因此，使用MG可再生能源运行的微电网系统可降低运营成本7.2165万元。

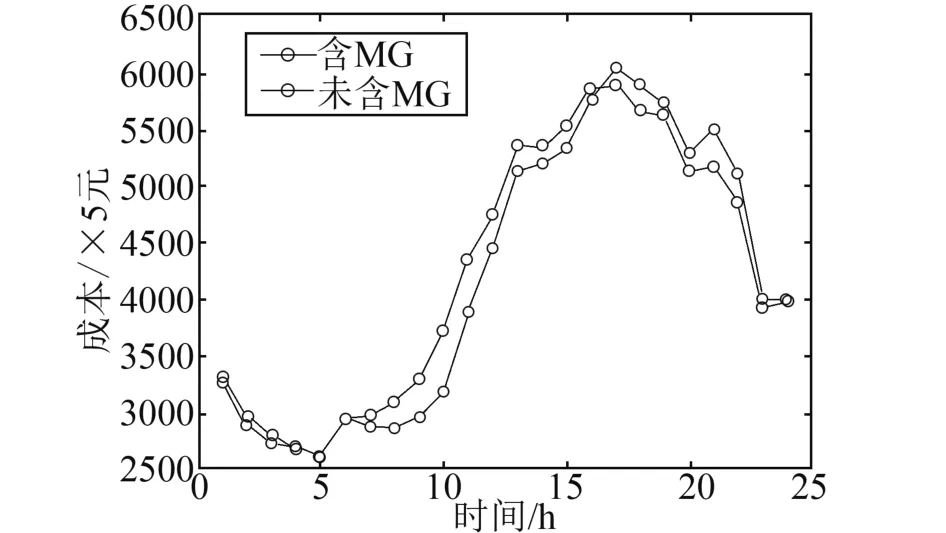
图4 MESM 系统在24h内的最小运行成本

4 结束语

本文将多组微电网与可再生能源微电网结合到MESM系统中，可以最大限度地减少发电机组或传统发电机的功率输出，并最大限度地提高微电网可再生能源的功率输出。未使用MG可再生能源时，最低运营成本为50.8386万元，使用MG可再生能源成本为50.1169万元，总共节省了7.2165万元的成本。使用MG可再生能源的MESM系统的运行成本低于未使用MG的运行成本，MESM系统最大限度地利用可再生能源实现微电网功率输出，并降低电力系统总体运营成本。