带后掠桨尖旋翼/螺旋桨的悬停气弹特性分析
黄薇 池骋

摘要 :针对旋翼/螺旋桨的大负扭和后掠桨尖设计在桨叶内部所带来的严重应力应变集中问题,结合三维结构动力学模型、旋翼气动模型和旋翼配平方法,对复合材料旋翼/螺旋桨进行了综合建模与气弹载荷分析,并通过悬停实验验证了综合模型的准确性。对比分析了无负扭、大负扭和大负扭带后掠桨尖的桨叶气弹特性,发现大负扭导致桨叶应力集中区域扩大,后掠桨尖使桨尖过渡区域的应力集中区域扩大,集中程度加剧。
关键词 :旋翼/螺旋桨;复杂几何外形桨叶;旋翼气弹耦合;三维桨叶力学模型;三维应力应变
中图分类号 :V214.1
DOI:10.3969/j.issn.1004132X.2024.02.001
开放科学(资源服务)标识码(OSID):
Analysis for Aero -elastic Characteristics of Prop-Rotor in Hover with a Swept Tip
HUANG Wei 1 CHI Cheng 2
1.School of Mechanical Engineering,Nanjing University of Science and Technology,
Nanjing,210094
2.Department of Aerospace Engineering,University of Maryland,College Park,USA,20742
Abstract : The issues of significant stress and strain concentration within the prop-rotor blades caused by large negative twist and swept tips were addressed herein. By 3D structural dynamics model, rotor aerodynamics model, and rotor trim methods, a comprehensive model of composite prop- rotor was developed, and the aeroelastic loads of composite prop-rotor were analyzed, and the accuracy of the synthesis model was validated through hover experiments. The analysis of aero-elastic characteristics was performed for rotor blades with zero twist, large negative twist, and large negative twist with swept tips. The results indicate that the large negative twist enlarges the stress concentration area, while the swept tip makes the stress concentration at the swept transition area larger and the degree of concentration worsens.
Key words : prop-rotor; complicated geometry blade; rotor aero-structural coupling; 3D structural blade model; 3D strain and stress
0 引言
倾转旋翼飞行器及电动城市空中交通旋翼飞行器都要求主升力系统能兼顾悬停与高速前飞两种工作状态。这种旋翼/螺旋桨的显著特点是展弦比小、负扭度大,在高速飞行时通常会因受到压缩效应带来的桨尖跨音速阻力的限制而不能进一步提高速度 [1] 。为延缓压缩效应,可添加后掠桨尖设计来提高飞行器性能。研究表明,后掠桨尖可以降低旋翼桨毂载荷、振动和气动噪声,提高倾转旋翼的飞行稳定性 [2-6] ,但会增大结构的复杂度和质量。为设计可靠、轻质、高性能的旋翼/螺旋桨,对旋翼桨叶结构进行精确建模和桨叶气弹载荷分析变得非常重要。
旋翼桨叶结构动力学建模研究的发展过程中,直到21世纪初,旋翼桨叶还是被抽象成一维的梁模型与提供剖面特性的二维模型的组合 [7-8] 。尽管梁模型在直升机工业中被广泛使用 [9-11] ,但并不是所有的桨叶结构都满足一维梁模型的基本假设。特别是桨叶的几何外形、内部结构和材料特性有较大或不连续变化时,或桨叶展弦比较小时,梁模型会出现不同程度的误差。EPPS等 [12] 测量了带后掠的梁的固有频率,发现梁的端部有大后掠角时,梁模型的精度会下降。带后掠桨尖的旋翼/螺旋桨是一种具有复杂几何外形的桨叶,使用梁模型分析气弹载荷并不能满足精度要求,故需要通过三维结构模型获得更准确的分析 结果。
JOHNSON等 [13] 指出了旋翼综合分析方法(包括适用于旋翼系统的三维结构模型综合分析方法)的发展方向。近年来,国外学者开始探索利用三维模型对旋翼桨叶进行综合分析。TRUONG [14] 对比了基于梁模型与商用三维有限元模型MSC/Marc的桨叶分析结果。YEO等 [15] 开展了基于梁模型的RCAS (rotorcraft comprehensive analysis system)软件与MSC/Marc的对比工作。KEE等 [16] 使用18节点六面体有限单元建立了桨叶的三维有限元模型。FILIPPI等 [17] 通过组合梁模型和三维有限元模型分析了后掠桨尖。上述研究都表明三维结构模型有助于提高复杂桨叶结构的分析精度。DATTA等 [18-19] 提出了旋翼桨叶的三维有限元结构分析方法,并将多体动力学整合到该三维有限元工具。STARUK等 [20-21] 初步搭建了基于计算机辅助设计(computer-aided design, CAD)的分析流程及工具,并使用旋翼三维有限元结构动力学工具对倾转旋翼进行分析。相比于梁模型,三维有限元结构模型不仅可以准确还原桨叶复杂的气动外形,还能描述桨叶内部复杂的结构和材料特性对桨叶动力学特性的影响。只有采用三维结构的动力学模型才能在气动载荷作用下直接分析具有复杂外形与结构的复合材料桨叶的应力应变场,從而避免过于保守的设计,优化飞行器的整体性能。这对先进旋翼/螺旋桨系统的结构轻量化设计与性能优化工作具有十分重要的意义。
旋翼桨叶的气弹耦合方法随气动模型与结构模型的发展而发展。气弹耦合的方法包括升力线模型与梁模型的耦合 [10,22] 、三维旋翼CFD模型与梁模型的耦合 [23-26] 、升力线模型与三维桨叶结构模型的耦合 [27] 。三维旋翼CFD模型与三维桨叶结构模型的耦合研究还在发展中 [28] ,虽然当前已有ANASYS、ABAQUS、Nastran等多种成熟的三维结构和气动建模商用软件,但旋翼系统的特殊性使得常用的商用软件并不适用于处理旋翼的气弹耦合问题。与固定翼气弹耦合问题相比,定常状态的旋翼系统都需要结合气动模型、结构模型和操纵配平进行可靠的分析。
本文针对具有后掠桨尖的复合材料旋翼/螺旋桨,重点分析其在悬停状态的气弹载荷。为对具有复杂气动外形与内部结构的桨叶进行高精度的建模,并全面分析其受载时的三维应力应变场,本研究结合了三维结构模型和旋翼气动模型。为验证旋翼模型的准确性,开展了悬停实验。为系统地分析大负扭与后掠桨尖对桨叶气弹载荷和应力应变的影响,针对悬停的工作状态,对无负扭矩形(straight untwisted, SUT)桨叶、 大负扭矩形(straight twisted, ST)桨叶和大负扭带后掠桨尖(swept twisted, SWT)桨叶进行了对比分析。
1 旋翼气弹响应分析模型
1.1 三维旋翼桨叶结构动力学模型
利用广义Hamilton原理建立三维桨叶结构动力学模型:
∫ t 2 t 1 ( δ U- δ T- δ W) d t=0 (1)
式中, δ U、 δ T、 δ W分别为势能项、动能项和外力项。
势能项采用Green-Lagrange应变和第二类Piola-Kirchhoff应力表示,这使得模型的张量分量在刚体运动过程中不变化,因此模型可用于分析具有大位移和大轉角的运动 [18] 。
采用六面体体单元将动力学方程进行离散,得到控制方程。为提高三维结构动力学模型对复杂桨叶结构的仿真精度,避免“单元锁闭” [29] 现象的发生,模型采用高阶的有限元体单元——27节点二阶Lagrangian等参数六面体单元。如图1所示,该单元有8个角节点、12个边节点、6个面节点和1个体节点。
通过 Hamilton 原理可得每个有限单元的质量矩阵 M e 、阻尼矩阵 C e 、刚度矩阵 K e 和载荷向量 F e 。依据单元之间的节点关系和边界条件的自由度可得桨叶总体的质量矩阵 M 、阻尼矩阵 C 、刚度矩阵 K 、载荷向量 F ,以及桨叶动力学方程 [30] :
Mq ¨ + Cq · + Kq = F (2)
式中, q 为桨叶有限元节点总体自由度向量。
式(2)中的矩阵均为 q 及其导数的函数,故该方程为非线性方程。
3种桨叶的基本参数如表1所示。常规直升机桨叶的展弦比为15、负扭约为12°,相比之下,表1中桨叶的展弦比小、负扭大,这使其更接近倾转旋翼飞行器的旋翼/螺旋桨桨叶。3种桨叶具有相同的半径、 弦长、根切与翼型。SUT桨叶与ST桨叶的差别是负扭角,SWT桨叶比ST桨叶多一个20°的后掠桨尖。
桨叶的翼型、材料和结构设计与选择都尽量接近真实旋翼。图2为桨叶的平面图。SUT桨叶、ST桨叶为矩形桨叶,且均具有-18.5°线性扭转;SWT桨叶在桨尖段(0.7 R ~1.0 R )上具有20°的后掠,直桨叶段与桨尖段之间有一个25.4mm长的过渡段,如图2b所示。SWT桨叶的直桨叶段、矩形桨叶的扭转相同;截面A-A、B-B相对于桨根的扭转分别为-11.6°和-17.1°,截面A-A和B-B间的扭转也是线性的。
3种桨叶都具有D型大梁(2层±45°平织的IM7/8552石墨纤维增韧环氧树脂复合材料)。大梁有1个根部连接件(7075铝合金)和4个前缘配重(钨合金棒),以及用于填充其余空间的泡沫芯(Rohacell IG-31)。桨叶的最外层为蒙皮(单层 ±45° 平织的IM7/8552石墨纤维增韧环氧树脂复合材料)。 桨叶大梁在0.7R(后掠段开始处)结束,因此桨叶具有2种剖面结构:有大梁的直桨叶段和无大梁的桨尖段,如图3所示。桨叶材料的实测属性列于表2、表3。
桨叶的参数化几何模型由三维CAD设计软件CATIA v5R20建立。如图4所示,大负扭后掠桨叶的几何模型对气动外形与内部结构(蒙皮、大梁、前缘配重等)都进行了精确表达。如图5所示,基于桨叶的几何模型使用网格预处理器Cubit [31] 生成尺寸大小不一的桨叶有限元网格单元。单元为27节点二阶Lagrangian等参数六面体单元,数量为2751。
上述复合材料桨叶三维结构动力学模型的准确性已被剖面结构特性、非旋转/旋转固有特性、真空条件中的旋转应变分布的实验验证 [32] 。本文在上述三维结构模型的基础上拓展,分析复合材料桨叶的气弹载荷特性。
1.2 气动力模型
本文采用升力线理论计算桨叶的气动力,将桨叶分为多个桨叶段,每段都用一个二维翼型剖面表示。每段的气动力和力矩受桨叶所处位置的动压与气动迎角影响,二维翼型的升力、阻力和俯仰力矩根据该剖面的气动迎角和马赫数,通过查表法插值计算得到。VR-7翼型的气动力系数通过二维计算流体力学分析得到,并使用实验数据对其零迎角阻力进行修正。本文的研究重点是分析悬停与轴流前飞状态的桨叶气弹载荷,故采用动量叶素理论和Prandtls桨尖损失系数 [1] 计算桨盘的诱导速度分布,以提高模型的计算效率。后掠桨尖对气动力的影响通过桨尖处马赫数的变化与气动中心的偏置体现。
1.3 气弹信息交互
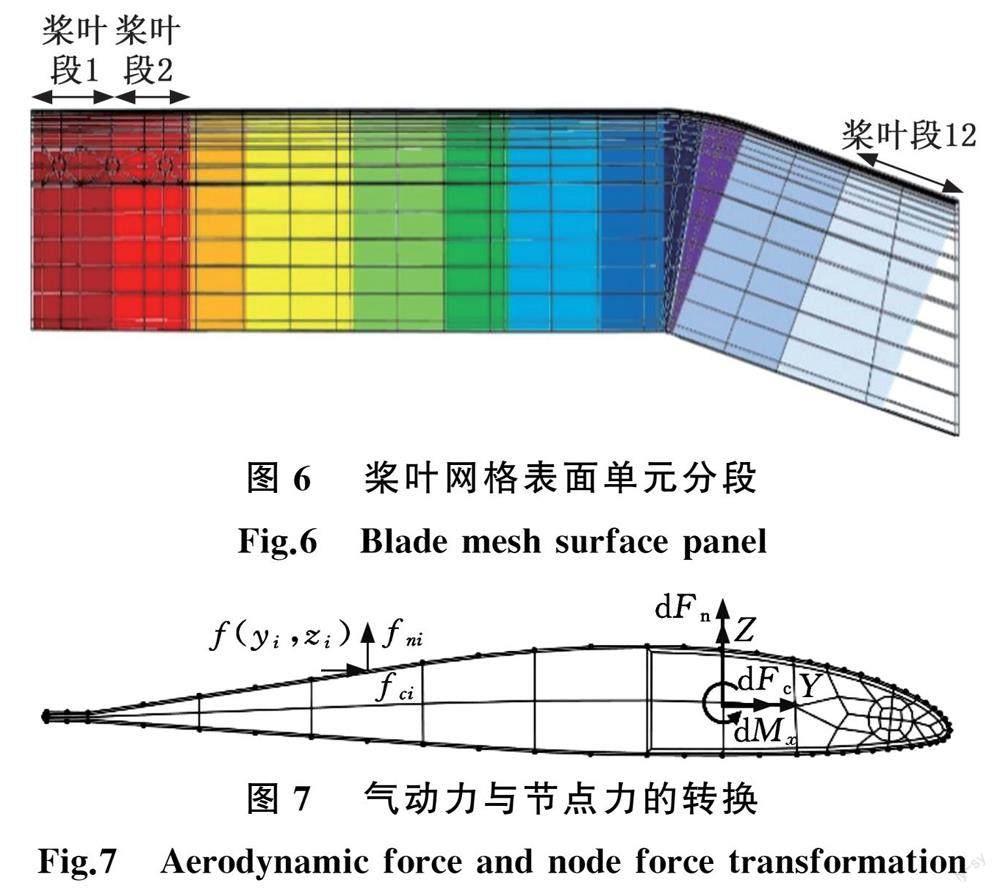
为分析气弹响应,算法必须实现结构模型与气动模型的信息交互。气弹信息交互的一个功能是将气动力施加到桨叶结构模型,即将桨叶段升力、阻力和力矩转换为作用在结构模型每个表面节点上的压力与切向力。将桨叶有限元网格的表面单元分成多个桨叶段,如图6所示,每个表面网格段都对应气动模型的一个桨叶段。每个桨叶段单位长度的垂向力、弦向力和力矩与表面网格对应节点的垂向力和弦向力的转换关系由该剖面的表面网格节点坐标决定 [24] ,如图7及下式所示。
d F n d F c d M x = n ∑y i 0 0 ∑z 2 i n ∑y i ∑(y 2 i-z 3 i) -∑z i a 1 a 2 a 3 (3)
f n i =a 1+a 2y i f c i =a 2z 2 i+a 3 (4)
式中,y i、z i分别为第i个节点的垂向坐标和弦向坐标;a 1、a 2和a 3为需要求解的系数;n为节点个数。
该转换关系能保证所有节点力的合力与力矩跟气动力与力矩一致。
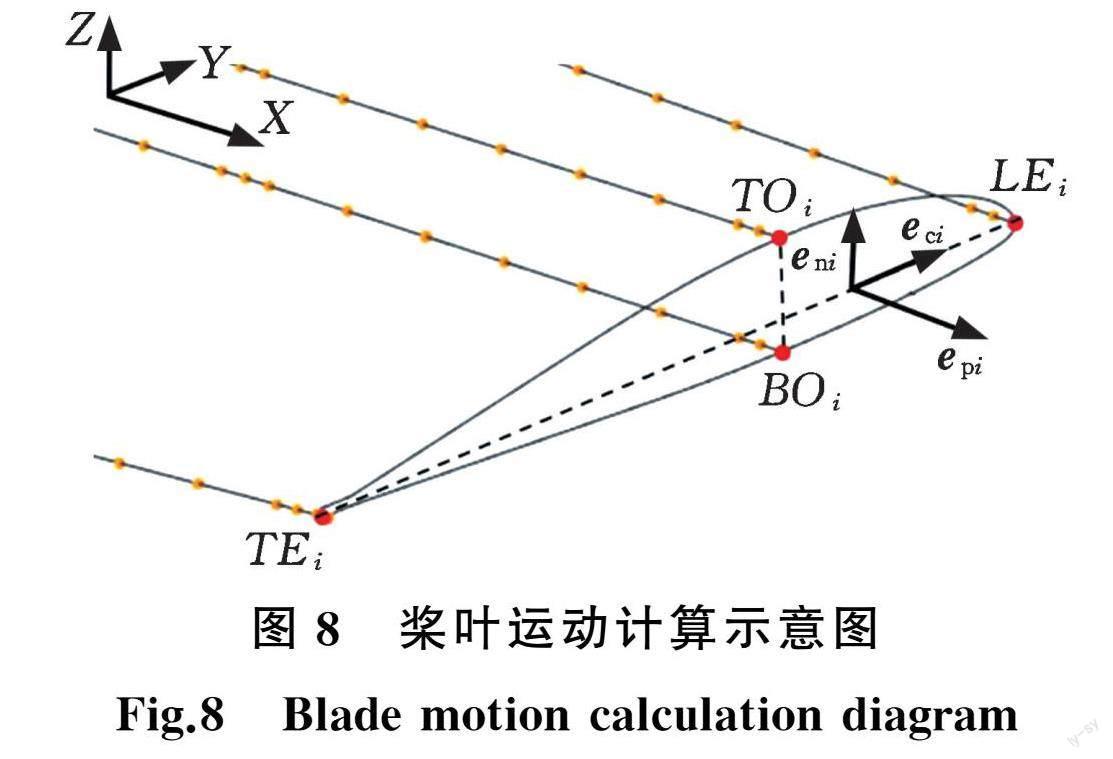
气弹信息交互的另一个功能是将桨叶的运动反馈到气动模型。桨叶结构模型的每一个剖面内都包括数百个节点,而气动模型只需将1/4弦长处的运动作为输入。为此定义4组节点(前缘节点LE i、后缘节点TE i、上表面节点TO i、下表面节点BO i)来确定第i 个剖面1/4弦长处的运动。如图8所示,通过上述4组节点的运动可计算每个桨叶剖面1/4弦长处的运动,并得到剖面的3个单位向量:垂向单位向量 e n i 、弦向向量 e c i 和法向向量 e p i 。通过这3个单位向量可以得到剖面的俯仰角,再结合桨叶1/4弦长处的运动速度和气流速度可计算出气动迎角。
1.4 悬停气弹响应求解
图9所示为桨叶气弹响应的求解流程。悬停状态下的桨叶气弹载荷分析可看作是一个定常状态问题,即桨叶受力平衡状态不随时间发生变化。为体现旋翼旋转带来的非线性效应,首先根据旋翼转速完成桨叶固有特性计算,获得该转速下的桨叶刚度矩阵。桨叶刚度矩阵由离心力主导,气动力引起的变形对刚度矩阵的影响较小,故在气弹迭代中停止刚度矩阵的更新,以提高计算效率。整个气弹响应的求解过程需对动力学模型、气动力模型、入流模型和旋翼配平进行迭代计算。迭代结束时,输出桨叶的气弹响应。
2 桨叶气弹模型的实验验证
为验证上述桨叶气弹模型,制作了SWT复合材料桨叶,搭建了悬停实验平台,利用实验测量了悬停状态下的旋翼性能和桨叶表面应变。
2.1 悬停实验系统
制作的SWT复合材料桨叶如图10所示。悬停实验中,桨叶桨距的调整通过无铰式桨毂的变距机构实现。如图11所示,无铰式桨毂由中心块、桨叶接头和连接螺钉组成。中心块和桨叶接头通过3个螺钉连接,中间螺钉是变距轴螺钉,桨叶接头以该螺钉为轴进行变距;两侧的螺钉负责固定桨叶桨距。3个螺钉共同承受桨叶的载荷并将其传递到桨毂中心块上。为尽可能保持桨毂结构的紧凑性,3个螺钉都紧挨着桨叶根部。
旋翼性能通过旋翼扭矩和拉力确定。旋翼扭矩使用安装在旋翼轴上的扭矩传感器测量,如图12所示。旋翼轴扭矩的测量采用由2个双栅剪切应变片(Omega engineering, SGT-2DC/350-SY43)组成的全桥电路完成,该电路可以放大旋翼扭矩产生的信号,并抑制其他载荷的影响。
旋翼拉力和桨毂力矩的测量通过自主设计的三分量天平完成,其中,测量桨毂力矩是为了检查旋翼是否处于悬停状态。如图13所示,天平的测量元件由4个单自由度力传感器组成,通过4个传感器测得的力和它们之间的位置关系计算旋翼产生的拉力与桨毂力矩。 实验前,对天平进行标定,以达到实验要求。将整个旋翼试验台台体固定在天平的试验台安装板上,形成单一的传力路径。
旋翼气动模型只分析了桨叶的气动力,所以在悬停实验中应该尽量减小桨叶以外物体对流场的影响。为此,在实验中使用整流罩包裹旋翼以外的整個试验台。旋翼试验台固定在图14所示的悬停实验塔上,桨盘平面与地面的距离达到 2.3 m, 在避免地面效应的同时提高实验的安全 系数。
桨叶表面应变通过三轴等角应变花(Micro-measurements, C5K-09-S5198-350-33F)测量,如图15所示。该应变花可测量轴向正应变 ε 11 、横向正应变 ε 22 和面内切应变(工程应变) γ 12 。每片桨叶都有4个测量点,测点1~4的径向位置依次为 0.55R、0.65R、0.73R和0.85R。
2.2 悬停实验验证
实验测量了SWT桨叶在旋翼转速500~3000 r/min下的拉力、扭矩及桨叶表面应变。实验时的环境温度为21.1 ℃,气压为9953 Pa。图16所示为旋翼功率系数 C P 随旋翼桨叶载荷系数 C T 的变化,其中,旋翼实度 σ =0.133。由图16可以看出,旋翼功率的计算值与实测值都随桨叶载荷系数的增大而增大。旋翼性能的计算值与其实测值基本吻合,这说明本文采用的旋翼气动模型可以体现旋翼/螺旋桨在悬停中的总体气动特性。
通过测量悬停状态下的桨叶表面应变来验证气动模型与结构模型间信息交互方法的有效性。图17为SWT桨叶以4°总距(0.75 R 处)悬停时的应变实测值与计算值的对比图,可以看出,桨叶上各个位置应变的计算值都与实验测量值有较好的一致性。轴向正应变 ε 11 的预测比横向正应变 ε 22 和面内切应变 γ 12 的预测更准确。三种桨叶中,SWT桨叶具有最复杂的外形与结构。该桨叶的计算值与实验测量值的一致性充分验证了旋翼气动模型、桨叶结构模型和气弹信息交互方法的准确性。
由图17还可以看出,各个测量位置的应变都随旋翼转速的增加而增大,这说明悬停状态中的旋翼桨叶载荷以离心力为主导,但1号位置的应变并没有明显大于其他更靠近桨尖位置的应变。这是由于测量位置都在桨叶上表面,在升力的作用下,桨叶上表面会受到压缩,部分抵消离心力带来的拉伸作用。
3 悬停状态桨叶气弹载荷分析
运用前文所述的模型对悬停状态下的旋翼/螺旋桨桨叶气弹载荷进行分析。悬停时,旋翼前进比 μ 与入流比 λ 均为零,桨尖马赫数为0.66。将 C T =0.11作为配平目标,将总距 θ 75 作为操纵量对旋翼进行配平。配平后,SUT、ST和SWT桨叶旋翼的总距分别为11°、10.4°和10.4°。
3.1 气动力分布
图18~图20所示为悬停状态下桨叶的垂向气动力系数 C n、弦向气动力系数 C c和气动力矩系数 C m的分布,可以看出,SUT桨叶的垂向和弦向气动力分布都更集中在靠近桨尖的位置,桨叶负扭的加入使得ST桨叶和SWT桨叶的垂向与弦向气动力沿展向的变化相对平缓,后掠桨尖只导致气动力系数的幅值产生轻微的减小。在气动力矩方面,3种桨叶的径向分布差异不大。
3.2 桨根结构载荷
图21所示为径向位置 R /4的桨叶结构载荷(扭转力矩 M x、挥舞弯曲力矩M y、摆振弯曲力矩M z ),可以看出,负扭和后掠桨尖都使桨叶的扭转力矩增大。负扭对挥舞弯曲力矩的影响很小,但后掠桨尖使桨叶的挥舞弯曲力矩有较大的增长。后掠桨尖带来的挥舞弯曲力矩增长是因为后掠角使桨尖重心处于旋转平面以下,带来额外的弯矩。负扭和后掠桨尖对摆振弯曲力矩的影响都很小。
3.3 桨叶应力分布
通过三维结构模型可对所有应力应变分量进行分析,但本文重点分析轴向应力、面内切应力和层间应力。
图22所示为桨叶的轴向应力分布,结果显示,轴向应力由桨叶蒙皮和大梁共同承受,并集中在桨叶下表面蒙皮与大梁后缘的交界处;桨叶前缘有较大的轴向应力。这种应力分布是桨叶升力和阻力带来的挥舞和摆振弯曲力矩导致的。钨合金前缘配重出现很大的应力。ST桨叶表面的轴向应力幅值较大区域的位置与SUT桨叶基本一致,但是其范围更大。桨叶大梁在0.7 R 处结束,其结构变化导致的刚度突变使得应力出现集中现象。与SUT桨叶、ST桨叶相比,SWT桨叶的应力分布有明显的变化。后掠角使得桨尖段的重心位置大幅度偏置,偏置重心的离心力产生额外的弯曲力矩,所以SWT桨叶前缘的桨尖过渡段并没有ST桨叶的应力集中,后缘的轴向应力显著增大,但应力增大的区域并不局限于桨叶后缘的后掠转角处,而是覆盖了整个桨叶的中段。
图23所示为桨叶的面内切应力分布。与轴向应力不同,面内切应力基本上完全由桨叶蒙皮承受。除桨根区域外,SUT桨叶的面内切应力集中在大梁结束处的外侧。ST桨叶的高面内切应力区域向大梁结束处内侧靠后缘的位置蔓延。桨叶结构加入后掠桨尖后,SWT桨叶的面内切应力集中区域覆盖了整个后掠桨尖段的前缘和部分 后缘。
桨叶是由多层复合材料及其他材料粘合成的整体。桨叶受载发生变形时,各材料的变形可能不一致,这导致复合材料各层之间或复合材料与其他材料之间产生层间应力。圖24为桨叶的层间应力分布图。层间应力只存在于桨叶内部,所以图24没有展示桨叶表面的应力分布。层间应力是靠复合材料基体承受的,而基体的强度一般较低,所以即便图24中的层间应力幅值很小,但在分析中还应给予关注。由图24可以观察到,层间应力主要出现在靠近桨根前缘和桨尖过渡段的大梁后缘。3种桨叶层间应力出现的位置基本一致,但SWT桨叶有相对较大的幅值。
综上所述,若旋翼/螺旋桨的结构设计侧重于悬停状态的优化,则有大负扭和大后掠桨尖的桨叶应在无负扭矩形桨叶的基础上加强整个桨叶后缘、桨根段和桨尖段的桨叶前缘,以及桨尖过渡位置的大梁后缘。
4 结论
(1)对比悬停验证实验的数据可知,本文旋翼模型计算的旋翼拉力、旋翼功率和桨叶应变都有良好的吻合度。这表明本文的桨叶三维结构模型、气动力模型及信息交互方法都是可靠的,可以综合分析不同工作状态下的负扭和后掠桨尖对复合材料桨叶的影响。
(2)悬停状态中,负扭使桨叶的气动力分布相对均匀,但在离心力和气动力的共同作用下,大负扭导致桨叶应力集中区域扩大。
(3)在悬停状态中,后掠桨尖带来的气动中心和重心偏置使桨尖过渡区域的应力集中区域扩大,集中程度加剧。
(4)需要在桨叶中加入负扭和后掠桨尖来优化旋翼时,应当加强整个桨叶的后缘、桨根/桨尖段的前缘、桨尖过渡段的大梁后缘。
参考文献 :
[1] LEISHMAN G J. Principles of Helicopter Aerodynamics[M]. New York:Cambridge University Press, 2006: 292-295.
[2] YEN J G. Effects of Blade Tip Shape on Dynamics, Cost, Weight, Aerodynamic Performance, and Aeroelastic Response[J]. Journal of the American Helicopter Society, 1994, 39(4): 37-45.
[3] 虞志浩, 杨卫东, 张呈林. 基于Broyden法的旋翼多体系统气动弹性分析[J]. 航空学报, 2012, 33(12): 2171-2182.
YU Zhihao, YANG Weidong, ZHANG Chenglin. Aeroelasticity Analysis of Rotor Multibody System Based on Broyden Method[J]. ACTA Aeronauticaet Astronautica Sinica, 2012, 33(12): 2171-2182.
[4] SRINIVAS V, CHOPRA I, MARK W N. Aeroelastic Analysis of Advanced Geometry Tiltrotor Aircraft[J]. Journal of the American Helicopter Society, 1998, 43(3): 212-221.
[5] ZHAO Q J, GUO H X. A Study on Aerodynamic and Acoustic Characteristics of Advanced Tip-shape Rotors[J]. Journal of the American Helicopter Society, 2007, 52(3): 201-213.
[6] ACREE C W. Effects of V-22 Blade Modifications on Whirl Flutter and Loads[J]. Journal of the American Heli-copter Society, 2005, 50(3): 269-278.
[7] HOUBOLT J C, BROOKS G W. Differential Equations of Motion for Combined Flapwise Bending, Chordwise Bending, and Torsion of Twisted Nonuniform Rotor Blades[R]. NASA, TR-1346, 1957.
[8] HODGES D H, DOWELL E H. Nonlinear Equations of Motion for the Elastic Bending and Torsion of TwistedNonuniform Rotor Blades[R]. NASA, TN-D-7818, 1974.
[9] CHOPRA I, NGUYEN K. Development of UMARC (University of Maryland Advanced Rotor Code)[C]∥The 46th Annual Forum of the American Helicopter Society. Washington D C, 1990:46-1-004.
[10] JOHNSON W. Rotorcraft Aerodynamics Models for a Comprehensive Analysis[C]∥The 54th annual Forum of the American Helicopter Society. Washington D C, 1998:54-00103.
[11] SABERI H, KHOSHLAHJEH M, ORMISTON R A, et al. Overview of RCAS and Application to Advanced Rotorcraft Problems[C]∥American Helicopter Society 4th Decennial Specialists Conference on Aeromechanics. San Francisco, 2004:sm-aeromech-2004-0043.
[12] EPPS J J, CHANDRA R. The Natural Frequencies of Rotating Composite Beams with Tip Sweep[J]. Journal of the American Helicopter Society, 1996, 40(1): 29-36.
[13] JOHNSON W, DATTA A. Requirements for Next Generation Comprehensive Analysis of Rotorcraft[C]∥American Helicopter Society Specialists. San Francisco, 2008:sm-2008-mech-037-Johnson.
[14] TRUONG V K. Dynamics Studies of the ERATO Blade, Based on Finite Element Analysis[C]∥The 31st European Rotorcraft Forum. Florence, 2005:94.
[15] YEO H, TRUONG K V, CHANDRA R. Comparison of One-dimensional and Three-dimensional Structural Dynamics Modeling of Advanced Geometry Blades[J]. Journal of Aircraft, 2014, 51(1): 226-235.
[16] KEE Y J, SHIN S J. Structural Dynamic Modeling for Rotating Blades Using Three Dimensional Finite Elements[J]. Journal of Mechanical Science and Technology, 2015, 29(4): 1607-1618.
[17] FILIPPI M, ZAPPINO E, CARRERA E. Multidimensional Models for Double-Swept Helicopter Blades[J]. AIAA Journal, 2019, 57(6): 2609-2616.
[18] DATTA A, JOHNSON W. Three-dimensional Finite Element Formulation and Scalable Domain Decomposition for High Fidelity Rotor Dynamic Analysis[C]∥American Helicopter Society 65th Annual Forum Proceedings, Grapevine, 2009:65-2009-000330.
[19] DATTA A, JOHNSON W. A Multibody Formulation for Three Dimensional Brick Finite Element Based Parallel and Scalable Rotor Dynamic Analysis[C]∥American Helicopter Society 66th Annual Forum, Phoenix, 2010:66-2010-000246.
[20] SRARUK W, CHOPRA I, DATTA A. Three-dimensional CAD-Based Structural Modeling for Next Generation Rotor Dynamic Analysis[C]∥ American Helicopter Society 70th Annual Forum. Quebec, 2014:70-2014-0038.
[21] SRARUK W, DATTA A, CHOPRA I, et al. An Integrated Three-dimensional Aeromechanics Analysis of the NASA Tilt Rotor Aeroacoustic Model[J]. Journal of the American Helicopter Society, 2018, 63(3): 1-12.
[22] 楊卫东, 张呈林, 王适存. 后掠桨尖旋翼气弹响应及载荷分析[J]. 南京航空航天大学学报, 1998 , 30 (1): 52-58.
YANG Weidong, ZHANG Chenglin, WANG Shicun. Response and Loads Analysis of Helicopter Rotor Blades with Swept Tips[J]. Journal of Nanjing University of Aeronautics and Astronautics, 1998, 30 (1): 52-58.
[23] 王俊毅, 招启军, 肖宇. 基于CFD/CSD耦合方法的新型桨尖旋翼气动弹性载荷计算[J]. 航空学报, 2014, 35(9): 2426-2437.
WANG Junyi, ZHAO Qijun, XIAO Yu. Calculations on Aeroelastic Loads of Rotor with Advanced Blade-tip Based on CFD/CSD Coupling Method[J]. Acta Aeronauticaet Astronautica Sinica, 2014, 35(9): 2426-2437.
[24] 马砾, 招启军, 赵蒙蒙,等. 基于CFD/CSD耦合方法的旋翼气动弹性载荷计算分析[J]. 航空学报, 2017, 38(6): 1-14.
MA Li, ZHAO Qijun, ZHAO Mengmeng, WANG Bo. Computation Analyses of Aeroelastic Loads of Rotor Based on CFD/CSD Coupling Method[J]. Acta Aeronauticaet Astronautica Sinica, 2017, 38(6): 1-14.
[25] DATTA A,NIXON M, CHOPRA I. Review of Rotor Loads Prediction with the Emergence of Rotorcraft CFD[J]. Journal of the American Helicopter Society. 2007, 52 (4): 287-317.
[26] DATTA A, CHOPRA I. Prediction of UH-60 Main Rotor Structural Loads Using CFD/Comprehensive Analysis Coupling[J]. Journal of the American Helicopter Society, 2008, 53 (4): 351-365.
[27] DATTA A. X3D—a 3D Solid Finite Element Multibody Dynamic Analysis for Rotorcraft[C]∥American Helicopter Society Technical Meeting on Aeromechanics Design for Vertical Lift. San Francisco, 2016: 20-22.
[28] PATIL M, ARIAS P, BAEDER J, et al. An Integrated Three-dimensional Aeromechanical Analysis of Lift Offset Coaxial Rotors[C]∥The Vertical Flight Societys 78 th Annual Forum. Fort Worth, 2022:F-0078-2022-17518.
[29] BABUSKA I, SURI M. On Locking and Robustness in the Finite Element Method[J]. SIAM Journal on Numerical Analysis, 1992, 29(5): 1261-1293.
[30] BATHE K J. Finite Element Procedures[M]. Watertown:Prentice-Hall, Pearson Education, Inc., 2006.
[31] BLACKER T D, OWEN S J, STATEN M L, et al. CUBIT Geometry and Mesh Generation Toolkit 15.2 User Documentation[M]. Albuquerque:Sandia National Laboratories, 2016.
[32] CHI C, DATTA A, CHOPRA I, et al. Three-dimensional Strains on Twisted and Swept Composite Rotor Blades in Vacuum[J]. Journal of Aircraft, 2021, 58(1): 1-16.
( 編辑 张 洋 )
作者简介 :
黄 薇 ,女,1991年生,讲师。研究方向为结构动力学、结构优化设计。发表论文10余篇。 E-mail: huangwei91@njust.edu.cn。
池 骋 (通信作者),男,1990年生,助理研究员。研究方向为旋翼动力学。发表论文8篇。E-mail:chi@umd.edu。

