黄土高速铁路路基注浆扩散范围模型试验研究
温 浩,张先军,蔡德钩,岳 茂,于佳琪,瞿立明
(1.西南交通大学 土木工程学院,四川 成都 610031;2.中国国家铁路集团有限公司 工程管理中心,北京 100844;3.中国铁道科学研究院集团有限公司 铁道建筑研究所,北京 100081;4.西南交通大学 地球科学与环境工程学院,四川 成都 611756)
黄土在我国西北地区广泛分布,作为区域性特殊土,黄土具有湿陷性、水敏性等特点,黄土病害整治一直以来都是工程界关注的重点[1]。随着我国经济建设的发展,黄土地区铁路建设迅速发展,宝兰、郑西、大西等铁路线的建设对黄土高速铁路(以下简称“高铁”)路基的建设提出了更高的要求。黄土结构存在大孔隙、垂直节理等特征,在干燥时,黄土强度较高,但在降雨、振动等外界作用时强度降低,存在沉降等病害问题[2]。注浆加固技术作为路基病害整治技术,在软土地区应用广泛[3],但由于黄土力学性能复杂,注浆技术参数难以获得,最优的注浆方案不易确定。因此,黄土高速路基注浆技术参数亟待开展系统、深入的研究。
高铁路基沉降控制一直都是研究的热点[4-5],众多学者对注浆加固技术展开了研究。周文皎等[6]、张玉芳等[7]开展钢花管分段注浆现场原型试验,研究表明注浆形成的“树根状”加固体有效提高了周围土体的抗剪强度。陶伟明等[8]对聚氨酯复合注浆材料的研究表明其在富水砂砾地层的封堵及抗冲刷性能优异。黄大维等[9]开展隧道侧部注浆模型试验,发现注浆扩散模式可分为渗透-挤密-劈裂、挤密-劈裂-渗透两种。罗小博等[10]开展西北湿陷性黄土地基劈裂注浆现场试验,研究表明注浆加固后的地基承载力提高近3倍。王腾[11]基于D-P修正准则,给出适用于湿陷性黄土劈裂注浆注浆压力计算方法。马连生等[12]基于断裂力学,给出了黄土劈裂注浆过程中裂纹扩展方式。汪优等[13]基于FLAC-PFC耦合方法对盾构施工壁后注浆过程进行数值仿真,研究表明盾尾注浆对地表沉降控制有显著效果。Zhang等[14]使用PFC2D对黄土注浆扩散过程进行模拟,研究表明最终形成的浆脉呈Y形。Li等[15]基于连续扩散凝固数值仿真(SDS)方法,对不同流速下浆液扩散过程进行模拟。Yan等[16]基于FDEM,对裂隙岩体注浆过程中浆液迁移、浆液-岩体相互作用、裂缝扩展进行研究。综上所述,已有研究表明注浆加固可以有效提升土体强度,对注浆过程中浆液扩散模式也有较多研究,但对浆液扩散过程中关键参数的研究较少。
基于此,本文基于黄土高铁路基注浆模型试验,使用Edem-Fluent耦合技术进行注浆数值仿真。对黄土高铁路基注浆扩散范围及盲区进行研究,为黄土高铁路基设计参数的确定提供指导。
1 工程背景
大同—西安客运专线,线路全长853 km,是西部铁路重点建设工程[1]。本文以K276+066—K276+146里程处发生不均匀沉降病害的黄土路基为研究对象。既有路基自上而下依次为级配碎石、改良土、三七灰土,厚度均为0.5 m。该段自2015年7月出现下沉,累计最大沉降达50 mm以上。动力触探等表明道心、路肩存在地层不密实的情况。
2 模型试验概况
2.1 试验原材料
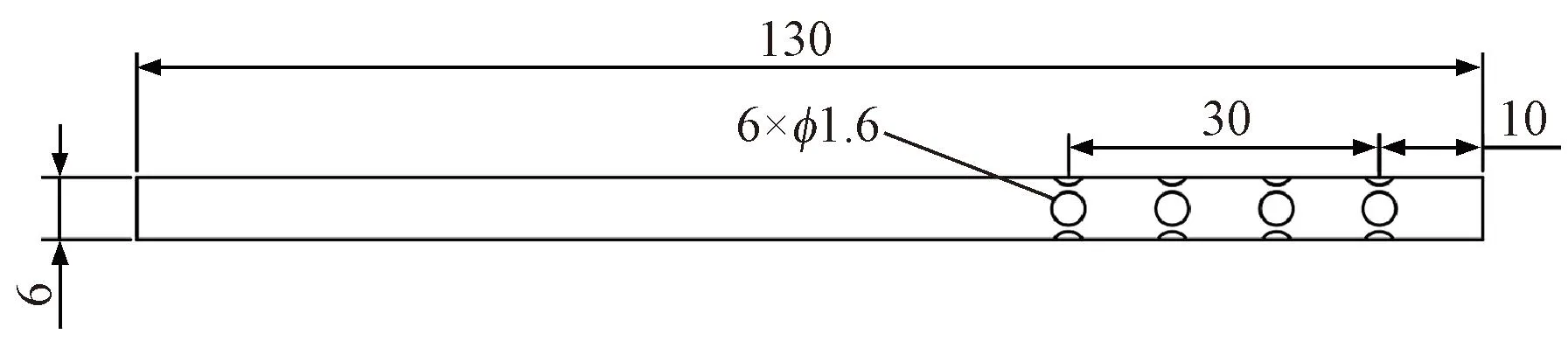
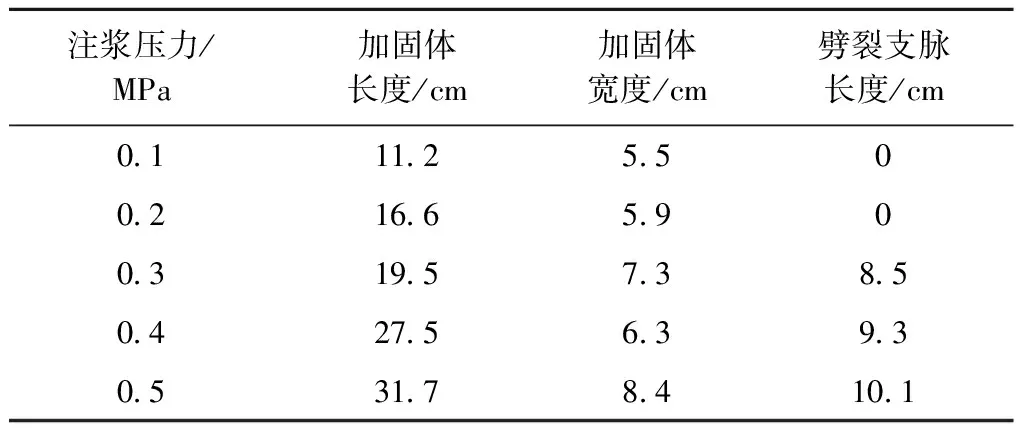
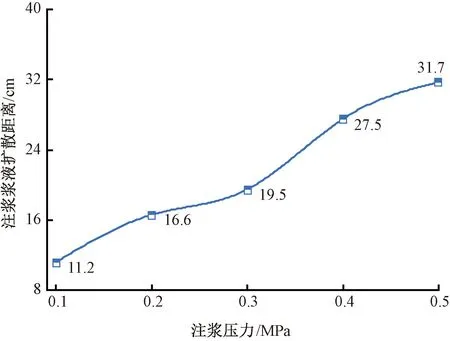
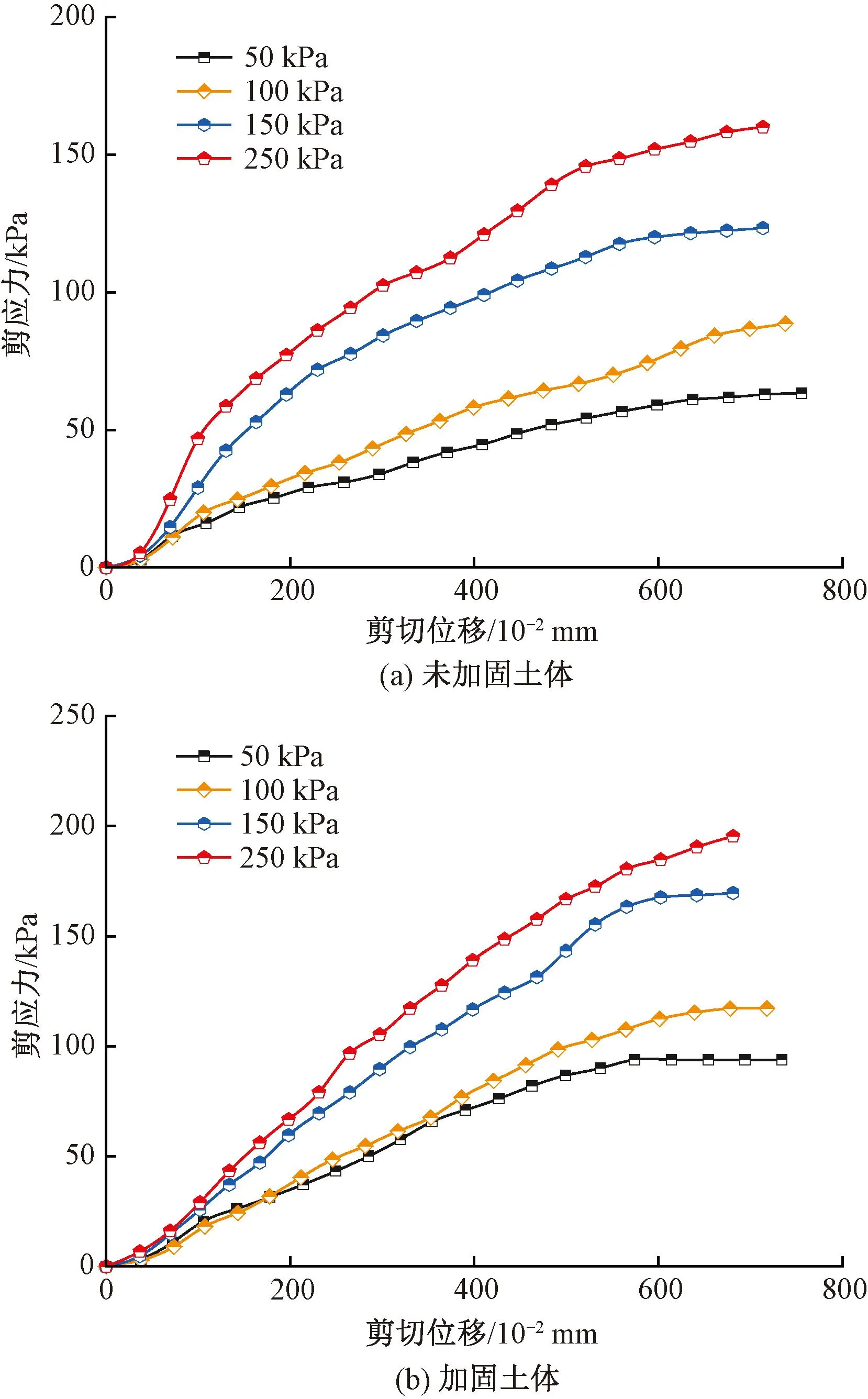
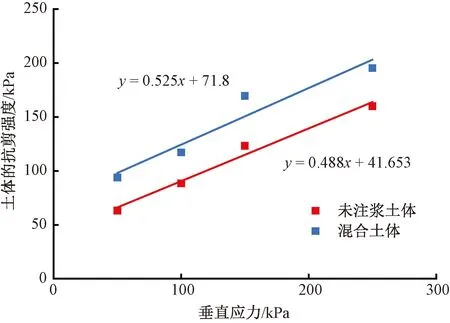
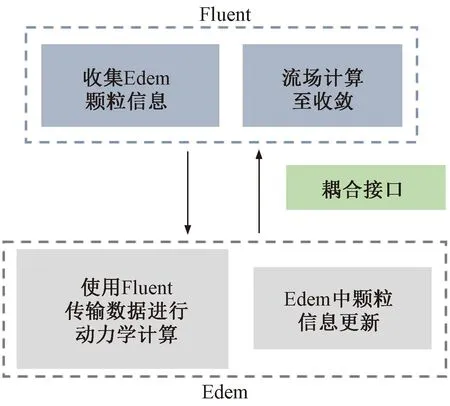
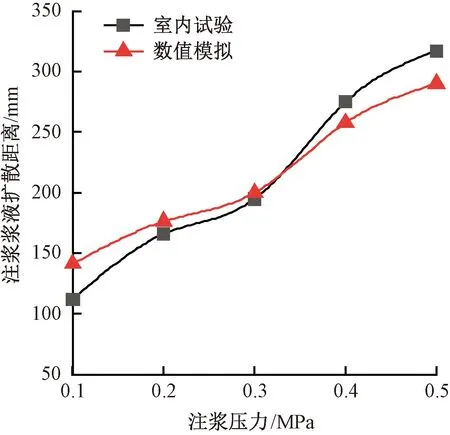
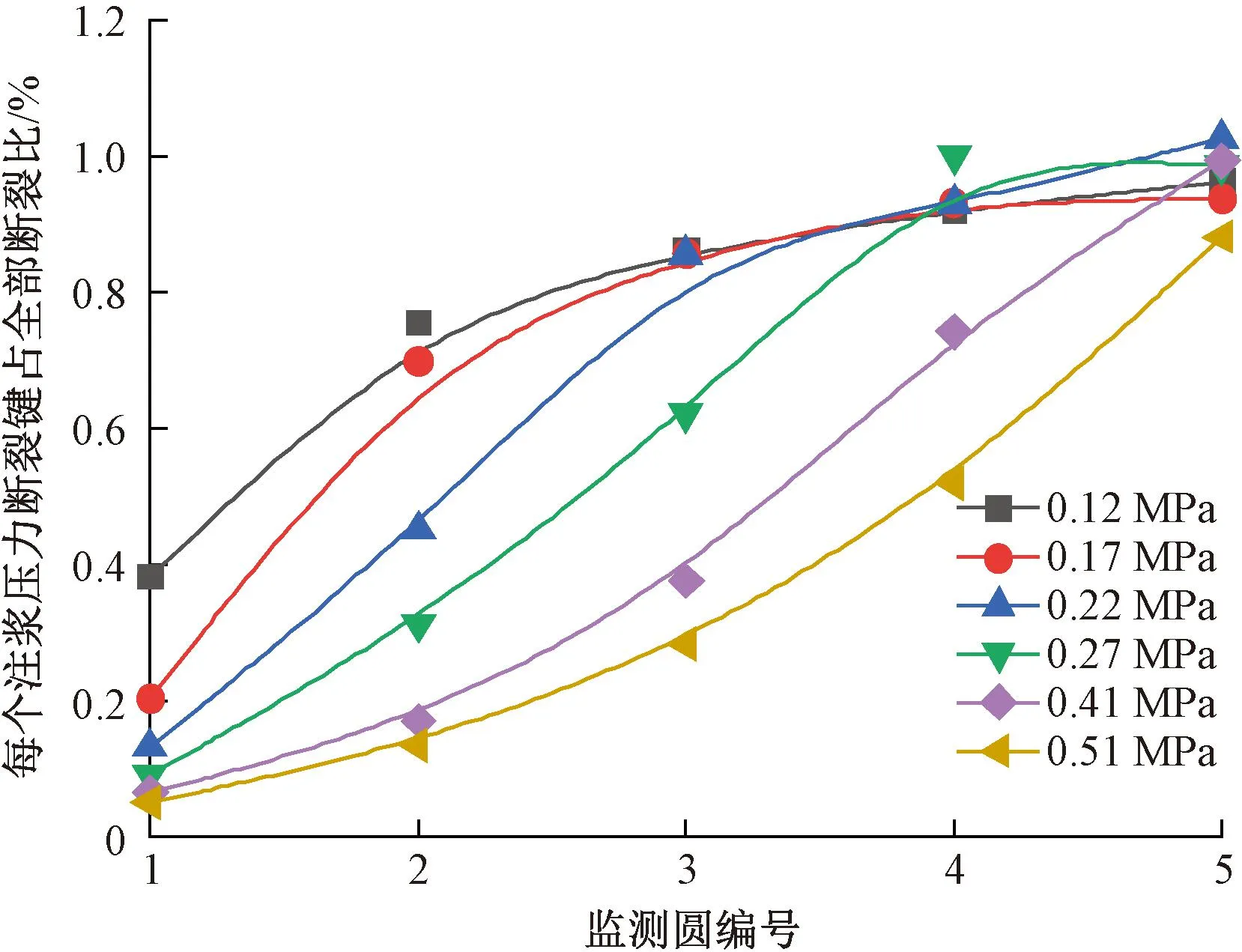
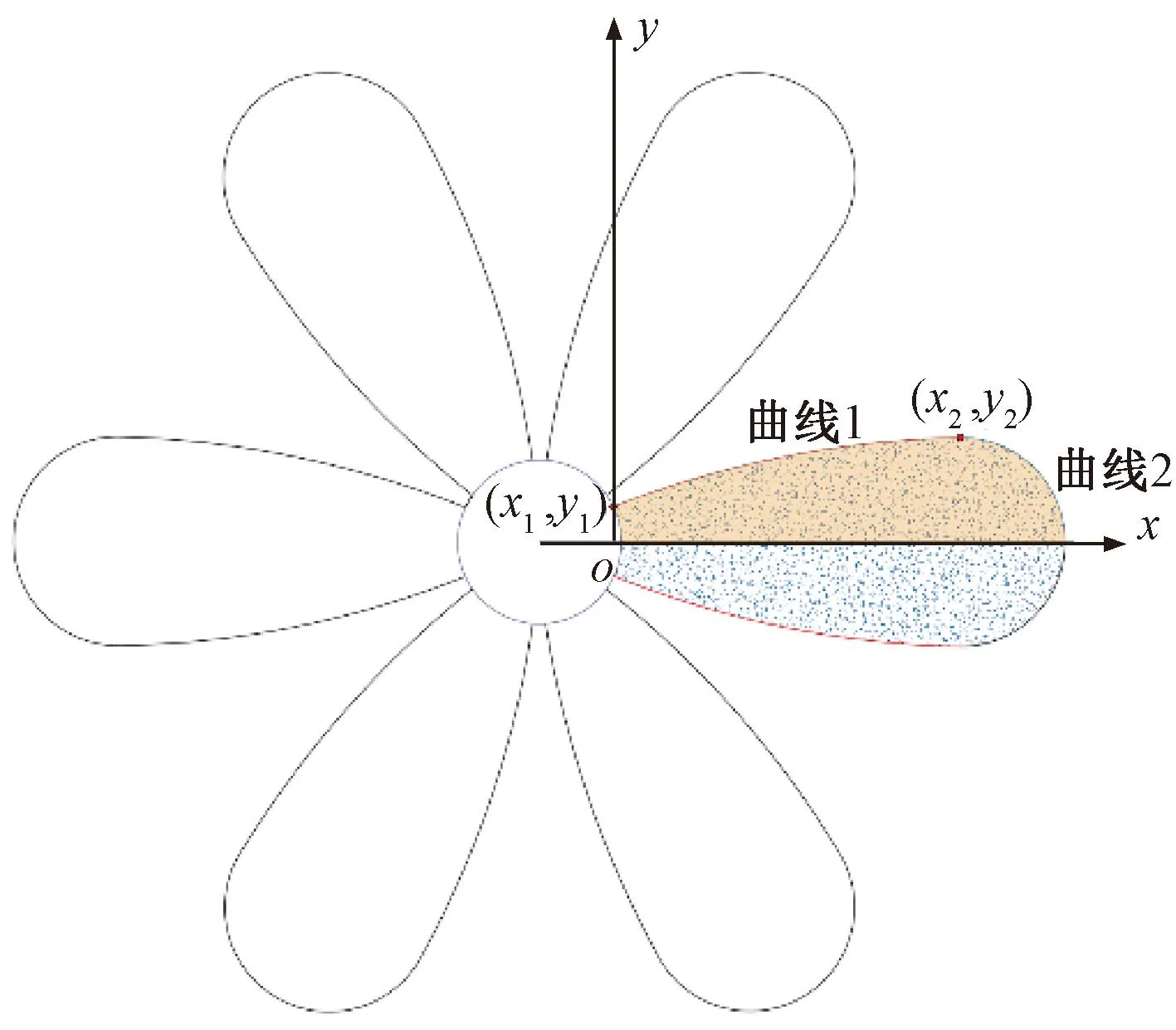
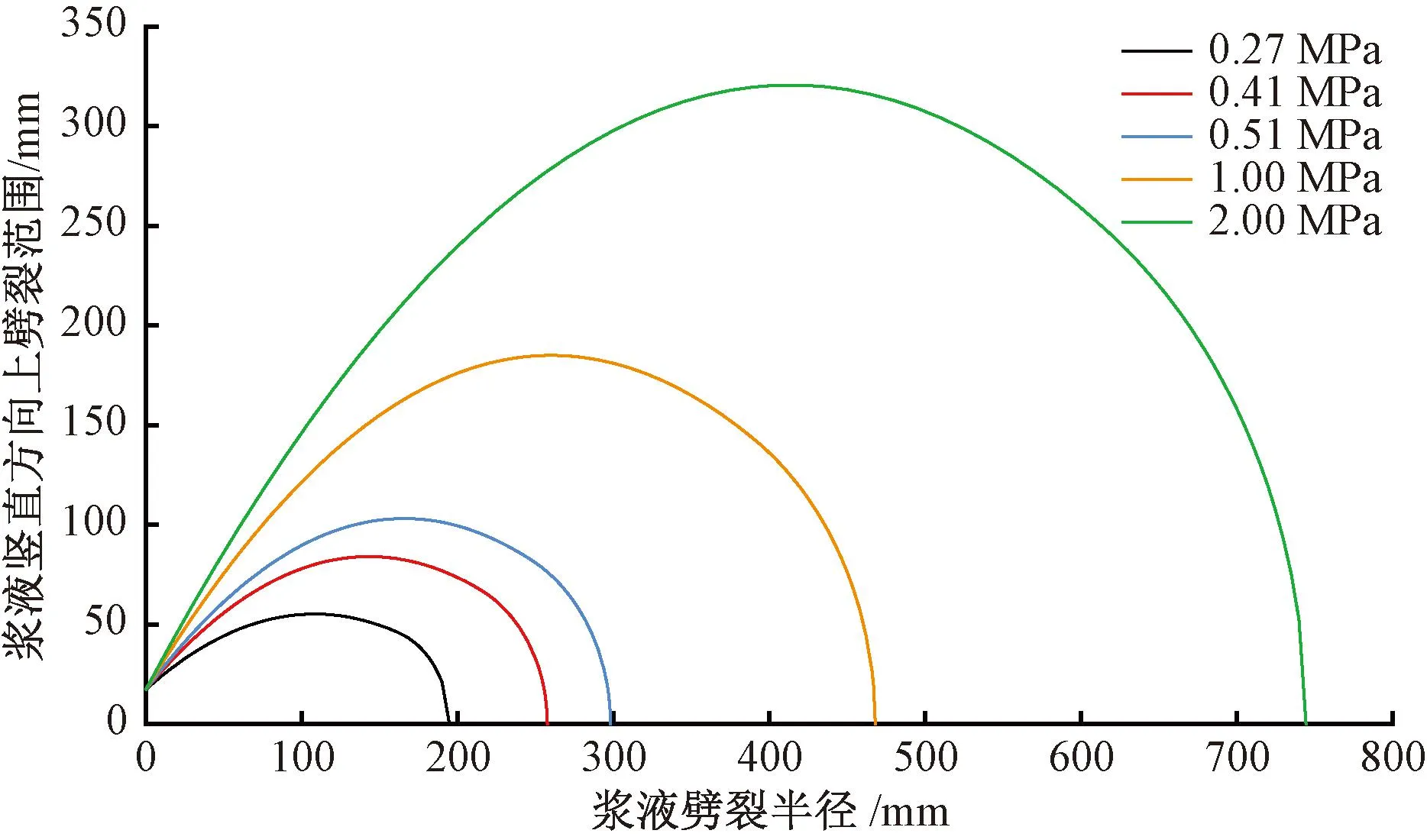
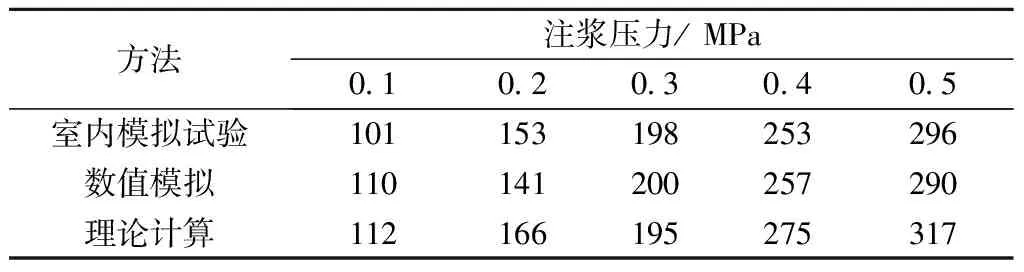
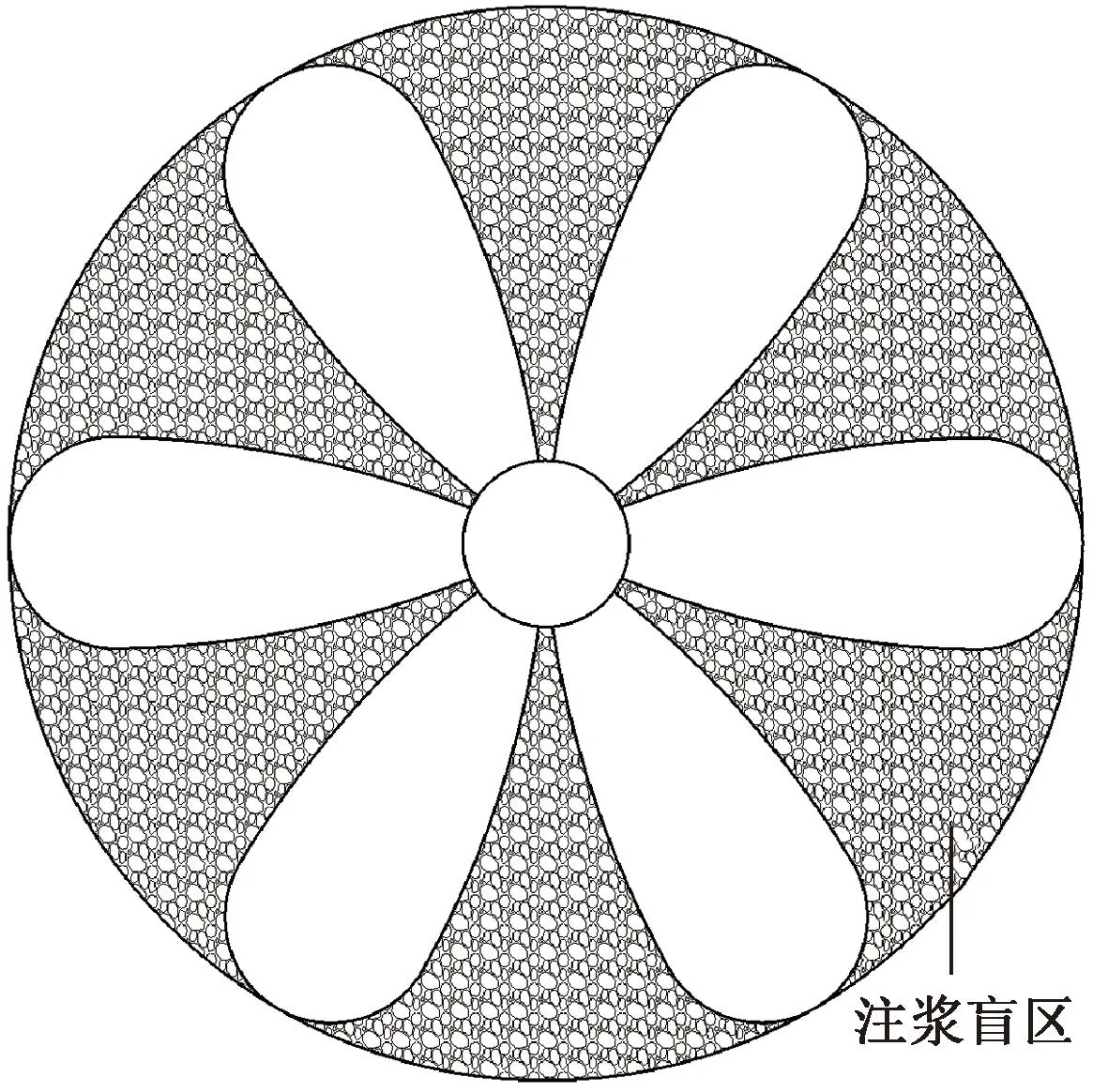
本文选取现场典型黄土土样,参照GB/T 50123—2019《土工试验方法标准》[17],测得试样含水率为12.28%,土样级配曲线见图1。试样颗粒级配主要集中在1~10 mm,计算得到Cu=5.78>5,1 图1 颗粒级配曲线 本文采用的注浆试验系统主要包括模型箱体和注浆机。模型箱体主要包括加固肋、土体介质、有机玻璃板。为防止注浆过程中发生堵管,选择高压橡胶管来输送浆液。箱体为正方体,边长为1.2 m,体积约为1.73 m3,主要材质为有机玻璃板及角钢。箱体顶部预留直径60 mm的圆孔,用于插入注浆管。考虑到注浆过程中产生的振动可能会导致注浆管倾斜,需对注浆管进行固定。 注浆管采用钢花管,外径为6 cm,内径为5.4 cm,全长为130 cm。在距注浆管底部10 cm处设置4排注浆孔,每1排距离为10 cm,每排设置6个直径为1.6 cm的注浆孔。钢花管设计见图2。 图2 注浆管设计(单位:cm) 本试验采用成都杰瑞达公司生产的型号为JRD200螺旋泵注浆机,外形尺寸为1.9 m×0.58 m×0.785 m(长×宽×高),料斗容积为130 L。注浆压力为0~3 MPa,其输送距离在水平方向可达180 m以上,在垂直方向可达60 m,出浆量可达1 500~2 500 L/h,压力、流速均可调。 模型采用逐层填筑、人工夯实的方法进行制作,模型至少填筑2/3。填筑过程中通过换刀法测试干密度,以此控制压实度,保证填筑土样的均匀性。在模型填筑过程中,预先将注浆管放置于模型箱中央。模型填筑完成后,在箱体顶部设置螺栓及管套用于加固注浆管。注浆试验装置见图3。 图3 注浆试验装置 模型箱填筑完成后,使用输浆管连接注浆机与模型箱。输浆管、模型箱、注浆机采用内螺纹进行连接,保证紧密性,防止产生漏浆和堵浆。 考虑到模型箱的尺寸,本次注浆试验的每次注浆量都采用相同体积的流量,即总流量均为0.1 m3。本次试验使用1排共计6个孔进行注浆,即对单排孔浆液的扩散范围进行研究。本试验选择0.1、0.2、0.3、0.4、0.5 MPa共5个注浆压力作为加载工况。 2.4.1 扩散半径 在浆液凝固之后,将注浆加固体挖出,发现随着注浆压力的增加,浆液的扩散范围逐渐增大,劈裂效果越明显。对不同注浆压力下加固体的浆脉长度进行测量。不同注浆压力下注浆体的扩散范围数据见表1,加固体长度统计曲线见图4。 表1 单排孔注浆加固体测量数据 图4 加固体浆脉长度 由图4可知,随着注浆压力的增大,浆液的扩散范围逐渐扩大,加固体长度与注浆压力的关系近似呈幂指数形式。不同的注浆压力下浆液扩散宽度差别不大,加固体宽度范围为5.5~8.4 cm。0.5 MPa下的浆液扩散宽度为8.4 cm,可能是由于注浆压力过大造成的。 2.4.2 注浆前后强度对比 参照文献[17],对黄土试样及注浆体进行直剪试验。直剪试验选取的注浆体为黄土和水泥浆液相互渗透形成的混合物。 不同垂直应力下未注浆试样以及浆液混合物的剪切位移-剪切力关系曲线见图5。由图5可知,在不同垂直应力下,混合物的强度显著提高。由上述所得未注浆土体和注浆混合体τmax-σ关系曲线见图6。由图6可知,计算得到未注浆土体的内聚力为41.65 kPa,内摩擦角为26°,黄土-浆液混合物的内聚力为71.8 kPa,内摩擦角为27.7°。前述分析表明水泥浆液经过渗透、挤压与土体相互耦合作用形成的混合土物,相比于未注浆土体强度有着显著的提升。 图5 未加固、加固土体剪切位移-剪切力关系曲线 图6 未注浆土体和混合土样τmax-σ关系曲线 目前针对高铁无砟轨道路基注浆数值仿真分析软件主要使用Ansys和PFC2D,但两者在模拟流体时存在局限性。为充分考虑流体和土颗粒之间的相互作用,本文选用有限元软件Fluent与离散元软件Edem进行耦合计算。在耦合计算中,Fluent用于模拟分析注浆液体的流动,Edem用于模拟分析土体颗粒在浆液作用下的运动。Edem-Fluent耦合能够全面准确地模拟颗粒与流体之间的相互作用,能够考虑流体对颗粒的作用力以及颗粒对流体的阻力。 本文采用的Edem-Fluent耦合计算方法主要包括以下4步:①在Fluent中收集Edem中颗粒的相关信息,包括速度、位置、数量等;②在Fluent进行流场计算直至收敛;③将Fluent计算得到数据传输至Edem中,进行动力学计算;④Edem中颗粒会产生新的位置、速度等基本量,以动量形式导入Fluent中,计算至收敛。将上述4个步骤循环一次为一个时步。耦合模拟流程见图7。 图7 耦合模拟流程 模型尺寸为60 cm×60 cm×10 cm(长×宽×高)。注浆管半径为4 cm。在注浆管距箱底4 cm处,对称开6个注浆孔,注浆孔半径为1 cm。模型四周为墙体,防止颗粒“逃出”。颗粒与墙体的力学参数选用默认值,并在其中填入等半径为2 mm的黄土颗粒,共填入615 273个颗粒。模拟0.12、0.17、0.22、0.27、0.41、0.51 MPa共6个注浆压力作用下接触力链的破坏。模型中每隔5 cm设置一个监测圆,共记5个,从内到外编号依次为1~5,选用Hertz-Mindlin黏结模型对土体进行模拟。参照文献[18-19],黄土试样力学参数见表2。 表2 黄土试样力学参数 参照文献[18,20-22],模型微观力学参数见表3。本文采用0.6∶1的纯水泥浆液对其进行数值模拟分析,在Fluent中设置其浆液密度为1 760 kg/m3,结合资料和水泥浆液材料,动力黏度取值0.06 kg/(m·s),颗粒间静摩擦系数为0.53。 表3 黄土试样微观力学参数 0.51 MPa注浆压力下,模型整体接触力链破裂图以及注浆孔平面土体接触力链的破坏见图8。将黄土的注浆孔平面接触力链的破坏图导入到相应的软件中,绘制包络图,统计得到不同注浆压力的注浆体扩散范围数据,将模型试验得到的扩散范围和数值仿真结果进行对比,结果见图9。由图9可知,两者差别较小,且增长趋势与幂指数相似。 图8 0.51 MPa下接触力链破坏 图9 模型试验与数值仿真对比 前述黄土数值模拟计算模型,共建立了5个监测圆柱,对其力链数据进行输出并进行统计,绘制每个监测圆中所断裂的力链数比重,见图10。由图10可知,注浆压力为0.12 MPa时,变化幅度最小,注浆压力为0.51 MPa时,变化最大。表明注浆压力越大,土体间的微观作用力作用更加分散,在浆液劈裂方向上,注浆压力是呈消散分布的,注浆压力越大,注浆压力消散速度越慢,从宏观层面上来讲,表现为浆液劈裂长度的变化。 图10 接触力链分析 根据试验现象以及数值仿真结果,浆液扩散范围曲线见图11。将浆液扩散范围曲线分段进行离散化,可得到不同段曲线的坐标。参照郭晋豪[23]的研究,将一个注浆孔注浆浆液扩散范围的上半部分曲线分为:曲线1、曲线2。曲线1为对数曲线,曲线2为圆曲线的一部分。分别对两段曲线进行拟合,可得到浆液扩散范围的曲线方程。计算所需坐标由试验及数值仿真得到。 图11 浆液扩散范围曲线 最终得到的曲线方程为 ( 1 ) 式中:x1、y1分别为注浆管、射浆孔半径;x2、y2为两曲线连接处的坐标;p为注浆压力,MPa;R为土体微观层面接触力链破坏范围半径。 通过计算可得到0.27、0.41、0.51、1.00、2.00 MPa注浆压力下扩散范围曲线,见图12。由图12可知,0.27 ~0.51 MPa注浆压力下浆液扩散范围与数值分析一致,在此基础上对1.00、2.00 MPa的注浆压力进行预测。 图12 软土体浆液扩散区域验证与预测 将理论计算、数值模拟、室内模型试验得出的黄土注浆浆液扩散半径进行统计,见表4。3种不同方法得到的浆液扩散范围的数据相差不大,扩散半径的变化规律一致,验证了理论计算与数值仿真的正确性。 表4 3种方法得到的浆液扩散半径验证 mm 前述给出了黄土注浆浆液扩散范围计算公式,但在浆液的扩散过程中存在盲区,由于钢花管开孔等原因,这部分土体浆液未能扩散过去,因此需要对扩散盲区边界进行推导。在扩散范围之外为注浆盲区,其示意见图13。 图13 注浆盲区示意 为简化推导过程,取两个叶片作为研究对象,见图14。首先推导曲线3。通过计算得出上、下部曲线的对称轴与x轴夹角为30°,注浆孔圆心坐标为(-35.5,0),扩散半径为R,对称轴方程、外围扩散半径圆的方程分别为 图14 局部注浆盲区范围 ( 2 ) (x+35.5)2+y2=R2 ( 3 ) 取对称轴上一点(0,20.5),此点为上、下部曲线中心对称点,令 ( 4 ) 则式( 4 )关于对称轴对称的方程为 ( 5 ) a、b为曲线中心对称点,令a=0,b=20.5,得到上部曲线3的表达式,即 ( 6 ) 由此,上部圆曲线4部分的表达式为 ( 7 ) 结合式( 6 )、式( 7 )得到上部整体曲线的表达式。式( 1 )、式( 6 )、式( 7 )相结合即为注浆扩散盲区的边界表达式。 本文以大西高铁沿线典型湿陷性黄土路基为研究对象,设计完成了黄土注浆模型试验,使用Edem-Fluent耦合技术进行注浆数值仿真,对注浆参数进行研究,得出以下结论: 1)模型试验结果表明,随着注浆压力的增大,浆液的扩散范围逐渐扩大,加固体长度与注浆压力的关系近似幂指数。注浆后土体强度明显提升。 2)数值仿真结果表明,浆液在土体中扩散的本质是注浆压力在土体中的消散过程。注浆压力较大时,压力在土体介质中消散得慢,宏观表现为扩散半径较大。 3)通过理论推导得出了黄土注浆扩散范围与注浆压力之间的计算式,符合模型试验与数值仿真结果,在此基础上得出了注浆压力与注浆盲区理论表达式。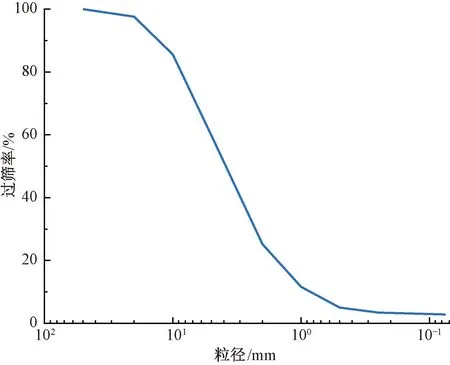
2.2 注浆试验装置
2.3 试验步骤

2.4 注浆试验结果分析
3 数值仿真
3.1 Edem-Fluent耦合简介


3.2 数值仿真结果分析

4 注浆扩散及盲区推导
4.1 注浆扩散理论
4.2 注浆扩散盲区推导

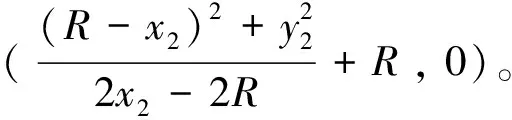
5 结论
——结构相互作用的影响分析

