退化系统的质量控制、状态维修与备件订购联合策略优化
韩梦莹, 马书刚, 杨建华, 李 伟, 马志超
(1. 河北经贸大学 商学院,石家庄 050061; 2. 北京科技大学 经济管理学院, 北京 100083; 3. 北京企业低碳运营战略研究基地,北京 100083; 4. 河北工程大学 管理工程与商学院,河北 邯郸 056038)
基于状态的维修策略可以根据状态检测或监测收集到的信息建议维修活动,常被应用于实践中[1].维修活动导致备件需求,备件是维修活动能够顺利执行的重要保障,二者相互影响与制约.对于关键生产系统(单部件系统)而言,系统的功能退化不仅是引发维修需求的根源,而且是导致产品质量下降的最主要原因[2].因此,根据关键生产系统的功能退化过程,确定质量控制、状态维修及与之匹配的备件订购策略,对于提升产品质量、提高设备可靠性、降低运营成本有积极意义.
延迟时间模型(Delay-Time Model, DTM)由于能够建立系统状态与维修活动之间的关系,已被广泛应用于离散劣化系统的状态维修策略模型中[3-4].如,刘勤明等[5]建立了基于周期检测的单位时间费用模型,优化检测周期和预防性维修阈值;Yang等[6]将基于状态的不完美维修策略与基于时间的预防更换策略相结合,优化检测周期、检测次数和预防性更换周期;Zhang等[7]则构建了优化两阶段检测周期和次数的预防性维修模型.将设备维修与备件管理策略进行联合优化,确保维修时刻备件的可得率已被国内外许多学者提出并研究[8-10],近年来,利用DTM对状态维修与备件订购策略进行联合优化的研究也逐渐增多.如,赵斐等[11]与韩梦莹等[12]构建了基于时间的备件订购与状态维修联合策略模型;Zhao等[13-14]则提出了基于系统状态的备件订购策略,建立了非周期检测与备件订购联合策略优化模型.
对生产企业而言,质量控制和设备维护这两项运营策略必须相互协作以确保生产过程的产出率[15].上述研究虽然为设备维护以及设备维护与备件订购联合策略优化分析提供了基本框架,但并未考虑系统劣化对产品质量的影响.鉴于此,Wu等[16]利用统计过程控制图监控产品质量,以确定最优的检测策略;Azimpoor等[2]以产品质量评估系统状态,认为次品率为某一固定常数时,系统处于正常状态,而当次品率超出该固定值时,说明系统已进入缺陷状态,应立即进行预防性更换,据此优化检测周期和产品质量;Han等[17]基于DTM构建了考虑缺陷品损失的状态维修与备件订购联合策略优化模型,但并未考虑产品质量的控制问题.
综上,现有基于DTM的质量控制、设备维护和备件订购联合决策研究,在理论与实际应用层面尚存在以下3个方面的局限性:① 产品质量、系统维修与备件管理3个要素之间存在密切联系,但鲜有文献同时考虑质量控制、状态维修与备件订购,对三者进行整合研究;② 在系统状态与产品质量相关时,一旦次品率超出前期固定水平就进行预防性更换[2],易导致过度维修;③ 备件订购提前期假定为固定常数,实际上由于受多种因素的影响,备件订购之后的交付期具有随机性特征[18].针对这些不足,本文将状态检测信息和质量检验信息作为互补,进行预防性维修决策,针对退化过程服从延迟时间理论的关键生产系统,提出质量控制、状态维修与备件订购联合策略.
1 问题描述与模型符号
1.1 问题描述
(1) 系统退化过程及系统状态与次品率关系说明.
系统退化过程服从延迟时间理论,即系统由初始新状态退化到故障状态要经历正常阶段和缺陷阶段,其中X和Y分别表示正常阶段和缺陷阶段持续时间的随机变量,如图1所示.系统的状态空间也因此被划分为:正常、缺陷和故障.系统退化的两个阶段由Weibull分布来描述[11-15],Weibull分布的故障率函数为h(t)=απ(αt)π-1(α>0,π>0,t≥0),其中α为尺度参数,π为形状参数,t为时间随机变量.
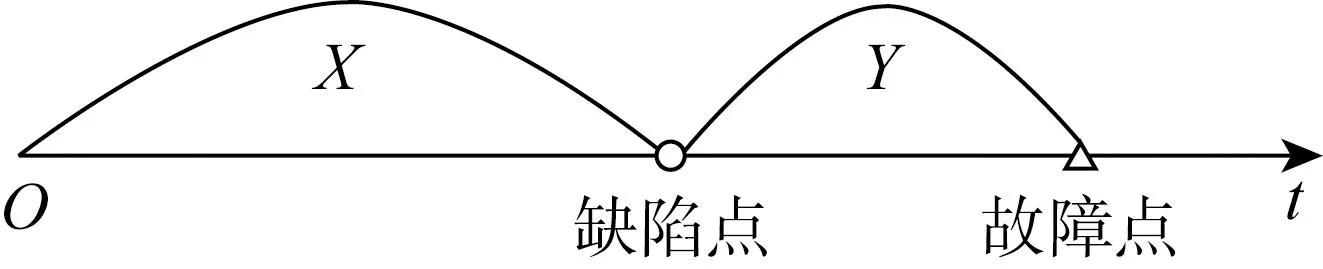
图1 延迟时间理论Fig.1 Concept of delay time
系统的运行状态与产品的加工质量密切相关.系统处于正常状态时,次品率固定在β1水平;一旦系统进入缺陷状态,次品率则是关于缺陷状态实际持续时间,即缺陷点到达时刻与系统更换(预防更换或故障更换)需求发生时刻之间的时间间隔t1的单调递增函数,可用β2(t1)表示,其公式如下:
(1)
式中:β1为系统刚进入缺陷状态时的次品率;λ为产品质量退化的边界值;κ和ε为正常数.
(2) 两阶段检测的质量控制及状态维修策略说明.
①在系统退化初期以周期T(决策变量)检查系统状态,而在退化后期以周期T检查产品质量,退化初期的检测视为第一阶段检测,退化后期的检测视为第二阶段检测.系统退化的前后期以检测初次识别系统缺陷的时间点为基准进行划分,并在该时间点进行质量检测.
②对产品采用100%的质量检测方法,一旦质检结果表明产品次品率超出阈值RP(决策变量),则需对系统进行预防性更换,该活动记为基于质量的更新;若第M(M≥1,为决策变量)次进行质量检测,次品率仍未超出阈值RP,为减少系统的故障发生率,需在第M+1次执行质量检测活动的时刻进行预防性更换(但该时刻不进行质量检测),记为基于状态的更新;若在检测期内系统突发故障,则需进行故障后更换,记为基于故障的更新.
③无论是状态检测还是质量检测,检测结果都是完全可靠的.
(3) 质量控制、状态维修及备件订购联合策略优化.
在检测第1次识别系统缺陷状态时,进行备件订购,备件订购时刻与备件交付时刻之间的时间间隔随机,随机订购提前期LR服从参数为ν和σ的正态分布,即LR~N(ν,σ).由上文描述可知,系统存在3种更新方式:基于质量的更新、基于状态的更新和基于故障的更新.系统预防性更换或故障更换需求发生时,需要考虑备件的可得性:若备件已入库,则立即更新系统;若备件订购已下达但未交付,需等待备件进行交付;若备件未订购则立即订货,并在备件到达后更新系统.
1.2 模型符号
对模型构建过程中涉及的其他符号进行说明,如表1所示.

表1 主要模型符号及说明Tab.1 Main notations and illustration for the model
2 模型建立
将系统寿命周期内的第n个检测期定义为从第n-1次检测结束时刻到第n次检测结束时刻之间的时间间隔,若在检测期内需对系统进行更换,则此时的检测期定义为从上一次检测结束时刻到系统更换完成时刻之间的时间间隔.令CT,n表示第n个检测期产生的总费用,LT,n表示第n个检测期期长.由系统退化过程的随机性、预防性更换和故障更换策略的描述可知,第n个检测期可能发生的事件如下.
事件1第n次检测时,识别系统处于正常状态,无需进行维修活动.
事件2第n次检测时,初次识别系统缺陷状态,且次品率未超出阈值RP,无需进行维修活动.
事件3第n次检测时,非初次识别系统缺陷状态,次品率未超出阈值RP且质量检测次数未超出阈值M,无需进行维修活动.
事件4第n次检测时,质量检测次数未超出阈值M,但次品率超出阈值RP,需进行基于质量的更新.
事件5第n次检测时刻,质量检测次数超出阈值M,需进行基于状态的更新.
事件6系统在第n个检测期内突发故障,需进行基于故障的更新.
2.1 第n次检测时,识别系统处于正常状态,无需 进行维修活动

(2)

2.2 第n次检测时,初次识别系统缺陷状态,无需 进行维修活动

(3)
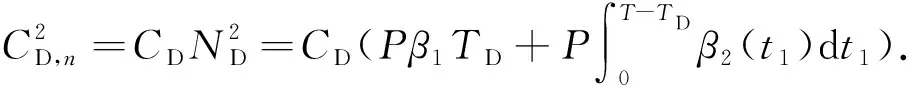
2.3 第n次检测时,非初次识别系统缺陷状态,无 需进行维修活动

(4)

2.4 第n次检测需进行基于质量的更新


(5)
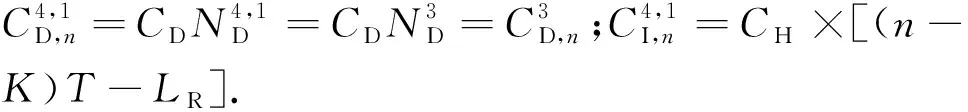

(6)


(7)

2.5 第n次检测时刻需进行基于状态的更新
因该事件下备件已进行订购,则必然存在M≥1,同时存在2种更新场景.

(8)


(9)

2.6 系统在第 n 个检测期内突发故障, 需进行基 于故障的更新
令TF为第n-1次检测结束至系统故障点的时间段,该事件下,有n-K≤M成立.考虑系统故障时备件的状态,存在3种更新场景.
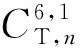
(10)


(11)
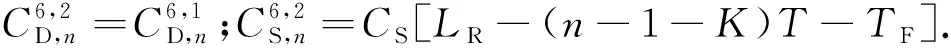

(12)

2.7 联合策略优化模型
由上述分析可得,第n个检测期产生的总成本为
(13)
式中:χ(k)为示性函数,若事件k发生则值为1,否则值为0;χ(k,j)也为示性函数,若事件k下的场景j发生则值为1,否则值为0.
同样可得,第n个检测期的期长为
(14)
若N为[0,Γ]时间段内总的检测期数,则该时间段内的平均费用率C(T,M,RP)可表示为

(15)
该联合策略模型可概括为以下非线性、混合整数、随机优化问题:
minC(T,M,RP)
(16)
s.t.β1≤RP<1
T,M∈N*
3 对比模型及优化算法
3.1 对比模型

(17)
s.t.β1≤RP<1
T∈N*
3.2 离散事件仿真算法
因模型1和2的目标函数中存在大量不确定性因素,如系统状态、备件状态及[0,Γ]时间段内的检测期总数等,故通过离散事件仿真算法模拟系统的更新过程,实现对式(16)~(17)的近似求解.模型1的离散事件仿真算法流程图如图2所示,主要步骤如下.
步骤1设置模型初始参数,包括时间阈值Γ、P、CIC、CIQ、CR、CP、CF、CS、CD、CH、系统两阶段故障率退化参数和次品率参数.
步骤2设置决策变量T、M和RP.
步骤3设置[0,Γ]时间段内的总费用CT=0,总的时间长度LT=0.
步骤4设置更新周期内的当前检测期数n=0,更新周期内的当前检测时刻TT=0.
步骤5根据相关分布及参数生成随机持续时间X和Y及LR.并令x表示缺陷点,y表示故障点,有x=X和y=x+Y成立.
步骤6若LT<Γ,系统更新周期内的检测期数n=n+1和检测时刻TT=TT+T逐渐累加;否则,输出目标函数值C(T,M,RP).
步骤7若当前检测时刻小于缺陷点到达时刻,则表明系统在检测时刻处于正常状态.因此,若TT 步骤8若当前检测时刻TT≥y则表明系统在第n个检测期内发生故障,且故障时刻并未订购备件,即事件6中的场景3发生,在求得TD和TF的基础上,计算CT和LT,并返回步骤4.反之,若TT≥y不成立则意味着TT时刻检测时初次识别系统的缺陷状态,此时有K=n成立并可求得TD,转到步骤9. 步骤10若LT<Γ,则系统更新周期内的检测期数按n=n+1逐渐累加,而检测时刻按TT=TT+T逐渐累加,并转到步骤11;否则,输出目标函数值C(T,M,RP). 步骤11若TT≥y,首先应计算TF,然后进一步判断故障时刻备件所处的状态.此时若LR≤y-KT,则备件已入库,事件6中的场景1发生,计算CT和LT,并返回步骤4;若LR>y-KT,则备件已订购但未交付,事件6中的场景2发生,计算CT和LT,并返回步骤4.若TT 步骤12通过n-K 步骤14若LR≤(n-K)T,则表明质量更新需求时刻备件已入库,事件4中的场景1发生,计算CT和LT,并返回步骤4;否则,说明质量更新需求时刻备件已订购但未交付,事件4中的场景2发生,计算CT和LT,并返回步骤4. 值得注意的是,将图2中n-K 对于两个模型给定的决策变量(T,M,RP)和(T,RP),根据3.2节中离散事件仿真算法分别求得平均费用率数据.通过响应曲面法,利用Design Expert软件分别拟合模型1和2的二次平均费用率回归方程.拟合所得二次平均费用率函数连同约束条件构成非线性约束问题,进而借助MATLAB软件求解模型.多次重复以上过程,以获得全局近似最优解. 系统正常阶段和缺陷阶段故障率的退化参数分别为:α1=0.019,π1=1.5;α2=0.031,π2=1.5.模型次品率参数为:β1=0.005,λ=0.25,κ=0.008,ε=1.2.LR服从正态分布的参数为:ν=25,σ=3.其余参数设定为P=10 t/d,Γ=10 000 d,CIC=50元/次,CIQ=150元/次,CR=600元/次,CP=2 500 元/次,CF=4 300元/次,CS=250元/ (t·d-1),CD=80元/t,CH=15元/d. 采用三因素、三水平的Box-Behnken实验方案来拟合模型1的费用率函数C(T,M,RP).首先,利用离散仿真算法进行17组实验,每组实验重复200次,得出相应(T,M,RP)组合下的平均费用率.其次,借助Design Expert软件拟合二次费用率函数c(T,M,RP),得到的二次回归方程如下: (18) 图3 c(T, M, RP) 随T和M变化曲面Fig.3 Surface of c(T, M, RP) with variation of T and M 图4 c(T, M, RP) 随T和RP变化的曲面Fig.4 Surface of c(T, M, RP) with variation of T and RP 表2 模型1方差分析(ANOVA)相关结果Tab.2 Correlation results of ANOVA for Model 1 因模型2具有两个决策变量,故选用两因素、两水平的Central Composite实验方案进行13组实验,每组实验重复200次,以拟合模型2的费用率函数C(T,RP),得到的二次回归方程如下: (19) 图5 c(T, RP)随T和RP变化曲面Fig.5 Surface of c(T, RP) with variation of T and RP 表3 模型2方差分析(ANOVA)相关结果Tab.3 Correlation results of ANOVA for Model 2 将两个模型的最优结果进行比较,可知:模型1的最优结果小于模型2的最优结果.这说明与仅考虑质量控制的预防性维修和备件订购联合策略相比,同时考虑质量控制和系统状态的预防性维修与备件订购联合策略,能够有效降低系统的平均费用率. 由4.1节可知,影响模型最优解的参数有很多,此处以CF为例进行敏感性分析,这是因为与其他情况相比,设备故障后的维修费用更高,给企业带来的经济损失更大,选取其进行敏感性分析具有一定的代表性.表4给出了不同CF取值下,模型的最优结果. 表4 CF敏感性分析结果Tab.4 Sensitivity analysis results of CF 对关键生产系统的质量控制、状态维修与备件订购进行了联合建模与优化.利用两阶段延迟时间故障过程刻画系统的退化过程,并认为系统状态与产品质量相关:系统处于正常状态时,次品率保持不变;系统处于缺陷状态时,次品率是关于缺陷状态持续时间的单调递增函数.以检测初次识别系统缺陷的时间点为基准划分系统退化的前后期,设计了在系统退化初期检查系统状态,而在退化后期检查产品质量的两阶段检测策略.为了降低系统故障率、避免系统过度维修,提出将系统状态检测信息和产品质量检验信息同时作为预防性维修决策的依据.以检测周期、状态维修阈值和质量控制阈值为决策变量,建立了有限时域内的平均费用率模型,并设计离散仿真算法对模型快速近似求解.通过与传统的仅考虑质量控制的预防性维修与备件订购联合策略对比,实验分析结果表明,在既定参数下本文所提的质量控制、状态维修与备件订购联合策略能够有效降低运营成本.

3.3 目标函数的估计与优化
4 实验分析
4.1 参数设置
4.2 模型1结果分析



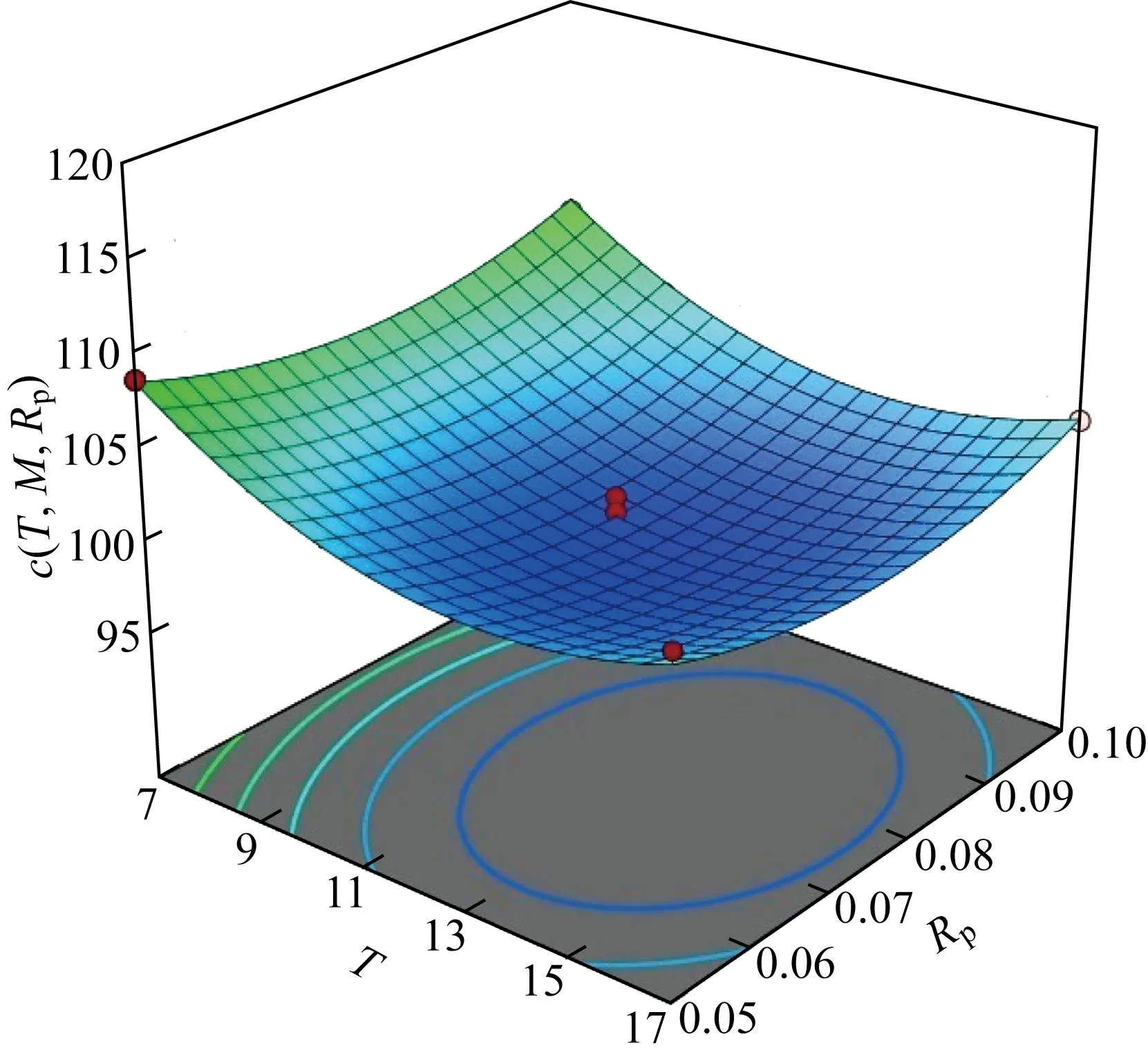
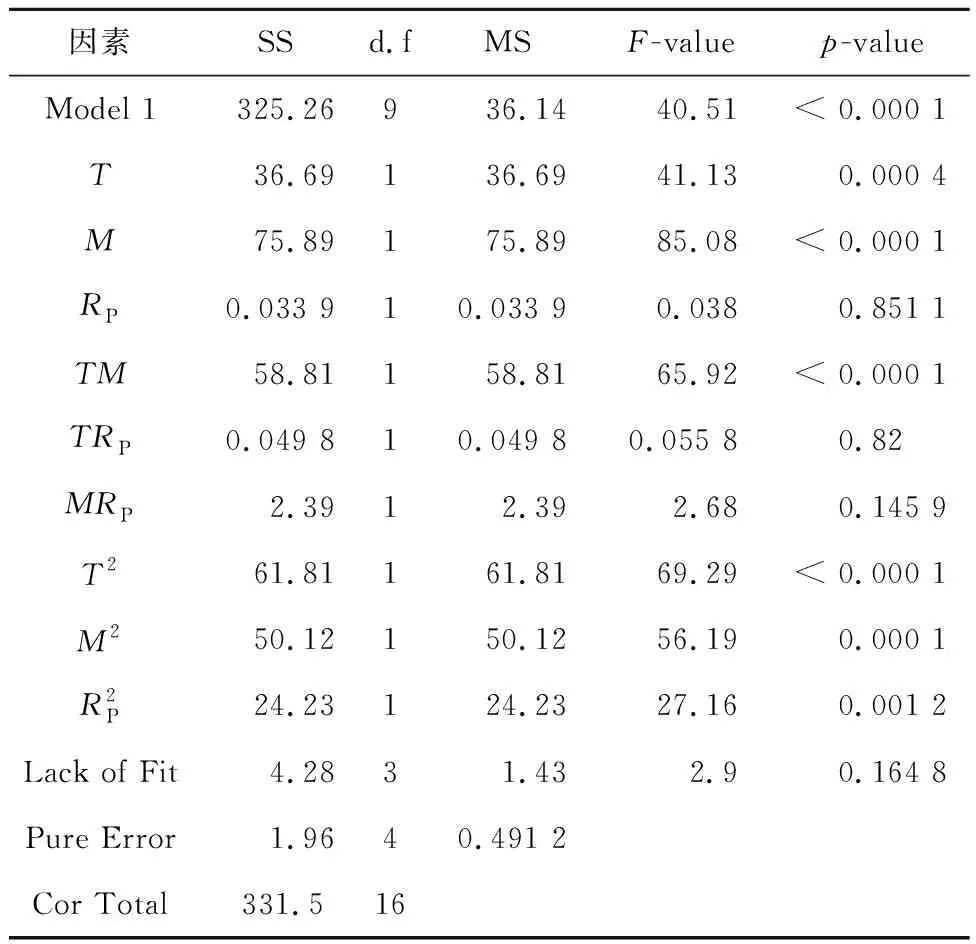
4.3 模型2结果分析




4.4 敏感性分析


5 结语

