基于代理模型估值不确定度的昂贵多目标优化问题研究
张晶 裴东兴 马瑾 沈大伟


摘要:针对代理模型辅助的多目标优化算法中个体不确定度之间相互冲突的问题,本文提出个体每个目标估值不确定的填充准则,同时,为了减少训练模型消耗的计算资源,提出基于非支配排序的样本选择算法。为了验证该算法的可行性,采用DTLZ和WFG测试函数进行测试,得出结果与近些年发表5种具有代表性的同类型算法进行对比,结果说明该算法可以有效的解决昂贵高维高目标优化问题。
关键词:进化算法;昂贵多目标优化问题;代理模型;填充准则;不确定度
中图分类号:TP391文献标志码:A文献标识码
A research for expensive many-objective optimization problem based on uncertainty of surrogate
ZHANG Jing1,PEI Dongxing2,3,MA Jin1,SHEN Dawei2,3*
(1 Department of Internet of Things Technology, Shanxi Vocational & Technical College of Finance & Trade,Taiyuan,
Shanxi 030031, China; 2 Science and Technology on Electric Test and Measurement Laboratory,North University of China,Taiyuan,
Shanxi 030051,China; 3 Key Laboratory of Instrumentation Science and Dynamic Measurement,Ministry of Education,North University
of China,Taiyuan,Shanxi 030051,China)
Abstract: In surrogate assisted many objective optimization, conflicting uncertainties of surrogate between objective is a challenge. Hence, an many objective optimization algorithm with uncertainty of surrogate is proposed called, US-MOEA. The main work of this paper is as follows: first of all, infill criterion based on the uncertainty of predicted value is proposed to select promising solutions for re-evaluating by expensive optimization objective function. Then, in order to reduce the computational resources, a method based on non-dominated sorting is used to select some individual as train sample. In order to verify the effectiveness of proposed algorithm, the DTLZ and WFG test suits problem are applied and compare with five the-state-of-art algorithms proposed in recent years. The experimental results illustrate that the US-MOEA is an effectively method for solving expensive many objective optimization problems.
Key words: evolutionary algorithm; expensive many objective optimization problem;surrogate;infill criterion;uncertainty
0 引 言
多目標优化问题(Multi-objective Optimization Problem, MOP)是一个常见的学术问题,在风能预测[1],车辆调度优化[2]等工程应用中尤为常见。相较于单目标优化问题,在多目标优化问题中包含多个相互冲突的目标函数,且在优化过程中需同时考虑所有的目标函数。这意味着单个解不能同时使所有目标函数达到最优[3],故在多目标优化问题中,往往求得的是一组折衷的解集。另外,在工程应用中,一些优化问题的单次评价成本很高或者需要较长的时间成本,称为昂贵多目标优化问题 (Expensive Many Objective Optimization Problem, EMOP)。当使用普通多目标优化算法[4-5]在求解多目标优化问题时,往往需要数以万计的评价次数。因此,当使用普通多目标优化算法求解昂贵多目标优化问题时,所需要的优化成本是难以令人承受的。一种有效的方法是先采用计算廉价的代理模型拟合昂贵的目标函数,然后采用普通的进化算法求解代理模型的最优解,随后依据填充准则选择合适的解用于真实计算,并将其保存到数据库来更新模型或输出最终种群,这类型优化算法称为代理模型辅助的进化算法(Surrogate-assisted evolution algorithm, SAEA)。
昂贵多目标优化问题由于在解决实际问题中具有广泛应用价值,因此受到众多学者的关注,近些年提出许多优秀的代理模型辅助的多目标优化算法,这些算法依据代理模型的使用方法大致分为两类[6],分别为通过代理模型预测个体的指标和依据代理模型拟合待优化问题的目标函数。在依据代理模型拟合目标函数的算法中,主要依据代理模型拟合个体的支配关系和切比雪夫函数值等,例如在算法ParEGO[7]中,数据库中的个体依据参考向量得到个体的切比雪夫值,随后针对切比雪夫值建立代理模型。在CPS-MOEA[8]中采用分类模型预测个体之间的支配关系,并且选择初步解进行真实计算。在CSEA[9]中,采用前馈神经网络作为分类器,预测候选解和参考点之间的支配关系。由于个体的切比雪夫值依据参考向量而得到,但是当解决不规则帕累托面的多目标优化问题时,参考向量往往随着种群的进化过程发生自适应变化,因此限制了ParEGO算法的应用。另外,由于基于支配的多目标优化算法在解决高维多目标优化问题时效果不理想,因此,采用代理模型预测个体间支配关系的算法并不多。大部分算法为采用代理模型拟合待优化问题的目标函数,例如在KRVEA[10]中,采用高斯过程模型拟合目标函数,在填充准则中依据个体的估值和不确定度选择合适的个体进行真实计算。在EDNARMOEA[11]中,采用Droupout网络拟合目标函数,并且提出依据个体的目标函估值和不确定度提出可以平衡种群多样性和收敛性的填充准则。在KTA2[6]中,采用由3个高斯过程构成的集成模型拟合目标函数,并且提出将种群状态分为多样性状态,收敛性状态和不确定度状态,随后依据个体的估值和不确定度提出相应的填充准则。
在多目标优化算法中,由于个体具有多个目标函数值和不确定度,并且传统的方法往往将多个不确定度的均值作为个体的不确定度,这种方法并不能很好的反映个体的每个目标的不确定度信息。针对该问题,本文提出估值不确定度的昂贵多目标优化算法(US-MOEA),具体如下:
(1)提出依据估值不确定度的填充准则,与传统的将个体的所有不确定度的均值作为选择依据不同,为了充分发挥个体不确定度,本文依据个体每个估值的不确定度选择个体进行真实计算。为了平衡种群的多样性和收敛性,在每个目标上随机选择估值最大或者最小的个体进行真实计算。另外,在单次优化中,选择较多的个体进行真实计算会导致计算资源的浪费,因此在解决昂贵高维多目标优化问题时,随机选择其中的一半目标函数,并且基于这些目标函数选择个体。
(2)由于高斯过程模型在给出个体估值的同时提供估值的不确定度,因此在基于代理模型辅助的优化算法中广泛应用。然而,随着训练样本数量的增多,训练模型所需要的时间会急剧增加。针对该问题本文提出基于非支配排序的训练样本选择方法。
1 资料与方法
基于代理模型辅助的多目标优化算法是解决昂贵高维多目标优化问题的有效方法,其中,填充准则在基于代理模型辅助的优化算法中起着十分重要的作用[10]。在填充准则中,个体的不确定度是选择恰当的个体进行真实计算的重要依据。具体为,当选择不确定度小的个体进行真实计算,有助于增加种群的收敛性;当选择不确定度大的个体进行真实计算,则有利于改善种群的多样性,并且经过真实计算的个体往往会保存到数据库中作为新的训练样本更新模型,因此,该类型个体也有助于增加模型的精度[12]。然而,在昂贵高维多目标优化问题中,个体的所有目标函数都通过模型估值获得,因此,该个体具有多个不确定度值。在传统的代理模型辅助的多目标优化算法中往往通过个体多个不确定度的均值代表该个体的不确定度,但是均值并不能准确的表示该个体的不确定度信息。图1给出了3个个体P1,P2和P3分别在3个目标M1,M2和M3的不确定度值,图2展示了3个个体不确定度的均值。从图2中可得,个体P2和P3将会被选择进行真实计算。然而,从图1中发现,在M1目标上个体P3和P1将会被选择进行真实计算,在M2目标上P1和P3将会被选择,在M3目标上P1和P2将会被选择。综上可以看出,传统的基于不确定度均值的填充准则往往不能选择出恰当的个体进行真实计算,因此本文提出基于单个模型不确定度的昂贵高维多目标优化算法。
1.1 算法框架
在昂贵多目标优化问题中,由于待优化问题评 价成本昂贵,而传统的多目标优化算法在寻优时需要数以万计的评价次数,因此并不适合于解决该类型优化问题。
基于代理模型辅助的多目标优化算法是解决该类型优化问题的有效手段。在该类型优化算法中,常用的代理模型有径向基函数(Radial basis function, RBF),高斯过程(Gaussian processes, GP),支持向量机(Support vector machines, SVM),多项式回归(Polynomial regression, PR)等模型拟合目标函数。其中,GP模型在预测时可以同时给出个体的估值以及估值的不确定度,同时在填充准则中,合理的利用估值的不确定度可以选择出优秀的个体进行真实评价,因此GP模型被广泛应用。
US-MOEA算法流程如图3所示,首先依据历史数据建立代理模型用于拟合昂贵目标函;然后,建立的代理模型辅助算法寻优;最后,通过填充准则策略从优化后的种群中选择合适的个体进行真实评价。当满足终止条件时,输出数据库中的非支配解,否则,依据数据库中的样本更新模型。
1.2 选择训练样本训练代理模型
在GP模型中,随着训练样本数量的增加,模型的计算复杂度会急剧增加,因此本文提出基于非支配排序的训练样本选择方法,具体步骤如下:
步骤1:将数据库中的个体依据目标函数进行非支配排序得到F1,F2,…Fl;
步骤2:从第F1层开始,逐层选择个体直到Fj层(当选择F1~Fj层的所有个体作为训练样本时,样本數量超过NT (NT表示样本数量));
步骤3:从Fj层中随机选择NT-|F1~Fj-1|个样本,其中|F1~Fj-1|表示F1~Fj-1层所有个体的数量;
步骤4:依据选择出的样本为每个目标函数建立GP模型。
1.3 填充准则
在基于代理模型辅助的优化算法中,通过填充准则选择出个体进行真实计算后添加到数据库中,并且模型训练样本和种群寻优的初始父代种群均从数据库中选择,因此填充准则在基于代理模型辅助的优化算法中有十分重要的作用。另外由于GP模型在提供个体估值的同时可以提供估值的不确定度,所以,在US-MOEA中采用了GP模型拟合目标函数。
在进化算法中,平衡种群的多样性和收敛性是十分重要的,具体的讲,良好的多样性可以使得种群跳出局部最优,而寻找到全局最优;优秀的收敛性促使种群快速的寻找到全局最优解。因此,在填充准则中选择不确定度小的个体可以改善种群的收敛性,选择不确定度大的个体有利于增强算法的多样性。此外,由于模型的训练样本均从数据库中选择,因此,良好的数据库样本有助于建立优秀的代理模型。综上,在填充准则中同时选择不确定度最大和不确定度最小的个体进行真实计算是合理的,但是,在一次优化中选择较多的个体进行真实计算会消耗较多的评价次数,不利于算法解决昂贵高维多目标优化问题。
在昂贵多目标优化问题中,由于个体的所有目标函数都是通过模型预测得到,因此该个体具有多个不确定度值,这些不确定度值往往相互冲突。针对该问题,本文提出基于单目标不确定度的昂贵高维多目标进化算法。该算法的填充选择策略为依据个体在每个目标上不确定度的表现选择出恰当的个体进行真实计算。例如,图4展示了3个个体在m个目标上不确定度值,在M1目标上,个体P1和P3在该目标上的不确定度分别为种群中的最大值和最小值,同时,如上所述,在填充准则中一次选择较多的个体进行真实计算不利于算法解决昂贵多目标优化问题,因此P1或P3个体将会被选择;同理在M2目标上,P1或P3将会被选择,在M3目标上个体P1或P2将会被选择,以此类推。当所有的个体被选择出来时,删除其中的重复的个体后,进行真实计算。另外,当待优化目标数较多时,为了避免一次选择较多的个体,本文提出随机选择待优化目标函数中的一半目标函数,并且依据这些目标函数选择个体进行真实计算。
2 结果与分析
为了验证US-MOEA算法的性能,采用广泛用于验证昂贵多目标优化算法性能的DTLZ[13]测试函数和WFG测试函数,并且和近些年提出的优秀的同类型优化算法进行对比。本节首先介绍实验参数设置情况,然后通过消融实验说明该策略的合理性,最后详细展示了算法US-MOEA在2组测试函数的性能体现并且和同类型的优秀的算法进行对比。
2.1 实验参数设置
本文实验参数设置如下:种群数量NP为100,种群迭代次数ω为100,种群寻优过程中通过遗传算法产生子代,其中交叉概率为1,交叉因子为20,变异概率为1/D,其中D表示决策空间维度,变异因子为20。测试函数的参数设置如表1所示,同时为了实验的可信度,每个测试问题独立运行20次,取中位数进行比较,并且采用置信度σ为0.05的Wilcoxon秩和检验方法用于检验本文算法和对比算法结果之间有无显著性差异,其中“+”,“-”和“≈”分别表示本文所提算法相较于对比算法结果好、差和没有显著性差异。在DTLZ测试函数中采用IGD值评价优化结果的优劣,在WFG中采用HV指标来评价算法的优化结果。
2.2 算法性能度量指标
在DTLZ测试函数中,采用翻转世代距离(Inverted Generational Distance, IGD)来评价算法优化结果的优劣。公式(1)给出了IGD指标的计算方法,其中S表示经过算法的优化结果,F*表示多目标优化的最优解集,dist(x,S)表示最有解集中点x到集合S的最小距离。IGD值越小则表示算法的优化结果越好。
IGD(S,F*)=∑x∈F*dist(x,S)|F*|。(1)
在WFG测试函数中,采用超体积(Hypervolume, HV)来度量算法优化结果的优劣。公式(2)展示了HV的计算方法,其中,δ表示用来计算体积的测度,S表示算法所得非支配解集的数目,vi表示第i个解构成的超立方体。HV值越大,表示算法的优化结果越好。
HV=δ(∪|S|i=1vi)。(2)
2.3 消融实验
在进化算法中,平衡种群的多样性和收敛性是十分重要的,在填充准则中选择不确定度较小的个体进行真实计算有助于改善种群的收敛性,选择不确定度较大的个体进行真实计算会增强种群的多样性。另外在单次选择出较多的个体进行真实计算时,不利于种群的寻优。因此,消融实验如表2所示,其中US-MOEA(Min)表示在填充准则中仅选择不确定度小的个体;US-MOEA(Max)表示在填充准则中仅选择不确定度大的个体;US-MOEA(All)表示在填充准则中依据所有的目标函数选择个体。并且选择测试种群收敛性的DTLZ1函数,测试种群多样性的DTLZ4函数上进行比较。从中可以看出,US-MOE A(Min)在DTLZ1函数相较于US-MOEA表现较好,在DTLZ4上表现较差,其主要原因为,选择不确定度小的个体有助于增强种群的收敛性。US-MOEA(Max)在DTLZ4上表现较好,原因为选择不确定度大的个体进行真实计算增强种群的多样性。US-MOEA (All)在12和14个目标上表现较差,我们认为其主要原因在单次填充准则中选择较多的个体进行真实计算不利于算法解决昂贵高维多目标优化问题。
当训练样本的数量较多时,高斯过程模型的计算复杂度会变大,因此,在US-MOEA中提出使用基于非支配排序的样本选择方法。为了验证该策略的有效性,设计如下对比试验,其中US-MOEA(AllData)表示选用数据库中所有样本建立模型。表3给出了2种算法在DTLZ1函数上的IGD统计结果和运行时间统计表。从中可以看出US-MOEA(AllData)在3和6个目标上表现较好,在10、12和14个目标上没有显著性差异。然而,在运行时间上US-MOEA则有显著优势。综上,当采用非支配排序的样本选择方法时,显著降低算法的计算復杂度,并且算法的优化结果并没有显著变差。
2.4 对比算法及US-MOEA在DTLZ函数结果分析
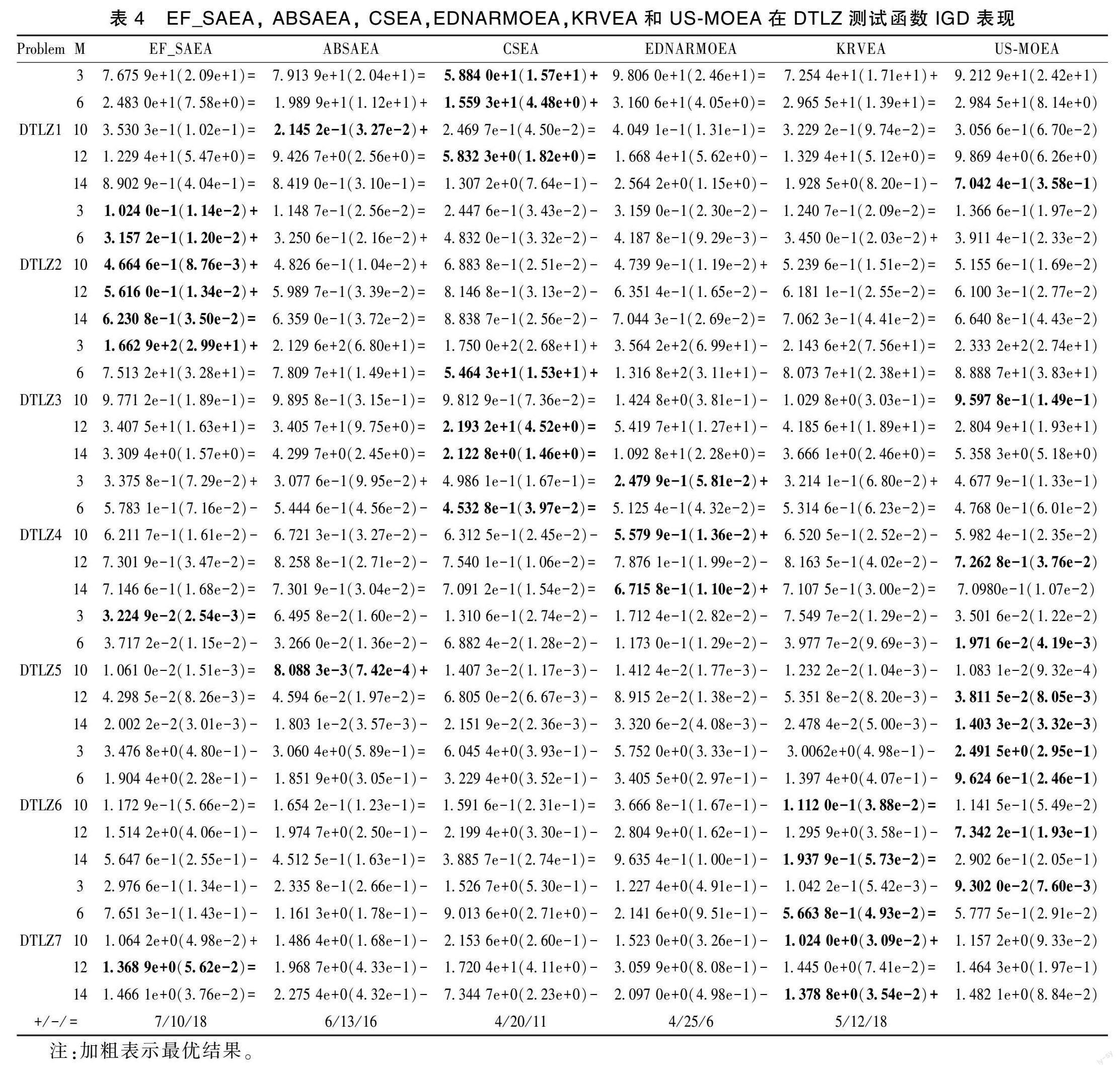
为了验证本文提出算法在解决昂贵高维多目标优化问题的有效性,在DTLZ测试函数上分别测试3、6、10、12、14个目标函数,并且分别和近些年提出的5个具有代表性的同类型算法进行比较,其中,5个对比算法分别为EF_SAEA、ABSAEA、CSEA、EDNARMOEA、KRVEA。从表4中最后一行可以看出本文提出US-MOEA算法相较于EF_SAEA、ABSAEA、CSEA、 EDNARMOEA、KRVEA表现较好的测试函数个数为10、13、20、25、12,表现较差的函数个数为7、6、4、4、5。通过对比实验结果可以发现,本文提出的US-MOEA算法在解决昂贵高维多目标优化问题中相较于其他同类型算法更有优势。另外从表中我们可以看出EF_SAEA算法在DTLZ2函数上表现最好,其主要原因为该算法采用了由3个模型构成的集成模型,且该3个子模型是由待优化问题的不同维度构成的,因此,集成模型可以更加准确的拟合待优化目标函数,有利于种群寻优。US-MOEA算法在相较于其他算法在DTLZ5和DTLZ6上表现更优,其主要原因为本文提出的填充准则可以合理的平衡种群的多样性和收敛性,更有利于种群的寻优。
2.5 对比算法及US-MOEA在WFG函数结果分析
为了验证算法在解决昂贵高维多目标优化问题的有效性,选择测试算法在WFG测试函数12和14个目标函数性能。从表5中可以看出US-MOEA相较于EF_SAEA、ABSAEA、CSEA、EDNARMOEA、KRVEA表现好的函数个数分别为3、11、14、11、8,表现较差的函数个数为0、1、1、0、0。从中可以看出算法US-MOEA在解决昂贵高维多目标优化问题中更有优势。另外值得注意的是,EF_SAEA在WFG测试函数的表现较好,其主要原因是优秀的建模策略,因此希望提出新的建模策略可以更好的拟合目标函数。
3 结论
本文提出了基于估值不确定度的昂贵多目标优化算法,在该算法中使用高斯過程拟合待优化的昂贵目标函数,采用RVEA算法对高斯过程模型寻优,通过填充准则选择恰当的解进行真实计算。在填充准则中,常采用个体不确定度均值不能恰当反映该个体的所有估值的不确定度信息。
针对该问题,本文提出依据每个目标不确定度填充采用规则,为了平衡种群多样性和收敛性,随机选择每个目标不确定度估值的最大或者最小的个体。
另外,当解决昂贵高维多目标优化问题时,为了避免单次进化过程中选择过多的解进行真实评价,可随机选择一半的目标函数,并且依据该目标函数选择解。在DTLZ和WFG测试函数的实验结果表明,US-MOEA相较于5种同类型算法更适合解决昂贵多目标优化问题。
模型的泛化性能随着决策空间维度的升高而急剧下降,下一步提出优秀的建模方法用于高维优化问题,如改进适用于高维优化问题的种群进化方法和相应的填充准则。
参考文献(References)
[1] DONG Y C, ZHANG H L, WANG C, et al. Wind power forecasting based on stacking ensemble model, decomposition and intelligent optimization algorithm[J]. Neurocomputing, 2021, 462: 169-184.
[2] 王敏, 陈峰, 张磊石. 具有反向学习能力的串车调度算法研究[J]. 交通运输系统工程与信息, 2019, 19(2): 102-107,115.
WANG M,CHEN F,ZHANG L S. Tandem scheduling algorithm on Opposition-learning[J]. Journal of Transportation Systems Engineering and Information Technology, 2019, 19(2): 102-107,115.
[3] WANG H, SUN C L, ZHANG G C, et al. Non-dominated sorting on performance indicators for evolutionary many-objective optimization[J]. Information Sciences, 2021, 551: 23-38.
[4] WANG H, SUN C L, YU H B, et al. A decomposition-based many-objective evolutionary algorithm with optional performance indicators[J]. Complex Intelligent Systems, 2022, 8(6): 5157-5176.
[5] ZHOU J J, RAO S J, GAO L, et al. Self-regulated bi-partitioning evolution for many-objective optimization[J]. Information Sciences, 2022, 589: 827-848.
[6] SONG Z S, WANG H D, HE C, et al. A Kriging-assisted two-archive evolutionary algorithm for expensive many-objective optimization[J]. IEEE Transactions on Evolutionary Computation, 2021, 25(6): 1013-1027.
[7] KNOWLES J D. ParEGO: A hybrid algorithm with on-line landscape approximation for expensive multiobjective optimization problems[J]. IEEE Transactions on Evolutionary Computation, 2006, 10(1): 50-66.
[8] ZHANG J Y, ZHOU A M, ZHANG G X. A classification and Pareto domination based multiobjective evolutionary algorithm[C]∥2015 IEEE Congress on Evolutionary Computation (CEC), 2015.
[9] PAN L Q, HE C, TIAN Y, et al. A classification-based surrogate-assisted evolutionary algorithm for expensive many-objective optimization[J]. IEEE Transactions on Evolutionary Computation, 2019, 23(1): 74-88.
[10] CHUGH T, JIN Y C, MIETTINEN K, et al. A surrogate-assisted reference vector guided evolutionary algorithm for computationally expensive many-objective optimization[J]. IEEE Transactions on Evolutionary Computation, 2018, 22(1): 129-142.
[11] GUO D, WANG X L, GAO K L, et al. Evolutionary optimization of high-dimensional multiobjective and many-objective expensive problems assisted by a dropout neural network[J]. IEEE Transactions on Systems, Man, and Cybernetics: Systems, 2022, 52(4): 2084-2097.
[12] WANG H, LIANG M N, SUN C L, et al. Multiple-strategy learning particle swarm optimization for large-scale optimization problems[J]. Complex Intelligent Systems, 2021, 7(1): 1-16.
[13] DEB K, THIELE L, LAUMANNS M, et al. Scalable multi-objective optimization test problems[C]∥2002 Congress on Evolutionary Computation, 2002.
[14] HUBAND S, HINGSTON P, BARONE L. While Lyndon A review of multiobjective test problems and a scalable test problem toolkit[J]. IEEE Transactions on Evolutionary Computation, 2006, 10(5): 477-506.
[15] ISHIBUCHI H, MASUDA H, TANIGAKI Y, et al. Modified distance calculation in generational distance and inverted generational distance[C]∥proceedings of the International conference on evolutionary multi-criterion optimization, F, 2015. Springer.
(責任编辑:编辑郭芸婕)

