考虑波形腹板剪切的端部固支组合梁挠度分析
王启飞 刘应该 王志宇 向思杰 彭志强 曾维唯
摘要:波形鋼腹板组合梁因其优良性能得到广泛应用,其挠度问题是研究的重点之一,近年来我国对波形钢腹板组合梁挠度计算方法的研究虽有长足的进步,但多集中于静定结构,并且端部固支的超静定结构体系在桥梁工程中应用广泛。为了探讨不同支承下波形钢腹板组合梁滑移附加挠度变化的规律,并为波形钢腹板组合梁的后续研究提供理论基础和参考,在足够刚度的前提下将端部固支波形钢腹板梁简化为两端固支和一端固支一端活动铰支的端部约束条件,推导了其考虑滑移和腹板剪切变形影响时的跨中挠度计算公式,找到适用于实际桥型的挠度计算方法;基于试验梁和有限元模型对本文公式进行了验证,结果表明:端部固支波形钢腹板组合梁的滑移附加挠度占比随剪切刚度的变化趋势显著区别于一端固定铰支一端活动铰支的抛物线型而呈线性变化;不对称约束放大了波形钢腹板组合梁腹板的剪切变形和滑移效应。
关键词:波形钢腹板组合梁;界面滑移效应;剪切变形;挠度
中图分类号:U448.21文献标志码:A文献标识码
Analysis on the deflection of fixed composite beam with corrugated steel webs considering the effect of shear deformation
WANG Qifei1,LIU Yinggai2,WANG Zhiyu1*,XIANG Sijie3,PENG Zhiqiang2,ZENG Weiwei2
(1 Department of Civil Engineering,College of Architecture and Environment,Sichuan University,Chengdu,Sichuan 610065,China;
2 CREGC Architectural & Construction Engineering Co.Ltd.,Chengdu,Sichuan 610031,China;
3 State Key Laboratory of Mountain Bridge and Tunnel Engineering Co-built by Provincial and Ministry,Chongqing Jiaotong
University,Chongqing 400074,China)
Abstract: Composite beam with corrugated steel webs are widely used because of their excellent properties.Although the research on deflection calculation of composite beam with corrugated steel webs which is one of the focuses of its research in China has made great progress in recent years,but only statically determinate structures are considered,and the widely use of statically indeterminate structures with fixed ends in bridge engineering.In order to discuss the deflection of fixed composite beam with corrugated steel webs and provide theoretical basis and guidance for follow-up study,this paper assumes that joint stiffness is large enough,the composite beam with corrugated steel webs will be simplified as two fixed ends or one end fixed and the other hinged,considering the influence of slip and web shear deformation,the corresponding formula of midspan deflection is derived.It is hoped that the deflection calculation method suitable for the actual bridge type will be found step by step.Based on test beam and finite element model,the formula in this paper is verified.The results show that:the proportion of additional slip deflection of composite beams with corrugated steel webs fixed at the ends varies linearly with shear stiffness,which is significantly different from that of parabolic pattern of beams with simply supported ends.The asymmetrical support magnifies the shear deformation and slip effect of composite beams with corrugated steel webs.
Key words: composite beam with corrugated steel webs;interface slip effect;shear deformation;deflection
采用波形钢腹板取代平腹板的波形钢腹板组合梁具有降低自重、提高预应力施加效率、避免腹板开裂等优点,近年在国内外发展迅速[1-2]。腹板厚度及形状的变化同时带来了褶皱效应[3],致使抗剪剛度明显降低,腹板的剪切变形相较于普通组合梁不可忽略。上部结构在行车荷载下产生的下挠是不可避免的,过大的挠度不仅影响正常行车,还会令混凝土结构开裂,降低截面承载力,带来安全隐患。
国内外学者对波形钢腹板组合梁桥的变形进行了大量的试验和理论研究,其中:李宏江等[4]以Timoshenko理论为基础,推导出集中力下简支梁跨中挠度的计算公式,依托试验和有限元模型证明了考虑腹板剪切变形的必要性;贺君等[5]根据腹板转角、顶底板转角与挠度关系得到了对称荷载下简支梁的跨中挠度计算方法及其适用范围,其后续的研究[6]表明设置内衬混凝土对挠度的影响较小;聂建国等[7]将波形钢腹板梁的变形分解为桁架作用和弯曲作用,建立了考虑腹板剪切变形的理论模型,并按结果等效的原理提出了简支梁和悬臂梁挠度计算的有效刚度法[8];叶华文等[9]对波形钢腹板梁的挠曲线进行拟合,基于最小势能原理提出了简支梁和悬臂梁跨中挠度的三角级数解,并给出了考虑剪切变形的高跨比界限;陈夏春等[10]提出了波形钢腹板梁的“夹层梁理论模型”,之后以挠度为自变量推导了Timoshenko理论下考虑耦合作用的控制微分方程[11];冯建祥等[12]将变形分解为主弯曲和次弯曲,以腹板额外剪切变形来代替滑移,推导了考虑波形钢腹板剪切变形及界面滑移的弹性弯曲微分方程,得出“横隔板对梁体变形影响很小”的结论;Zhang等[13]结合zig-zag变形假设[14],利用变分原理得到了控制方程和特定边界条件下的挠度函数。然而,这些文献中的简化公式都仅考虑了简支和悬臂两种边界条件,其他端部约束下只给出了统一的控制方程,未言明求解所需的边界条件和具体参数,因此存在难以推广到实际工程的问题。
我国CECS 291—2011《波纹腹板钢结构技术规程》针对房建工程给出了波形钢腹板梁在两端固支约束下的挠度计算公式,DB14/T 1552—2017《公路波形钢腹板组合箱梁桥设计规范》则要求“波形钢腹板预应力混凝土箱梁的变形验算按JTG D62—2004中的6.5条规定进行”并采用沿腹板波形进行积分运算的方法计入腹板的剪切变形。可见,现有规范虽对腹板剪切变形进行了考虑,但分别由于针对性和不便于准确计算最大挠度值而限制了其应用。在工程实践中,梁端常采用的边界条件有铰接、固定和自由[13],因此有必要在对静定波形钢腹板组合梁挠度研究较充分的现状下,填补端部固支的超静定波形钢腹板组合梁挠度问题研究上的欠缺,为新一轮规范修订提供参考。本文以变形协调为基础,在考虑剪切变形及滑移影响的前提下推导了跨中集中力下两端固支及一端固支一端活动铰支的波形钢腹板组合梁跨中挠度计算公式,再通过静载受弯试验研究不同边界条件下的弯曲行为,并利用有限元进行参数分析。
1 波形钢腹板梁挠度的理论分析
1.1 计算假定
(1)梁体竖向不可压缩,顶底板和波形腹板均为理想线弹性材料,各隔离体的曲率相等[7]。
(2)忽略顶底板的剪切变形,忽略腹板弯曲变形而考虑其剪切变形[8]。
(3)界面剪应力与滑移呈线性关系[12]。
(4)仅考虑荷载平面内的变形和支座约束情况。
1.2 波形钢腹板梁挠度表达式
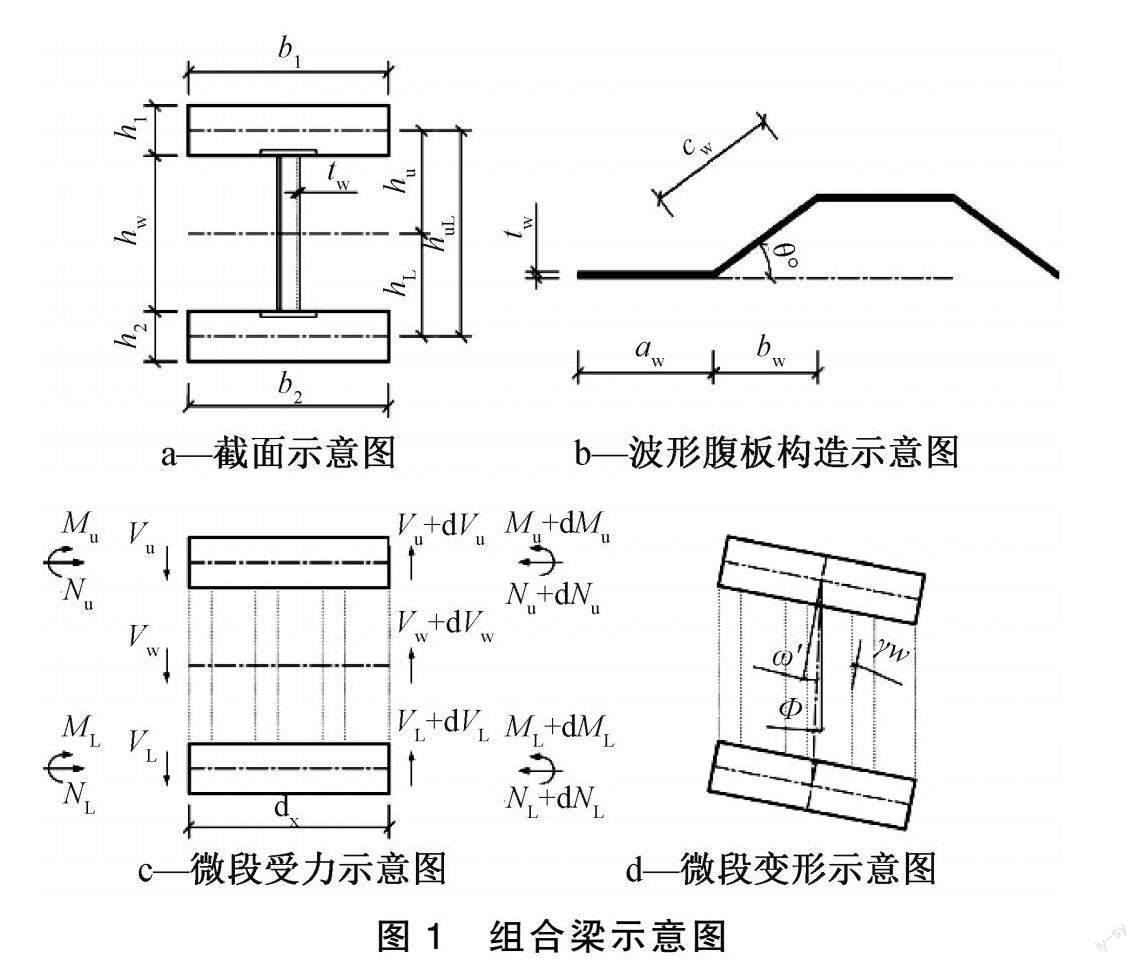
波形钢腹板组合梁中混凝土顶底板和波形钢腹板由剪力连接件组合在一起共同工作。不考虑滑移效应时,挠度主要由顶底板弯曲变形和腹板剪切变形2项组成。组合梁参数、微段受力模式及变形如图1所示,其中:Nu和NL分别为顶板和底板轴力;hu和hL分别为顶板和底板自身与全截面的形心距;Mu和ML分别为顶板和底板弯矩;Φ为顶底板转角;ω为组合梁挠度;Vu、Vw和VL分别为顶板、腹板和底板剪力;hw、tw分别为腹板高度和厚度;huL=hu+hL;γw为腹板的剪切变形;aw为波形腹板的直板段长度、bw为斜板段水平投影长度、cw为斜板段长度。
对文献[8]依据轴力与腹板剪力的关系得到以挠度ω和顶底板转角Φ为变量的控制方程,在对控制方程推演后可得到挠度ω(x)和顶底板转角Φ(x)解的表达式:
ω(x)=BgCα-1α3[C1cosh(αx)+C2sinh(αx)]-12C3x2-C4x+C5+Cv,(1)
Φ(x)=C1sinh(αx)α2+C2cosh(αx)α2+C3x+C4+V(x)(Bg+Bf)dxdx,(2)
以上公式中C=GefftwhuL,其中Geff为腹板等效剪切模量,由波形腹板的剪切模量Gs按公式Geff=Gs(aw+bw)/(aw+cw)计算;α=(C(Bg+Bf)/BgBf)0.5;Bg=EcAuhu2+EcALhL2;Ec为混凝土弹性模量;Au和AL分别为顶板和底板面积;Bf=EcIu+EcIL;Iu和IL分别为顶板和底板对自身的惯性矩;P为跨中集中荷载;L为组合梁的计算跨度;C1到C5为未知系数,由不同约束所对应的边界条件求解;Cv为控制方程的特解,与不同约束条件下的剪力分布有关。
本文涉及的与约束有关的梁端支座类型参照文献[15]共有以下3种:
(1) 固定铰支:约束梁沿轴向和竖向位移的结构部位。
(2) 活动铰支:约束梁沿竖向位移的结构部位。
(3) 固支:约束梁沿轴向和竖向位移及荷载平面内转动的结构部位。
1.3 波形钢腹板梁挠度解
1.3.1 一端固定铰支一端活动铰支
针对一端固定铰支一端活动铰支的端部约束条件,文献[8]给出了该条件下波形钢腹板梁承受跨中集中荷载时跨中挠度计算公式。
1.3.2 两端固支波形钢腹板梁挠度解
针对两端固支的端部约束条件,波形钢腹板梁承受跨中集中荷载时,梁的剪力分布和边界条件为:
V(x)=P2,0≤x -P2,L2≤x ω(0)=0;(L2)=0;M(0)=-PL8 ω′(0)=0;(0)=0;M(L2)=PL8,(4) 按截面剪力分布(3)和边界条件式(4),结合表达式(1)和(2)可求得: C1=[P(1-cosh(αL/2))]/[2(Bg+Bf)sinh(αL/2); C2=P/[2(Bg+Bf)]; C3=PL/[8(Bg+Bf)]; C4=-P/[2α2(Bg+Bf)]; C5=[P(1-α2Bg)(1-cosh(αL/2))]/[2α3(Bg+Bf)sinh(αL/2)]; Cv=Px3/[12(Bg+Bf)]-BgPx/[2C(Bg+Bf)]。 将以上系数代入式(1)便得到两端固支波形钢腹板梁在集中荷载下跨中挠度: wL2=PL3192(Bg+Bf)+PL(Bgα2-C)4Cα2(Bg+Bf)+P(C-Bgα2)coshαL2-1(Bg+Bf)Cα3sinhαL2。(5) 1.3.3 一端固支一端活动铰支波形钢腹板梁挠度解 针对一端固支一端活动铰支的端部约束条件,其约束能力居于前两种之间,且具有不对称性,令跨中顶底板转角为θ,梁的剪力分布和边界条件可表示为: V(x)=11P16,0≤x -5P16,L2≤x ω(0)=0;L2=θ;M(0)=-3PL16 ω′(0)=0;(0)=0;ML2=5PL32,(7) 重复1.4节的步骤,得该边界条件各系数如下所示:C1=[α(θ+PL2/128(Bg+Bf))+C2(1-cosh(αL/2))]/sinh(αL/2);C2=11P/[16(Bg+Bf)];C3=3PL/[16(Bg+Bf)];C4=-11P/[16α2(Bg+Bf)];C5=C1[(1-α2Bg)/α3(Bg+Bf)];Cv=11Px3/[96(Bg+Bf)]-11BgPx/[16C(Bg+Bf)]。由于ɑ[θ+PL2/128(Bg+Bf)]远小于sinh(ɑL/2),简化后将各系数代入式(1)可得一端固支一端活动铰支波形钢腹板梁在集中荷載下跨中挠度: wL2=7PL3768(Bg+Bf)+11PL(Bgα2-C)32Cα2(Bg+Bf)+11P(C-Bgα2)coshαL2-116(Bg+Bf)Cα3sinhαL2。(8) 由式(5)、(8)可知:不考虑滑移效应时,不同端部约束下的波形钢腹板组合梁跨中挠度表达式均由3项组成,第1项为顶底板弯曲变形,其系数与Euler理论相同,第2项为波形腹板剪切变形,相同荷载下两端固支和一端固定铰支一端活动铰支梁的数值相等,与CECS 291—2011《波纹腹板钢结构技术规程》相吻合;第3项为顶底板与腹板变形的耦合作用,对挠度的贡献为负值。 1.4 考虑滑移效应的波形钢腹板梁挠度 本文基于文献[12]中滑移与腹板剪应变的关系研究滑移效应对挠度的影响,腹板受力情况及剪切变形如图2所示,其中Su和SL分别为上滑移面和下滑移面的滑移,бu和бL分别为腹板上界面和下界面正应力,qu和qL分别为上界面和下界面剪力流。文献[12]令腹板的剪应力由剪力件连续化后的上滑移面剪力流qu和下滑移面剪力流qL的表达形式与腹板剪切变形表达式形式一致得到折减系数Ks。 Ks取值在0~1之间,Ks越大,连接刚度越强。在得到折减系数Ks后,只需将式(5)、(8)中的腹板折减刚度C替换为KsC便可得到对应条件下考虑滑移效应的跨中挠度表达式。 1.5 规范公式 CECS 291—2011《波纹腹板钢结构技术规程》将挠度分为两部分-翼缘板弯曲变形(认为翼缘承担全部弯矩),以及波形钢腹板剪切变形(认为腹板承担全部剪力),给出了一端固定铰支一端活动铰支和两端固支波形钢腹板梁在集中力下不考虑滑移效应的跨中挠度计算公式。 2 波形钢腹板组合梁三点弯曲试验 2.1 试件尺寸与参数 为研究波形钢腹板组合梁在不同边界条件下的弯曲性能,对1根波形钢腹板组合梁试件进行三点弯曲试验。试验梁全长1 765mm,计算跨度1 735mm,试件几何尺寸如图3所示。混凝土顶、底板内部各配有4根直径6mm的螺纹钢筋,支座和跨中部位设置混凝土墩台以防止腹板屈曲,各材料力学性能如表1所示。 2.2 试验加载与量测 试验采用Servotest多功能伺服动静力加载试验系统在跨中施加集中荷载,加载过程采用力控制,荷载分级为2 kN,加载速率为0.4 kN/min,在达到20 kN后以相同方式卸载。试件两端分别采用辊轴和固定铰支座来模拟一端固定铰支一端活动铰支梁,采用夹支支座来模拟两端固支梁,试验梁布置如图4所示。试验中采用恒量带钻千分表测量跨中下方的位移,千分表布置见图5,量测结果由JM3812系统采集。 2.3 试验结果与分析 采用CECS 291—2011《波纹腹板钢结构技术规程》中公式(简称为规范公式)和本文1.3~1.5节公式(简称为本文公式)计算试验梁在不同端部约束下的挠度,对比试验结果和验证本文公式的计算精度和实用性。计算时不计波形钢腹板翼缘抗弯能力并考虑波形腹板0.5mm的锈蚀厚度,由计算结果(表2)可见:一端固定铰支一端活动铰支的端部约束下,规范公式和本文公式理论解与试验结果的误差相近,均在10%以内;两端固支的端部约束下,本文公式与实验值的吻合度优于规范公式。其原因分析如下:试验梁的剪力连接刚度较小,由此引起的一端固定铰支一端活动铰支的端部约束下较大的滑移附加挠度对规范公式中简化的计算条件进行了补偿,而固支下相对较小的滑移附加挠度令规范公式的精确度进一步下降。 综上所述,在计算采用剪力件连接的波形钢腹板组合梁的挠度时,若忽略界面滑移效应的影响而直接按规范公式计算会产生较大的误差,相对于规范公式而言,本文公式更适用于考虑界面滑移效应时波形钢腹板组合梁挠度的计算。 3 有限元分析 3.1 有限元模型建立 为验证本文得出的挠度计算公式,采用Midas FEA NX软件进行有限元分析,按表1材料参数建立的波形钢腹板组合梁有限元模型如图6所示,钢材与混凝土均为三维实体单元,以自动网格方式进行网格划分,单元整体网格尺寸为30mm。在试验荷载下材料始终处于线弹性状态,故有限元模型分析的类型选用“线性静力分析”,且通过一次分析就能求得挠度结果。 3.2 边界条件模拟 根据试验梁边界条件类型,对图6模型的对应位置施加表3中的约束,其中ux、uy和uz分别对应沿x、y和z轴的位移,θx、θy和θz为绕相应轴的转角。 3.3 滑移效应模拟 模型分为考虑滑移效应和不考虑滑移效应2种工况。不考虑滑移效应时,钢腹板与混凝土“面面接触”部分定义为完全刚性的共节点连接,考虑滑移效应时,对腹板及顶底板剪力件对应位置采用“点印刻”功能布置接触点位,网格划分后以弹性连接对剪力件进行模拟。计算模型中只考虑剪力件的剪切变形,并忽略顶底板与腹板之间的掀起,故取弹性连接x方向刚度为剪力连接件刚度ku(kL),其余方向均按刚接处理。与不考虑滑移效应的模型相比,考虑滑移效应时钢腹板与混凝土仅在剪力件对应节点处设置弹簧单元,“面面接触”的其他部位不设连接。 3.4 有限元模型验证 对文献[4]和本文中模型试验梁的结果进行对比,验证所建立的波形钢腹板组合梁有限元模型的准确性。试验对象分别是一端固定铰支一端活动铰支和两端固支的端部约束下的波形钢腹板组合梁,对组合梁跨中单点加载下的挠度研究。按上述方案建立有限元分析模型,提取梁在20 kN集中荷载下的跨中挠度,结果(表4)显示有限元结果与试验结果吻合良好,表明本文建立有限元模型的方法准确、有效。 3.5 参数分析 为研究采用本文公式计算波形钢腹板组合梁挠度的可行性,并给出高跨比对规范公式和本文公式精度的影响,在截面高度不变下,跨度分别取1 150、1 725、2 300、2 875、3 450、4 025、4 600mm,P=20 kN。根据几何尺寸建立有限元模型,端部约束类型按一端固定铰支一端活动铰支、两端固支和一端固支一端活动铰支考虑,按规范公式、本文公式及有限元法得到的不同跨高比下不考虑滑移效应(Ks=1)和考慮滑移效应(Ks=0.7)下的挠度见表5。 由表5可知: (1)不考虑滑移效应时,规范公式的理论值与有限元值的误差随跨高比的增大而逐渐减小,在L/H=20时,规范公式的理论值与有限元结果的误差在一端固定铰支一端活动铰支时为7%,两端固支时为11%。本文公式的理论值与有限元值的误差始终在10%以内,其中:在一端固定铰支一端活动铰支的端部约束下,本文公式的理论值与有限元值的误差随跨高比的增加而逐渐增加,最终稳定在4%左右;在两端固支的端部约束下,本文公式的理论值与有限元值的误差随跨高比的增大呈先增大后减小的趋势,在L/H=7.5时误差取得最大值5%;在一端固支一端活动铰支的端部约束下,本文公式的理论值与有限元值的误差随跨高比的增大呈先增大后减小之后再增大的趋势,在L/H=10时误差取得最大值10%。 (2)以系数Ks对腹板刚度C进行折减来考虑滑移效应时,3种端部约束下的滑移附加挠度都随跨高比的增加而增加,且跨高比每增加2.5,一端固定铰支一端活动铰支和两端固支端部约束下的滑移附加挠度增加0.05mm左右,一端固支一端活动铰支端部约束下的滑移附加挠度增加0.08mm左右。 在一端固定铰支一端活动铰支的端部约束下,总挠度的理论值与有限元值的误差随跨高比的增大呈先减小后增大的趋势,在L/H=5时总挠度的误差取得最大值5%,滑移附加挠度的理论值与有限元值的误差随跨高比的增大呈先增大后减小的趋势,在L/H=10时滑移附加挠度的误差取得最大值0.085mm。 在两端固支的端部约束下,总挠度的理论值与有限元值的误差在L/H=5时取得最大值8%,之后随跨高比的增加均保持在2%左右,滑移附加挠度的理论值与有限元值的误差在L/H=15时取得最大值0.041mm,其他跨高比下均保持在0.02mm左右。 在一端固支一端活动铰支的端部约束下,总挠度的理论值与有限元值的误差随跨高比的增大呈先减小后增大的趋势,在L/H=5时误差取得最大值8%,滑移附加挠度的理论值与有限元值的误差在5<L/H<10和10<L/H<20时均随跨高比的增大逐渐增大,并在L/H=20时误差取得最大值0.099mm。 按本文公式计算得到不同Ks取值下滑移附加挠度占总挠度的比例,由结果(图7)可知:3种端部约束下的滑移附加挠度占总挠度的比例都随Ks的增大而减小,滑移附加挠度占比由大到小为一端固支一端活动铰支、两端固支和一端固定铰支一端活动铰支。两端固支和一端固支一端活动铰支端部约束下的滑移附加挠度随Ks的变化基本一致,且滑移附加挠度所占比例均大于一端固定铰支一端活动铰支;两端固支和一端固支一端活动铰支端部约束下的滑移附加挠度在Ks>0.8时占总挠度比值大于10%,一端固定铰支一端活动铰支端部约束下的滑移附加挠度占总挠度比值在Ks>0.7时大于10%。 4 结论 为建立考虑界面滑移效应的超静定波形钢腹板组合梁挠度实用计算方法,首先在CECS 291—2011《波纹腹板钢结构技术规程》的基础上考虑截面剪力分配,通过推导得出了两端固支和一端固支一端活动铰支的端部约束下波形钢腹板组合梁跨中挠度计算公式(5)和(8),之后由系数Ks对腹板刚度C进行折减来考虑滑移效应的影响,再通过试验和有限元方法对比论证了计算公式有效性和准确性,得到以下主要结论: (1)具有固支端部约束的不对称支座布置放大了波形钢腹板组合梁腹板的剪切变形和滑移效应,一端固支一端活动铰支端部约束下的波形钢腹板组合梁由腹板剪切变形引起的跨中附加挠度值为两端固支和一端固定铰支一端活动铰支端部约束下的1.3倍左右;随跨高比的增加,两端固支与一端固定铰支一端活动铰支端部约束下组合梁跨中滑移附加挠度增量基本相同,约为一端固支一端活动铰支端部约束下的跨中滑移附加挠度增量的60%。 (2)随界面剪切刚度的减弱,端部固支波形钢腹板组合梁的滑移附加挠度占比偏线性增加,而一端固定铰支一端活动铰支波形钢腹板组合梁的滑移附加挠度占比基本呈抛物线型增加;支座由“一端固支一端活动铰支”到“两端固支”的变化对减小滑移附加挠度占比提升不大。 (3)具有固支端部约束且采用不对称支座的大跨度波形钢腹板组合梁,可通过考虑增加剪切连接刚度以达到与对称时一致的抗滑移性能和抗弯性能。 参考文献(References) [1] JIANG R J,AUF T K,XIAO Y F,et al.Prestressed concrete girder bridges with corrugated steel webs[J].Journal of Structural Engineering,2015,141(2):04014108. [2] WANG C,ZHANG Y L,ZHANG X,et al.Coupled bending-torsion behaviour of single-box multi-cell curved composite boxgirders with corrugated steel webs[J].Journal of Constructional Steel Research,2022,196(8):107411. [3] HADIDY A M E,HASSANEIN M F,ZHOU M.The effect of using tubular flanges in bridge girders with corrugated steel webs on their shear behaviour-A numerical study[J].Thin-Walled Structures,2018,124(2):121-135. [4] 李宏江,葉见曙,万水,等.剪切变形对波形钢腹板箱梁挠度的影响[J].交通运输工程学报,2002,2(4):17-20. LI H J,YE J S,WAN S,et al.Influence of shear deformation on deflection of box girder with corrugated steel webs[J].Journal of Traffic and Transportation Engineering,2002,2(4):17-20. [5] 贺君,刘玉擎,陈艾荣,等.折腹式组合梁桥考虑剪切变形的挠度计算[J].同济大学学报(自然科学版),2009,37(4):440-444. HE J,LIU Y Q,CHEN A R,et al.Deflection calculation of composite girder bridge with corrugated steel web with consideration of shear deformation[J].Journal of Tongji University(Natural Science),2009,37(4):440-444. [6] 贺君,刘玉擎,吕展,等.内衬混凝土对波形钢腹板组合梁桥力学性能的影响[J].桥梁建设,2017,47(4):54-59. HE J,LIU Y Q,LYU Z,et al.Effects of encased concrete on mechanical behavior of composite girder bridge with corrugated steel webs[J].Bridge Construction,2017,47(4):54-59. [7] 聂建国,李法雄.考虑腹板剪切行为的波形钢腹板梁理论模型[J].中国公路学报,2011,24(6):40-48. NIE J G,LI F X.Theory model of corrugated Steel web girder considering web shear behavior[J].China Journal of Highway and Transport,2011,24(6):40-48. [8] 聂建国,李法雄,樊健生.波形钢腹板梁变形计算的有效刚度法[J].工程力学,2012,29(8):71-79. NIE J G,LI F X,FAN J S.Effective stiffness method for calculating deflection of corrugated web girder[J].Engineering Mechanics,2012,29(8):71-79. [9] 叶华文,王力武,张庆,等.波形钢腹板组合梁弯曲变形的三角级数解[J].西南交通大学学报,2019,54(4):701-708. YE H W,WANG L W,ZHANG Q,et al.Trigonometric series solution of bending deformation for composite beam with steel corrugated webs[J].Journal of Southwest Jiaotong University,2019,54(4):701-708. [10] CHEN X C,AU F,BAI Z,et al.An extended sandwich theory for prestressed concrete bridges with corrugated steel web(s)[C]//The 2015 Conference of the International Association for Bridge and Structural Engineering,Nara:IABSE,2015:270-271. [11] 陈夏春,白植舟,姜瑞娟,等.波形钢腹板组合桥梁夹层梁模型[J].结构工程师,2021,37(1):32-42. CHEN X C,BAI Z Z,JIANG R J,et al.A sandwich beam model for composite bridges with corrugated steel webs[J].Structural Engineers,2021,37(1):32-42. [12] 冯建祥.波形钢腹板PC箱梁考虑滑移和剪切变形的长期变形试验研究[D].北京:北京交通大学,2021. [13] ZHANG Z C,LIU X L,HU L Y,et al.Zig-zag theory for concrete beams with corrugated steel webs[J].Structures Engineering,2022,258(7):114100. [14] 胡霖遠,陈伟球,张治成,等.基于Zig-zag理论的波形钢腹板梁的自由振动分析[J].浙江大学学报(工学版),2019,53(3):503-511. HU L Y,CHEN W Q,ZHANG Z C,et al.Free vibration analysis of concrete beams with corrugated steel webs based on Zig-zag theory[J].Journal of Zhejiang University (Engineering Science),2019,53(3):503-511. [15] 蒋玉川,阎慧群,徐双武,等.结构力学教程[M].北京:化学工业出版社,2014. (责任编辑:编辑张忠)

