基于连续路网环境的实体化主体路径规划算法
刘 钢, 安志镖, 张茂军, 刘 煜, 李 武
(1. 湖南理工学院信息科学与工程学院, 湖南 岳阳 414000; 2. 国防科技大学系统工程学院, 湖南 长沙 410073; 3. 湖南民族职业学院, 湖南 岳阳 414000)
0 引 言
复杂环境下的路径规划问题始终是任务规划领域研究的热点。随着环境的实时动态变化,需要同时考虑环境连续变化和规划主体大小,使得规划路径能够切实支撑规划主体顺利通过连续变化的环境。
实体化主体路径规划就是指根据主体的实体属性,规划出能够在真实环境中正常行驶的最优或可行路线。真实环境信息往往无法直接使用,所以需要对环境信息进行建模操作。周梦如等[1]提出了基于激光雷达和可见光相机的道路几何通行性分析方法,利用图像语义分割技术获得大致可通行区域,使用三维点云获取地面几何信息,并结合履带车辆的几何通行性约束和高斯混合聚类,获得道路野外环境模型。Papadakis[2]对于车辆可通行性的研究做了调查,使用激光雷达等技术获得三维地形数据,并将获得三维地形数据与车辆模型相结合进行路径规划,是越野行驶、星球探索等环境下较常用的路径规划环境建模的方法。Hosseinpoor等[3]提出语义地形分割(semantic terrain segmentation, STS)方法,通过根据不同高度分割地形,并使用深度卷积神经网络获得结果。目前,环境信息建模大多采用二元分类的方式进行,即仅将环境信息分为可通行性和不可通行性两种状态,环境信息未得到有效利用,为更有效利用环境信息,提出了连续环境建模方式。
针对路径规划的环境建模,目前主要分为栅格法和可视图法。Alireza等[4]提出以栅格为单元表示该区域环境信息。Yao等[5]针对环境特征,将栅格图中的障碍物分为静态障碍物、动态障碍物和准静态障碍物。Lozano-Perez等[6]提出以多边形描述环境边界和障碍物轮廓,即可视图法。针对路径规划的环境建模方法一般都将路径规划的实体化主体视为一个质点,但在实际应用中,将实体化主体视为一个质点将损失实体化主体的信息,所以针对主体的大小提出实体化主体连续环境模型(model continuous environment with subject objective, MCESO)构建方式。
1 MCESO
1.1 建模思路
MCESO的影响因子主要包含地形因子、植被因子、水文因子、人工设施因子和实体化主体因子。地形因子主要表示地形起伏及坡度信息;植被因子、水文因子和人工设施因子是根据实际场景地物分类信息;实体化主体因子主要考虑实体化主体的大小。实体化主体连续环境建模需要在坡度信息和地物分类信息融合的连续环境模型的基础上,通过考虑实体化主体大小膨胀操作和清除小连通区域得到MCESO,本文实体化主体以车辆为例。MCESO生成框架图如图1所示。
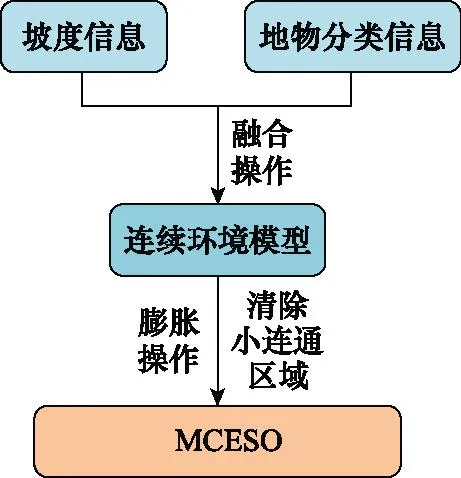
图1 MCESO框架图Fig.1 Frame diagram of MCESO
1.2 连续环境建模
为降低连续环境建模的数据存储量,将每个像素值的大小设为1 bit,其对应的数值范围为[0,255],数据应符合如下公式:
data(x,y)=m,m=0,1,…,255
(1)
式中:data表示野外环境的数据;m为0~255的正整数。
由于野外环境信息主要为坡度信息和地物分类信息,为方便使用,将数据做如下定义:
其中obstacle表示障碍:
data(x,y)=255, data(x,y)=obstacle
(2)
首先处理地形因子。地形因子主要是坡度信息,为满足式(1),坡度信息表达式为
(3)
式中:rad表示弧度制结果;int表示对括号内结果取整数部分;ang表示角度值结果。
以车辆为例,在实际行驶的过程中都存在最大坡度。当坡度大于最大坡度时可能出现侧滑情况。为避免车辆发生侧滑现象,将坡度大于最大坡度的位置设为障碍。根据式(2),坡度处理公式为
(4)
式中:slope表示处理后的坡度值;maxslope表示行驶时的最大坡度。
对于植被因子、水文因子和人工设施因子,由于数据是数字正射影像图(digital orthophoto map, DOM),需要对DOM数据做地物分类操作,然后对分类结果定性分析。根据式(2),认为植被、水体、房屋为障碍obstacle,认为道路street等为易通行。地物分类处理公式为
(5)
式中:classify表示处理后的分类结果;dom为原始的DOM数据。
通过式(4)和式(5)可以生成处理后的坡度信息和地物分类信息。对坡度信息和地物分类信息进行融合操作,即可得到最终的连续环境模型。判断公式为
(6)
式中:accessibility表示连续环境模型的栅格值;classify表示地物分类信息的栅格值;slope表示坡度信息的栅格值。
通过式(6)生成的连续环境模型充分利用坡度信息和地物分类信息的结果。
1.3 MCESO建模
通过第1.2节生成的连续环境建模考虑了坡度信息和地物分类信息对于环境模型的影响,构建连续环境模型的主要目的是为了能够在路径规划时能够充分利用环境信息。但车辆路径规划不仅要考虑自然环境对于路径规划的影响,还需要考虑车辆本身属性对于路径规划的影响。
对于车辆路径规划,需考虑的车辆属性应包含车辆大小和车辆转弯半径。由于在大范围全局路径规划时不需考虑车辆的具体姿态,所以提出在连续环境模型中加入实体化主体约束,然后在路径规划时通过利用MCESO建模得到考虑主体自身约束的规划结果。
实体化主体约束中包含实体化主体大小与转弯半径约束,其实际意义是确保实体化主体能够安全平稳的行驶。为将实体化主体约束融合到连续环境模型中,提出使用膨胀操作,将实体化主体约束融合到膨胀核中,使用膨胀操作对连续环境模型进行操作。膨胀操作示意图如图2所示,膨胀操作的公式如下:
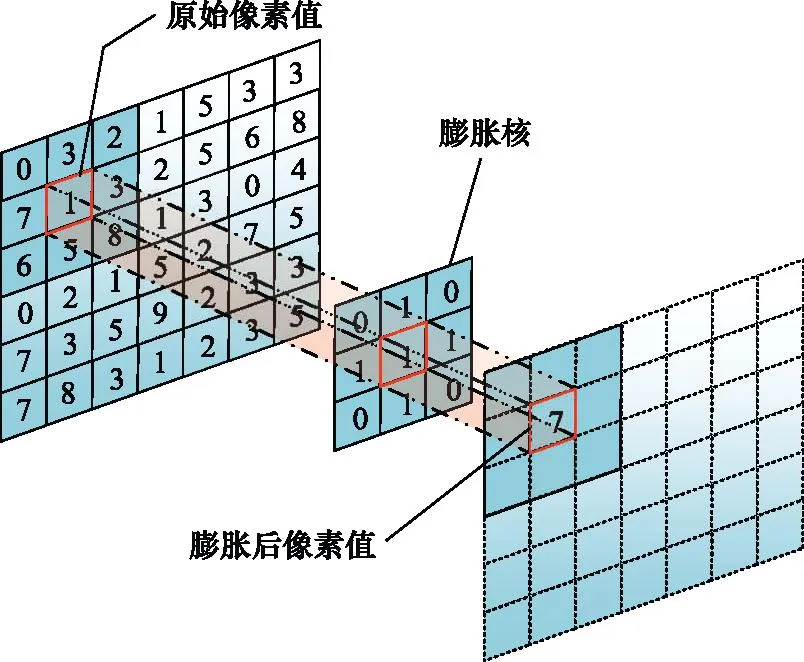
图2 膨胀操作Fig.2 Expansion operation
swell(x-a,y-a)=
(7)
式中:f(x,y)表示原始图像(x,y)位置的像素值;w(a,b)表示膨胀核(a,b)位置的像素值。
膨胀操作的核心是膨胀核的设计。膨胀核的设计以使用实体化主体大小作为基准。以车辆为例,基于设计的简单性,仅考虑车辆的8个方向。如图3所示,A、B、C、D分别表膨胀核的4个顶点;M、N、P、Q分别表示车辆的大小。其中,白色视为车辆,其像素值设为0;绿色为非车辆位置,像素值为1。由于车辆的8个方向可以认为是车辆的4个姿态,图3(a)为车身上下方向姿态;图3(b)为车身左右方向姿态;图3(c)为车身向左倾斜45°方向姿态;图3(d)为车身向右倾斜45°方向姿态。
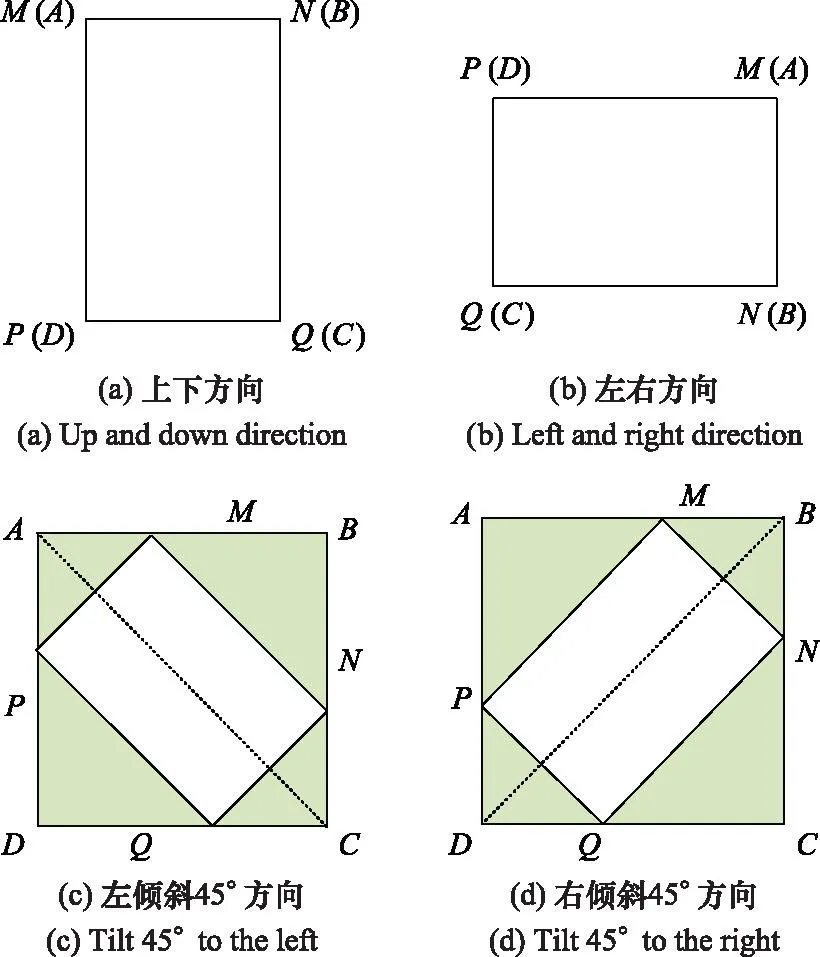
图3 膨胀核设计Fig.3 Expansion kernel design
使用图3中的所有膨胀核对连续环境模型做膨胀操作,膨胀操作的结果可以认为车辆在膨胀后的任意一点都可通行。对4个膨胀核膨胀后的结果做融合,即认为只要4个膨胀核膨胀后结果中的像素有一个点可通行,该像素点认为可通行。膨胀融合公式为
fusion(i,j)=max(fusion1(i,j),
fusion2(i,j),fusion3(i,j),
fusion4(i,j))
(8)
式中:fusion表示膨胀融合的结果;fusion1, fusion2, fusion3, fusion4分别表示对于4个膨胀核膨胀后的结果。式(8)表示当前像素点的数值为4个膨胀结果像素值的最大值。
对实体化主体连续环境建模进行膨胀操作后会出现大量小连通区域。小连通区域是指该区域不与其余区域连通,并且区域较小,该区域进行路径规划计算是不合理的,所以需要对小连通区域进行清除工作,清除小连通区域的方法如图4所示。
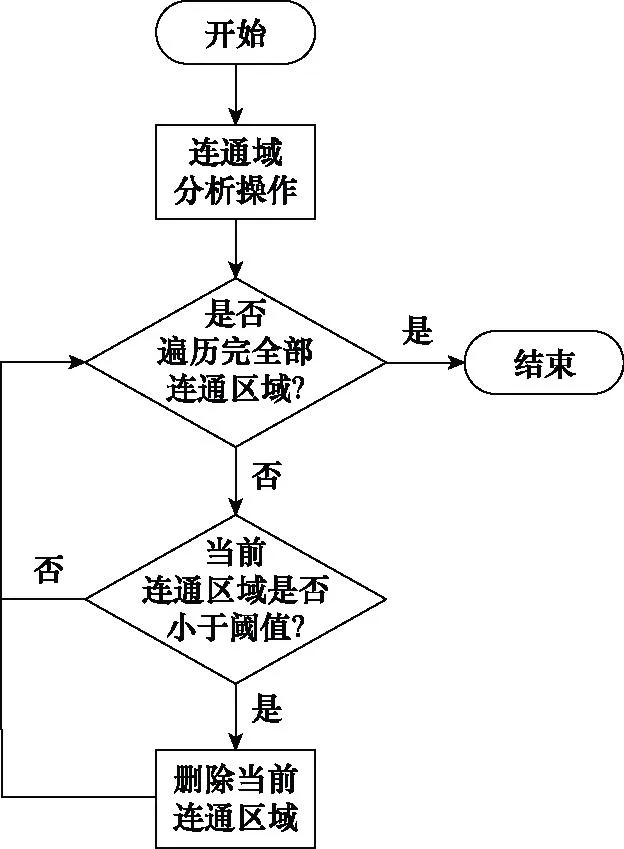
图4 清除小连通区域方法流程图Fig.4 Flowchart of clearing small connected domaining method
1.4 建模流程
实体化主体连续环境建模的构建步骤如下。
步骤 1根据数字高程模型利用坡度计算公式得到坡度信息数据。
步骤 2根据DOM利用深度学习方法得到地物分类信息数据。
步骤 3将坡度信息数据与地物分类信息数据进行融合,得到连续环境模型。
步骤 4将野外环境模型根据车辆参数信息进行膨胀操作,得到连续环境膨胀模型。
步骤 5将可通行性膨胀分析结果进行清除小连通区域操作,得到MCESO。
MCESO算法流程图如图5所示。
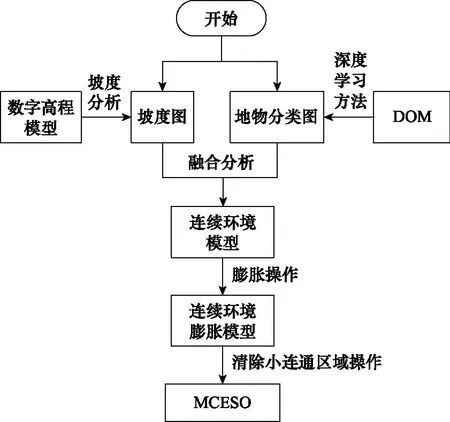
图5 MCESO流程图Fig.5 Flow chart of MCESO
2 MCESO-RNP-路径规划算法
2.1 MCESO-算法的估价函数优化
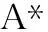
图6 MCESO示意图Fig.6 Diagram of MCESO
(9)
式中:ln-1.n表示上一个节点到当前节点的距离;ln,goal表示从当前节点到终点的距离;slope表示MCESO通过某一位置的代价;α表示对环境模型的惩罚程度。
2.2 MCESO-RNP-算法的估价函数优化
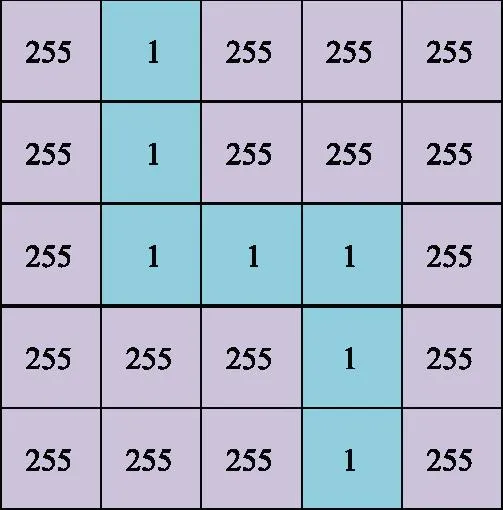
图7 道路权重图示意图Fig.7 Diagram of road weights
(10)
式中:weight表示道路权重图在某一位置的权重值。
2.3 算法流程
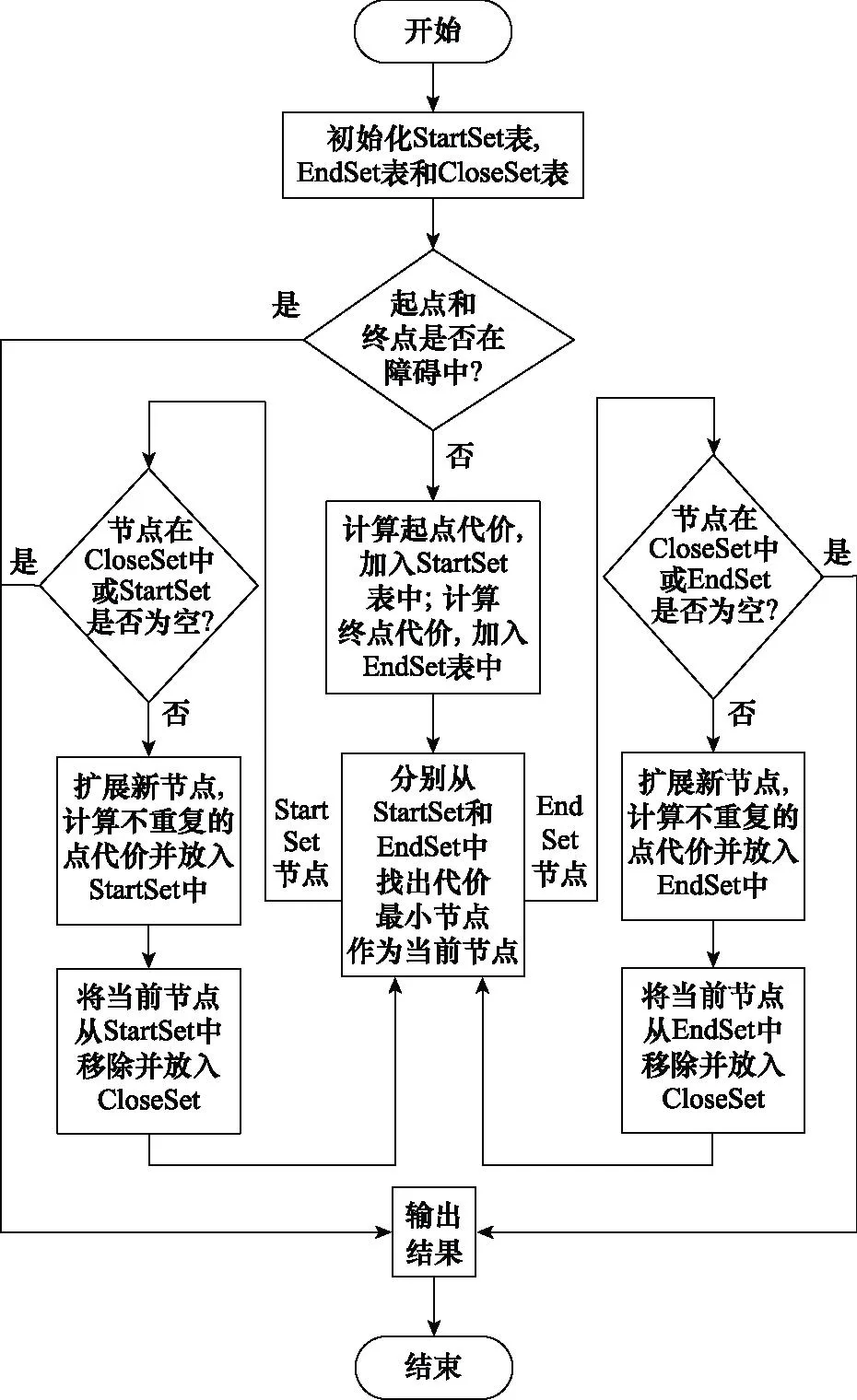
图8 MCESO-RNP-算法流程图Fig.8 Flow chart of MCESO-RNP- algorithm
算法流程如下所示。
步骤 1初始化起点列表StartSet,终点列表EndSet和搜索过的列表CloseSet。起点列表表示从起点开始搜索的OpenSet,终点列表表示从终点开始搜索的OpenSet。
步骤 3通过代价表判断起点或终点是否在障碍中。若在障碍中,则结束算法;若不在,则执行步骤4。
步骤 4将起点放入StartSet中,终点放入EndSet中,并从代价表中查出通过当前节点的代价。
步骤 5分别从StartSet和EndSet取出代价最小的节点作为当前节点,并从StartSet和EndSet删除该节点。
步骤 6判断当前节点是否相遇或StartSet、EndSet中是否为空。若相遇或为空,则执行步骤8;若否,则执行步骤7。
步骤 7使用八邻域的方式扩展当前节点,并将扩展的节点放入StartSet或EndSet中,并将当前节点放入CloseSet中,然后执行步骤5。
步骤 8从终点回溯到起点,得到最终路径。
3 仿真试验与分析
MCESO仿真分别对连续环境模型,连续环境模型膨胀后结果和MCESO进行对比。

表1 不同算法对比Table 1 Comparison of different algorithms
3.1 MCESO仿真
实验需要真实环境下的数字高程模型和DOM,实验的真实环境如图9所示,分别对真实环境中的数字高程模型和DOM进行处理。

图9 真实环境图Fig.9 Real environment diagram
将坡度图与地物分类图进行融合操作得到连续环境模型如图10所示,图中白色部分表示障碍区域,黑色表示道路,灰色部分表示该区域的坡度。构建使用车辆参数为4 m×7.5 m,构建膨胀所需的膨胀核,使用该膨胀核膨胀后的膨胀图如图11所示。从图10和图11可以看出,连续环境模型由于没有考虑运动实体大小,可通过区域明显大于使用膨胀后的结果。MCESO膨胀图如图12所示,通过图11和图12可以看出,存在小部分的非连通区域。为避免路径规划时出现非必要的路径不可通行的情况,所以对膨胀结果图进行连通性分析操作,即根据的阈值为全部面积的0.001,进行消除小连通区域操作。

图10 连续环境模型图Fig.10 Model continuous environment
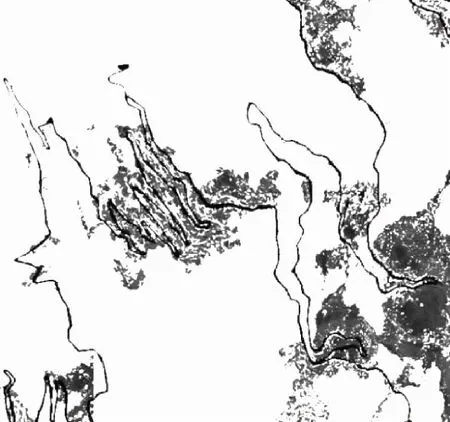
图11 连续环境建模膨胀后结果Fig.11 Model continuous environment after expansion
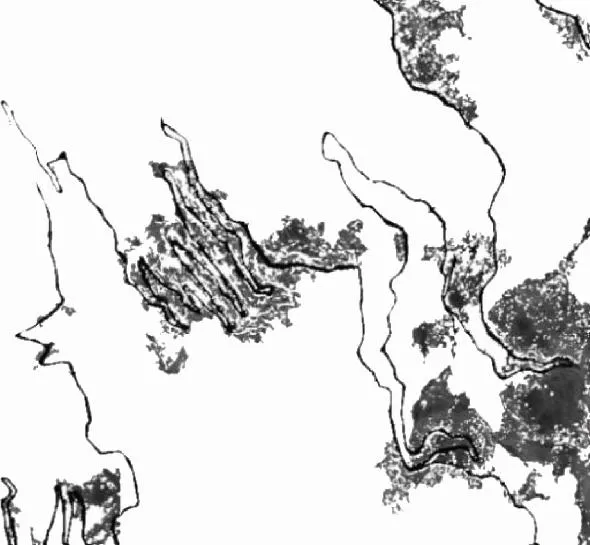
图12 MCESOFig.12 MCESO
3.2 MCESO-RNP-路径规划算法仿真
本算法考虑到环境信息的地形因素(即坡度)对路径规划结果的影响,而在大范围内无法直观感觉出地形因素的影响,所以首先在小范围内对路径规划进行三维仿真实验。仿真所用数据图如图13所示。图14为数字环境图,图15为惩罚较小时的结果图,图16为惩罚较大时的结果图。

图13 仿真数据图Fig.13 Simulation data diagram
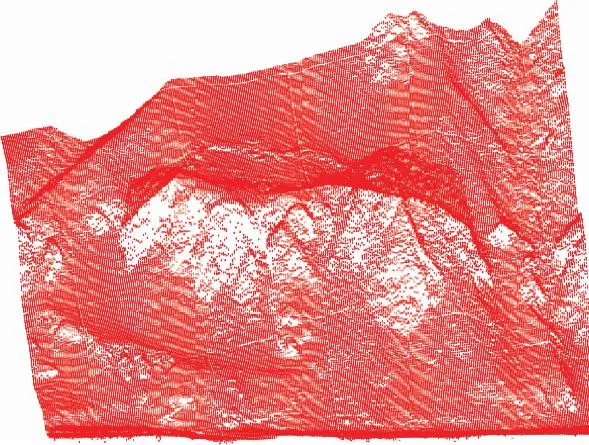
图14 数字环境图Fig.14 Digital environment diagram
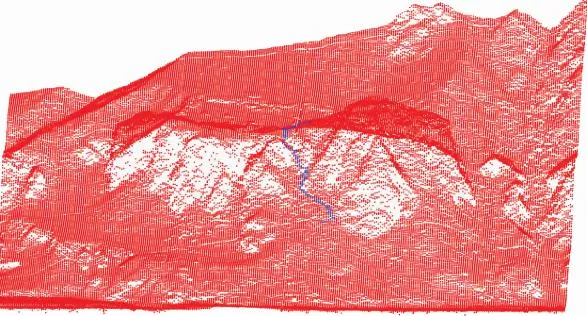
图15 惩罚值为3的结果图Fig.15 Result diagram with a penalty value of 3

图16 惩罚值为7的结果图Fig.16 Result diagram with a penalty value of 7
从图15与图16的对比明显看出,将惩罚值设置较大时可以对坡度值进行有效惩罚。并且惩罚值越大,路径规划的结果越选择更平缓的路径。通过图17结果实验对比,选择α=7作为后续实验的惩罚值。
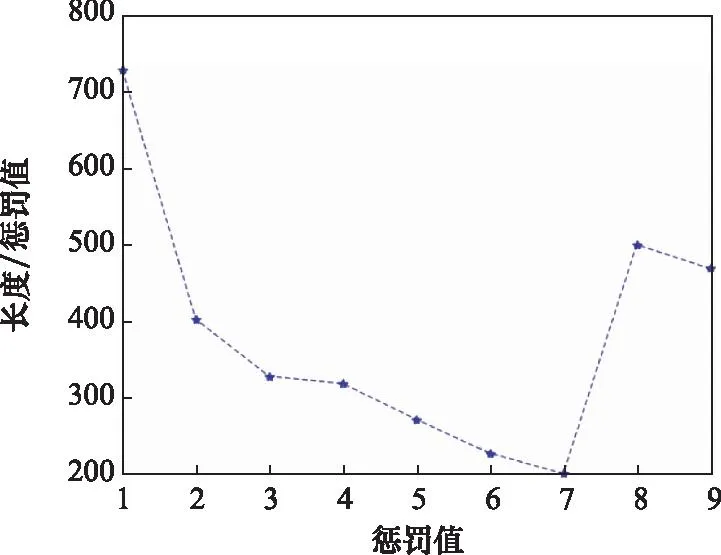
图17 路径规划长度与惩罚值比值图Fig.17 Ratio of path planning length to penalty value
在进行路径规划时使用三维展示的方式存在无法全局展示、效果不能直接对比等缺点,所以在实际仿真实验中使用二维的方式展示实验效果。
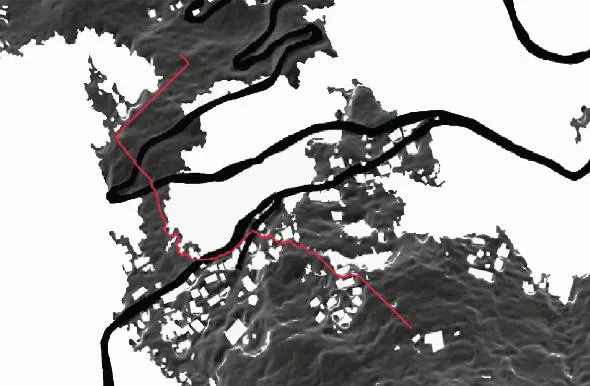
图18 MCE-算法路径规划1Fig.18 MCE- algorithm path planning 1

图19 MCE-算法路径规划2Fig.19 MCE- algorithm path planning 2
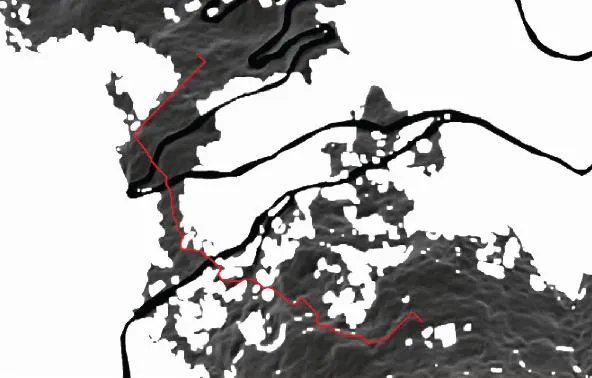
图20 MCESO-算法路径规划1Fig.20 MCESO-algorithm path planning 1
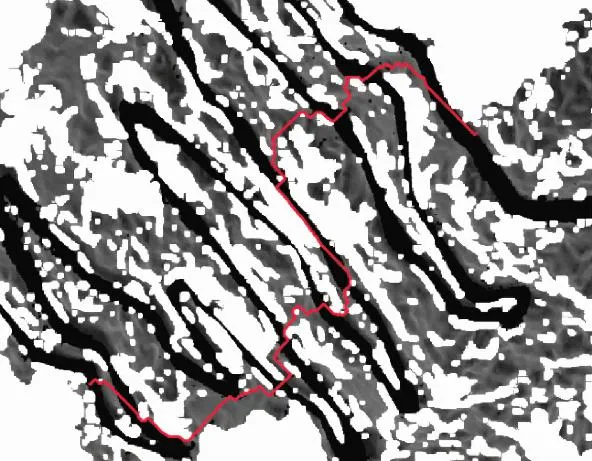
图21 MCESO-算法路径规划2Fig.21 MCESO-algorithm path planning 2

图22 道路权重图(局部)Fig.22 Road weight map (local)

图23 小范围MCESOFig.23 Small scale of MCESO
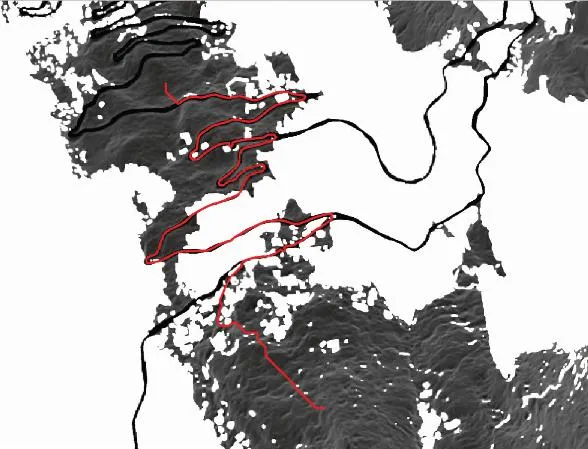
图24 MCESO-RNP-算法路径规划1Fig.24 MCESO-RNP-algorithm path planning 1
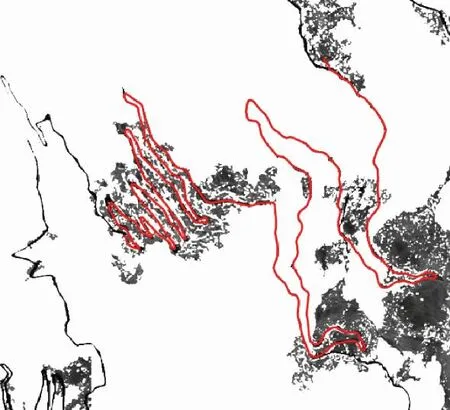
图25 MCESO-RNP-算法路径规划2Fig.25 MCESO-RNP-algorithm path planning 2
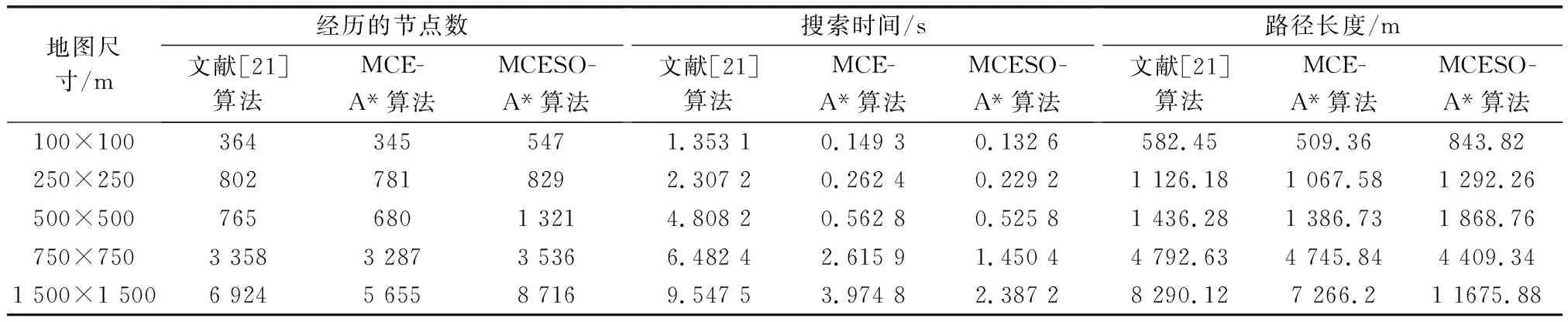
表2 不同地图下算法结果对比Table 2 Comparison of algorithm results under different maps
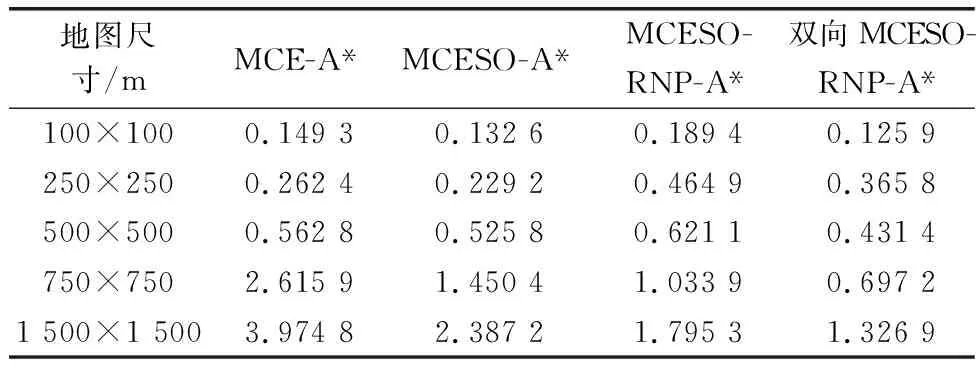
表3 不同算法时间结果对比Table 3 Comparison of time results for different algorithms s
3.3 算法性能分析与比较
对实验结果进行比较分析,得到如下结论。
(1) 针对文献[21]中的算法在计算节点代价时采用实时计算的方式,提出构建基于任务实体的连续环境建模的方式将代价融入环境模型中,提升搜索效率。
4 结束语