天波超视距雷达非均匀采样信号频谱重构
陈子睿, 陈阿磊, 刘维建, 杨 军, 陈文峰, 马晓岩
(空军预警学院, 湖北 武汉 430019)
0 引 言
天波超视距雷达(over-the-horizon radar, OTHR)作为一种特殊体制的远程预警雷达,利用电离层对电磁波的折射和反射效应,能够突破地球曲率的限制,实施视距之外的海况信息提取和舰船目标检测等任务[1-4]。与常规微波雷达相比,OTHR能够更早地发现大、中型舰船,将海面预警效率提高了30~50倍[5]。但利用OTHR快速、及时地定位海面目标需要克服许多尚未解决的难题[6]。在对海探测模式下,强大的海杂波是影响海面目标检测的主要因素,杂噪比(clutter to noise ratio, CNR)通常在50 dB以上[7-8],因此需要足够长的相参积累时间(coherent integration time, CIT)来提高信杂噪比(signal-clutter-noise ratio, SCNR)与多普勒分辨率[1]。而较长的CIT会带来两个问题[7,9]:① 对于空海探测兼容工作模式,对海探测的长CIT会导致空中目标被照射的间隔过长、数据更新率较低,不利于目标的快速跟踪。② OTHR的电波传播路径中存在严重的相位污染和瞬态干扰问题,长CIT条件下通常难以得到完整、均匀采样的有效数据。
针对上述问题,有两种解决方案:① 短CIT条件下的目标检测。通过缩减CIT克服上述问题,此方案受到CIT较短的限制,通常利用超分辨谱估计方法解决多普勒分辨率较低的问题[10],或利用杂波抑制方法抑制海杂波以凸显目标[11-13]。② 长CIT条件下非均匀采样信号的目标检测。将长CIT中受到干扰的信号或用于对空探测的信号抽出,然后通过带有缺损的非均匀采样信号重构完整频谱[14-18]。本文主要针对方案②的非均匀采样信号频谱重构问题进行研究。由于信号缺损,一般采用先对缺损信号补零、再采用快速傅里叶变换(fast Fourier transform, FFT)的方法实现,但这会导致频谱出现严重的栅瓣。为解决此问题,文献[15-16]利用海杂波与目标信号在频域上的稀疏特性,通过基于压缩感知(compressed sensing, CS)的贪婪类重构算法对非均匀采样信号进行频谱重构。此类算法在处理低维度、小尺度问题上具有较高的运算效率,但重构精度并不理想。此外,包括贪婪算法在内的大多数CS重构算法注重对稀疏信号的重构,忽略对背景特性的保留,因此通过CS重构的信号难以与现有的杂波抑制和恒虚警(constant false alarm rate, CFAR)处理方法相结合,为后续处理增加了难度[19]。文献[9]通过构造具有低秩特性的Hankel矩阵,利用非精确增广拉格朗日乘数(inexact augmented Lagrange multiplier, IALM)法实现低秩矩阵恢复(low-rank matrix recovery, LRMR)。文献[18]利用修正的奇异值阈值(singular value thresholding, SVT)算子的思想求解鲁棒主成分分析(robust principal component analysis, RPCA)问题,从而实现LRMR。LRMR类方法在缺损信号数量较少的条件下,具有较高的重构精度,而随着缺损信号数量增加,重构性能急剧下降,且此类算法较长的运算时间难以满足OTHR对实时探测的要求。
针对上述方法的不足,本文提出了一种快速自适应复近似消息传递(fast adaptive complex approximate message passing, FACAMP)频谱重构算法对非均匀采样信号进行频谱重构。首先,建立了OTHR频域信号的稀疏模型。然后,针对复近似消息传递(complex approximate message passing, CAMP)算法[20]自适应参数选择问题和重构误差问题[21],对CAMP算法进行改进,使用基于最小均方误差(minimum mean square error, MMSE)准则的复降噪函数代替复软阈值函数,并在迭代过程中自适应估计阈值参数。最后,利用FACAMP实现OTHR频谱重构,通过实测数据与现有方法对比分析其重构性能。FACAMP频谱重构算法具有以下优势:① 重构精度高。不仅能够恢复海杂波与目标信号的幅度和相位信息,而且能够保留原噪声背景的高斯性,使得重构信号能够直接与现有信号处理方案结合并进行后续处理。② 运算复杂度低。具有较快的收敛速度和较低的单次迭代复杂度,算法的运算时间能够满足OTHR对实时探测的需求。③ 自适应性强。能够在不同环境的海杂波背景和不同采样数条件下,自适应估计并选择合适的阈值参数。理论分析和仿真实验均验证了所提算法的有效性。
1 信号模型与CAMP算法
本节分别对OTHR完整和非均匀采样回波信号进行建模,阐述了如何使用CAMP解决频谱重构问题,并指出了现有方法的不足。
1.1 完整回波信号模型
信号重构实现于波束形成和匹配滤波之后,OTHR使用FFT实现相参积累,将某个距离单元的慢时间回波向量y∈CN×1变换到频域x∈CN×1,通过逆快速傅里叶变换(inverse fast Fourier transform, IFFT)得到,即y=IFFT(x),其中N为一个CIT内的脉冲个数,y可表示为
y(n)=s(n)+c(n)+r(n),n=1,2,…,N
(1)
式中:n为脉冲数索引;s、c和r分别表示目标向量、杂波向量和噪声向量,维数均为N×1。由于海面舰船目标运动速度较慢,可视其为匀速运动,且由于OTHR的距离分辨单元尺寸较大,其在一次CIT内的距离走动可以忽略[22]。因此,目标向量s的第n个数据[23-24]为
s(n)=aexp(j2πfd(n-1)Tr)
(2)

根据Bragg散射理论[25-26],OTHR海杂波频谱可建模为两个关于0 Hz对称的Bragg峰[27-28],称为一阶海杂波,而二阶及更高阶海杂波比一阶海杂波低约10~40 dB,一般可直接用高斯白噪声或正弦信号表示[7]。因此,在不考虑频谱展宽的情况下,海杂波向量的第n个数据为
c(n)=b1exp(j(2πfb(n-1)Tr+φ1(n)))+
b2exp(j(-2πfb(n-1)Tr+φ2(n)))
(3)
式中:b1、b2分别为正负Bragg峰对应的幅度系数;fb为海杂波对应的Bragg频率;φ1(n)、φ2(n)为由电离层不稳定造成的相位扰动项[29-30]。
将式(2)和式(3)代入式(1)得到:
y(n)=aexp(j2πfd(n-1)Tr)+
b1exp(j(2πfb(n-1)Tr+φ1(n)))+
b2exp(j(-2πfb(n-1)Tr+φ2(n)))+
r(n),n=1,2,…,N
(4)
慢时间向量y与频域向量x的对应关系可通过逆傅里叶矩阵A∈CN×N表示:
y=Ax
(5)
式中:矩阵A的第(p,q)个元素为ap,q=exp(j2π(p-1)(q-1)/N),p=1,2,…,N;q=1,2,…,N。由式(4)可知,目标和杂波对应的频率分别为fd和±fb,而噪声相对杂波和目标较弱。因此,频域向量x具有近似稀疏性,非零值集中在频率fd和±fb处。
1.2 非均匀采样回波信号模型

(6)
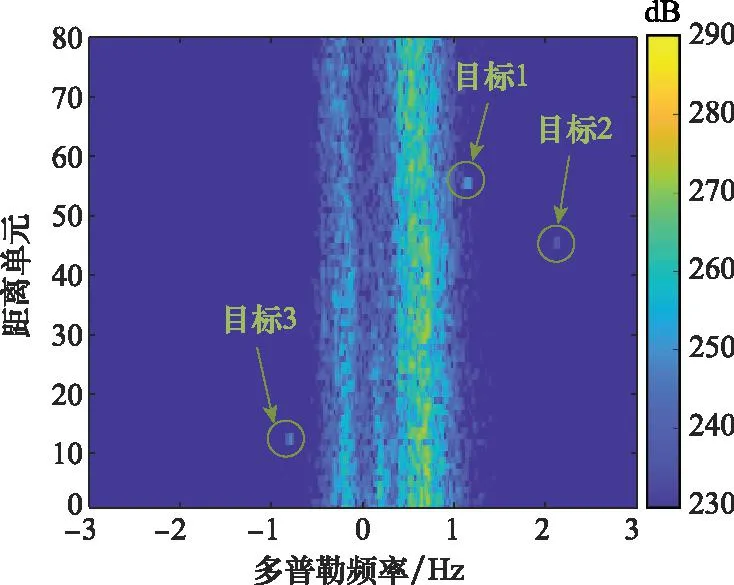
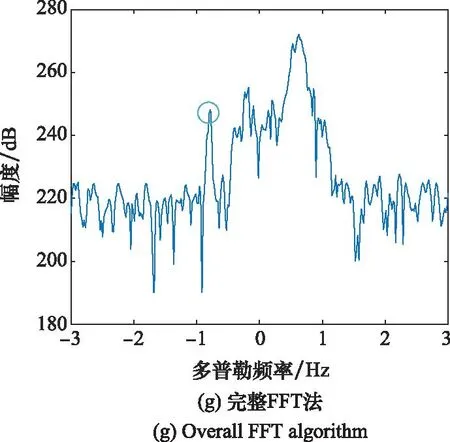
式中:M 图1 感知矩阵构造方式Fig.1 Construction way of sensing matrix 因此,式(5)在非均匀采样条件下可改写为欠定方程组: y′=A′x (7) 式(7)的解有无穷多个,但由于x具有近似稀疏性,式(7)可转换为最小绝对收缩和选择(least absolute shrinkage and selection operator, LASSO)问题,从而通过CS重构算法恢复信号完整频谱[20,31]: (8) 针对式(8),CAMP算法执行迭代如下[20]: (9) (10) (11) 由于杂波背景的复杂性和缺损信号数量的不确定性,最佳阈值参数τ是变化的。文献[19]给出了一种自适应方案,但需要多次执行CAMP算法以选择最佳阈值,运算量较高。此外, LASSO问题导出的复软阈值函数会导致重构精度下降[21]。为解决上述问题,本文提出FACAMP频谱重构算法。 本节对FACAMP算法进行理论分析,首先推导了基于MMSE准则的复降噪函数ηMMSE,并以此代替复软阈值函数;其次,给出了ηMMSE参数的自适应估计方案;最后,给出了FACAMP算法的实现步骤。 文献[33]针对实数信号,将稀疏信号的非零元素建立为伯努利-高斯先验模型[34]: (12) (13) (14) 式中: (15) 2.2.1σ0t的估计 (16) 2.2.2pt的估计 (17) (18) 则错误判决概率为 (19) 将错误判决概率设为α,得到阈值γt: (20) (21) 式中:sum(·)为计数函数;1(·)为指示函数。 2.2.3ut与σ1t的估计 (22) 假设各元素独立同分布,构造似然函数: (23) (24) 至此,给出了所有未知参数的估计。将式(14)改写为 (25) 综上所述,FACAMP频谱重构算法流程归纳为算法1所示。 算法 1 FACAMP频谱重构算法输入 非均匀采样慢时间信号y',感知矩阵A';输出 频谱x的非稀疏估计x~;初始化:x^0=0,z0=y',t=1,tmax=100;步骤 1 更新非稀疏估计x~t=A'Hzt-1+x^t-1;步骤 2 通过式(20)计算阈值γt;步骤 3 分别通过式(16)、式(21)、式(24)计算估计值σ^0t,p^t,σ^1t和μ^t;步骤 4 更新中间变量zt=y'-A'x^t-1+zt-11δ∂η^MMSEt(R)∂x(R)(x~t);步骤 5 更新稀疏估计和迭代次数x^t=η^MMSEt(x~t),t=t+1;步骤 6 迭代终止条件若t>tmax或x^t+1-x^t22/x^t22<10-5终止迭代,否则执行步骤1至步骤5的循环操作。 (26) (27) 至此,本文给出了FACAMP频谱重构算法的实现步骤。下面对比现有算法对实测数据的处理结果,分析FACAMP频谱重构算法的重构性能。 为验证所提算法的有效性,本文采用某OTHR海面回波实测数据进行验证分析。数据的脉冲数量为N=512,在距离维度截取了80个距离单元。通过FFT进行相参积累,得到完整信号的距离多普勒(range Doppler, RD)图,如图2所示。幅度单位已转换为dB,为更好展示实验结果,值域范围设置为230~290 dB,图中包含强海杂波和3个目标,分别标注为目标1、目标2和目标3,目标参数设置如表1所示,其中信噪比表示相参积累后的信噪比,由于目标频率均未设置在网格点上,各目标的相参积累增益不同。 图2 完整回波信号RD图Fig.2 RD diagram of complete echo signal 实验测试包括频谱重构结果、采样信号数量对重构精度的影响、算法复杂度分析和目标检测性能分析4个方面。对比算法分别为补零FFT法、正交匹配追踪(orthogonal matching pursuit, OMP)[15-16]法、自适应复近似消息传递(adaptive complex approximate message passing, ACAMP)[19]法、奇异值阈值算子的鲁棒主成分分析(robust principal component analysis-singular value thresholding, RPCA-SVT)[18]法和非精确增广拉格朗日乘数(inexact augmented Lagrange multiplier, IALM)[9]法,参数设置与原文献保持一致。其中OMP、ACAMP和FACAMP为CS重构算法,RPCA-SVT与IALM为LRMR算法。 分别将降采样率δ设置为0.5和0.78,对应有效采样脉冲个数分别为M=256和M=400,采样方式为随机采样。图3展示了当M=256时,通过各算法重构的RD图,图4为第13个距离单元(目标3)的频谱。图5展示了当M=400时,通过各算法重构的RD图,图6为第46个距离单元(目标2)的频谱。对重构的目标所在位置进行了标注。 图3 RD图重构结果(M=256)Fig.3 RD map reconstruction results (M=256) 图4 频谱重构结果(M=256)Fig.4 Spectrum reconstruction results (M=256) 图5 RD图重构结果(M=400)Fig.5 RD map reconstruction results (M=400) 图6 频谱重构结果(M=400)Fig.6 Spectrum reconstruction results (M=400) 从图3、图4可知:当M=256时,OMP、ACAMP、FACAMP能够较好地实现频谱重构,补零FFT、RPCA-SVT和IALM的重构性能欠佳。其中OMP重构信号是不连续的,因为背景中包含许多零值,而ACAMP和FACAMP则能够较好地同时实现目标、海杂波与噪声的重构。 从图5、图6可知:当M=400时,除补零FFT外的所有算法均能实现信号与海杂波的重构。其中RPCA-SVT重构的RD图含有较多的虚假重构点,IALM、ACAMP与FACAMP的重构效果相对较好,与原信号频谱最为接近。此外,根据近似消息传递的状态演化分析[32],FACAMP重构的噪声信号与原信号一样,均服从零均值高斯分布。 图7 NMSE与采样脉冲数曲线Fig.7 NMSE versus sampling pulse number curve 从图7可知,基于CS的OMP、ACAMP和FACAMP在采样脉冲数少于384时,NMSE低于RPCA-SVT和IALM算法,FACAMP相对于ACAMP的NMSE降低了约2~3 dB。随着采样数的增加,RPCA-SVT和IALM的NMSE不断降低,其中IALM在采样脉冲数高于400时,NMSE最低。因此,可以得出以下结论:在低采样数条件下,CS重构算法的重构精度高于LRMR重构算法;在高采样数条件下,RPCA-SVT和IALM的重构精度更高;在CS重构算法中,FACAMP的重构精度始终高于OMP和ACAMP。 图8 FACAMP收敛曲线Fig.8 FACAMP convergence curve 因此,上述算法总复杂度由高到低的排序为:IALM>RPCA-SVT>ACAMP>OMP>FACAMP。 算法复杂度可以通过运算时间表征。在采用Intel八核处理器和内存为16G的计算机上,利用上述实验数据,采用仿真软件对5种算法进行RD谱重构,分别设置不同的采样脉冲数,得到运算时间曲线,如图9所示。通过图9可知,运算时间随采样脉冲数的变化并不明显,其中FACAMP的运算时间约为1 s,OMP的运算时间约为10~20 s,ACAMP的运算时间约为30 s。RPCA-SVT的运算时间约为400~700 s,而IALM的运算时间达到2 000 s以上。FACAMP的运算时间明显少于其他算法,与理论分析结果保持一致。 图9 运算时间曲线Fig.9 Running time curve 综上所述,将各算法的重构性能归纳于表2,运算时间和NMSE均为对本文的RD图进行重构而得到的数据。 表2 算法重构性能比较Table 2 Algorithm reconstruction performance’s comparison 本节通过绘制检测性能曲线,进一步验证算法对目标的重构性能。根据CAMP算法的状态演化分析,其具有保持背景噪声高斯性的独特优势[20],且由于多普勒域存在强海杂波的干扰,使用距离维单元平均恒虚警处理(cell average-CFAR, CA-CFAR)得到目标的检测性能曲线。设置虚警概率为Pf=10-3,检测阈值通过106次蒙特卡罗仿真计算得到,信噪比(signal-to-noise ratio, SNR)范围设置为0~26 dB,其定义为SNR=10lg(Ps/Pn),其中Ps和Pn分别表示信号功率和噪声功率。将参考单元和保护单元的数量分别设置为24和4,通过在2 000组实测数据中注入目标以计算检测概率。图10为采样脉冲数分别为256、320、384时FACAMP和补零FFT的检测性能曲线,以及完整采样条件下FFT的检测性能曲线。 图10 检测性能曲线Fig.10 Detection performance curve 从图10可知,当采样脉冲数分别为256、320、384时,由补零FFT导致的频谱失真现象会使目标覆盖于噪声背景中。当SNR为0~26 dB时,几乎无法检测到目标。而FACAMP有效解决了频谱失真问题,使目标的检测性能有了很大的提升,且随着采样脉冲数的增加,目标的检测性能不断提升。 本文针对OTHR非均匀采样的频谱重构问题,提出了一种FACAMP频谱重构算法,算法具有重构精度高、运算速度快、自适应性强和可保留背景噪声高斯性的优点。与低秩矩阵恢复算法相比,所提算法在低采样脉冲数下具有更高的重构精度,且运算复杂度显著降低;与CS重构算法相比,所提算法运算速度和重构精度均有一定提升,且能够与现有CFAR处理方案结合。由于在实际应用中,采样数量是已知的,在下一步工作中,可以通过自适应选择频谱重构算法实现最高的重构精度,同时需综合考虑运算时间的成本,选择最佳频谱重构方案。
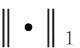
1.3 CAMP算法


2 FACAMP频谱重构算法
2.1 构造复降噪函数



2.2 参数估计







2.3 FACAMP频谱重构算法实现步骤



3 实验与分析
3.1 频谱重构结果









3.2 采样信号数量对重构精度的影响


3.3 算法复杂度分析




3.4 目标检测性能分析

4 结束语

