复杂建设环境下基于Hybrid A*算法的铁路平面线形绿色优化设计

张天龙 何 庆 高 岩 高天赐 李子涵

（西南交通大学，成都 610031）

铁路选线是一个复杂的系统工程，决定工程项目的投资成本、难易程度和安全风险等因素［1］。针对铁路和公路线形优化问题，近年来国内外学者开展了大量的研究工作，引入了多种算法，包括：梯度投影法［2］、遗传算法［3］、动态规划算法［4］、粒子群算法［5］、线性规划算法［6］等。以上绝大部分算法需预先给定控制点的个数以及初始分布情况，随后以平面交点的位置、曲线半径等作为变量，以满足约束条件下的建设成本最小为优化目标，开展逐步优化。值得注意的是，线路的控制点的初始分布对于最终优化结果有着重要影响，设置合理的初始控制点对于设计人员的设计经验有着较高要求。对于复杂环境条件下的设计问题，人工往往难以给出合理的初始控制点分布，使得最终优化结果不理想。针对上述问题，学者们开始尝试引入不需要设置初始控制点的先进算法，包括双向距离变换法［7］、深度强化学习算法［8］、离散网格算法［9］等。然而，以上算法基本采用的是圆曲线-直线协同优化，考虑到模型的复杂性，难以在算法中引入缓和曲线，从而进行符合实际线形规范的几何协同优化。

此外，随着近年来“绿色铁路”概念的提出，在原有的复杂优化问题下，引入“绿色”“低碳”等因素并提出了新的要求。本文提出了一种基于改进自动驾驶汽车导航算法的顺序探索算法——Hybrid A*算 法［10］，能够在未给定初始控制点信息的前提下，考虑铁路线形的实际几何约束，同时将环境生态成本与建设成本融合在内，开展自动化求解拟全局最优的铁路平面设计线形。

1 改进Hybrid A*算法模型

改进Hybrid A*算法流程如图1所示，具体可分为数据准备阶段和迭代优化阶段。

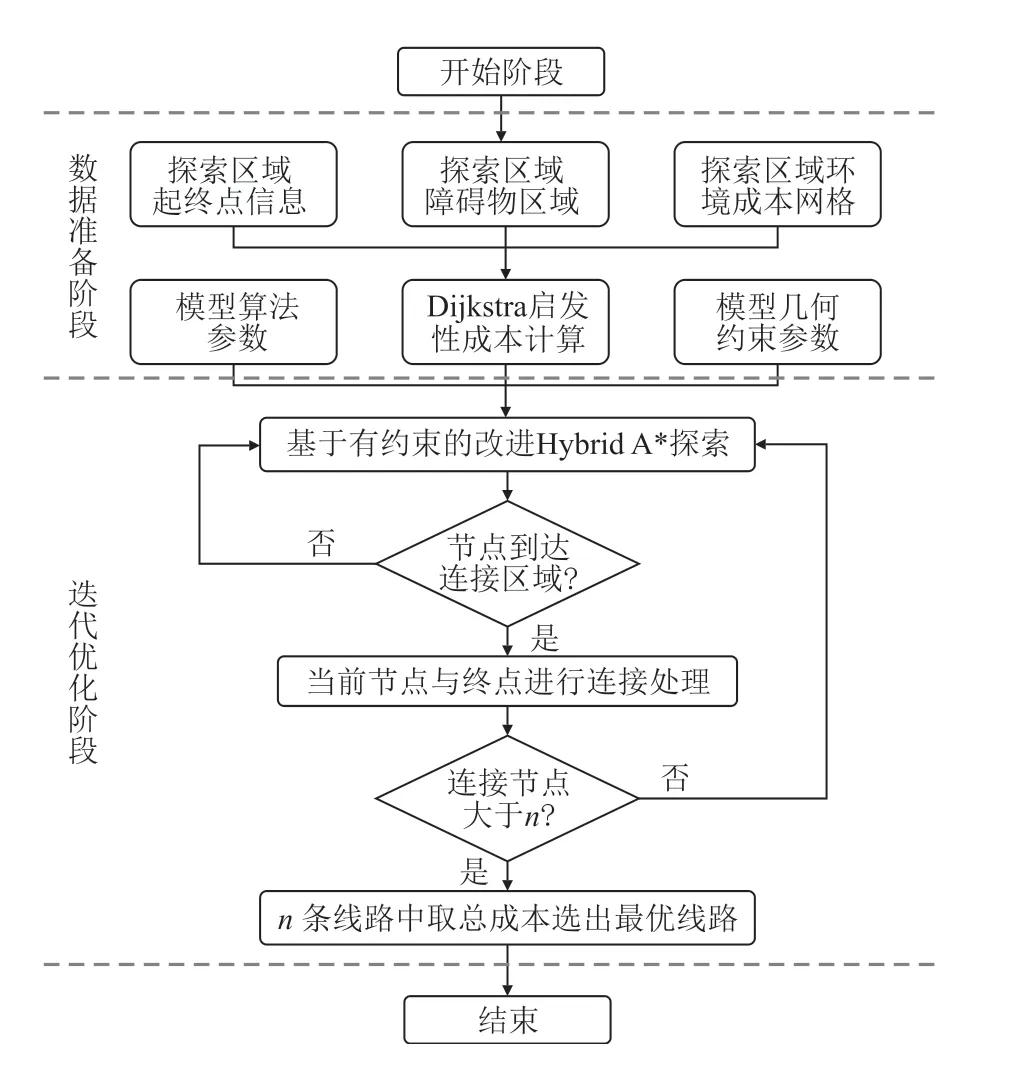
图1 改进Hybrid A*算法实现流程图

1.1 几何参数变量表征

在铁路线形平面优化过程中，常采用的几何变量的参数形式如图2（a）中所示，可用［（xi，yi，Ri，ωi），（xi+1，yi+1，Ri+1，ωi+1），...］来确定一条线路的几何形位。其中每个水平交点包含4个变量：交点横坐标x，纵坐标y，圆曲线半径R以及圆曲线对应的圆心角ω。通过优化各个交点相应的参数，实现最优化目标的效果。本文提出的改进Hybrid A*算法采用的几何变量参数形式如图2（b）所示，用［（xi，yi，θi，Ri，li，Ti），（xi+1，yi+1，θi+1，Ri+1，li+1，Ti+1），…］来确定一条线路的几何形位，其中每个节点上包含6个变量：x，y分别表示节点的横、纵坐标；θ表示该节点处线路方向角；R表示节点对应的圆曲线半径，其中直线段对应的半径为None，缓和曲线半径对应的半径为相接圆的半径；l表示该节点开始到下一节点的长度；T表示线类型，用数字‘1’表征圆曲线，‘0’表征圆曲线，‘-1’表征直-圆缓和曲线，‘-2’表征圆-直缓和曲线。

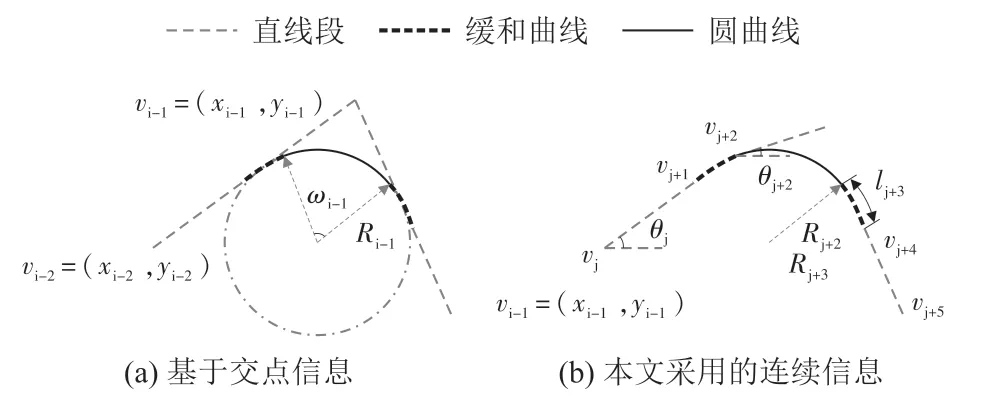
图2 线路几何参数表征方法图

本文采用图2（b）中的表征方法，尽管对应的优化变量相较于图2（a）变多，但其能直接给出里程等信息，并且搜索过程能够从起点逐步过渡到终点，实现渐近式优化。该方法各个节点间的耦合关系相较于图2（a）中更小，更易于优化模型的解耦，提升优化效果。

1.2 模型几何约束与改进Hybrid A*探索

为了保障优化算法的最终精度，往往采用较小的探索步长开展探索工作，较小的探索步长意味着在整个优化空间内考虑更多的线型组合，从中选出的最优组合将具备更好的效果。本文采用的探索方式为定长探索，即除缓和曲线外，直线段和圆曲线都采用相同的单位步长。此外，在改进Hybrid A*算法的探索过程中，还需要考虑线形的几何约束。本文提出的改进Hybrid A*算法中，考虑的几何约束有：最短直线段长度（LSmin）约束，如图3（b）所示；最短圆曲线长度（Lcmin）约束，如图3（e）所示；‘C’形曲线约束，如图3（a）、图3（d）所示；最大曲线半径；最小曲线半径；圆曲线最大偏角（防止回头曲线）。

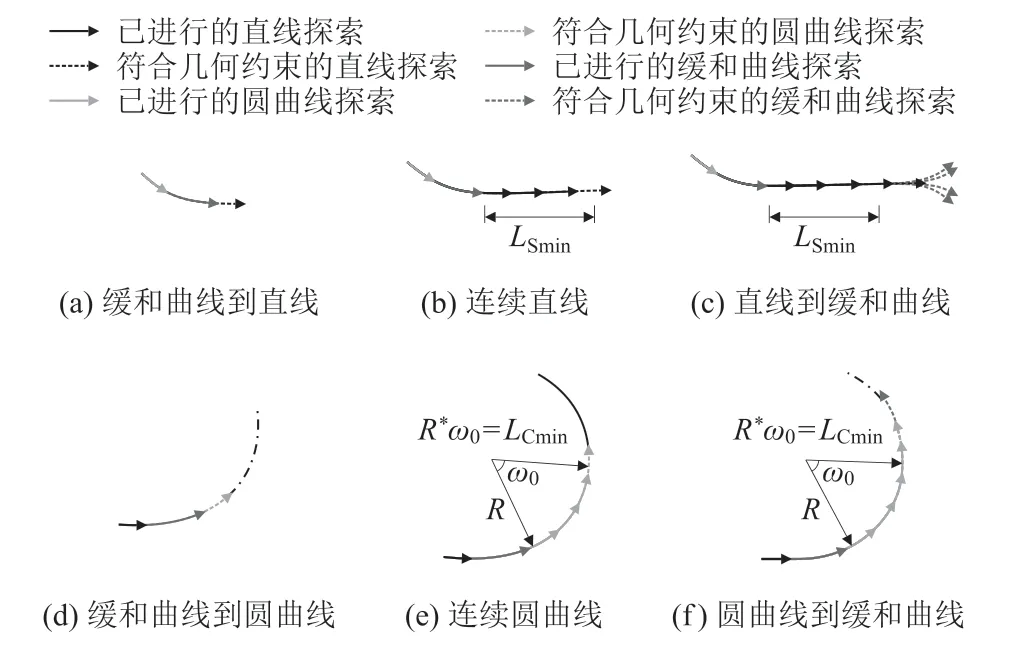
图3 考虑几何约束的Hybrid A*探索图

在满足约束的条件下，可探索的方式为：直线节点的下一个节点可以为直线，也可以为多个方向的定长缓和曲线，缓和曲线对应的相接圆半径R由式（1）确定。圆曲线节点下一个节点可同为圆曲线，也可为缓和曲线，用以向直线段过渡，如图3（f）所示。

式中：Rmin、Rmax——最小曲线半径和最大曲线半径（m）；

1.3 顺序探索流程

原始Hybrid A*算法是基于传统网格顺序探索算法的改进和延伸。网格顺序探索算法基于动态规划的思想，将已探索的区域信息加以存储，在新的探索步骤中将不再考虑已探索过的区域，大幅降低了算法的空间复杂度，使之能够进行整个优化空间的遍历搜索，从中确定接近最优的线路结果。

典型的离散网格探索算法——Dijkstra算法［11］被广泛运用于各领域中。Dijkstra算法顺序探索最短路径的流程如图4所示，该算法从起点出发向四周网格探索，探索过的网格将以列表的形式存储，正在探索的末端节点用树结构存储，树顶为当前总成本最小的探索节点。已探索的区域和正在探索的区域网格存储时，包含当前节点信息和父节点（上个节点）信息。这样一来，一旦探索节点到达终点，便可往前回溯到起点，并且该路径为最优路径。

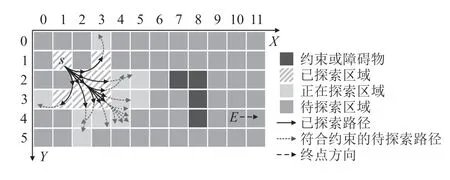
图4 传统离散网格探索流程图

NE——探索方向总数（图3（c）中NE为5）。

原始Hybrid A*算法将离散网格探索算法进行延伸，根据给定的起点坐标和方向，按一定步长进行直线和圆曲线探索，每个探索节点将归入所属的离散网格中，如图5（a）所示。然而，与传统离散网格探索算法的不同之处在于：实际的网格除了平面x，y坐标，还包含节点的角度坐标θ。为了利用动态规划降低模型求解复杂度，并存储已探索的区域，区分未探索的区域，实际采用了两套坐标系统：实际几何连续的坐标系和动态规划离散网格坐标系。前者用于获得实际的线路参数信息，后者用于降低模型复杂度。例如，实际节点坐标为（1.1，2.7，31°），若采用的坐标分辨率为（1，1，5°）进行离散化，记录用于动态规划求解的节点坐标为（1，2，6），已探索过的离散网格节点坐标将不纳入新的探索中。

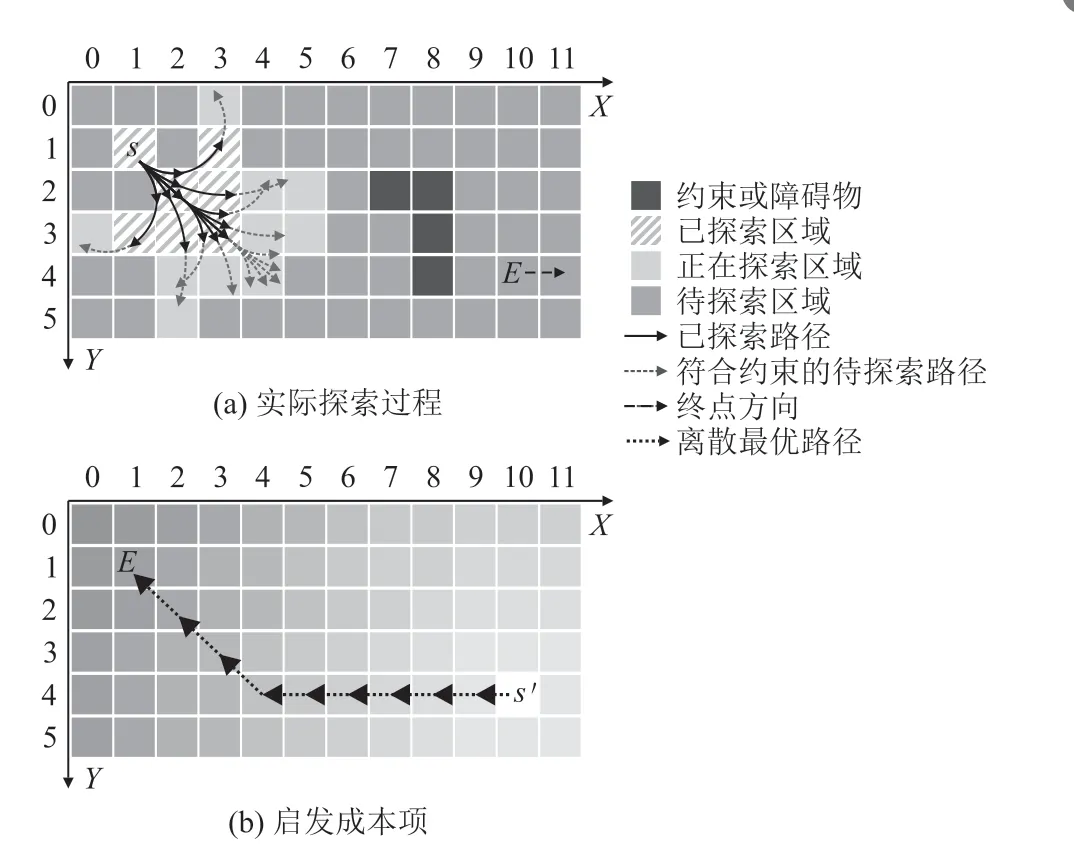
图5 原始Hybrid A*算法网格探索流程图

此外，为了提升探索效率，原始Hybrid A*算法将传统Dijkstra算法作为辅助手段，先利用Dijkstra算法从终点到起点进行一次全局探索，从而获得每个节点到终点的大致距离，并将此作为启发式成本归入算法模型中，如图5（b）所示。其实现方法为在树结构存储正在探索区域时，录入的成本为实际成本与启发式成本的总和，每次选出的最优节点将快速向终点靠近。值得注意的是，启发式成本项在归入模型时，需乘以一个放大系数H-cost。采用改进的Hybrid A*算法时，在上述流程中还需要按1.2小节中的给出的几何约束进行限制性探索。

1.4 最终路径生成与迭代终止条件

在Hybrid A*算法探索过程中，随着顺序探索的进行，探索的节点逐渐向终点方向靠近。考虑到终点处不仅仅包含横纵坐标的约束，同时也具有角度方向的约束，为此，需要一些特殊的手段将已探索的部分与终点进行最后的连接。原始的Hybrid A*算法采用的方式为利用R-S曲线连接已探索的区域和终点，然而，R-S曲线中允许出现反向曲线，符合车辆行驶约束，但与铁路线形设计约束不符。为此，本文提出了一种符合铁路线形设计的连接方法，如图6所示。图中，RL为某一约定半径，表示距离终点一定半径内的区域（连接区域）允许进行终点连接，最先进入连接区域的点为探索区域中最优的节点。连接的方式为：先基于最优节点方向和终点方向，结合半径R确定切点，R的取值与探索时的RE相同，每一个R都需要进行连接计算，判断几何约束并在符合约束的结果中取最优；待切点求得后，依据缓和曲线长度和切点位置重新计算得到新的R'，随即确定整条线路的线型。

图6 Hybrid A*算法终点连接方式图

值得注意的是，尽管最先进入连接区域的是探索区域中的最优节点，但其与终点的连接部分也包含一定的成本，不一定能够保证探索区域中的成本与连接区域中的成本之和是最优结果。为此，本文提出了一种较为简单有效地方式来解决这一问题：将前n个进入连接区域的节点与终点依次进行连接计算，取其中的最优结果作为线路的线型输出，有效地提升了算法的稳定性。

1.5 智能选线模型综合优化目标

上述小节中的提到的原始Hybrid A*算法和改进Hybrid A*算法的优化目标均为路径最短，在平原地区进行铁路平面线形设计中，若考虑线路单位长度造价一致，该优化目标对应于建设成本最低。然而，实际情况下，计算综合成本还需要考虑沿线征地、拆迁和生态破坏等成本，对于一条设定的水平线路（HA），实际综合成本由式（2）确定。在改进Hybrid A*算法中，拓展性地将式中后两项成本通过离散网格方式融入线路成本中，方式与启发式成本的融入方式一致。

式中：TC——综合成本；

CL——线路长度相关的建设成本；

CN——沿线用地相关成本；

CE——沿线生态环境成本。

本文考虑的生态成本指标为归一化植被指数NDVI，为了量化该指标，采用加权的方式简化考虑该成本：即铁路线路每100 m长度的建设成本设为单位1，NDVI相关的生态成本在此基础上进行比例折减，系数为α，如式（3）所示。

2 案例测试

选用的测试案例为华东某地区的卫星影像，影像的尺寸为38.6 km×19.5 km。利用原始卫星影像，经波谱分析得到影像区域范围内的归一化植被指数NDVI，NDVI值越大，表示该处植被越发育。此外，利用卫星影像和其他补充资料，还可以得到该影像区域内各类保护区的位置，铁路线路设计时需要绕避保护区。保护区主要有两类，分别为绿色生态保护区和水资源生态保护区；NDVI图的像素精度为0.1 km× 0.1 km。NDVI的值实际介于-1到1之间，此案例中，为了计算方便，对NDVI值进行了归一化处理，将-1至1归一化到0至1之间。

此案例中，在采用改进Hybrid A*算法求解铁路最优线路时，优化目标只考虑式（2）中的CL和CE，使用的平面几何约束参数有：最小曲线半径4 000 m；最大曲线半径12 000 m；缓和曲线长度200 m；最短圆曲线长度200 m；最短夹直线长度200 m；最大圆曲线偏角180°。使用的算法模型参数有：x，y，θ的分辨率分别为100 m，100 m，0.1°；每个节点向前探索时方向数为20，即对应19组不同的圆半径；启发式成本的放大系数H-cost取0.95；铁路线路每100 m长度的建设成本设为单位1，NDVI相关的生态成本在此基础上进行比例折减，系数为α；在连接区域内取前n=10个最优节点中的最优解作为最终输出结果。将影像左下角的点定义为坐标原点，正东和正北方向分别为x轴和y轴的正向，线路的起点在动态规划离散坐标系内的平面坐标系内坐标为（30，20），角度为0°（正东方向），三维离散坐标为（30，20，0）；线路的终点在动态规划离散坐标系内的平面坐标系内坐标为（370，170），角度为40°（顺时针）。

在不同的α参数下，改进Hybrid A*算法求解得到的最后线路也不同，在α分别等于0，0.01和0.1时求解得到的结果如表1所示，分别对应于图7（a）、图7（b）和图7（c）。由表1可知，改进Hybrid A*算法能够自动控制迭代次数，给出不同数量圆曲线段数的优化线路结果。在α=0.01时，线路总长度为384.51单位，相较于α= 0.1时的392.21单位小，造成此差异的原因之一是不同的α将导致单步探索的成本变化，而优化过程中选取的最优路线是控制总成本最低。由图7可知，改进Hybrid A*选出的路线接近最短路径，与设计目的相符。从表1还可以看出，进行上万次的探索，程序的实际运行时间都在10 s以内。相较于人工选线，大幅提升了计算效率，并且由于人工优化线形难以考虑过多的水平交点个数，优化结果也相较于算法优化效果差。

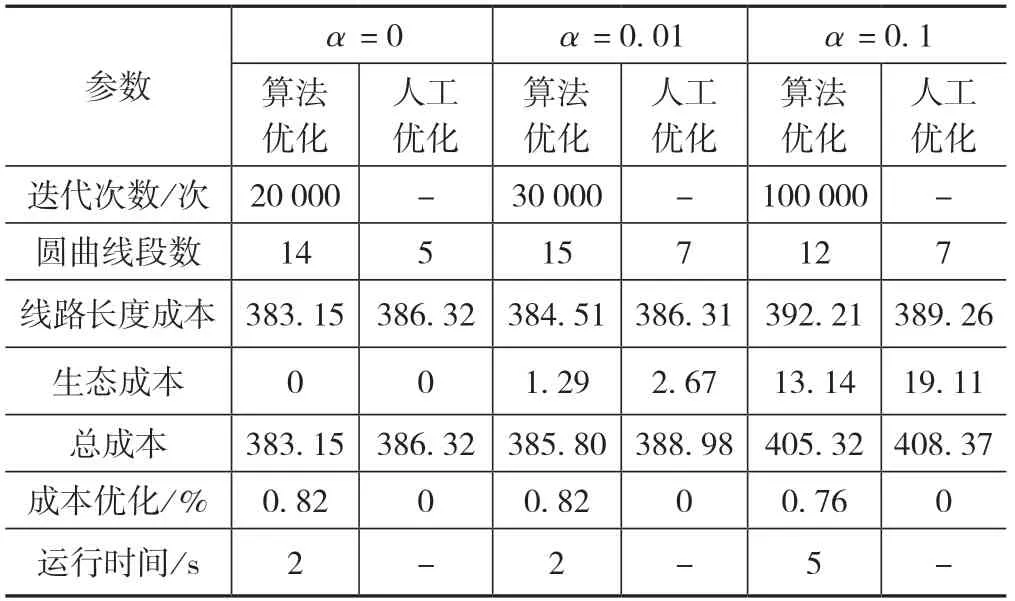
表1 改进Hybrid A*算法求解最优成本线路结果表

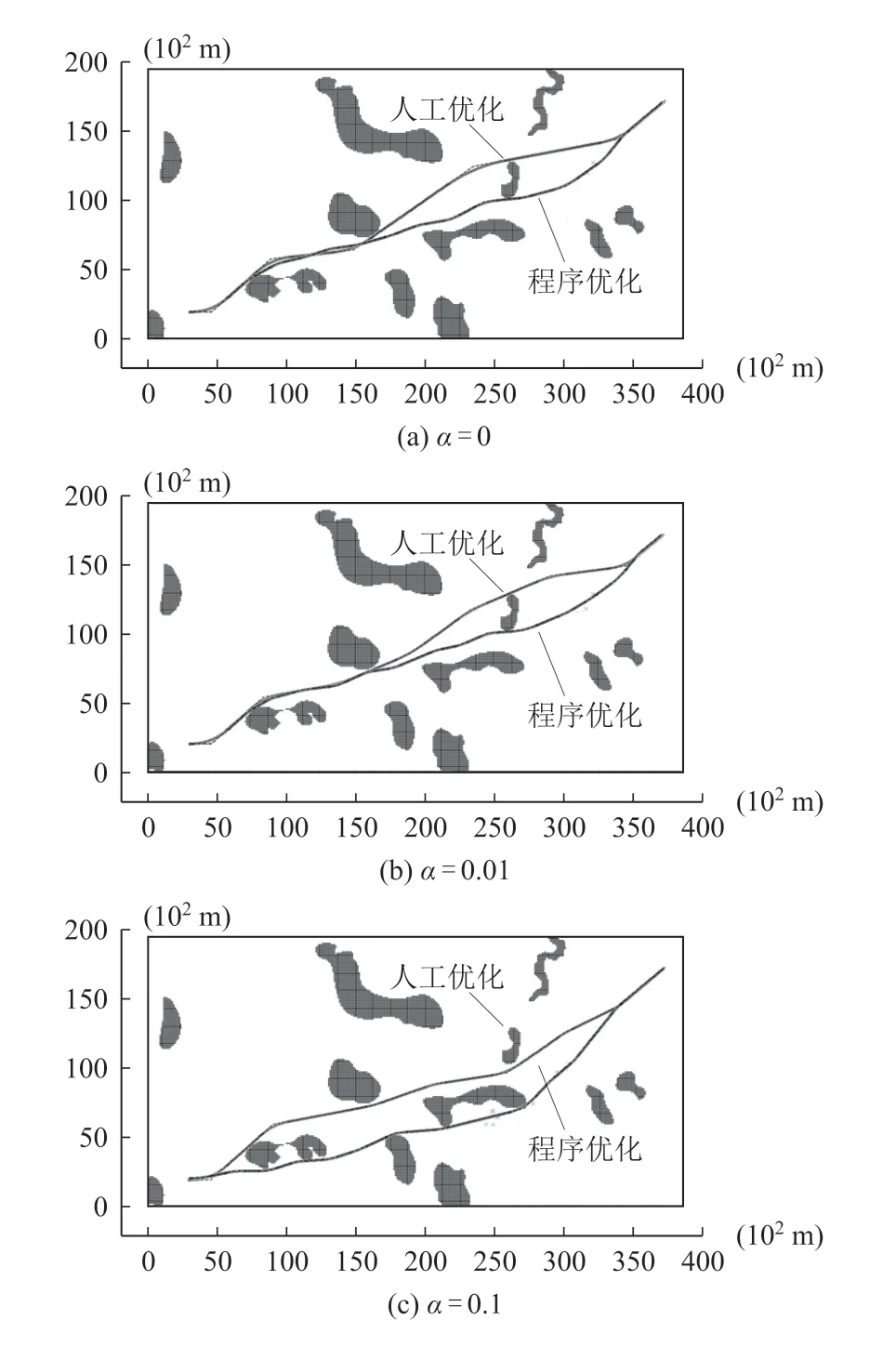
图7 改进Hybrid A*算法求解最优成本线路结果图

3 结束语

本文引入了目前前沿的车辆无人驾驶导航算法Hybrid A*算法，针对铁路选线问题，嵌入了各类几何约束，提出了新的终点连接方法和迭代终止策略，并在算法中融入了离散信息叠加模型。将改进Hybrid A*算法运用到铁路绿色选线案例时，结果表明，相较于人工优化，该方法能够自动、高效地求解出接近全局最低成本、符合几何约束条件的铁路线路，对于指导实际线路设计工作，具有较好的参考价值。

本文将生态环境指标通过加权的形式融合在建设成本中，采用的是单目标优化模型。在将来的研究中，需要引入多目标优化理论进一步提升模型的优化能力。此外，本文仅考虑了铁路线路的平面优化。对于复杂山区的铁路线路优化问题，还需要进一步将算法拓展到三维。