基于改进的频率选择表面结构的性能分析与优化设计

丛 滨,孟 凯,宋伟健

(1.解放军92941部队,辽宁 葫芦岛 125001;2.海军航空大学,山东 烟台 264001)

0 引 言

近年来,随着无线通信技术的迅速发展,频率选择表面(FSS)作为一种具有广泛应用前景的二维材料结构,受到了越来越多的关注[1-5]。FSS材料具有对电磁波频率选择的能力,能够实现对特定频段的信号透波或阻挡,因此在无线通信和雷达系统中有着重要的应用[5-7]。

本文旨在设计和分析一种新型的FSS结构,并通过仿真和测试数据来验证其在X波段和Ka波段的频率选择性能[6-7]。首先对传统FSS结构进行改进,在十字形单元的基础上引入了多边形环状单元,并通过参数优化得到了最佳设计方案。改进后的FSS结构不仅具有更广的通带透波特性,还能够提高入射角稳定性。

为了验证所提出的FSS结构的电磁特性,研究中采用了层叠设计和单层结构2种方案进行比较。通过对比仿真结果和测试数据,可以得出结论：层叠设计的FSS结构在频率选择性能上优于单层结构。这一发现在一定程度上拓宽了FSS的应用领域,为无线通信和雷达系统的性能提升提供了新的思路。

1 频率选择表面设计

频率选择表面通常是一种二维周期金属阵列结构,由大量无源谐振单元周期性排列构成。FSS对电磁波照射的响应类似于一个空间滤波器,对不同频率的电磁波可以具有传输和截止的作用,FSS结构传输/反射频率响应特性曲线示意图如图1所示。比如在某一特定频率下,电磁波入射时会发生明显的谐振现象,使得该频段的电磁波全反射或全透射,谐振频率可根据需求设计。FSS结构工作原理图如图2所示。

图1 FSS结构传输/反射频率响应特性曲线示意图

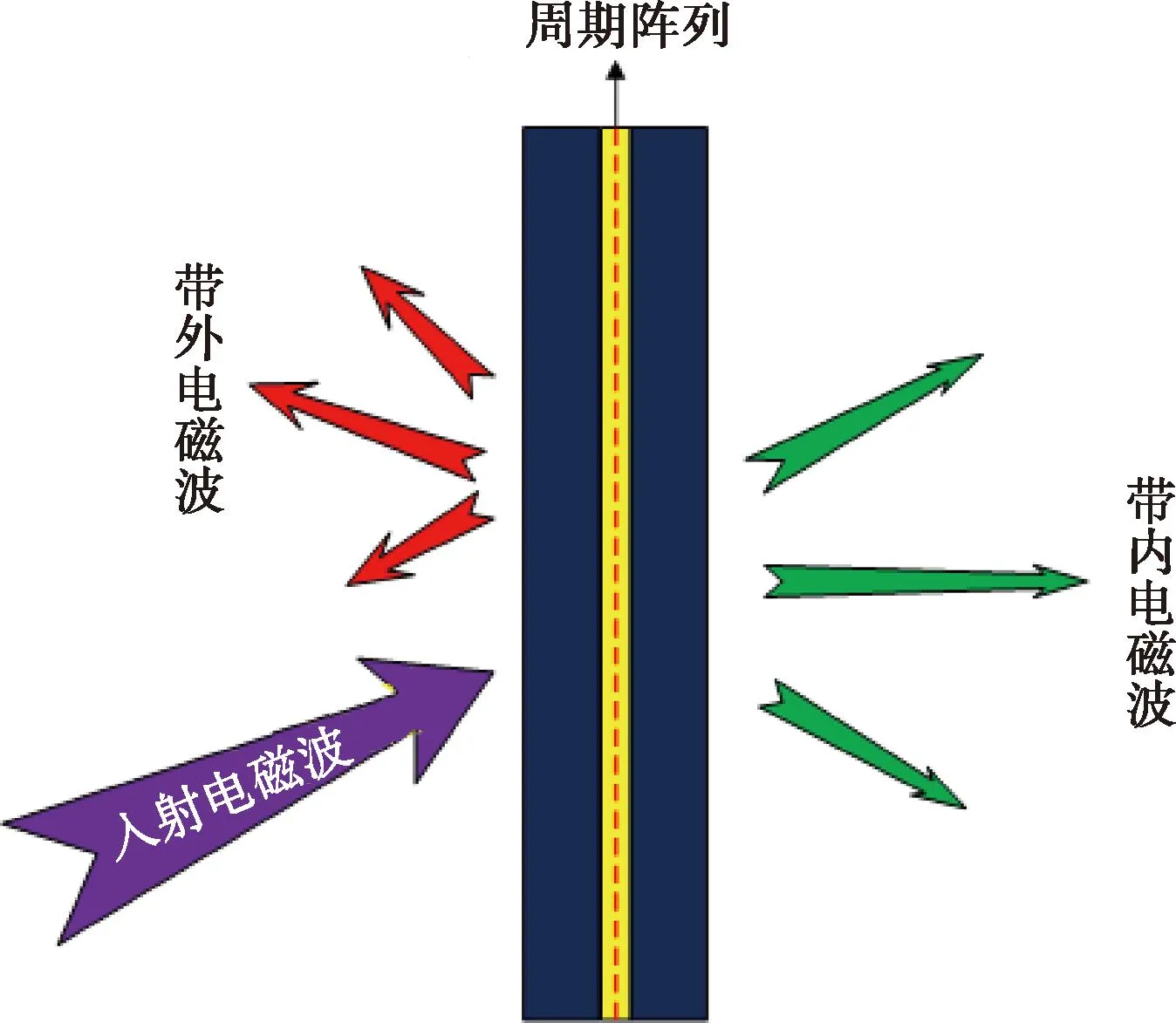
图2 FSS结构工作原理图

根据角反射器功能需求,开展FSS平板设计工作。针对双频段雷达截面积(RCS)需求,确定以X波段带通型FSS作为实现途径。总体设计方案如图3所示。

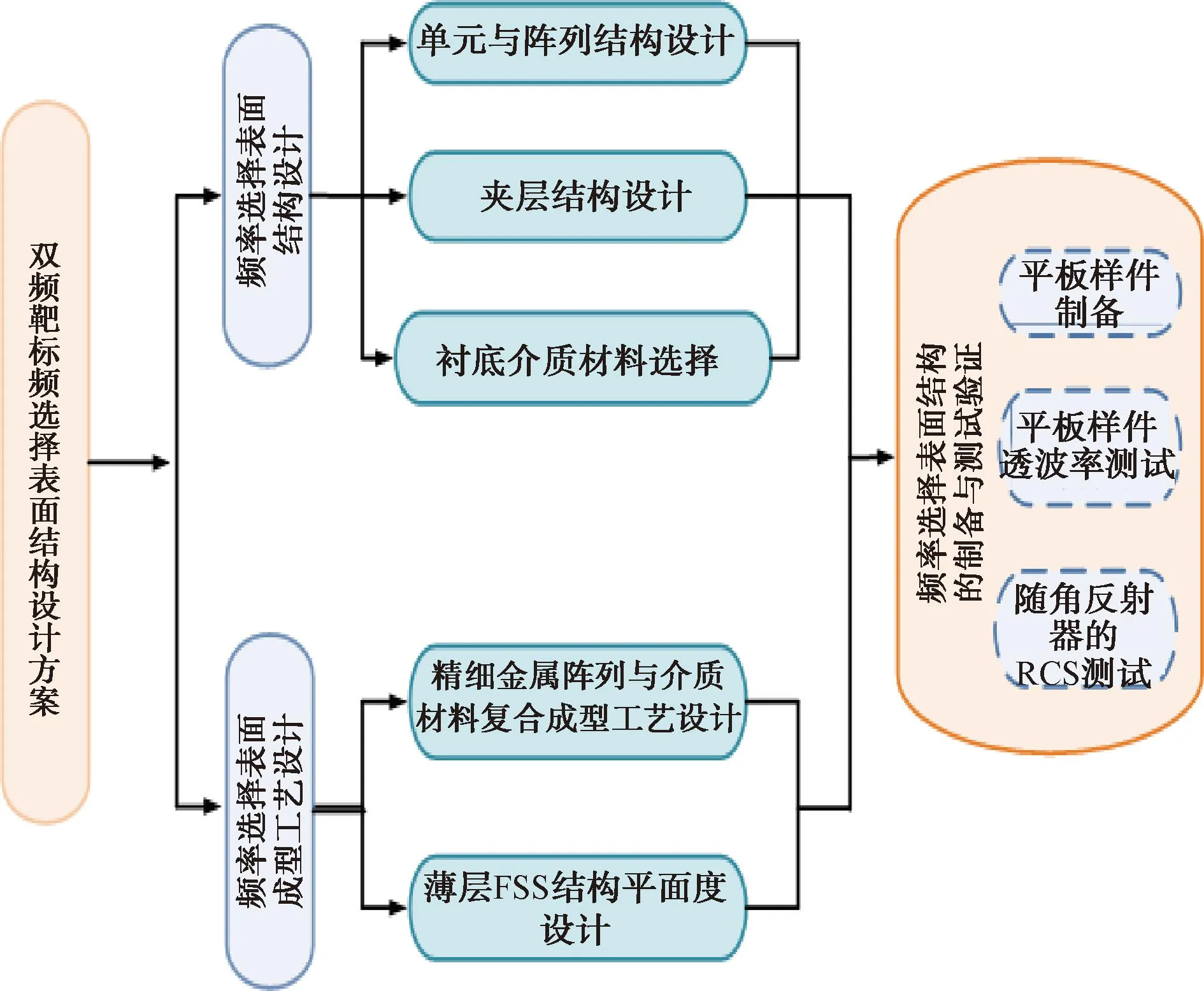
图3 频率选择表面设计流程

首先开展频率选择表面的结构设计,从单元阵列、夹层结构与衬底介质3个方面对FSS的结构进行优化设计,通过仿真与测试最终确定结构形式与参数。其次,开展频率选择表面成型工艺设计,针对已设计完成的FSS结构,根据其层结构特性以及介质材料特性,设计合适的成型方法及工序,加工成型后再针对平板脱模曲度进行平面度优化设计。最终完成平板样件的制备及相关试验验证工作。

2 FSS结构电性能分析方法

等效电路法是用准静态近似的方法来推导FSS结构的等效电路模型,将电磁波在无限大周期阵列上的相互作用看作是电磁波通过一条传输线,用分流集总阻抗来代表阵列,即将FSS结构表示为等效电路的方法;自由空间的特性阻抗为377 Ω,通过解传输线方程得到FSS的反射和传输系数。

2.1 周期排列金属栅的等效电路模型

容性条带：由厚度为0的无限长金属条带构成的无限延伸的平面栅栏,金属条带的边与磁场方向平行。如图4所示,平面波由自由空间中以角度θ入射。

图4 容性条带及其等效电路示意图

在参考平面T处的等效电路参数：

(1)

限制：这样的等效电路仅适用于波长与入射角在如下范围内的情况：a(1+sinθ)/λ<1。对于θ=0°的情况,下面给出更加精确的表示：

(2)

(3)

(4)

感性条带：由厚度为0的无限长金属条带构成的无限延伸的平面栅栏,金属条带的边与电场方向平行。如图5所示,平面波由自由空间中以角度θ入射。

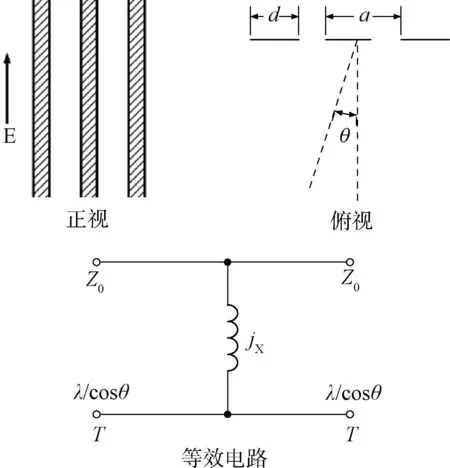
图5 感性条带及其等效电路示意图

在参考平面T处的等效电路参数为：

(5)

这样的等效电路仅适用于波长与入射角在如下范围内的情况：a(1+sinθ)/λ<1。对于θ=0°的情况,在下面中给出更加精确的表示：

(6)

(7)

(8)

2.2 方环单元的等效电路模型

图6为方形环金属单元及其等效电路模型。其等效电路模型为级联的感抗与容抗,其中感抗是由将与电场方向平行的2条边进行等效得到,而容抗是由与电场方向垂直的相邻单元之间的间隔进行等效得到。这里,假设方形环单元的参数分别为：周期为p,2个单元间隙为g,金属贴片宽度为w,单元外侧长度为d。那么可以得到其等效电路中的容抗值。

图6 方环形金属贴片单元及其等效电路

方环单元的归一化感抗为：

(9)

归一化容纳为：

(10)

当FSS阵列两侧附有介质时,根据静电学的有关理论,介质的出现不影响感抗值而对容纳的大小有影响,假设FSS阵列两边加载厚度分别为d1与d2的电介质,其相对介电常数分别为εr1与εr2。此时的等效介电常数εeff如式(11)所示：

(11)

式中：εh=(d1εr1+d2εr2)/(d1+d2);d为电介质的总厚度;D为单元外侧长度。

此时的归一化容抗值为：

(12)

设置各参数如下：周期P=10 mm,线宽W=1 mm,缝隙宽度g=2 mm,方形环外侧单元长度d=8 mm,上层电介质厚度h1=1,下层电介质厚度为h2=2,相对介电常数均为3.2。那么,计算整体结构的反射透射系数时的等效电路图如图7所示。

图7 加载介质FSS等效电路

介质的等效特征阻抗为：

(13)

介质的传播常数为：

(14)

单元阵列的归一化等效阻抗为：

(15)

等效电路的负载阻抗为：

(16)

其中：

(17)

等效电路的输入阻抗为：

(18)

反射系数为：

(19)

传输系数为：

(20)

根据上述推导过程编写Matlab程序,仿真结果与对比结果如图8所示。本文通过计算机仿真技术(CST)进行结构仿真来验证等效电路法的可行性。

图8 方环单元传输特性曲线

如图8所示,2条曲线符合程度较高,证明以上运用等效电路法进行分析所得到的结果是可靠有效的。

2.3 三极子单元的等效电路模型

三极子单元的等效电路模型主要是由十字型单元进行变换而导出,因此首先介绍十字单元的等效电路模型。

如图9所示,十字单元的周期为P,线宽为W,间隔为g,单元长度d=P-g。其等效电路中L1与L2分别代表的是平行于电场方向与垂直于电场的十字臂所带来的感抗,而C1代表的是单元之间的间隔g所带来的容抗,而C2代表的是相邻单元的平行于磁场的十字臂之间的间隔所带来的容抗,等效电路图中各参数可以表示为：

(21)

(22)

三极子单元变换为十字单元后,其等效电路依然如图9所示,三极子单元等效为十字单元的过程如图10所示。

图9 十字单元及其等效电路

图10 三极子单元变换为十字单元

图11 三极子型单元传输特性曲线

这时,等效电路中的各参数表示为：

(23)

(24)

此时FSS层的等效阻抗可以表示为：

(25)

将三极子单元各参数设置如下：P=11 mm,l=5 mm,w=1 mm。通过Matlab程序编程实现等效电路分析,将结果与CST软件的仿真结果进行对比如图11所示。可以看出2条曲线的谐振点重合度极高,验证了等效电路法分析三极子单元的可行性。

3 频率选择表面设计流程

为了获得满足技术指标要求的频率特性,需要适当地设计FSS的周期阵单元的形状、尺寸、排列方式,以及加载介质的电磁参数和厚度,因为这些参数对FSS的频率特性的影响各自独立。对于层叠结构,需要设计的参数将成倍增加。FSS的频率特性还与入射波的入射方向和极化特性有关。当入射波的入射角度、极化特性确定后,考虑主要设计指标有：通带带宽、通带透波率、截止频率。

在FSS结构设计中,为了获得高的截止特性,应尽量避免栅瓣或布拉格瓣的出现。周期阵列单元和常见的阵列相似,为了在大尺寸排列时避免栅瓣的产生,遵循与传统阵列天线相同的抑制栅瓣规则。在垂直入射的情形下,避免栅瓣产生的通常方法是单元尺寸要小于1个波长。对大入射角度,间距要小于自由空间波长的一半。

针对频率选择表面,设计重点为通带透波率设计、入射角稳定度设计以及带外截止特性设计。

频率选择表面中的金属阵列不论从性能设计、结构强度还是实际工况应用方面都必须与介质材料复合成型后应用于实际场景。典型的层结构如图12所示,其中A夹层由2层高密蒙皮和低密度的中间芯层组成,B夹层与A夹层相似,区别在于其两边为低密度介质而中间芯层为高密度材料。C夹层是由2个A夹层结构组合形成的夹层结构,具有强度高、频带宽等特性。

图12 典型的层结构示意图

在层结构设计方面,首先考虑FSS平板在使用中可能需适应风载、浪载、沙蚀、盐雾多种环境,其次从成本控制、厚度与重量等方面出发,在满足各项指标的前提下应选择层数少、重量轻的层设计方案。

单层FSS结构通过系统的参数优化与迭代,其透波率仿真结果如图13所示,可以看出,其当入射角在0～30°范围内,对于水平与垂直2种极化方式,所设计结构的X波段内透波率均在-0.5 dB以上,并且在Ka波段内的损耗基本≥11 dB。

图13 FSS结构两个波段透波率仿真曲线

图14给出了入射角分别为0°、10°、20°、30°时,FSS结构透波率随方位角的变化情况,可以看出所设计频率选择表面的传输特性对于方位向具有较高的角度稳定性。

图14 X波段透波率随方位角的变化情况示意图

图15与图16分别给出了FSS结构在X波段与Ka波段2个典型频点处的电场与磁场的空间分布情况以及远场的散射情况。从图15中可以直观地看出,当入射波的频率为X波段时,FSS所在平面后端的电场与磁场强度明显高于Ka波段电磁波入射的情况。从图16也可以看出,Ka波段电磁波入射时,FSS结构的后向散射明显高于频率为X波段时的情况。

图15 电场磁场分布示意图

图16 后向散射强度示意图

4 结束语

本文研究了频率选择表面的设计和分析方法,设计了具有出色的入射角稳定性和通带透波特性的阵列单元。在FSS结构的层叠设计中,选择了单层结构作为最终方案,具有适应性强、重量轻等优点。最后通过实验验证了设计结构的性能,结果表明其满足设计指标要求,并在X波段和Ka波段的测试数据与仿真结果高度一致。

值得注意的是,本研究不仅关注FSS结构的电磁特性,还涉及到对FSS材料的制备和性能分析。通过详细的实验步骤和结果分析,得出了对FSS结构的制备工艺进行改进的建议,以提高其制备过程的稳定性和可控性。通过对FSS结构的设计和分析,展示了其在无线通信和雷达系统中的潜在优势。通过探索不同的结构和制备方案,为其在实际应用中的推广和优化提供了有力支持。