基于ACO优化的ARIMA-ES-RF布伦特原油价格预测研究

黄 玲, 任苏灵

(兰州财经大学统计与数据科学学院, 兰州 730000)

在全球资源骤减、国际环境局势紧张的背景下,国际原油市场动荡不安,原油作为经济社会中工业发展的“大动脉”,决定工业发展的存亡。据2022年2月17日标准普尔全球普氏能源资讯发布的数据:布伦特原油价格突破100美元/桶,升至100.80美元/桶,是自2014年首次突破100美元/桶的关口以来的第二次突破。随着国际原油价格波动频率加快, 其价格变动具有较大的不确定性。海关总署数据显示,2016年4月,中国原油进口量超过美国,位居全球原油进口榜榜首。原油广泛用于工业生产、航空航天等领域,是保障国家经济和社会安全发展的重要资源。所以石油价格的波动值得人们重视。已有学者研究表明石油价格的波动会导致一个国家的国内经济运行不稳定[1-2]。因此预测原油价格的变化趋势对提前制备政策、稳固国家工业发展、维持经济稳定、社会正常运作具有举足轻重的作用。

基于原油价格在国际社会的重要地位及其时间序列的特征,早期弋小晶[3]使用自回归积分滑动平均(autoregressive integrated moving average,ARIMA)时间序列模型以预测原油价格走势,虽然对于短期序列,ARIMA具有较好的预测性能,但仅靠ARIMA模型难以捕捉长期序列的非线性特征。为提高预测精度,Theerthagiri和Ruby[4]提出了一种基于季节性学习的ARIMA算法,使用加权平均和等精度估计方法以及反馈误差分析来预测布伦特原油价格,预测精度提高了30%到59%。即使目前已有大量方法可改进ARIMA的预测性能,但Mati等[5]研究发现,针对同一序列,时间序列模型ARIMA和时间自回归移动平均模型(TARMA)的预测精度相较于机器学习算法还有待提升。因此,近几年兴起了利用机器学习算法对时间序列的预测研究。Amir等[6]采用了递归神经网络长短期记忆(long short term memory,LSTM)和双向长短时记忆网络(Bi-LSTM)研究了深度神经网络架构,对布伦特原油价格进行了预测,并通过添加层数和更改求解器,对不同误差进行了比较,结果证明具有两层LSTM和随机梯度下降法(SGDM)求解器的模型误差更小,精度更高(均方根误差RMSE为1.53)。Liang等[7]使用深度强化学习算法DRL预测Brent等世界三大原油价格,提出了基于近似优化理论的网络参数动态更新策略,提高了网络的学习效率,证明了深度强化学习算法DRL的普适性。K临近(K-nearest neighbors,KNN)等机器学习算法虽在原油价格预测中也有较好的成效,但是在原油价格以天为单位的高频更新条件下,单一的机器学习算法仍存在一定的局限性,如BP神经网络对超参数和初始权重敏感,极易陷入局部最小值[8]。KNN需要储备所有训练样本,占用内存大,预测速度较慢[8]。为得到更高精度的原价格预测模型,近两年兴起了利用机器学习算法与传统ARIMA模型结合的预测研究。杨李甜和王聪[9]使用支持向量机和GA(遗传算法)改进ARIMA模型;赵兴等[10]利用集合经验模态分解(CEEMD)结合广义自回归条件异方差模型(GARCH)对ARIMA预测残差进行优化,均得到了能规避较大预测误差的组合ARIMA模型。牛东晓和崔曦文[11]利用门循环(gate recurrent unit,GRU)和LSTM结合串行经验模态分解-变分模态分解(CEEMD-VMD)二次分解模型促进了预测结果,得到了更高预测精度的长短时记忆网络-门控循环单元-卷积神经网络-长短时记忆网络(CEEMD-VMD-LSTM-GRU-CNN-LSTM)混合预测模型,在预测精度上有所提升。以上研究结果均表明,通过对比不同模型的预测精度,遗传算法支持向量机-自回归滑动平均模型(GA-SVM-ARIMA)、经验模态分解-支持向量机(EMD-SVMs)等改进的组合模型预测精度远高于单模型。不同于前述研究,Iftikhar等[12]使用Hodrick-Prescott滤波器对原序列进行特殊处理,将原始原油价格时间序列分解为两个新的子序列,建立了预测精度较高的非线性自回归神经网络和自回归移动平均混合模型。

即使不同的组合改进模型在预测精度上有一定提升,但基学习器的组合改进却远不如集成学习能获得更准确和稳健的预测,这是因为基学习器容易造成过拟合。而集成学习在集合以上优点的情况下,通常对噪声和异常值也具有较强的鲁棒性。在多种集成学习中,随机森林(random forest,RF)是Bagging基于决策树而生成的集成学习器。随机森林的最终预测通过平均每棵树的预测得到,可用于处理分类问题,也可用于回归问题,是集成学习算法中最好的算法之一。随机森林算法不容易造成过拟合,在训练时每个基决策树并行训练使得整体的模型训练速度很快。自2001年Breiman[13]提出随机森林算法至今,因为该算法性能优良,被广泛应用于各个领域的分类问题[14-16]和回归问题[17-19],是当下用集成学习算法领域的研究热点。Gupta等[20]利用随机森林和Lasso估计对比分析了石油价格的不确定性对英国失业率变化的作用,研究结果表明石油价格的不确定性可以预测失业率的样本外变化,且随机森林的预测精度更高,即使随机森林的应用广泛。但随机森林在某些噪声较大的分类、回归上仍会出现过拟合。除此之外,还可利用贝叶斯优化[21-22]、进化优化算法[23-25]等来调整模型参数(树的数量、树的根度)或通过调整特征采样比,只保留最重要的特征[26-27]等手段来提高随机森林的训练速度和泛化性能。

2023年国际原油价格中枢回落,市场供需偏紧,地缘政治因素持续扰动[28]。国际原油价格的预测研究对维护我国石油市场的稳定、减轻价格波动带来的财务风险具有举足轻重的作用。ARIMA作为常用于序列预测的方法只能反映序列的线性趋势,无法捕获复杂的非线性关系。指数平滑模型在处理大规模数据的计算速度很快,但不当的参数会直接影响模型的精度。因此,本文提出一种在不损失ARIAM和指数平滑(exponential smoothing,ES)模型的信息下,解决单项模型在长时间序列预测问题上的局限性,提高模型的预测精度和稳健性的ARIMA-ES-RF组合非线性型模型。并在此基础上考虑到随机森林超参数(树的数量、树的深度等)组合的复杂多样性,难以主观确定最适用于原油价格预测的参数,引入具有全局最优性,且用于解决组合优化问题的蚁群算法(ant colony optimization,ACO),优化组合预测模型参数,并用于预测布伦特原油价格。蚁群算法可以根据群体实时信息构建问题解空间,然后通过信息素的实时更新寻找最优解。

1 ARIMA-ES-RF组合模型

1.1 ARIMA模型

自回归移动平均模型(ARIMA)是常被用于时间序列的线性模型[29],ARIMA(p,d,q)一般结构为

(1)

式中:xt、xs分别为平稳时间序列第t期和s期的值;εt、εs分别为与其对应的独立的误差项;σε为误差项的方差;∇d=(1-B)d为d阶差分;Φ(B)=1-φ1B-…-φpBp为平稳可逆ARMA(p,q)模型的自回归系数多项式;Θ(B)=1-θ1B-…-θpBp为平稳可逆ARMA(p,q)模型的移动平均系数多项式。

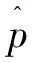
表1 ARIMA模型定阶原则

图1 ARIMA模型建立过程

1.2 指数平滑模型

相较于ARIMA模型只能抓取数据的线性特征,指数平滑模型可融入数据的非线性特征,亦是一种时间序列预测方法,常用于时间序列分析和预测,特别适用于处理平稳或具有一定趋势和季节性的数据,可分为以下几种主要类型。

(1)简单指数平滑模型。适用于没有明显趋势和季节性的时间序列数据。基本模型为

(2)

(3)

下一期的预测值为

(4)

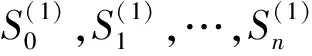
(2)霍尔特线性趋势模型。适用于具有线性趋势但没有季节性的数据。其线性模型表示为

(5)

(6)

(7)

(3)霍尔特-温特斯季节性模型。适用于具有季节性和趋势的时间序列数据。其非线性模型为

(8)

(9)

(10)

(11)

(12)

(13)

1.3 随机森林组合模型

随机森林(RF)是一种强大的集成机器学习方法,常用于回归预测和分类任务,最早由统计学家Breiman[13]于2001年提出。随机森林是树预测器的组合,它使得每棵树取决于独立采样的随机向量的值,并且对于森林中的所有树具有相同的分布。随机森林通过构建多个决策树,并通过集成基决策树的结果来提高模型准确性和稳健性。算法流程如下。

输入:训练数据集D={(x1,y1),(x2,y2),…,(xn,yn)},xi∈X⊆Rn,yi∈Y,Y为输出空间;随机特征数为k;训练轮数为T。

输出:随机森林模型G。

算法过程:①对数据集D自主采样,生成T个样本集;②对T个样本集,生成T个决策树f1,f2,…,fT;③返回随机森林学习器G=g(f1,f2,…,fn)。

图2 随机森林组合模型算法流程

2 基于蚁群算法的ARIMA-ES-RF组合模型参数优化

蚁群算法最早在1992年由意大利计算机科学家Dorigo[30]首次提出。最早的蚁群优化算法是蚂蚁系统,在蚁群优化的仿真中,每只蚂蚁从一个地点移动到另一地点,仿真将信息素留在蚂蚁经过的路径上,但随着时间流逝,信息素逐渐挥发。

蚁群系统是蚂蚁系统的扩展,主要的两个扩展如下。

扩展1: 每只蚂蚁在构造解时会更新局部信息素,一旦蚂蚁从地点i移动到地点j,会沿路更新沿路的信息素:

τij←(1-φ)τij+φτ0

(14)

式中:φ∈[0,1]为局部信息素衰减率;τ0为初始信息素量。式(14)表示当蚂蚁经过地点i和地点j,这段路径上的信息素τij会衰减。若φ=0则τij不变,此时回到最初的蚂蚁系统。在所有蚂蚁都构造了候选解后,实施更新方式

(15)

中的标准全局信息素更新规则。式(15)中ρ为信息素的蒸发率;best表示最优候选解。

扩展2:构造候选解时,使用伪随机比例规则,用(ak→j)表示事件第k只蚂蚁在构造候选解时去地点j。用Pr(ak→j)表示(ak→j)的概率。在构造候选解时,标准蚂蚁系统与蚁群系统的差别如下。

(16)

式中:r随机均匀分布于区间[0,1],可调参数q0∈[0,1]。标准蚂蚁系统用信息素的量推导出概率,蚂蚁k基于这些概率决定去到哪个地点。但在蚁群系统中,蚂蚁k有概率q0去往概率最大的地点,即从当前地点去信息素量最大的地点。

在已建立的ARIMA-ES-RF组合模型的基础上,利用蚁群算法优化随机森林参数。蚁群算法是一种元启发式算法,来源于观察蚂蚁寻找食物的行为。ACO算法模拟了蚂蚁在寻找食物时释放信息素和选择路径的过程,以解决各种组合优化问题。蚁群优化算法寻找全局最优的基本步骤如下。

步骤1:初始化信息素和蚂蚁的位置。在问题空间中,随机放置一定数量的蚂蚁,并初始化路径上的信息素值;

步骤2:蚂蚁选择路径。每只蚂蚁根据一定的概率规则选择下一个要访问的节点。通常,蚂蚁会倾向于选择未访问过的节点。并且信息素浓度较高的节点有更大的概率被选择。

步骤3:蚂蚁移动。蚂蚁按照选择的路径移动,记录所经过的节点和路径的成本。

步骤4:更新信息素。当所有蚂蚁完成移动后,更新路径上的信息素值。信息素的更新包括信息素浓度减少和蚂蚁经过的路径上添加新的信息素,更新公式为

(17)

式中:Lk为第k只蚂蚁的路径长度。

步骤5:重复步骤2～步骤4,设置最大的迭代次数,直至达到预测误差最小的停止条件。

3 实例分析

3.1 数据来源与处理

合理且有意义的预测结果需要建立在大量的历史数据上。为有效预测石油价格走势,选取新浪财经网2022年1月1日至2023年7月30日的布伦特原油每日收盘价格作为研究对象,数据源自一个变量的时间序列,故无须进行标准化处理。针对所得布伦特时间序列中的缺失值,根据原油价格变动的特点,用缺失前一项数据替代缺失值,如缺失项为6月24—25日的油价,6月23日的布伦特油价为74.39,则24日和25日的布伦特油价为74.39。所用的数据分析软件为Visual Studio Code。基于Python3.11.5内核,得到布伦特原油价格的时间序列变化趋势图(图3)。以均方根误差(RMSE)和平均相对误差(RME)作为衡量模型优劣的主要评价标准,当模型RME值不便于计算时选RMSE作为首要评价标准。

图3 布伦特原油每日价格序列图

(18)

(19)

由图3可知,国际布伦特原油价格于2022年初陡增,在较长一段时间内保持着较高的价格水平。很大原因是2022年1月17日国际社会爆发了俄乌冲突,引发了地缘政治紧张局势,这可能导致原油价格出现剧烈波动。国际石油市场参与者通常会对这种不确定性作出反应,导致价格的快速上涨或下跌。此外还可能引发国际社会对能源供应的担忧,因为俄罗斯是世界上最大的石油和天然气出口国之一。对供应的不确定性亦会推高价格。虽然地缘政治风险可能导致投资者对原油市场加大风险溢价,但这种风险溢价通常是短期的。待局势稍微稳定,风险溢价将会减少,表现为图3中2022年7月后布伦特原油价格逐渐降低,后续保持在较为稳定的水平,较为稳定的数据在一定程度上将奠定未来预测结果的稳定性。

3.2 建立ARIMA预测模型

为计算模型拟合精度并与不同模型进行对比,对2022年1月1日至2023年7月30日的数据以8∶2的比例划分训练集和测试集,针对训练集建立ARIMA模型、指数平滑模型,利用测试集检验模型拟合效果。在建立ARIAM模型前,调用Python3.11.4中adfuller()函数对序列进行平稳性检验(表2),发现原序列非平稳,对原数据进行一阶差分处理并绘制自相关图和偏自相关图(图4)确定阶数。

表2 平稳性检验结果

结合表2、图4(a),一阶差分处理后的序列平稳不具有季节效应,根据图4(b)、图4(c)设定不同参数p、q对布伦特原油价格序列的训练集建立ARIMA模型,以测试集作为对照组计算各模型的RMSE确定最优的布伦特原油价格序列的预测模型为ARIMA(1,1,2)。

Var(εt)=4.74

(20)

3.3 建立指数平滑模型

指数平滑模型按平滑的次数可分为简单指数平滑(一次平滑)、霍尔特线性指数平滑(二次平滑)、霍尔特-温特斯季节性指数平滑(三次平滑)。为选择性能最优的指数平滑模型,分别对目标序列训练集建立一次、二次、三次指数平滑,得到不同模型的预测精度指标值(表3)。

表3 不同指数平滑模型预测精度指标值

根据表3最终选择三次指数平滑模型,以RMSE和RME最小为目标在[0.01,0.99]间搜索的最优平滑系数α为0.97,RMSE值为4.77。最终预测结果见表4(表中示例为2023年8月21—31日的数据)。

表4 单项模型2023年8月21—31日预测结果

3.4 建立ARIMA-HW-RF模型并优化

在以上模型结果量纲相同的基础上,结合随机森林模型模拟组合函数中输入、输出特征的量纲无差异的特点,训练随机森林模型时可不对输入特征标准化。

设置随机森林初始参数树的数量为100,树的最大深度为5,最大迭代次数为100。以ARIMA(1,1,2)和三次指数平滑模型在2023年8月1—20日的预测值作为输入特征,实际值为输出特征训练随机森林,对未来11天(8月21—31日)的布伦特原油进行预测(表5)。

表5 组合模型2023年8月21—31日预测结果

基于已经训练好的ARIMA-ES-RF模型,引入进化算法对其参数调优。

第1步:设置随机森林初始参数树的数量为100,树的最大深度为5,树的数量迭代范围为(1,150),最大深度迭代范围(1,20),最大迭代次数为200。

第2步:利用Python中确定性全局优化算法函数dual_annealing来优化随机森林模型的参数。dual_annealing 函数使用了一种双重模拟退火算法,其中参数的搜索过程是通过渐变优化来完成的,而不涉及蚂蚁数量或信息挥发率。因此,在dual_annealing中,不需要设置蚂蚁数量或信息挥发率。

第3步:以最小的RMSE、RME值为终止条件,得到最优的随机森林参数,树的数量为11,最大深度为1。

第4步:以ARIMA(1,1,2)和三次指数平滑模型在2023年8月1—20日的预测值作为输入特征,实际值为输出特征训练随机森林,对未来8月21—31日共11 d的布伦特原油进行预测(表5)。

通过比较表4和表5发现,单项模型都没有组合模型的预测精度高。ARIMA-ES-RF组合模型的平均相对误差RME为1.10%,均方根误差RMSE为1.15;蚁群优化参数后的ARIMA-ES-RFAOC模型的平均相对误差为0.86%,均方根误差RMSE为0.88。蚁群优化参数后的模型RMSE降低了0.27,RME降低了0.24%,说明经过蚁群优化算法优化后的随机森林模型具有很好的可预测性,验证了蚁群优化仿生算法对随机森林超参数优化的可行性、优良性。

4 结论与建议

基于2022年1月至2023年7月的布伦特原油价格数据集,利用集成学习算法随机森林(RF)结合ARIMA模型和ES模型的预测结果,构建了ARIMA-ES-RF非线性组合模型,考虑到随机森林模型中超参数随机组合的复杂性,利用进化遗传算法ACO优化了非线性组合模型ARIMA-ES-RF的超参数。结果表明蚁群优化参数后的ARIMA-ES-RF模型的预测误差显著降低,且明显低于已有文献提出的组合预测模型。

由实验结果可观察到,随机森林算法相比于单一学习器已有较高的精度,但利用遗传算法ACO进行全局优化后的模型精度更高,预测误差更小。通过对国际布伦特原油价格的预测,证实了本文提出的基于ACO算法优化的ARIMA-ES-RF非线性组合模型的可行性和优良性。较低的预测误差意味着本文提出的原油价格预测模型合理有效。

但该模型还有需要继续改进的地方:①单项模型的选择及优化处理;②随机森林的初始参数设定;③蚁群优化算法的算法改进等。未来可尝试进一步优化该组合模型并验证其适用领域。

合理有效的原油价格预测模型可用于支持政府、公司和投资者在能源领域的决策。这些决策可以涉及资源分配、投资战略、政策制定和市场参与等方面。另外,能源公司、金融机构和投资者可以使用原油价格预测模型来管理风险。通过了解未来价格的可能波动,可以采取相应的措施,以减轻价格波动带来的财务风险。再者,原油价格的波动会影响整个供应链,从生产商到消费者。通过合理的价格预测模型,公司可以更好地规划原材料采购、生产计划和定价策略,以确保供应链的稳定性。预测结果表明2023年8月初的布伦特油价大约维持在83美元/桶,今后可收集更多相关历史数据以获得更准确的预测模型。