计数原理单元测试卷（B 卷）答案与提示

一、单选题

1.D 2.B 3.C 4.C

5.A 提示:22个参赛名额分配给20个班级,每班至少1个参赛名额,名额无区别。

可将22 个参赛名额视为22 个球,排成一列形成21个空隙,插入19块隔板分成20份,每一份至少1个球,所以不同的分配方法数为

6.C 提示:把5名学生分成2,2,1三组或3,1,1三组两种情况。

共有90+60=150(种)结果。

7.A 提示:(x-1)6的展开式的通项为

则T4=-20x3,T5=15x2。

从而(3x-2)(x-1)6的展开式中x3的系数为3×15+(-2)×(-20)=85。

①若“电动自行车修理”安排1 名男教师,则余下4人安排到另两个项目,每个项目2人,有C14C24C22种不同的安排方法;

②若“电动自行车修理”安排2 名男教师,则余下3人,1人安排到“绿植修剪”,2人安排到“蔬菜种植”,有C24C13C22种不同的安排方法。

(2)若“糕点制作”安排2 名女教师,则“电动自行车修理”只能安排1名男教师,余下3人,1人安排到“绿植修剪”,2人安排到“蔬菜种植”,有种不同的安排方法。

二、多选题

9.ACD 提示:A,B在后3天介绍的方法种数为A23A44=144,A 正确。

C,D相隔一天介绍的方法种数为,B错误。

E不在第一天,F不在最后一天介绍的方法种数为A55+C14C14A44=504(或A66-2A55+A44=504),C正确。

A在B,C之前介绍的概率为,D 正确。

10.ABD 提示:对于选项A,令x=1,可得2+22+…+2n=a0+a1+a2+…+an-1+an=126,即,2n=64,解得n=6,所以A 正确。

对于选项B,展开式中x6的系数为a6=C66=1。令x=0,可得a0=6。

所以(a0+a1+a2+a3+…+an-1+an)-a0-an=126-6-1=119,B正确。

对于选项C,(1+2x)6的展开式中二项式系数的和为26=64,C不正确。

对于选项D,a0+a1x+a2x2+…+anx6=(1+x)+(1+x)2+…+(1+x)6。

两边求导,可得a1+2a2x+3a3x2+…+6a6x5=1+2(1+x)+…+6(1+x)5。

令x=1,可得a1+2a2+3a3+…+nan=1+2×2+3×22+…+6×25=321,所以D正确。

12.BD 提示:选项A,5个数组成无重复的三位数的个数为A35=60,A 错误。

选项B,奇数为个位数是1,3,5 的三位数,个数为3A24=36,B正确。

选项C,“凸数”分为几类,①十位数为5,则有A24=12(个);②十位数为4,则有A23=6(个);③十位数为3,则有A22=2(个)。

所以共有20个满足题意的数,C错误。

选项D,由选项C的分析可知,D 正确。

三、填空题

13.60 提示:每个路线至少1人,至多2人,则一个路线1人,另外两个路线各2人。

若甲同学单独1人,则有C12C24=12(种)不同的选法;若甲同学与另外一个同学一起,则有C14C12C13A22=48(种)不同的选法。故不同的选择方法有12+48=60(种)。

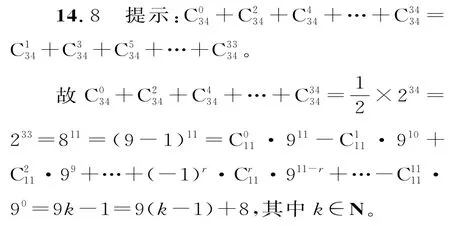
该组合数被9除的余数是8。

15.336 提示:6 个节目全排列的方法数为A66。

6个节目的安排中,歌唱或舞蹈相邻的方法数为2×A22×A55-A22×A22×A44。

所以符合题意的演出顺序数为A66-2×A22×A55+A22×A22×A44=336。

四、解答题

18.(1)令x=1,则展开式中各项系数和为(1+3)n=4n。

由题意知展开式中的二项式系数和为2n。

依题意知4n-2n=992,即(2n)2-2n-992=0,整理得(2n+31)(2n-32)=0。

所以甲不任教“数”的课程安排方案有1 200+240=1 440(种)。

20.(1)无序不均匀分组问题。先选1本有C16种方法,再从余下的5本中选2本有种方法,最后余下3本全选有C33种方法,故共有C16C25C33=60(种)方法。

(2)有序不均匀分组问题。由于甲、乙、丙是不同的3人,在第一问基础上,还应考虑再分配,共有C16C25C33A33=360(种)方法。

(4)在(3)的基础上,还应考虑再分配,共有15A33=90(种)方法。

(5)分成三份,1份4本,另外两份每份1本,这是部分均匀分组问题,求出组合总数除以A22即可,共有(种)方法。

(6)在(5)的基础上,还应考虑再分配,共有15A33=90(种)方法。

22.(1)当组成的数是一位数时,一位偶数有C13=3(个)。

当组成的数是两位数时,可分两类:当末位是0 时,有A15=5(个),当末位是2 或4时,有,两位偶数共有13个。

当组成的数是三位数时,可分两类:当末位是0时,有A25=20(个);当末位是2或4时,有(个)。三位偶数共有52个。

当组成的数是四位数时,可分两类:当末位是0时,有A35=60(个);当末位是2 或4时,有(个)。

四位偶数共有156个。

当组成的数是五位数时,可分两类:当末位是0时,有A45=120(个);当末位是2或4时,有(个)。

五位偶数共有312个。

当组成的数是六位数时,可分两类:末位是0,有A55=120(个);末位是2 或4,有(个)。六位偶数共有312个。

综上,组成的没有重复数字的偶数的个数为3+13+52+156+312+312=848。

(2)万位是1的五位数有A45=120(个),万位是2、千位为0的五位数有A34=24(个)。

万位是2、千位为1、百位为0 的五位数有A23=6(个)。

因此,在21 350 的前面共有154 个数字,21 350是第155个数。