Alignment of Track Oscillations during Tropical Cyclone Rapid Intensification

Tong XIE, Liguang WU, Yecheng FENG, and Jinghua YU

1Key Laboratory of Meteorological Disaster of Ministry of Education, Nanjing University of Information Science and Technology, Nanjing 210044, China

2Dept.of Atmospheric and Oceanic Sciences and Institute of Atmospheric Sciences,Fudan University, Shanghai 200438, China

3CMA-FDU Joint Laboratory of Marine Meteorology, Shanghai 200438, China

ABSTRACT Recent studies on tropical cyclone (TC) intensity change indicate that the development of a vertically aligned TC circulation is a key feature of its rapid intensification (RI), however, understanding how vortex alignment occurs remains a challenging topic in TC intensity change research.Based on the simulation outputs of North Atlantic Hurricane Wilma(2005) and western North Pacific Typhoon Rammasun (2014), vortex track oscillations at different vertical levels and their associated role in vortex alignment are examined to improve our understanding of the vortex alignment during RI of TCs with initial hurricane intensity.It is found that vortex tracks at different vertical levels oscillate consistently in speed and direction during the RI of the two simulated TCs.While the consistent track oscillation reduces the oscillation tilt during RI, the reduction of vortex tilt results mainly from the mean track before RI.It is also found that the vortex tilt is primarily due to the mean vortex track before and after RI.The track oscillations are closely associated with wavenumber-1 vortex Rossby waves that are dominant wavenumber-1 circulations in the TC inner-core region.This study suggests that the dynamics of the wavenumber-1 vortex Rossby waves play an important role in the regulation of the physical processes associated with the track oscillation and vertical alignment of TCs.

Key words: tropical cyclone, rapid intensification, vortex tilt, Rossby wave

1.Introduction

Forecasting tropical cyclone (TC) intensity change still is a major challenge, especially in the presence of vertical wind shear (VWS) within the environmental flow (Huang et al., 2021).Previous studies have found that TC rapid intensification (RI) under moderate VWS is characterized by a vertically aligned TC vortex (e.g., Miyamoto and Nolan, 2018;Ryglicki et al., 2019; Tao and Zhang, 2019; Alvey et al.,2020; Roger et al., 2020; Shi et al., 2020; Shi and Chen,2021, 2023; Schecter, 2022), which can promote a deep secondary circulation by enhancing the symmetric distribution of precipitation and resilience to the ventilation induced by VWS (Riemer et al., 2010; Chen et al., 2018, 2019b; Alland et al., 2021a, b; Fischer et al., 2022).Mostly for an initially weak TC, recent studies have indicated that TC vortex alignment involves the mutual advection of the low-level and mid-level vortices toward one another (Rios-Berrios et al.,2018; Gu et al., 2019; Schecter and Menelaou, 2020;Schecter, 2022).Reasor et al.(2004) and Schecter and Montgomery (2004) attributed the tilt reduction of relatively strong TCs to the damping of vortex Rossby waves (VRWs)through the projection of the tilt asymmetry onto VRWs.So far, the mechanisms responsible for vortex alignment yet to be fully understood.

The motion of TCs often oscillates or wobbles around their mean tracks.Such a track oscillation or wobbling is called trochoidal motion, which has been documented by analysis of radar reflectivity (Jordan and Stowell, 1955; Senn,1961; Jordan, 1966; Hong and Chang, 2005), satellite images (Lawrence and Mayfield, 1977; Muramatsu, 1986),aircraft data (Marks et al., 2008), and numerical simulations(Jones, 1977; Abe, 1987; Liu et al., 1999; Wu and Chen,2016).As noted by Nolan et al.(2001), the time and distance scales of the trochoidal motions in previous observational analyses are in the range of 12-48 h and 20-200 km.In numerical simulations, Yang et al.(2020) and Feng and Wu(2021) found that the tracks of TC vortices at different vertical levels oscillate around a time-averaged mean track.To reach a vertically aligned structure, it is easy to imagine that the TC vortex at each vertical level should oscillate consistently or the oscillation should be substantially reduced in magnitude.Therefore, it is necessary to understand the characteristics of track oscillations associated with the RI process.

Previous studies demonstrated that TC trochoidal motion is a manifestation of TC inner-core dynamics related to azimuthal wavenumber-1 instability (Nolan and Montgomery, 2000; Nolan et al., 2001; Menelaou et al., 2018).By defining the trochoidal motion as the movement of the low-vorticity center relative to the surrounding eyewall structure, Nolan and Montgomery (2000) and Nolan et al.(2001)demonstrated that the wavenumber-1 instability in a hurricane-like vortex can occur due to a local maximum of the angular velocity of the symmetric vortex.For the two-dimensional model of an incompressible vortex on an f-plane, the longtime asymptotic solution consists of a growing discrete mode whose perturbation vorticity is exactly proportional to the basic-state vorticity gradient up to the radius of the maximum angular velocity, a neutral mode representing a displacement of the hurricane-like vortex, and sheared VRWs trapped in the vortex core (Nolan and Montgomery, 2000).The sheared VRWs amplify the discrete mode by producing perturbation vorticity, leading to algebraic instability.In a shallow-water model, Nolan et al.(2001) further indicated that the algebraic instability is replaced by exponential instability while their structures are very similar.They suggested that the wavenumber-1 instability is a triggering mechanism for the persistent, small-amplitude track oscillation in the idealized models.

In this study, we investigate the characteristics of track oscillations of the relatively strong TCs during their RI processes to understand the mechanisms responsible for the vertical alignment of strong TCs.In particular, the following questions are addressed: 1) How do track oscillations of vortices vary with altitude during RI? 2) Do track oscillations contribute to TC vortex alignment? 3) What is the wavenumber-1 structure associated with track oscillations? For this purpose, we will use the simulation outputs of two real TCs.

The remainder of this paper is organized as follows.The two simulation datasets and the selected center-detecting methods and PVT diagnosis are described in sections 2.Sections 3 shows the simulated track oscillation, while sections 4 and 5 discuss the effects of track changes and analyze wave structure, followed by a summary in section 6.

2.Data and methods

2.1.Simulation datasets

Two simulation datasets are used in this study.The first dataset used is from the simulation of Atlantic Hurricane Wilma (2005), which was initialized at 0000 UTC on 18 October and terminated at 0000 UTC on 21 October (Chen et al.,2011).The detailed setup of the Weather Research and Forecast (WRF) model and the corresponding verification can be referred to Chen et al.(2011).The initial and lateral boundary conditions were interpolated from then-operational GFDL model data.There were four interactive domains with horizontal grid spacings of 27 km, 9 km, 3 km, and 1 km, respectively, and 55 levels in the vertical.The model physics options include the Thompson cloud microphysics scheme, the Yonsei University PBL parameterization, and the Rapid Radiative Transfer Model (RRTM) for long waves.

We used the last 54-hour output from the finest-resolution (1 km) domain.Figures 1a and 1b show the simulated and observed tracks and intensities during the 54-h period.As shown in Fig.1b, an 18-h RI occurs from 18 h to 36 h in the Wilma (2005) simulation, followed by a 36-h weakening stage and eyewall replacement as the TC moves into the Gulf of Mexico.Notably, the RI of the Wilma (2005) simulation began with hurricane intensity (Fig.1b).

The second dataset used in this study is from the numerical simulation of Typhoon Rammasun (2014) in the western North Pacific basin (Feng and Wu, 2021).Both the initial and boundary conditions are from the National Centers for Environmental Prediction (NCEP) Final (FNL) Operational Global Analysis data.The four, two-way interactive domains in the longitude and latitude directions contain 251 × 311, 271 × 271, 211 × 211, and 541 × 541 grid points, respectively.The corresponding horizontal resolutions are 18, 6, 2, and 2/3 km (～667 m), with 75 levels in the vertical.The 78-h simulation was initialized at 1800 UTC on 15 July and terminated at 0000 UTC on 19 July.The model physics options include the WRF Single-Moment 3-class microphysics scheme (WSM3) for the outermost domain, the WRF Single-Moment 6-class microphysics scheme (WSM6) for the nested domain, and the RRTM longwave radiation scheme.The large eddy simulation (LES) technique is used for the sub-kilometer domains, while the Yonsei University scheme is used for planetary boundary layer(PBL) parameterization in the other domains.

We used the 48-hour (18-66 h) simulation output from 1200 UTC 16 July to 1200 UTC 18 July from the domain with a horizontal resolution of 0.67 km (～667 m).As shown in Figs.1c, d, the simulated RI occurs during 33-60 h, from 0300 UTC 17 July to 0600 UTC 18 July 2014, as the TC moves over the South China Sea.The simulated azimuthally averaged maximum wind speed is 89 m s-1with a minimum sea-level pressure of 892.5 hPa.Note that the RI process started at the beginning of the selected period for Hurricane Wilma (2005), while it occurred about 15 hours after the selected period for Typhoon Rammasun (2014).The RI period is indicated with shading in Figs.1b, d.The data of the two numerical simulations are vertically interpolated at a resolution of 1 km.

There are two important features in the two simulation cases.First, the two simulations represent two types of RI in the observation.Hurricane Wilma (2005) experienced relatively weak VWS during the 54 hours (Chen et al., 2011).The VWS decreased from about 5 m s-1at the onset of the RI to about 1 m s-1.On the other hand, the RI of Typhoon Rammasun (2014) occurred under moderate VWS, which was about 12 m s-1(Feng and Wu, 2021).Second, the simulated RIs start with initially strong TC intensities, as evidenced by both TCs having reached hurricane intensity prior to the onset of their RIs.

2.2.TC center detection and PVT diagnosis

By evaluating four methods that are often used in TC simulations, Yang et al.(2020) suggested that the minimum pressure variance center (Braun et al., 2006) and the maximum tangential wind center (Marks et al., 1992) can be used in high-resolution simulations of TCs.In this study, we use the minimum pressure variance center because smoother track oscillations and vortex tilt can be obtained.The minimum pressure variance center is detected at each vertical level.

Wu and Wang (2000) proposed using a PV tendency(PVT) diagnosis by taking TCs as positive PV anomalies relative to the environment.A detailed description of the PVT method can be found in the references of Wu and Wang(2000) and Xie et al.(2022).In coordinates that move with a TC, we obtain:

where C is the TC translation velocity, subscripts m and f indicate the moving and fixed reference frames, and the subscript 1 indicates the wavenumber-1 component of the PV tendency.Given the PV tendency in the fixed and moving coordinates and the gradient of the symmetric component of PV,Ccan be calculated using the least square method.The individual contributions of physical processes to PV tendency can be calculated using the following equation:

where ∧1is an operator to obtain the wavenumber-1 component,P,Vhandware potential vorticity, the horizontal and vertical components of the wind velocity, respectively.η and θvare absolute vorticity and virtual potential temperature, respectively.In this study, R is calculated as a residual of (2) and thus also includes the calculation error.When a specific process in Eq.(2) is used to replace the first term on the right-hand side of Eq.(1), we can calculate the contribution of the process in Eq.(2).

In a fixed reference frame, the PV tendency results from the influences of horizontal advection (HA), vertical advection (VA), diabatic heating (DH), sub-grid momentum flux, and friction (FR).The wavenumber-1 asymmetric PV tendency generated in the fixed reference frame plays two roles.One is the movement of the symmetric vortex and the other is the development and propagation of the wavenumber-1 asymmetry (PVTm).The PVT analysis can quantify the contributions of the individual processes (Wu and Wang, 2001).In a high-resolution simulation, Xie et al.(2022) suggested that the PVT diagnosis can be used by increasing the time interval of the model output.The time intervals of the datasets used in this study are 5 minutes for the simulation of Hurricane Wilma (2005) and 10 minutes for the simulation of Typhoon Rammasun (2014).

Compared with those derived from the TC center position, Figs.2 and 3 display the zonal and meridional translation speeds of the two simulated TCs derived from the PVT method at 1 km, 5 km, and 8 km, respectively.We can see that the PVT method can successfully estimate the translational velocities, including the short-time fluctuations.Note that the steering at each level is also plotted in Figs.2 and 3.It is calculated over the same area used in the PVT diagnosis, including the asymmetric inner core.As shown in these figures, the steering is generally different from the vortex movement at the individual altitudes.The success of the PVT method facilitates our analysis of the physical processes related to the simulated track oscillation.

3.The simulated track oscillation

Following Yang et al.(2020) and Feng and Wu (2021),track oscillations for the different vertical levels are obtained by removing the corresponding mean tracks,which are the result of an 8-hour running mean.Examination of the sensitivity to the duration of the averaging window indicates that the resulting track oscillations are very similar to an averaging window ranging from 5-10 hours.For consistency, the same averaging window is also used for all the fields associated with track oscillations.Moreover, a 1-hour running average is used to remove short-time noise.Since the trochoidal motion refers to the track oscillation of the surface center, the track oscillation is used in this study.

Figure 4 shows the resulting track oscillations of Hurricane Wilma (2005) and Typhoon Rammasun (2014) at 1 km, 5 km, and 8 km, representing the track oscillations at the lower, middle, and higher levels.The track oscillations generally exhibit cyclonic rotations around the mean tracks.The large cycles also contain embedded small-amplitude cycles, indicating the different time scales of track oscillations.For Hurricane Wilma (2005), the oscillations are generally similar at different levels due to the weak VWS.During the RI period, as shown in Figs.4a and 4b, the track oscillations at the three levels are nearly identical.After RI, there are small differences in the amplitudes.Typhoon Rammasun(2014) experienced moderate VWS even during the RI period.Although the track oscillations at the different levels are manifested as similar cyclonic rotations (Figs.4e and 4f), the magnitude differences are very clear even 9 hours after the onset of the RI process (Fig.4e).Then the tracks oscillate in a nearly identical way at the three levels(Fig.4f).Figure 4 indicates that the vortex tracks at the different levels oscillate in a nearly identical way during RI.Ryglicki et al.(2018) also found that the tilt experiences smaller-scale wobbles, which are active before RI onset but cease to occur during RI.

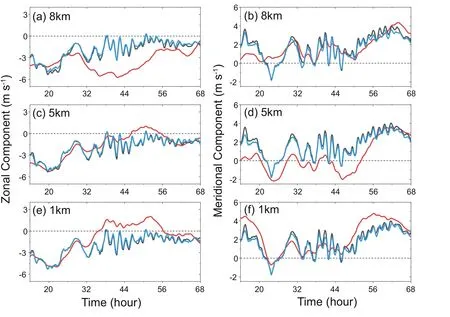
Fig.2.Time series of the (a, c, e) zonal and (b, d, f) meridional translation speeds from the Wilma (2005) simulation as derived from the TC center position (black) and the PV tendency (blue) at (a, b) 1 km, (c, d) 5 km, and (e, f) 8 km after applying a 1-h moving average.The steering flows (red) at the corresponding levels are also plotted.

Fig.3.Same as in Fig.2, but for the simulation of Typhoon Rammasun (2014).

The track oscillations are also evident in the translation velocity.Figure 5 shows the zonal and meridional speeds of track oscillations at the different levels.For Hurricane Wilma (2005), the velocities are nearly identical during the RI period (Figs.5a, c).Their differences in the temporal variations are still small after the RI process.For Typhoon Rammasun (2014) (Figs.5b, d), despite relatively large differences in the early period, the translation velocities are nearly identical at the different levels 9 hours after the onset of the RI process.

The differences in the track oscillations in Fig.4 suggest their possible contribution to the vertical tilt.To quantify the contribution of the track oscillation, we conducted an integration of the tilt between 8 km and 1 km based on the velocities of the track oscillation and the mean track, respectively.The calculated vertical tilt is consistent with that based on the simulated vortex center positions (figure not shown).As shown in Figs.6a and 6b, the vertical tilt in Wilma (2005) is very small due to the weak VWS.After RI, the northwestward tilt is generally less than 2 km in the zonal and meridional directions.In Rammasun (2014) (Figs.6c, d), the vortex tilt is relatively large due to the influence of the moderate VWS.Before RI, the maximum zonal and meridional tilts were about 20 km and 15 km, respectively.About 6 hours before RI, the vertical tilt decreases and a vertically-aligned structure is achieved at 42 h.

As shown in Fig.6, the vortex tilt results mainly from the mean vortex track after RI in Wilma (2005) and before RI in Rammasun (2014), noting further that the track oscillations also make the vertical tilt oscillate.In the simulated Rammasun (2014), the oscillation can lead to a maximum tilt of 10 km in the zonal direction.During RI, the contribution of the track oscillation is comparable to that of the mean track.As can be seen in Figs.6c and 6d their contributions are opposite, leading to a nearly upright structure between 8 km and 1 km.Such opposing contributions can also be seen in the zonal component of the vertical tilt in the Wilma(2005) simulation (Fig.6a).It is indicated that the consistency of the track oscillations in the vertical is important for reaching a vertically aligned TC vortex.

4.Physical processes responsible for track oscillation

To reveal the underlying processes associated with track oscillations, we use the PVT diagnosis method to quantify the contributions of individual processes.As shown in Figs.2 and 3, the PVT method can successfully estimate the TC translational velocity, including the short-time fluctuations in the translation velocities.In this study, the total PV tendency is estimated with the time difference method, and the influence of FR also includes the calculation errors (Xie et al., 2022).

Fig.4.Track oscillations at 1 km (red), 5 km (black), and 8 km (blue) in the Hurricane Wilma (2005) simulation during the periods from (a) 18-30 h, (b) 30-42 h, (c) 42-52 h, and (d) 52-64 h, and for the Typhoon Rammasun(2014) simulation during the period from (e) 22-42 h and (f) 42-62 h.

Figures 7 and 8 show two examples of the influences of the individual physical processes on the track oscillations at 1 km, 5 km, and 8 km in Hurricane Wilma (2005) and Typhoon Rammasun (2014), representing the influences of HA, VA, and DH during (after) the RI of Hurricane Wilma(2005) and before (during) the RI of Typhoon Rammasun(2014).For comparison, the influences of the steering(dashed arrows) are also plotted in the figures.In agreement with Figs.2 and 3, the steering generally cannot account for the oscillation velocity.As shown in Figs.7 and 8, the track oscillation at the individual levels is the result of the combined influences of the physical processes mentioned above, and the influence of FR is generally small except at some moments at 1 km (not shown in the figures).Consistent with Wu and Wang (2001) and Wu and Chen (2016), the direct influence of DH is also important to track oscillations.

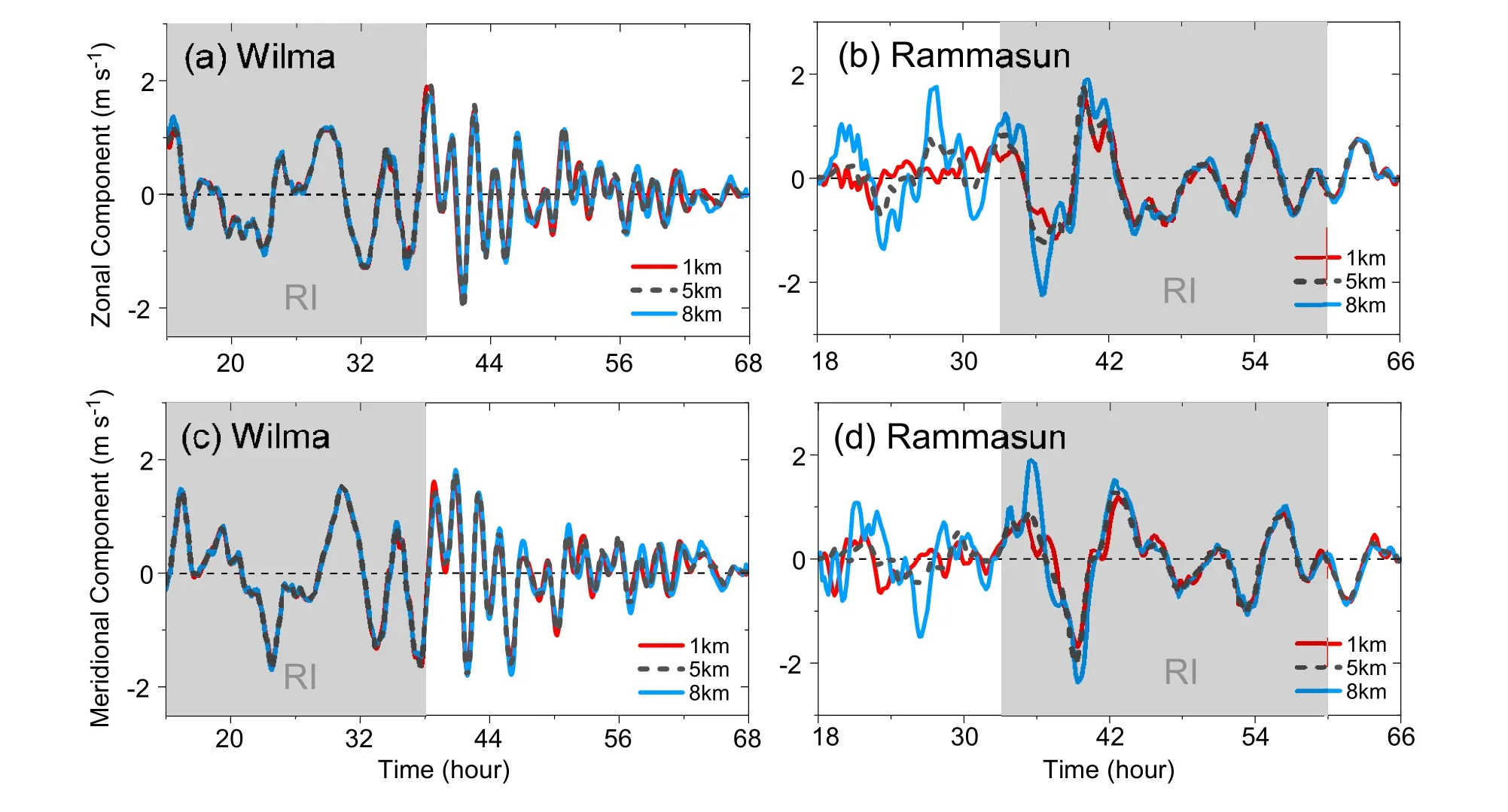
Fig.5.Comparisons of (a, b) zonal and (c, d) meridional speeds of track oscillations based on the TC center position at 1 km (blue), 5 km (black), and 8 km (red) in the Wilma (2005) simulation (left) and Rammasun (2014) simulation(right) after performing a 1-h moving average.The gray shading indicates the RI period.

Fig.6.Contributions of the track oscillation and mean track to the vortex tilt between 8 km and 1 km in the (a, b)Wilma (2005) and (c, d) Typhoon Rammasun (2014) simulations.The black line indicates the total tilt and the blue and red lines indicate the tilt due to the mean track and track oscillation.The gray shading indicates the RI period.

While the total velocities at the different levels are close to one another in magnitude and direction during RI,the influences of individual processes vary significantly at different levels, as shown in Figs.7 and 8.The influences of HA, VA, and DH are not statistically independent.We calculated the correlations between these contributions.For example, the correlations of DH with HA and VA in Rammasun(2014) are -0.44 (-0.60) and -0.76 (-0.60) in the zonal(meridional) direction, respectively.In Wilma (2005), the contribution of VA is significantly correlated with the contributions of HA and DH, with correlation coefficients of -0.63(-0.41) and -0.22 (-0.67) in the zonal (meridional) direction, respectively.In addition, the influence of PVTm suggests the development of a wavenumber-1 circulation although it is generally smaller during RI.The correlations between the above contributions and the presence of the PVTm imply that the track oscillation is regulated by a dynamically coherent structure in the inner core of the TC.

Fig.7.Contributions to the velocity of the track oscillations (black) from HA (blue), VA (green), and DH (red) at (a, b) 8 km, (c, d) 5 km, and (e, f) 1 km at (a, c, e) 23 h 40 min and (b, d, f) 57 h 50 min for the Wilma (2005) simulation.For comparison, PVTm (grey solid) and the steering (black dashed)are also plotted.The black circles represent speeds of 0.8 and 1.6 m s-1 in (a, c, e), and 0.6 and 1.2 m s-1 in (b, d, f).

5.Wavenumber-1 structure associated with track oscillation

Fig.8.Same as in Fig.7, but for the simulation of Typhoon Rammasun (2014) at 23 h 50 min and 51 h 20 min.The black circles represent speeds of 1 and 2 m s-1 in (a, c, e) and 0.6 and 1.2 m s-1 in(b, d, f).

In high-resolution simulations, deep convection and dynamic instability make the inner-core structure complicated.Using the wavenumber-1 component of relative vorticity at 5 km, an empirical orthogonal function (EOF) analysis was conducted to extract the major modes of the wavenumber-1 asymmetric structure associated with the track oscillation during RI because the evolution of the wavenumber-1 asymmetric structure is complicated.In the output of Hurricane Wilma (2005), the analysis period is from 18-28 h.The radius of maximum wind (RMW) at 5 km was relatively stable with an average of 13 km during the period.The analysis area covers a radius of 20 km from the vortex center.In the simulation of Rammasun (2014), the period from 42-60 h is selected for the EOF analysis.During this period, the RMW is about 40 km and the analysis covers an area of 120 km in radius.We also examined the sensitivity to the selected area by extending the analysis area and found that the results are generally not sensitive to the selected area as long as the inner-core region is included.

The first four EOF modes account for 73% and 63% of the variance for Wilma (2005) and Rammasun (2014), respectively.The time series of the first four modes are used to regress the three-dimensional fields of wavenumber-1 asymmetry associated with the track oscillation, and then the regressed fields are used as the asymmetric components to calculate the vortex translation velocity, while the symmetric component is sourced from the simulation outputs.Figures 9 and 10 compare the velocities of the track oscillations based on the regressed fields with those from the original model output at 1 km, 5 km, and 8 km.In both cases, the velocities of the track oscillations can be well retrieved from the regressed fields, indicating that the regressed fields represent the dominant wavenumber-1 asymmetry associated with the track oscillations.Note that no apriori knowledge about the track oscillation is used in the regression.We can conclude that the track oscillations are associated with the dominant wavenumber-1 asymmetry in the TC inner core.

Figures 11 and 12 show the regressed fields of winds, relative vorticity, pressure perturbation, and vertical motion during RI.As mentioned above, these fields are associated with the track oscillations in the simulations of Hurricane Wilma(2005) and Typhoon Rammasun (2014).For comparison,the wavenumber-1 component of the simulated vertical motion (contours) is also shown in the figures.One salient feature is the spiral structure of relative vorticity, consisting of two wavenumber-1 structures generally on the two sides of the radius of maximum PV (RMP).Such a feature is similar to the simulations in the previous studies mentioned in section 1.

For the wavenumber-1 asymmetry outside the RMP,the negative (positive) pressure perturbation is collocated with the cyclonic (anticyclonic) vorticity.The regressed upward motion is generally collocated with cyclonic vorticity.Careful examination indicates that the maximum relative vorticity tilts slightly upwind with increasing altitude.The wavenumber-1 asymmetry inside the RMP is clearer in the Rammasun (2014) simulation.Similar to the counterpart outside of the RMP, the cyclonic (anticyclonic) vorticity is also collocated with the negative (positive) pressure perturbation.

In the inner core of a numerically simulated TC, Wang(2002a, b) found that wavenumber-1 and wavenumber-2 VRWs propagate upwind relative to the azimuthal mean tangential flow around the eyewall.In his simulation, the asymmetric wind fields are quasi-balanced with the geopotential height fields, with cyclonic (anticyclonic) flow collocated with low (high) perturbation geopotential height.In our study, the wavenumber-1 asymmetry in the regressed relative vorticity also propagates upwind relative to the azimuthallyaveraged wind.Therefore, Figs.11 and 12 indicate that the characteristics of the wavenumber-1 symmetry are generally similar to VRWs in Wang (2002a, b).

Fig.9.Comparisons of zonal (left) and meridional (right) speeds of track oscillations (black dashed) derived from the regressed fields with those from the original model output (red) at an altitude of (a, b) 8 km, (c, d) 5 km, and (e, f)1 km during 18-28 h in the Wilma (2005) simulation after applying a 1-h running average.

Fig.10.Same as in Fig.9, but for the Rammasun (2014) simulation.

The two wavenumber-1 VRWs on the two sides of the RMP result from the reversal of the PV gradient.As indicated by the EOF spatial patterns (Figs.13 and 14), the VRWs are radially coupled in an out-of-phase way.In idealized models, Nolan and Montgomery (2000) and Nolan et al.(2001)demonstrated that wavenumber-1 instability occurs as decaying vortex-Rossby waves amplify the growing discrete mode.The coupled waves may be an indication of the influence of the wavenumber-1 instability.The influence declines with time due to nonlinear dynamics and innercore mixing (Nolan et al., 2001).Further examination is required to understand the role of wavenumber-1 instability in the track oscillation of real TCs.Since the track oscillation is controlled by the physical processes discussed in the last section, we may conclude that the dynamics of the wavenumber-1 vortex Rossby waves play a role in the regulation of the physical processes.

6.Summary

Recent studies on TC intensity change have demonstrated that the development of a vertically aligned TC circulation is a key feature of the RI process of TCs (e.g., Chen et al., 2019a; Tao and Zhang, 2019; Alvey et al., 2020;Schecter, 2022); however, understanding how the vortex alignment occurs is still a challenging topic of scientific research.In this study, we used the high-resolution model output from the simulations of Hurricane Wilma (2005) in the North Atlantic basin and Typhoon Rammasun (2014) in the western North Pacific basin to examine the track oscillations at different vertical levels by focusing on the TC vortex alignment during RI.We found that the vortex tracks oscillate consistently at various vertical levels during RI, while the reduction of vortex tilt before RI is mainly the result of the mean track.The vortex tilt results mainly from the mean vortex track before and after RI.During RI, the contribution of the track oscillation is comparable to that of the mean track.

We show that the track oscillations are closely associated with wavenumber-1 vortex Rossby waves that are dominant wavenumber-1 circulations in the TC inner-core region.As indicated by Wang (2002a, b), the wavenumber-1 asymmetry tilts azimuthally upwind with altitude with the negative (positive) pressure perturbation collocated with the cyclonic (anticyclonic) relative vorticity and regressed upward (downward) vertical motion.Consistent with the previous idealized studies (Nolan and Montgomery, 2000; Nolan et al., 2001;Menelaou et al., 2018), track oscillations are closely associated with the wavenumber-1 asymmetry in the inner-core region.Although the track oscillation is determined by the PV tendency, as discussed in section 4, the dynamics of the wavenumber-1 VRWs should play an important role in the regulation of the associated physical processes.

Fig.11.The regressed fields of winds (vector, units: m s-1), vorticity (left, shaded, units: 10-4 s-1), pressure perturbation(left, contour, unit: Pa), and vertical motion (right, shaded, units: m s-1) at (a, b) 8 km, (c, d) 5 km, and (e, f) 1 km at 26 h for Hurricane Wilma (2005).For comparison, the contours in the right panels show the total vertical motion (contour, units:m s-1).The green dashed circle indicates the RMP.The contour intervals are 5 Pa in (a), (b), and (c), and 2 m s-1 in (b), (d),and (f).

Fig.12.Same as Fig.11, but for Typhoon Rammasun (2014).The black dashed circles represent the RMP.The contour intervals are 3 Pa in (a), 10 Pa in (b), 15 Pa in (c), and 0.3 m s-1 in (b), (d), and (f).

In our study, the vortex Rossby wave is the dominant asymmetric mode that is defined relative to the vortex center at each vertical level.While our study agrees with previous studies in that the wavenumber-1 vortex Rossby wave plays an important role in the track oscillation, the definition of the wavenumber-1 asymmetry is different from that of Reasor et al.(2004) and Schecter and Montgomery (2004).In their studies, vortex Rossby waves are the projection of the tilted vortex, which is not necessarily asymmetric relative to the vortex center at each vertical level.However, our study confirms that TC inner-core dynamics play an important role in track oscillation.

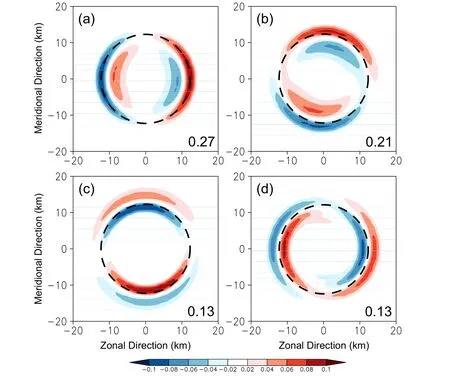
Fig.13.The first four leading modes of the EOF analysis in the simulation of Hurricane Wilma (2005) during its RI.The black dashed circles represent the average radius of maximum PV during the period and the figures are the variance of the individual modes.

Fig.14.The first four leading modes of the EOF analysis in the simulation of Typhoon Rammasun (2014) during its RI.The black dashed circles represent the average radius of maximum PV during the period and the figures depict the variance of the individual modes.

The tilt reduction of TC vortices has been extensively investigated in recent studies.For an initially weak TC, the proposed alignment pathways involve the mutual advection of the low-level and midlevel vortices toward each other(Rios-Berrios et al., 2018; Gu et al., 2019; Schecter and Menelaou, 2020; Schecter, 2022).The roles of divergent and nondivergent flow associated with convective asymmetry have been emphasized in mutual advection.In this study,we show that the tilt reduction of an initially strong TC results mainly from the mean track before RI.Future study is needed to understand how the mean track leads to the tilt reduction.

Data Availability Statement:The underlying research data were the output of a numerical experiment and are available on request by contacting the corresponding author.The data used to create the figures will be available at MyGeoHub and data archiving is underway.

Acknowledgements.We are grateful to Prof.Da-Lin ZHANG of the University of Maryland for providing the model output of the Wilma (2005) simulation and two anonymous reviewers for their constructive comments.The National Natural Science Foundation of China (Grant Nos: 42150710531, 42192551, 61827901)supported this study.