The Contribution of United States Aircraft Reconnaissance Data to the China Meteorological Administration Tropical Cyclone Intensity Data:An Evaluation of Homogeneity

Ming YING and Xiaoqin LU

Shanghai Typhoon Institute, China Meteorological Administration, Shanghai 200030, China

ABSTRACT This paper investigates the homogeneity of United States aircraft reconnaissance data and the impact of these data on the homogeneity of the tropical cyclone (TC) best track data for the seasons 1949-1987 generated by the China Meteorological Administration (CMA).The evaluation of the reconnaissance data shows that the minimum central sea level pressure (MCP) data are relatively homogeneous, whereas the maximum sustained wind (MSW) data show both overestimations and spurious abrupt changes.Statistical comparisons suggest that both the reconnaissance MCP and MSW were well incorporated into the CMA TC best track dataset.Although no spurious abrupt changes were evident in the reconnaissance-related best track MCP data, two spurious changepoints were identified in the remainder of the best-track MCP data.Furthermore, the influence of the reconnaissance MSWs seems to extend to the best track MSWs unrelated to reconnaissance, which might reflect the optimistic confidence in making higher estimates due to the overestimated extreme wind “observations”.In addition, the overestimation of either the reconnaissance MSWs or the best track MSWs was greater during the early decades compared to later decades, which reflects the important influence of reconnaissance data on the CMA TC best track dataset.The wind-pressure relationship (WPR) used in the CMA TC best track dataset is also evaluated and is found to overestimate the MSW, which may lead to inhomogeneity within the dataset between the aircraft reconnaissance era and the satellite era.

Key words: tropical cyclone, intensity, homogeneity, best track, aircraft reconnaissance

1.Introduction

As the most important historical information related to tropical cyclones (TCs), the TC best track dataset is an essential element of both scientific research and operational applications, and this has encouraged many scientists to attempt to improve the quality of data that it contains (e.g., Landsea et al., 2004, 2008; Knaff and Sampson, 2006; Kruk et al.,2010; Hagen et al., 2012; Landsea et al., 2012; Delgado et al., 2018; Emanuel et al., 2018).The best track data are obtained by objective or semi-objective analysis and reasonable estimation based on the analysis (e.g., Jarvinen et al.,1988; Sheets, 1990; Chu et al., 2002; Velden et al., 2006;Ying et al., 2014; Muroi, 2018).The ongoing development of the observational network, techniques, and analysis standards have led to both positive and negative effects; e.g., spurious variabilities have been introduced into the best track data, but errors and biases hidden in the data have been identified (e.g., Landsea et al., 2004, 2006; Song et al., 2010; Wu and Zhao, 2012; Barcikowska et al., 2012; Knapp et al.,2013).Naturally, we wish to improve the dataset to achieve the highest quality possible, but sometimes tradeoffs must be made.Emanuel et al.(2018) summarized two strategies for reanalyzing the TC best track data: one for the best reconstruction of each TC with no attempt at homogeneity, and the other for a more homogeneous dataset with no pursuit of the highest data quality for individual TCs.Regardless of which strategy is selected, a detailed evaluation of the best track data may help to identify spurious variability or hidden errors and biases.

The China Meteorological Administration (CMA) official best track dataset for TCs over the western North Pacific (WNP) basin was initially collated for the seasons 1949-1971 using a reanalysis approach, and, since 1972,has been extended using annual post-season analysis carried out according to the basic rules fixed within the reanalysis project (Ying et al., 2014).It seems likely that the dataset was affected by fewer factitious influences during the early decades, but some common problems may still be hidden within the dataset because of the significant changes in observational networks and technology, such as aircraft reconnaissance over the ocean (Henderson, 1978; Guard et al., 1992;Sheets, 2003; Reade, 2011; Hagen et al., 2012), the weather station network over mainland China (Li et al., 2010, 2012;Ying and Wan, 2011), and developments by the CMA(Hong and Chen, 1983; Wen et al., 2004).

The data obtained from aircraft reconnaissance during the period 1949-1987, flown by the United States Navy and Air Force over the WNP, are particularly important for the CMA TC best track dataset, especially with respect to TC intensity.Approximately 92% of the CMA best track data from this period covered the ocean area over which very few observations were made, but aircraft reconnaissance missions led to nearly 12% of the data from this region being directly observed.However, little information is available regarding how the reconnaissance data were used within the CMA dataset, other than some indirect information found in an operational manual (Operational Department of China Central Meteorological Administration, 1980), which is somewhat of a guideline-like technical summary of the TC best track reanalysis project sponsored by CMA.Problems associated with the aircraft reconnaissance data have also been reported (Shea and Gray, 1973; Jarvinen et al., 1988;Sheets, 2003; Hagen et al., 2012), and little research has been devoted to evaluating the potential influence of these problems on the best track data.Therefore, extensive evaluation of both the reconnaissance data and the CMA best track dataset may increase our understanding of the dataset and improve the data quality.

Problems associated with the TC intensity within the best track data may be more serious than those related to positional data, given the difficulties of observing and estimating intensity.When evaluating TC intensity, the following three issues should be covered: the minimum central sea level pressure (MCP), the 10-m maximum sustained wind speed(MSW), and the wind-pressure relationship (WPR).

1.1.The minimum central pressure

The MCP, as a much more conservative property of a TC than the wind field (Jarvinen et al., 1988), can be obtained via dropsonde or statistical extrapolation from flight-level data (Jordan, 1958; Henderson, 1978;Willoughby et al., 1989).Henderson (1978) suggested that the accuracy of surface pressure measured by dropsonde is within 2 hPa.Hagen et al.(2012) suggested that, because of the absence of wind and position data, the surface pressure observed by dropsonde cannot be assumed to be the MCP,but the observed surface pressure still provides the most important information regarding storm intensity.

Using dropsonde data from TC eyes covering the period 1951-1954, Jordan (1958) proposed the following extrapolation for 500, 700, and 850 hPa:

whereP0the surface pressure (hPa),H5,H7andH8.5are the heights of 500, 700, and 850 hPa levels (m), respectively.The three equations were then used to form a nomogram, with an accuracy within 2 hPa for extrapolation from 700 hPa and lower levels, and within 5 hPa for extrapolation from 500 hPa.The Joint Typhoon Warning Center (JTWC)used the 700-hPa relationship in Eq.(1) in their Annual Typhoon Report 1978 (JTWC, 1978), and reported an accuracy of within ±3 hPa for most TCs.However, Willoughby et al.(1989) pointed out that the hypothetical low-level sounding of Jordan (1958) may not be suitable for TCs with an MCP ＜ 900 hPa and required a correction of +1.6 hPa.

Following Jordan (1958), Liu and Zhao (1978) fitted the extrapolation relationships from 850, 700, and 500 hPa using a piecewise linear regression based on 10 years of aircraft reconnaissance data for the period 1967-1976.They suggested that the extrapolation relationships could be expressed as follows:

These relationships were reported to be more accurate than those presented by Jordan (1958) and were documented as both a cheat sheet and formulas in the CMA’s operational manual (Operational Department of China Central Meteorological Administration, 1980).

1.2.The maximum sustained wind speed

The MSW can be estimated using three approaches.Early on, the MSW could be subjectively estimated only from the sea state (Neumann, 1952) until Doppler Navigation Equipment (DNE) first became available in 1955 and was routinely used beginning in 1957 (JTWC, 1959; Atkinson and Holliday, 1977; Marks et al., 1987; Guard et al., 1992).The estimated MSW, with no distinction made between values recorded from 1500 ft (about 457 m) and those from 700 hPa before the DNE was available (Atkinson and Holliday, 1977), was a major limitation, especially in the case of high winds (Hagen et al., 2012).As suggested by Shinners(cited in Jarvinen et al., 1988), the estimated winds were approximately the same as the anemometer-measured winds for 10.3-15.4 m s-1, but were underestimated by about 3.1 m s-1for 18.5-23.2 m s-1, 6.7 m s-1for 23.7-28.3 m s-1,and 7.7 m s-1for 28.8-33.4 m s-1.

The second approach is to estimate MSW from the flight level maximum wind (FMW) (JTWC, 1959, 1960,1964, 1968).JTWC used an operational nomograph (hereafter the JTWC graph) to estimate the MSW from the FMW, latitude, and flight-level height based on aircraft reconnaissance over the period 1957-1959 (JTWC, 1960), and this was updated using data from 1956-1962 (JTWC, 1963,1964).With a continuous evaluation of the JTWC graph,the estimated wind was found to be overestimated by ～10.3 m s-1.It seems that the estimated wind corresponds much more closely to the maximum gust rather than the sustained wind (JTWC, 1968).Such results, together with a new WPR, were then used to develop a new JTWC graph(JTWC, 1968).

It should be mentioned that the DNE-measured FMW was thought to be accurate to within ±1° in direction and±2.6 m s-1in speed (JTWC, 1959).However, later notes from the JTWC (1964, 1980, 1981) mentioned that the measured flight-level wind may not represent the real FMW because aircraft usually select the weakest part of the TC for penetration and measure the wind only along the flight path.Moreover, the unstable sea surface may introduce large errors in the DNE-measured wind speed because the DNE requires a stationary reference surface to derive the position,and errors in position will in turn affect the wind calculation(Sheets, 2003; Hagen et al., 2012).Further studies also indicated that the DNE-measured wind speed may underestimate the true wind speed by between 5% and 10% in the case of strong wind (Grocott, 1963; Gray, 1967; Shea and Gray,1973).

In terms of the MSW-FMW relationship, the MSW was originally thought to be 15%-25% greater than the 700 hPa FMW (JTWC, 1959).However, Powell and Black(1990) found that the MSW was 55%-85% of the FMW and was strongly dependent on low-level atmospheric stability.In a more recent work, Franklin et al.(2003) examined global positioning system (GPS) dropwindsonde data and recommended that operational factors of 0.90, 0.80, and 0.75 be used to convert the 700, 850, and 925 hPa FMW values to MSW values, respectively.

These previous studies demonstrate that the reconnaissance FMW and MSW were not accurate enough when compared with the pressure data, especially before inertial navigation systems and GPS dropsondes became available (e.g.,Shea and Gray, 1973; Hagen et al., 2012; Klotzbach et al.,2020).For this reason, a third approach was developed to estimate the MSW from the WRP (e.g., Atkinson and Holliday,1977; Harper, 2002; Knaff and Zehr, 2007; Bai et al., 2019),which is discussed in the following subsection.

1.3.Wind-pressure relationship

The WPR is considered a loose physical constraint,such as the gradient wind balance and the cyclostrophic balance (e.g., Holland, 1980; Willoughby, 1990; Willoughby and Rahn, 2004).Most WPRs take the approximate analytical form of the cyclostrophic wind equation (Harper, 2002;Knaff and Zehr, 2007; Holland, 2008):

This equation was fitted based on coastal and island observations in the WNP with a large probability that the TC passed directly over, or just to the left of, the station, ensuring the availability of high-quality data.This WPR, first documented in the Annual Typhoon Report 1974 (JTWC, 1974), is simple and differs from the previous equations used to create the JTWC graph.

Although the AH77 WPR improved upon the previous versions used in the WNP region because it estimated a lower MSW for a given MCP (Harper, 2002), it was still criticized for overestimation (Lubeck and Shewchuk, 1980, hereafter LS80).As explained in LS80, the AH77 WPR used the 50th percentile of gust factors, which may cause an overestimation of 15%-20%, and the inherent uncertainty in converting wind gusts to sustained wind speed may also introduce random errors of nearly 20%.LS80 proposed using the 90th percentile of gust factors and removed the height adjustment for wind observations.These reprocessed data were then used to obtain a new relationship:

As stated in LS80, the values generated using Eq.(7)showed no significant differences to those from Eq.(6).Black (1993) also suggested that the 1-min MSW obtained using the gust factors recommended in LS80 may be more suitable for over-land and coastal winds but a bit low for over-sea winds.This may not be a problem because the stations used in AH77 were either in coastal areas or on islands.Harper (2002) further suggested that AH77 may overestimate MSW by nearly 10%, with one of the principal reasons being the effect caused by the translation speed not being reduced, as AH77 preferred to use wind observations from the right-hand side of TCs.An additional weakness in the regression procedure is the variable accuracy resulting from differing sample sizes among the different intensities,and binning the data before regression was shown to improve the results of the regression analysis (Landsea et al., 2004; Knaff and Zehr, 2007).However, although the data were first sorted by intensity, the binning of the data by the rank of the samples (Knaff and Zehr, 2007) may be affected by the direction of sorting, especially in areas of high intensity with sparse observations, and this acts only to reduce the sample size rather than reducing the unbalanced nature of the sample sizes among different sections of intensity.Therefore, we prefer the binning approach of Landsea et al.(2004).

The WPR developed by Dvorak (1975), which estimates an even greater MSW than AH77 for a given MCP, was also used by the JTWC for satellite-based intensity estimation between 1975 and 1984 (JTWC, 1975-1984).The AH77 WPR was then adopted by Dvorak (1984) for the NWP and used by JTWC (1985).The CMA also continues to use the AH77 WPR for best track analysis, with slight modifications(Ying et al., 2014).Another WPR prosed by Koba et al.(1991) was based on the best track data of the Regional Specialized Meteorological Center (RSMC) Tokyo, and is currently used by that organization (e.g., Muroi, 2018).

Holland (2008) suggested that WPRs with the standard form of Eq.(5) implicitly assume that bothcandnare constants; thus the empirical relationship between wind and pressure, based on regression fitting to observations, constitutes a one-to-one relationship, and can only produce the mathematical expectation of real data.In fact, studies demonstrated that the WPR is affected by parameters such as storm size, latitude, translation speed, and surface roughness (e.g., Landsea et al., 2004; Knaff and Zehr, 2007).Beginning in the early 1960s, the JTWC introduced latitudes into their operational formulas for MSW estimation (e.g., JTWC, 1960, 1963,1964, 1968).Yan and Fan (1994) assessed the influence of latitudes on the parameterscandnin Eq.(5).They found that both parameters are sensitive to latitudes, and the changes associated withnare greater than those associated withc.They fitted the WPR to aircraft reconnaissance data over the WNP for the period 1975-1985 and obtained a set of relationships for the latitudes of 0°-14°N, 15°-24°N, and ≥ 25°N.Their results are similar to Eq.(6) withc=3.4 andnvarying from 0.636 to 0.653.

Holland (1980) developed a parametric profile of axisymmetric wind based on cyclostrophic balance.In his model,the parameter b, which describes the radial width of the wind maximum, is complex (e.g., Willoughby and Rahn,2004), and may depend on ΔP=Pe-MCP, latitude, storm development, and storm translational speed, with storm size excluded due to its unavailability in most best track datasets(Holland, 2008).These factors were also considered by Knaff and Zehr (2007), and the National Centers for Environmental Prediction-National Center for Atmospheric Research (NCEP-NCAR) atmospheric reanalysis and analysis data were used to estimate the storm size and environmental sea level pressure.However, atmospheric reanalysis datasets were found to have major limitations with respect to reproducing the intensity (especially for weak storms)and the MSW radius (Schenkel and Hart, 2012; Murakami,2014; Zick and Matyas, 2015; Hodges et al., 2017).Therefore, it is necessary to evaluate whether it is beneficial to introduce a parameter with associated uncertainty to improve the WPR.

In summary, previous studies have indicated that the aircraft reconnaissance MCP is more accurate than both the FMW and MSW; consequently, the WPR, based on a loose physical constraint, is the best approach for estimating the MSW.However, the WPR may also contain uncertainties,and it may not have been correctly interpreted and documented during the early decades of the CMA best track data(Ying et al., 2014).Accordingly, the primary goal of this study is to evaluate the quality of the aircraft reconnaissance intensity data and its influences on the degree of homogeneity of intensity in the CMA best track dataset.The remainder of this paper is organized as follows.Section 2 describes the datasets and methodology used for evaluation, and section 3 presents our results regarding the evaluation of the MCP.Section 4 presents our results for the evaluation of both the WPR and MSW.Finally, further discussion and conclusions are given in section 5.

2.Data and methodology

2.1.Data

The CMA TC best track dataset includes TC position and intensity as represented by the MCP (hereafter best MCP) and 2-min MSW (hereafter best MSW) values (Ying et al., 2014; Lu et al., 2021).During the aircraft reconnaissance era (1 January 1949 to 15 August 1987), nearly 4% of the best track data were from over land, with support from various meteorological observations across China, while about 12% of the data were from the ocean, with support from the United States aircraft reconnaissance data.The best track data were divided into two groups:reconnaissance-related samples that were defined as the best track data based on aircraft reconnaissance observations(MCP or MSW) within ±3 h and ±1° of longitude and latitude of the data point; and the remaining samples that were unrelated to reconnaissance data (e.g., Fig.1).We use the subscript“B” for the former and “Br” for the latter.It should be noted that the number of samples with a reconnaissance MCP is not equal to the number with a reconnaissance MSW because the reconnaissance MCP and MSW were not always measured at the same time.In fact, 24.9% of the samples with reconnaissance MCP values had no corresponding reconnaissance MSW values.

Fig.1.The distribution of aircraft reconnaissance and best track data for severe tropical storm Sally(1959).The blue solid dots are TC positions from the aircraft reconnaissance data, while the red solid dots and black open dots are the best track data related and unrelated to the aircraft reconnaissance data, respectively.Refer to the text for more details.

The United States aircraft reconnaissance data for TC centers, documented in the CMA Typhoon Yearbook 1949-1987 (Bai et al., 2019), include fix and dropsonde data, which are for TC centers rather than for radial penetration of TCs.The reconnaissance fix data are available from 1949 to 1987 and include the time, TC position, accuracy of position, MCP (denoted as MCPA), MSW (denoted as MSWA), eye shape, diameter, and orientation, as well as corresponding flight-level elements.The flight-level elements,which are available from 1952 to 1987 (e.g., JTWC, 1978;CMA Typhoon Yearbooks 1949-1987), include the height,pressure, temperature, dewpoint, and maximum wind speed and direction.The dropsonde data, corresponded to the fix data, are available in the Yearbooks covering 1956 to 1987.This dataset includes the TC position, geopotential height,pressure, temperature and dewpoint observations.Although the surface pressure as measured by a dropsonde cannot be assumed to equal the MCP (e.g., Hagen et al., 2012), we nevertheless used it as the best estimate of MCP because no better data were available.In contrast, the reconnaissance wind data were not accurate enough and thus were not used as the best estimate of MSW here.The original data of Atkinson and Holliday (1975), including the peak gust observed at stations and estimated storm MCP, were also used to evaluate the WPR.

2.2.Methodology

We used nonparametric statistics in this study because TC intensity, based on either MCP or MSW, has a non-normal distribution.Quantiles were used to describe the basic statistical features of the samples, and nonparametric confidence intervals were used to test whether the intergroup differences of the quantiles were significant (Hutson, 1999).

We used the pruned exact linear time (PELT) algorithm for changepoint detection, which is an exact method and generally produces quick and consistent results (Killick et al.,2012; Haynes et al., 2017a, b).The PELT algorithm works by minimizing a cost function over pruned segments of a time series.According to Killick et al.(2012), for a time seriesYt∈[1,N], assume that the last changepointpdivides the time series into two segmentsYt∈[1,p] andYt∈[(p+1),N],then the corresponding costsCof the two segments will be satisfied by:

for allq＜p＜N, whereKis a constant, andqis assumed to be an optimal last changepoint beforepfor the whole series.According to the inequality, the cost of the time series reduces whenqis an actual optimal value ofp.Therefore, when

there is no optimalqbeforeqfor the series, andpis the optimal last changepoint prior toN.Similarly, we can find the optimal last changepoint forYt∈[1,p].

It is worth noting that changepoints may be associated with either natural or anthropogenic changes.The anthropogenic changes can be further divided into two parts.One is related to the influences of human activities on the natural world and is meaningful for climate change science.The other is the spurious part associated with inhomogeneity,such as changes in instrumentation, development of observational networks, and changes in observation and analysis strategies.Therefore, potential factors causing the changepoints are important for us to examine the homogeneity.

3.Evaluation of the MCP

3.1.Extrapolation relationship of MCP

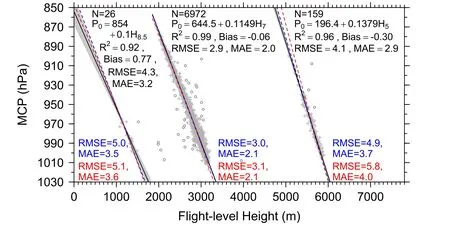
Fig.2.Scatterplot of the minimum central sea level pressure (MCP) and flight-level height.Grey cross symbols denote samples used to fit the linear relationship between MCP and flight-level height, and open circles denote samples excluded from the fitting procedure.N denotes the sample size used for fitting.Black solid lines, with grey shading indicate the 95% confidence intervals, and annotations denote the fittings based on the three groups of samples.The blue dashed lines and annotations are calculated based on Eq.(1)(Jordan, 1958), and the red dashed lines and annotations are based on Eqs.(2)-(4) (Liu and Zhao, 1978).

First, those aircraft reconnaissance fixes with the MCP,flight-level height (FLH), and pressure data available were selected to examine the extrapolation relationship of the MCP.As shown in Fig.2, the selected samples can be roughly divided into four groups: samples with FLH values of ＜ 550 m (＜1500 ft), which were omitted from our analysis; samples with FLH values between 550 and 1800 m,which are associated with flight-level pressures of 850 hPa and cover 9 years (i.e., 1962, 1965, 1967-1972, and 1974);samples with FLH values between 1800 and 3500 m, which are associated with flight-level pressures of 700 hPa and cover the period 1952-1987, and finally, samples with FLH values between 4600 and 6100 m, which are associated with flight-level pressures of 500 hPa and cover the period 1956-1974.The last three groups of samples were preprocessed to exclude outliers and thereby eliminate their unfavorable effects.Accordingly, the relationships were fitted as follows (Fig.2):

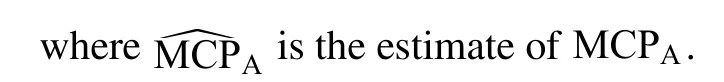
As shown in Fig.2, both the fitting errors and the 95%confidence intervals decrease as the sample size increases.Both the root mean square error (RMSE) and mean absolute error (MAE) show that the errors of Eq.(8) are the smallest among the three fitting relationships.Using Eq.(8) as a reference, Jordan’s (1958) relationship for FLH at 700 hPa is almost the same as Eq.(8), whereas Liu and Zhao’s (1978)relationship overestimates both the low and high tails of the FLHs.Upon extrapolating the FLH at 500 hPa, Jordan’s(1958) relationship more obviously overestimates the high tail of the FLHs compared to that of Liu and Zhao (1978)but underestimates the low part of the FLHs less than that of Liu and Zhao (1978).Upon extrapolating the FLH of 850 hPa, Jordan’s (1958) relationship is more accurate than that of Liu and Zhao (1978) for the high part of the FLHs,whereas the opposite is true for the low part of the FLHs.Although there are slight differences between the extrapolation relationships of the three sources, together they show that the extrapolation from FLH to MCP is relatively reliable.Jordan’s (1958) equation for the FLH at 700 hPa exhibits reactively high accuracy, whereas the equations for the FLHs at both 500 and 850 hPa can be improved by including more samples.

We also evaluated the performance of Eq.(8) when applied to the nonstandard flight-level data, which are mainly around 700 hPa.The data from 600 to 850 hPa were selected and binned using ±5 hPa intervals, and then evaluated by balancing the errors and sample sizes.Our results show that 680-720 hPa may be the optimal level that can be used in Eq.(8) for 700 hPa.When the flight levels are beyond the 680-720 hPa range, both the RMSE and MAE increase with the flight-level biases.

3.2.From the reconnaissance to the best MCP

The reconnaissance MCPs ( M CPA) were compared with the best MCPs that are related ( MCPB) and unrelated to the reconnaissance MCPs ( M CPBr).There are no statistically significant differences (at the 99.9% confidence level)between the reconnaissance MCPs and reconnaissancerelated best MCPs (Fig.3a).Moreover, their annual differences are are not significant (99.9% confidence level)(Fig.3b).This suggests that the reconnaissance MCP data were well incorporated into the CMA best track data.

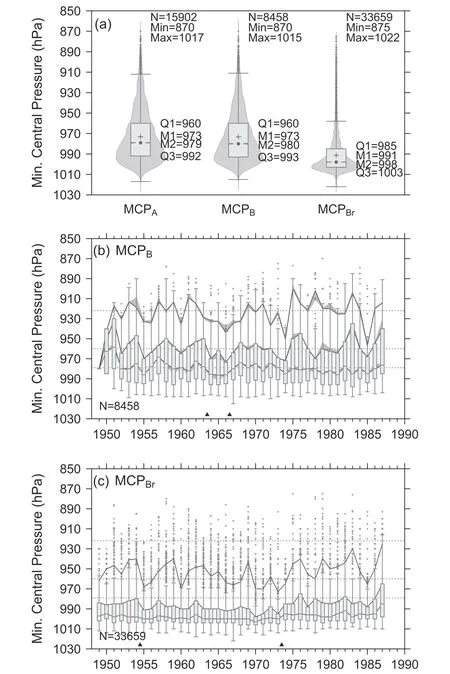
Fig.3.Comparison of MCPs between the aircraft reconnaissance MCPs (MCPA) and the MCPs in the CMA best track data (MCPB and MCPBr), (a) basic statistics and probability distributions; (b) time series of the best MCPs (MCPB ) related to MCPA; and (c) time series of the best MCPs (MCPBr) unrelated to MCPA.N is the sample size, Min the minimum value, Max the maximum value, M1 the mean, M2 the median, and Q1 and Q3 the first and third quartiles, respectively.The solid lines in (b, c) indicate the 5th, 25th, and 50th quantiles and the grey-shaded areas in (b) are the discrepancies relative to the corresponding quantile series of MCPA.The horizontal dotted lines in (b, c) are the 5th, 25th, and 50th quantiles for all samples of MCPA, and the black triangles are the changepoints of the median.

In contrast, the best MCP unrelated to reconnaissance( M CPBr) exhibits a different probability distribution, which is skewed significantly toward high pressures (Fig.3a).For instance, the first quartile of MCPBris higher than the median of MCPB, which indicates that 75% of the samples of M CPBrare located in the higher half of the probability distribution of MCPB.Moreover, according to the WPR used for the CMA best track data (Ying et al., 2014), the difference between the third quartiles of MCPBand MCPBris～10 hPa, which corresponds to a difference in MSW of～9 m s-1.Unlike the best track dataset, which aimed to cover the complete lifespan of all TCs as much as possible,the aircraft reconnaissance was scheduled four times daily for typhoons, but only twice daily for tropical storms,between 1962 and 1965 (JTWC, 1962-1965), and four times daily for all typhoons and tropical storms between 1966 and 1968 (JTWC, 1966-1968), and then four times daily for all TCs since 1969 (JTWC, 1969).This means the sampling strategy of aircraft reconnaissance tends to include more intense samples than weak ones, and so does MCPB.As a result, MCPBrexcludes more intense samples than weak ones, together with all tropical depressions before 1969, the portion of weak samples in MCPBris even larger than that of MCPB.Therefore, the differences between the probability distributions of MCPBand MCPBrmay be attributed partly to the sampling bias associated with the aircraft reconnaissance data.

The potential changepoints of both the annual median series of MCP related and unrelated to aircraft reconnaissance were identified and validated by testing the median differences between every possible pair of segments.Two significant changepoints were identified at the 99.9% confidence level, and are distinct for each series (Fig.3b, c).The two changepoints of the best MCP series related to reconnaissance(Fig.3b) isolated 1964-1966 as a stage with a significantly higher MCP median (986 hPa; 99.9% confidence) than that of the stages pre-1964 and post-1966 (977 and 980 hPa,respectively).The medians of the stages pre-1964 and post-1966 were not significantly different at the 99.9% confidence level.However, the higher median of the MCP for the period 1964-1966 may be attributed to smaller sample sizes of lower pressures than in the other periods (figure not shown), and we found no evidence of non-natural changes associated with the two changepoints.

In contrast, the two changepoints of the best MCP series unrelated to reconnaissance were identified to be 1954-1955 and 1973-1974 (Fig.3c), which found the period with a higher median MCP to be 1955-1973, compared with the lower medians observed in 1949-1954 and 1974-1987.The medians of these three stages are 996,1000, and 995 hPa, respectively.The medians of the MCP for 1949-1954 and 1974-1987 are not significantly different at the 99.9% confidence level, and both are significantly lower than the median for 1955-1973 (99.9% confidence level).Taking the best MCP related to reconnaissance as a reference, we propose that the two changepoints were affected primarily by non-natural factors.Interestingly, both changepoints were associated with special historical stages of the CMA (Hong and Chen, 1983; Wen et al., 2004).

The first changepoint can be related to one of the milestones in observation network development in 1954 when the CMA was transformed from a military organization to a government agency and its organizational structure was reshaped (Hong and Chen, 1983; Wen et al., 2004).According to the instructions of the central government, CMA took action to improve forecasts and warnings for disastrous weather events including TCs in 1954 (Wen et al., 2004).The Temporary Specifications for Surface Meteorological Observations, which set the standards for weather station siting, meteorological instrumentation, and observation practices, has been used nationwide since 1954.Meteorological instruments for routine weather observations have been developed and mass-produced since 1954, despite being underequipped with necessary tools and materials.Marine meteorological observations by fishing vessels began in 1954.Moreover, the number of observatories and weather stations increased from 158 in 1950, to 715 in 1955, and 3240 in 1960 (Hong and Chen, 1983).The number of professional staff in the CMA also greatly increased through continued training, especially with respect to technologies regarding observations, synoptic analysis, and forecasting in the early 1950s (Wen et al., 2004).The quality of observations has gradually improved since 1955.Taken together, these initiatives helped to reform the previously disordered state of the organization and improved the professionalism and accuracy of the meteorological work of the CMA.Although these considerations represent indirect evidence, we believe that such changes in data collection methods over the ocean likely improved TC forecast and warnings beginning in 1954.

The second changepoint occurred during the later period of the Great Cultural Revolution (GCR; 1966-1976).For the CMA, the GCR was a challenging time; however,the early 1970s was a better period compared to the beginning years of the GCR (Wen et al., 2004).China resumed its membership in the World Meteorological Organization (WMO)in 1972, and the CMA then joined the global meteorological telecommunication system (GTS).Following the WMO standards, a type of meteorological facsimile chart receiver,based on low-cost materials, was designed and produced in 1973 and used by the CMA.The radio broadcasting of the facsimile chart began in Beijing in 1974 and was soon extended to the whole country.Some of the challenges facing the CMA, such as data archiving, observation quality, and hiring sufficient numbers of professional staff, were gradually resolved in the early 1970s.New technology related to meteorological satellites attracted much attention, such as the development of a series of satellite image-receiving terminals in 1969 [e.g., Wang, 1974; IAP, 1975; Wen et al., 2004], the use of satellite images (e.g., Wang, 1974; Group of Satellite Imagery Analysis, 1975; Fang et al., 2006), and the expansion of satellite reconnaissance techniques (e.g., Zeng, 1974).In particular, a satellite image-receiving terminal for the National Oceanic and Atmospheric Administration-2(NOAA-2) satellite was developed by IAP/CAS in 1972-1973 and was then gradually used by the CMA.In addition, surface and radiosonde observations were compiled and published during the early 1970s, and some specialized databases, such as those for TCs and cold spells, were also compiled and published as yearbooks and, in turn, added to the regular operational tasks over this period.Furthermore,with the use of the DJS-C8 computer in 1973, global meteorological data were able to be collated more easily.New technology and more observational data may, to some extent, have overcome the problems caused by the GCR, especially after the second changepoint.

4.Evaluation of the MSW

4.1.The WPR

As outlined in section 1, the WPR may be the most accurate approach to estimating the MSW, despite some uncertainties relating to its accuracy.The AH77 WPR, as used operationally by the CMA (Ying et al., 2014), was evaluated in comparison with the relationships fitted to the updated gust factors.That is, the gust factors used in AH77 were the 50th percentiles from table I in LS80, but the updated gust factors were the 90th percentiles from table I in LS80.In addition,we used the recently recommended off-sea gust factor of 1.38 (Harper et al., 2010, hereafter HKG10).As shown in Fig.4a, the AH77 gust factors predict the highest sustained wind speeds, and the other two approaches generate similarly smaller values, although the gust factor in HKG10 predicts an even lower sustained wind speed when the gusts exceed 57 m s-1, and this gap increased with wind speed.The three gust factors were then applied to the raw gust data used in AH77 (listed in Atkinson and Holliday, 1975), and the resultant sustained wind speeds are plotted in Fig.4b.Taking the sustained winds derived in AH77 as the reference, the gust factors of AH77 predict the highest sustained winds, exceeding all of the reference data, whereas the other two gust factors predict sustained winds of less than three-quarters of the reference data.

Using the wind data as reprocessed by applying the gust factors from LS80 and HKG10, the refitted WPRs were compared among the binned and non-binned data.We used the binning method of Landsea et al.(2004).As shown in Fig.4c, the effects of binning are not obvious for the winds reprocessed using the gust factors recommended in LS80, whereas the WPR fitted to the binned data seems to yield a slightly higher MSW than that obtained using nonbinned data for high winds when the winds are reprocessed using the gust factor of 1.38.Referring to the minimum RMSE of the fitted models, the relationship fitted to the reprocessed data using the gust factors recommended in LS80 is as follows (i.e., the blue dashed line in Fig.4c):

This relationship, with an MAE of 4.3 m s-1and bias of 0.5 m s-1, is similar to Eq.(7).The relationship fitted to data reprocessed using the gust factor of 1.38 is as follows (i.e.,the blue solid line in Fig.4c):

The MAE of this relationship is 3.9 m s-1, and the bias is 0.4 m s-1.The difference between the two relationships in Eqs.(9) and (10) may be attributed to the differences between the two kinds of gust factors, which introduce biases of 0%-8%.Relative to the AH77 WPR, the two relationships [i.e., Eqs.(9) and (10)] yield overestimates of 4.4%-7.7% and 0%-14.7%, respectively.

For a particular WPR, its application within the Dvorak technique (Dvorak, 1975, 1984; Velden et al., 2006) is opposite to that used when analyzing aircraft reconnaissance data.The former uses the MSW converted from the current intensity (CI) number to estimate the MCP, whereas the latter uses the MCP to estimate the MSW.Therefore, for the CMA best track dataset, continuous application of the AH77 WPR may not only cause an overestimation of the MSW (i.e., stronger) during the aircraft reconnaissance era,but also induce overestimation of the MCP (i.e., weaker) in the satellite era, and, in turn, may introduce a spurious trend to the long-term variability.

4.2.The reconnaissance MSW

The effects of the three WPRs (i.e., AH77, refitted LS80, and HKG10) on the MSW were further evaluated by comparison of the aircraft reconnaissance MSW with the MSW estimated from the reconnaissance MCP using WPRs.Only reconnaissance data that contained both MCP and MSW values were used in the comparison.Figure 5a shows that the probability distribution of the reconnaissance MSW differs from that of the MSW derived from the MCP,regardless of which WPR is used.In particular, the reconnaissance MSW has a longer tail and more intense extreme winds than either of the derived MSW values.The median of the reconnaissance MSW is statistically different from that of the MSW derived using the refitted LS80 and HKG10 WPRs at a confidence level of 99.9% but is not significantly different from that of the MSW derived from the AH77 WPR at a confidence level of 99.9%.Among the three distributions of derived MSW, the one derived using the AH77 WPR has a longer tail and higher extreme winds than the one derived from the refitted LS80 WPR, and the latter also has a longer tail and higher extreme winds than that derived from HKG10.However, only the difference in the median of the MSW calculated using the AH77 WPR and that derived from the refitted LS80 WPR is statistically significant at the 99.9% confidence level.This may be attributed to the curvilinear characteristics of the gust factors and the associated biases (Fig.4).

Fig.4.Comparison among various wind gust factors and corresponding WPRs.(a) The curves fitted to the gust factors in AH77 and in LS80, and the off-sea gust factor of 1.38 in HKG10; (b) the sustained winds used in AH77,and those converted from raw wind gusts in AH77 using gust factors corresponding to the 50th percentile (open triangles), 90th percentile (blue plus signs), and the off-sea condition (red crosses); (c) the WPRs in AH77 (grey dotted line), refitted in LS80 (grey dashed line), fitted using the wind reprocessed using a gust factor of 1.38 (grey solid line), and that fitted using binned data: “m1” and “m2” denote the mean (blue crosses and plus symbols) and median (red crosses and plus symbols) of the binned data, respectively.The WPRs fitted using the mean are in blue,and those using the median are in red.All RMSEs and MAEs were calculated using the reprocessed non-binned data.

The biases associated with the reconnaissance MSWs from the corresponding estimated MSWs were analyzed at the annual timescale.Taking the biases based on the MSWs estimated using Eq.(9) as an example (Fig.5b), the positive median suggests an overestimation of the reconnaissance MSW, which is significant at the 99.9% confidence level,and the changepoint of the biases, identified and confirmed at 1966-67, indicates the inhomogeneity of the reconnaissance MSWs.The biases before the changepoint have a median of 7.4 m s-1, whereas after the changepoint the median is 1.0 m s-1.Similar results were also found for the biases based on the AH77 and HKG10 WPRs, which confirms the overestimation of the reconnaissance MSWs.In addition, the inhomogeneity of the biases suggests that the reconnaissance data from the early years do not follow any of the three WPRs.Such changes in the WPR were also found in Knapp et al.(2013).

4.3.From the reconnaissance MSW to the best MSW

We next compared the MSW of the CMA best track dataset with the aircraft reconnaissance MSW (Fig.6a, b).There were no statistically significant differences in the three quartiles between M SWAand M SWBover the periods 1949-1966 (Fig.6a), or 1967-1987 (Fig.6b).The difference between the medians of MSWAand MSWBbetween 1949 and 1966 is not significant at the 99.9% confidence level.This indicates that the aircraft reconnaissance MSW data were better incorporated into the CMA best track dataset over the period 1967-1987 compared with 1949-1966.Moreover, the probability distribution of MSWAandMSWBshow longer tails and significantly higher quartiles over the period 1949-1966 than in 1967-1987, which can be attributed to a greater overestimation of MSW during the period 1949-1966 compared with 1967-1987.

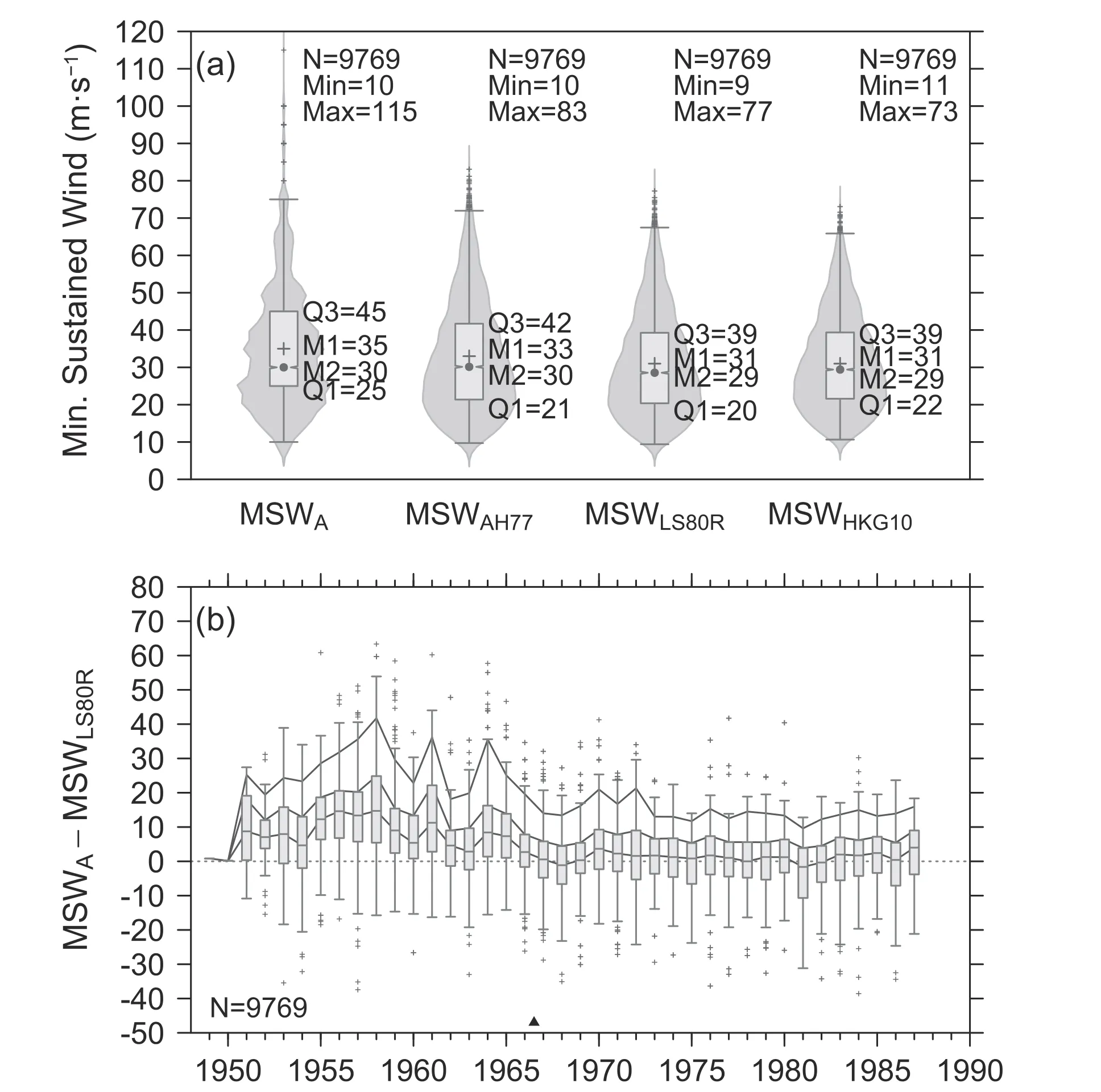
Fig.5.Same asin Fig.3,but for acomparison of the aircraft reconnaissanceMSWs(MSWA) withtheMSWs estimated fromthe reconnaissance MCPs using Eq.(7) (MSWAH77), Eq.(9) ( MSWLS80R),and Eq.(10)(MSWHKG10), (a)Basic statistics and probabilitydistributions and (b) Annual differences between reconnaissanceandestimated MSWs(MSWA-MSWLS80R).In (b), the solid lines are the50th,75th, and95th quantiles, and the black triangle indicates the changepoint.N is the sample size for both MCP and MSW.

When the best MSW unrelated to the reconnaissance( M SWBr) is compared with either the MSWAor MSWB,the probability distributions for both 1949-1966 and 1967-1987 are skewed significantly towards lower wind speeds.The first quartile and median of MSWBrover these two periods are not significantly different at the 99.9% confidence level, although the tail is longer and the third quartile is significantly higher for 1949-1966 compared with 1967-1987.This suggests that the impacts of the reconnaissance MSW on the CMA best MSW may extend, to some extent, to the data unrelated to any reconnaissance, as higher reconnaissance winds may provide more confidence in making higher MSW estimates by analogy and interpolation.

4.4.Overestimation of the best MSW

The overestimation of the best MSW was evaluated by comparison with the MSW estimated from the best MCP,which statistically exhibits the same probability distribution as the reconnaissance MCP (Fig.7).As in section 3b, the best MCP and MSW were divided into two groups of samples;i.e., those related to, and those unrelated to, the reconnaissance MCP.We used Eq.(9) to calculate the estimated MSW based on the results in section 4a.It should be noted that the samples of MSWBand MSWBras shown in Fig.7 are the same as those in Fig.3 rather than those in Fig.6.

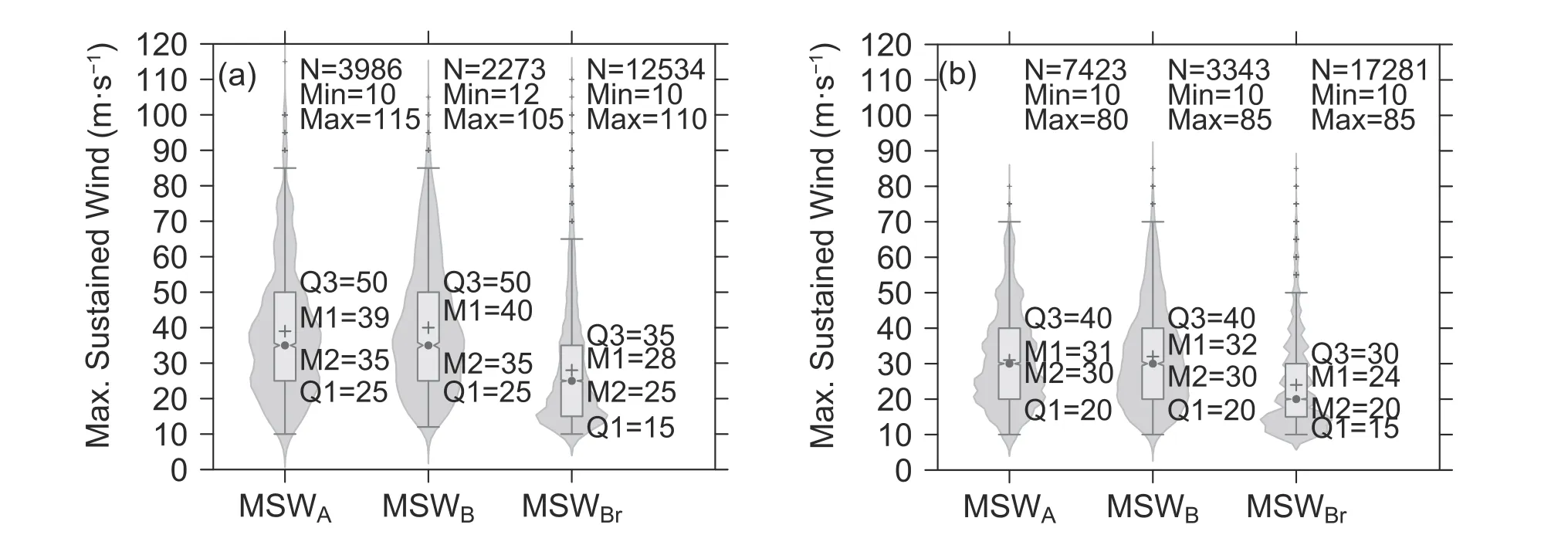
Fig.6.Same as in Fig.3a, but for a comparison of the aircraft reconnaissance MSWs ( MSWA) with the MSWs in the CMA best trackdataset(MSWBand MSWBr) showing the basicstatisticsand probability distributionsfor the samples from the periods(a)1949-1966 and(b) 1967-1987.MSWBdenotes the best MSWs relatedtoreconnaissance MSWs,and MSWBrdenotes thebestMSWs unrelated tothe reconnaissance MSWs.

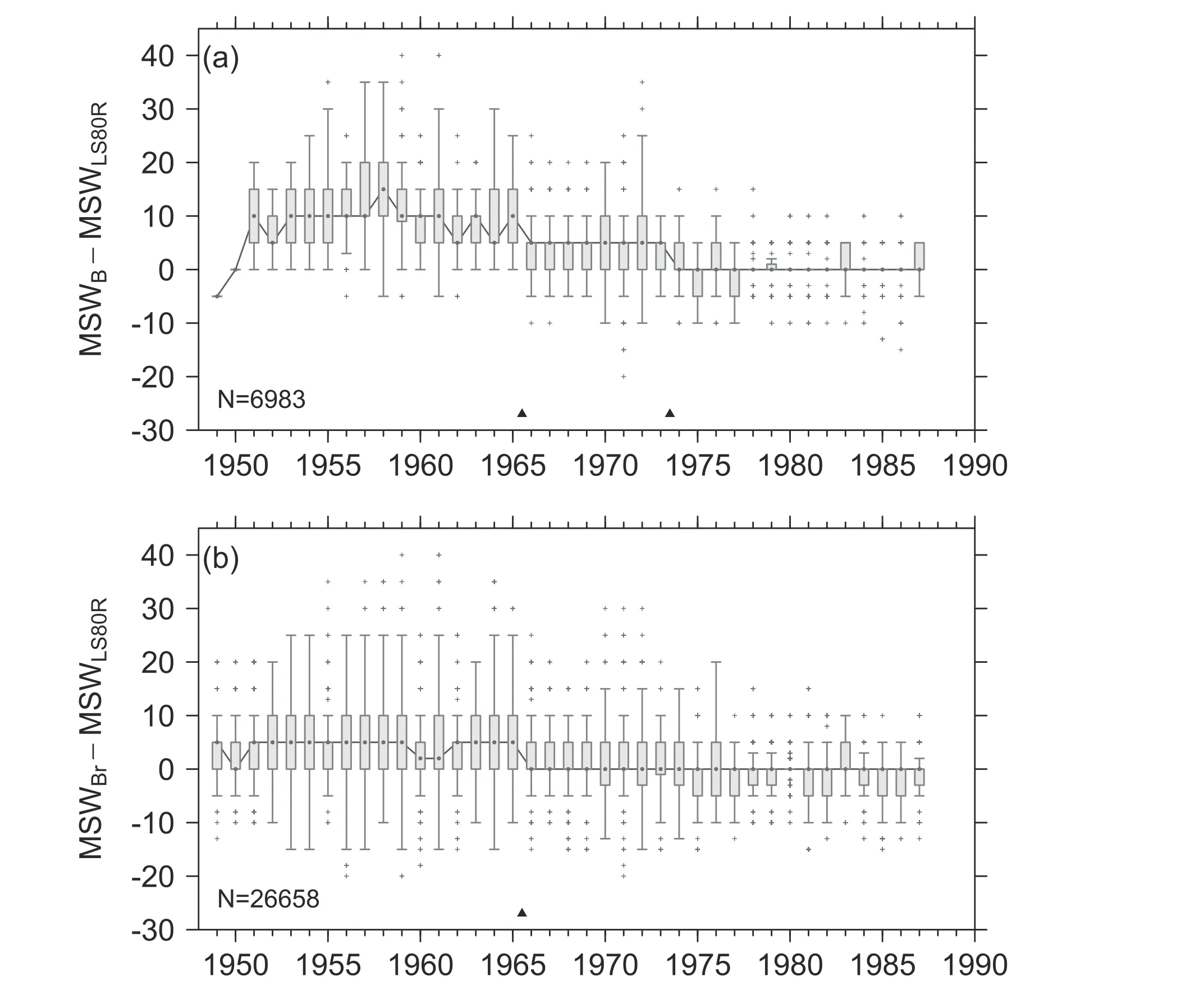
Fig.7.Same as in Fig.5b, but for the annual differences between the best MSWs ( MSWB and MSWBr) and the MSWs estimated from best MCPs ( MSWLS80R ).The MSWB in (a) is related to reconnaissance MCPs rather than reconnaissance MSWs, while the MSWBr in (b) is unrelated to the reconnaissance MCPs.

As shown in Fig.7a, changepoints at 1965-1966 and 1973-1974 were identified and validated in the annual differences series.The changepoints divide the series into three periods with significantly different medians.The median of the first period (1949-1965) is 10 m s-1, of the second period (1966-1973) is 5 m s-1, and of the final period(1974-1987) is 0 m s-1.Therefore, when compared with the best MCP-estimated MSWs ( M SWLS80R), the best MSWs related to the reconnaissance MCPs were found to be overestimated during the first two periods, with the overestimation during the first period being greater.In addition, the two changepoints are markedly different from that of MCPBin Fig.3b, which indicates that the influence of the inhomogeneous best MSWs exceeds the influence of changes in MCPB.This is also confirmed by the annual differences between the best MSWs unrelated to the reconnaissance MCPs and the estimated MSWs (Fig.7b).The only changepoint was detected and validated (at the 99.9% confidence level) at 1965-1966, which is the same as the first changepoint in Fig.7a but noticeably different from that of MCPBrin Fig.3c.Similar results were also obtained when the AH77 and HKG10 WPRs were used to estimate the MSWs, except that a changepoint was detected and validated only at 1967-1968 in the series of annual differences between theMSWBand estimated MSWAH77.As can also be inferred from Fig.5, the inhomogeneous differences indicate that the CMA best track data from the early years do not follow any of the three WPRs.

5.Conclusion and discussion

We assessed the influence of the United States aircraft reconnaissance data on the intensity homogeneity of the CMA best track dataset over the period 1949-1987.We first examined the homogeneity of the reconnaissance data,analyzed how the reconnaissance data were used in the CMA dataset, and then assessed the intensity homogeneity of the CMA dataset by dividing the dataset into reconnaissance-related and reconnaissance-unrelated groups.The WPR, as an important aspect of TC intensity, was also examined, and used to evaluate the MSWs.

Consistent with the results of Knapp et al.(2013), our results suggest that in the period 1949-1987, the MCPs are more reliable and homogeneous than the MSWs, regardless of whether the aircraft reconnaissance data or the CMA best track data are used.These results include the stable fitting of all reconnaissance data using the extrapolation equations for the MCPs developed by Jordan (1958), which confirmed the homogeneity of the reconnaissance MCPs.The better quality and homogeneity of the CMA best MCPs were found to benefit from the incorporation of the reconnaissance MCPs into the dataset, while the remarkable overestimation and inhomogeneity of the CMA best MSWs can be attributed to the incorporation of the reconnaissance MSWs into the dataset.The good agreement between the reconnaissance and best MCPs was reported by Knapp et al.(2013), and they found this phenomenon to be common in the best track datasets issued by various agencies.Our results also show that the overestimation of the reconnaissance and best MSWs was more pronounced prior to the mid-1960s compared with the period after the mid-1960s.The homogeneity of best track data that are not based on reconnaissance data differs from that of best track data based on reconnaissance data.In particular, the best MCP data series unrelated to reconnaissance data appears to include two spurious changepoints in the mid-1950s and mid-1970s, which we propose were generated by changes in the operational practices of the CMA.The best MSWs that are unrelated to reconnaissance data appear to be homogeneous in the lower half of the probability distribution, but inhomogeneous in the upper half, and this may be attributed to having the confidence to make higher estimates when the reconnaissance MSWs provide “observations” with stronger extreme wind.

The AH77 WPR, which is used operationally in CMA,was also examined by using updated gust factors.Our results suggest that the overestimations range from 4.4% to 7.7%, and 0% to 14.7%, for the updated functional and constant gust factors, respectively.Although our evaluation of the WPR was only preliminary and did not consider the influence of all additional factors (e.g., Harper, 2002; Knaff and Zehr, 2007; Holland, 2008; Kossin, 2015) on the WPR, this did not affect our evaluation of data homogeneity.Furthermore, because the WPR was used in reverse ways during the aircraft reconnaissance era and the satellite era, the overestimation caused by the WPR may have been introduced into the MSWs during the aircraft reconnaissance era and into the MCPs during the satellite era.Hence, a spurious trend across the two eras may be hidden in the MCP and MSW data.

Although this study has focused on evaluating the homogeneity of TC data in the period 1949-1987, our ultimate goal is to improve the quality of the CMA TC best track dataset.However, neither reanalysis (e.g., Landsea et al.,2004, 2012, 2014; Hagen et al., 2012; Delgado et al., 2018)nor homogenization (e.g., Kossin et al., 2007) of the TC best track datasets uses the general methods of either numerical model-based reanalysis or statistical homogenization.In terms of the numerical model-based reanalysis, the capability of numerical models to reproduce TCs still seems unable to achieve the goal of improving the quality of the best track data (e.g., Hodges et al., 2017).In addition, some additional issues have been introduced into the procedures; e.g., the TC tracking and detection schemes (Tory et al., 2013a, b;Horn et al., 2014).Regional reanalysis, which shows some advantages over global reanalysis, may introduce other problems (Zhang et al., 2007; Zick and Matyas, 2015).Regarding statistical homogenization (Aguilar et al., 2003; Costa and Soares, 2009; Ribeiro et al., 2016), how to select the reference time series remains a problem because the individual differences among TCs may be large and the identification of matching cases between the reference time series and the target data is thus necessary.In practice, much work remains,including the analysis of as many of the various relevant observations as possible, if we are to achieve the goal of improving the quality of the best track dataset.

Acknowledgements.This work was supported by the Shanghai Natural Science Foundation (Grant No.21ZR1477300).We thank the two anonymous reviewers for their constructive comments, which helped improve the scientific details and writing of the initial manuscript.