计及低电压穿越及故障全过程动态的双馈风电场等值方法
周海强,崔晓丹,许剑冰,曹博源,高 超,陈志昊
(1.河海大学电气与动力工程学院,江苏省南京市 210098;2.南瑞集团有限公司(国网电力科学研究院有限公司),江苏省南京市 211106;3.国网上海市电力公司,上海市 200437)
0 引言
近年来,随着新型电力系统的建设,以风电、光伏为代表的新能源渗透率不断提高,截至2023 年4 月,中国风电、光伏发电总装机容量已达到820 GW,占总发电装机容量的30.9%[1]。新能源机组通过电力电子设备接入电网,与传统同步发电机相比,其控制更为灵活,但惯量较低,且对电压及频率偏差的耐受能力较弱。为满足《风电场接入电力系统技术规定》[2]对故障期间不脱网运行的要求,新能源机组设计了高/低电压穿越、撬棒(Crowbar)等控制策略,并根据运行状态进行切换。同时,为了防止变流器过载,新能源机组还设置了限幅、饱和等环节。因此,新能源机组具有强非线性和离散性,其动态特性复杂,建立准确的风电场模型对于新型电力系统分析至关重要。
由于风电机组动力学模型复杂,而大型风电场机组数量庞大,对每台机组详细建模并进行仿真将面临“维数灾”问题,有必要对风电场进行简化等值。国内外学者对风电场等值建模问题进行了大量研究,其关键在于如何提取各类特征,将具有相似动态特性的风电机组分为一群,进行等值。现有分群方法常依据风电机组的风速、转速、桨距角、Crowbar、电压、短路电流或有功响应等特征量来进行 分 群[3-14]。文 献[3]在 计 及 低 电 压 穿 越(low voltage ride-through,LVRT)控制的条件下,对在不同风速下双馈感应发电机(doubly-fed induction generator,DFIG)的有功响应特性进行比较,提出了基于风速的实用化分群等值方法。文献[4]提出以短路故障前的风电机组转速作为DFIG 风机分群的指标。文献[5]将风速、有功功率和机端电压作为输入变量,应用支持向量机对桨距角控制器动作情况进行辨识,并据此进行分群等值。文献[6]提出根据风电机组运行状态及Crowbar 动作区域判断Crowbar 是否动作。文献[7]应用支持向量机识别Crowbar 状态,并以识别结果和输入风速为分群指标对风电机组进行分群。文献[8]以故障前风电机组的稳态电压为分群指标,应用改进K均值方法对直驱永磁风电机组进行分群聚合。文献[9]提出基于短路电流包络线的结构相似度对风机进行分群。文献[10-11]对DFIG 的LVRT 特性进行了分析,指出单机等值法的误差来源于不同功率水平的风电机组功率恢复时间的差异,提出了通过功率校准提高等值精度的方法。文献[12]针对实际风电场运行信息缺失的问题,提出采用神经网络算法匹配机组信息并进行等值计算。文献[13]提出按照故障稳态有功功率能否恢复至故障前的值对双馈风电机组进行分群等值。文献[14]以根据容量加权法求得的等值参数为初始值,应用粒子群方法对模型参数进行辨识,提高了等值精度。
已有研究取得了大量成果,但总的来说仍存在以下局限:
1)对风电机组的故障全过程动态考虑不足。故障后DFIG 动态过程包括Crowbar 动作、LVRT 控制以及恢复阶段功率爬坡等,已有研究往往只考虑其中某个因素对故障动态的影响,限制了等值模型的适用范围。
2)较少考虑风电场内部电压差异及故障电压的暂态过程。DFIG 机端电压的动态对短路电流、Crowbar 动作以及功率响应特性等有着重要影响[7,13,15],而现有文献常假设DFIG 机端电压与公共连接点(point of common coupling,PCC)电压相等,并认为电压在故障瞬间达到稳态,在考虑风电场内部联接阻抗以及故障点与DFIG 的电气距离时,上述假设将导致较大偏差,从而影响分析结果的准确性。
为此,本文提出了一种计及LVRT 控制及故障全过程动态的双馈风电场等值方法。首先,对计及LVRT 控制的DFIG 故障动态过程进行了分析,计算了故障稳态电压;其次,分析了计及电压暂态条件下DFIG 转子电流的变化机理,提出了基于动作分界线的Crowbar 状态判别方法;然后,根据初始风速及Crowbar 状态对双馈风电场进行分群等值,为提高功率恢复曲线拟合精度,对等值风电场中DFIG的恢复速率进行了分段修正;最后,通过仿真验证了所提方法的有效性。
1 计及LVRT 控制的DFIG 故障动态过程
在短路故障瞬间,为保持磁链不变,DFIG 将感应出较大的定子和转子电流。由于转子侧变流器(rotor-side converter,RSC)容量有限,为避免损坏RSC,常加装Crowbar 电路并采用LVRT 控制,以使故障期间DFIG 可保持一段时间的不脱网运行,并输出一定的无功功率。
1.1 DFIG 的LVRT 控制策略
假设RSC 采用定子电压定向矢量控制,电流正向采用电动机惯例[16-17]。在不计损耗的条件下,DFIG 注入电网的有功及无功功率为:
式中:Pw、Qw分别为风电机组发出的有功和无功功率;Us为定子电压;ird、irq分别为转子电流d、q轴分量;s为 转 差 率;ωs为 同 步 角 速 度;Ls、Lm分 别 为DFIG 定子电感及励磁电感。下文分别以上标pr、fa及po 来标识故障前、故障中及故障后各阶段的变量,如及分别表示故障前、故障中及故障后的定子电压;变量Pw、Qw、ird、irq等以此类推。
故障前稳态时,P及s可由风速根据最大功率点跟踪(maximum power point tracking,MPPT)曲线求得,Q为0。此时,转子电流为:
LVRT 控制通过调节DFIG 转子电流d、q轴分量,向系统提供一定的无功支撑,其在故障不同阶段采取了不同的控制策略。在故障期间,按照风电场并网技术规定要求,当0.2 ≤≤0.9 时,风电机组无功电流增量ΔIQ需满足:
式中:kQ为动态无功电流比例系数,kQ∈[1.5,3.0],本文取1.5;IN为额定电流。由式(3)可知,当=0.2 时,ΔIQ≈IN;当<0.2 时,无功电流已无法继续增大,故取ΔIQ=IN。
故障期间的有功控制有多种方案,如保持有功电流不变或根据机端电压削减有功电流等,本文选择了后者,即
式 中:i为i的 参 考 值;UN为 额 定 电 压。故 障 期间,DFIG 一般采用无功优先控制策略,考虑到转子最大电流的限制,转子电流实际值为:

故障消除后,DFIG 机端电压迅速恢复,风电机组进入恢复阶段。此时的转子电流为:
式中:kr为有功功率恢复速率,一般可取0.2 p.u./s;t2为故障清除时刻。
1.2 DFIG 故障动态过程
计及LVRT 控制的DFIG 机组功率响应曲线如图1 所 示。图 中:t0、t1、t3分 别 为 故 障 发 生 时 刻、Crowbar 退出时刻、恢复完成时刻。
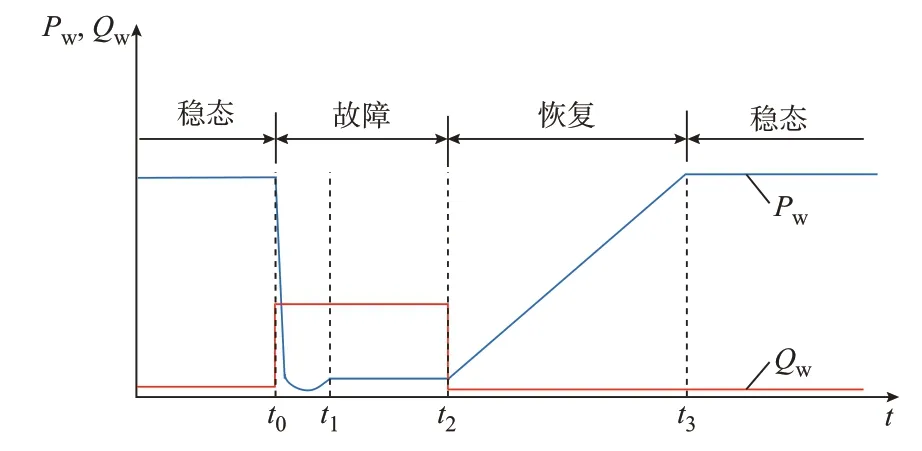
图1 LVRT 控制下DFIG 功率响应曲线示意图Fig.1 Schematic diagram of power response curves of DFIG under LVRT control
故障动态过程一般可分为以下3 个阶段:
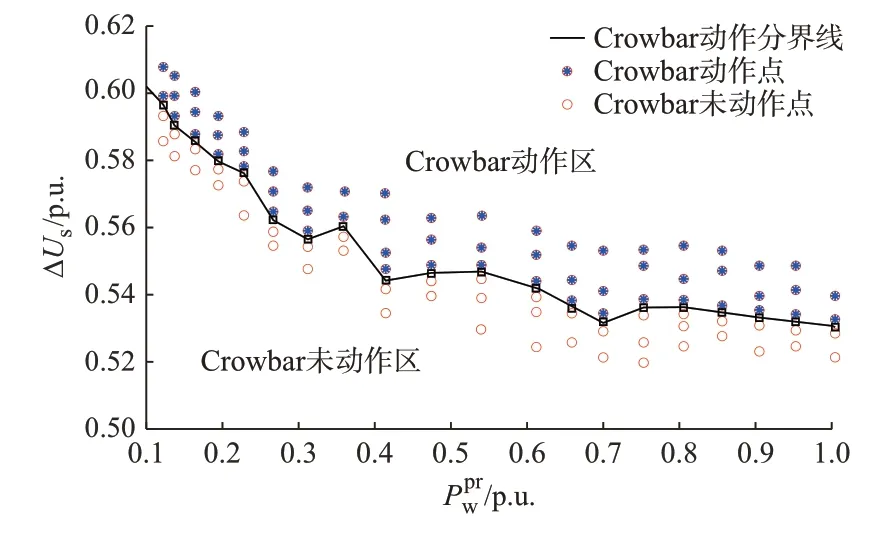
1)t 2)t0≤t 3)t2≤t Crowbar 从导通到退出的时间很短,约为60 ms。在时刻,DFIG 趋于稳态或准稳态,由于此时故障依然存续,将其称为故障稳态。故障稳态既是故障持续期间的终点,又是恢复阶段的起点。设故障稳态时,DFIG 所在节点电压为U,则根据LVRT 控制策略,由式(3)—式(5)可推得DFIG 机组输出有功功率P及无功功率Q分别为: 由此可见,无论Crowbar 是否动作,故障稳态时DFIG 的功率-电压特性不变。因此,Crowbar 是否动作并不改变故障稳态点。 故障稳态电压对于评估电压跌落深度、判断Crowbar 状态具有重要价值。另外,若已知故障稳态电压,则可以确定DFIG 在恢复阶段的初始有功电流,从而计算出功率恢复时间及功率恢复曲线,为等值风电机组恢复速率的设置提供参考。 DFIG 初始稳态是等值计算的基准点,而故障稳态对于分析DFIG 故障过程具有重要意义。因此,有必要对两种状态下的潮流进行计算。 对于含双馈风电场的电力系统,初始稳态时,设第j台DFIG 输出有功功率为P、无功功率为0,j=1,2,…,nw,nw为风电场内DFIG 数量,可将DFIG视为-P的负荷。设U、θ分别为系统各节点的电压及相角向量,ΔU、Δθ分别为电压及相角修正量,ΔP、ΔQ分别为节点有功及无功不平衡量,则系统功率修正方程为: 式中:mj为潮流计算时第j台DFIG 所在节点的编号;U为 第j台DFIG 的 故 障 稳 态 电 压。将 式(10)、式(11)代入故障稳态时的功率修正方程,经过迭代求解,即可得出故障稳态时DFIG 的U及θ。 尽管Crowbar 是否动作不改变故障稳态点,但其将影响系统到达故障稳态的暂态过程。若Crowbar 动作,则DFIG 在短时间内将作为异步电动机运行;若Crowbar 未动作,则DFIG 将一直由RSC按照LVRT 控制策略进行控制。因此,Crowbar 是否动作将导致DFIG 在[t0,t1]时段内表现出不同的暂态特性。在双馈风电场等值时,为了将具有相似暂态特性的DFIG 划为一群,需要判断故障过程中Crowbar 是否动作。 Crowbar 是否动作取决于短路故障发生时DFIG 转子电流的大小。国内外不少学者对DFIG短路电流计算开展了研究,并取得了有益的成果[15-16,18]。假设电流内环控制回路闭环带宽足够大,RSC 交流侧输出电压能够无差地跟踪参考值,则转子电流动态方程为: 对于单台DFIG 与无穷大电网相连的情况,若故障点位于DFIG 机端,则可忽略定子电压暂态,即认为电压瞬间跌落至稳态值。设定子电压跌落幅值为,定义电压跌落系数ku为: 则故障后定子磁链为: 式 中:τ=jωs+Rs/(σLs)。 将 式(14)代 入 式(12)得: 式 中:a1=(Rr+kp)/(σLr);b1=ki/(σLr);c1=b1;d1=Lmτ2/(jωsσLrLs)。根据式(15)可求出转子电流的解析解,其公式详见文献[7],限于篇幅,本文不再赘述。由式(15)可知,对于单机系统,短路电流与DFIG 参数、电流内环控制器参数、电压跌落深度及故障前转子电流参考值等相关。此时,可以直接根据解析公式计算转子电流,并据此判断Crowbar 是否动作。 在实际工程中,双馈风电场内DFIG 通过升压变压器、集电网络以及输电线路联接到外部系统的故障点,其联接阻抗不可忽视。故障时,DFIG 定子电压Usf(t)将经历如附录A 图A1 所示的过渡过程[19]。此时,若忽略电压暂态,直接按照式(15)计算转子电流将导致较大偏差,从而误判Crowbar 状态。为此,本文提出了一种基于动作分界线的Crowbar 状态判别方法。 计及电压暂态时,Usf(t)是一个振荡衰减过程。设故障后Crowbar 在tc时刻动作(tc约为故障后10 ms),则[t0,tc]时段内Usf(t)波形将对Crowbar 是否动作有着重要影响。 尽管难以写出Usf(t)的解析表达式,但在故障后极短时间内,可近似认为Usf(t)按指数规律衰减。1.2 节中已经证明,Crowbar 是否动作不会影响U。因此,如果Usf(t)按照[t0,tc]时段内的规律继续演变,其终态将趋于U。[t0,tc]时 段 内Usf(t)可 近似为: 式中:Tu为故障电压衰减时间常数,其取决于DFIG与故障点之间的阻抗。一般情况下,外部系统故障点与PCC 之间的联接阻抗远大于风电场内部的联接阻抗,故可认为风电场内各DFIG 的Tu近似相等。由式(16)可见,在计及电压暂态的条件下,尽管无法直接根据式(15)计算转子电流,但U及U仍然对[t0,tc]时段内Usf(t)的动态及转子电流有着关键性作用。 离线仿真时,应保持外部系统结构和参数不变,为加速计算,可将双馈风电场替换为1 台等值机。首先,在给定Pprw(或风速)下,通过改变DFIG 与PCC 的 电 气 距 离 来 调 节ΔUs,找 出 给 定Pprw下Crowbar 动作所对应的最小ΔUs;然后,改变风速,在不同Pprw下重复同样操作;最终,通过对一定数量样本的仿真计算,可得出Crowbar 动作分界线。 以本文算例系统为例,图2 给出了基于100 个样本场景求得的Crowbar 动作分界线。在某个场景下,若DFIG 的(Pprw,ΔUs)位于动作分界线上方,则故障后Crowbar 将动作,否则Crowbar 将不动作。对多个不同电压跌落深度及不同时长故障的测试结果表明,基于动作分界线的判断结果与实际仿真完全吻合。 图2 Crowbar 动作分界线Fig.2 Division line of Crowbar operation 双馈风电场分群需要考虑DFIG 在故障持续阶段及故障恢复阶段的动态相似性,但由于分群数量受到限制,实际分群时很难兼顾2 个阶段的动态特性。考虑到恢复阶段控制及功率特性相对简单,本文采取了根据故障持续期间动态特性进行分群等值,再对等值模型的恢复特性进行修正的方法。 根据Crowbar 是否动作,可将双馈风电场内的DFIG 分 为 两 大 类。Crowbar 动 作 时,DFIG 可 视 为感应电机,其动态特性主要取决于初始转差率s0,而根据MPPT 曲线可求出不同风速下DFIG 的P和s0。 附录A 图A2 给出了Crowbar 动作时,不同风速下DFIG 在故障持续期间的功率响应特性。由图A2 可见,当风速v位于9 m/s 两侧时,其动态特性有较大差异。风速较小时,短路故障后有功功率下降过程中振荡较为明显;风速较大时,有功功率的下降过程将不存在振荡。因此,根据初始风速可将Crowbar 动作的DFIG 分为2 群。对于Crowbar 未动作的机组,由于不同风速下其在故障期间的动态特性相差不大,可将其等值为1 群。 由此,双馈风电场分群准则为:1)故障期间Crowbar 动作,且风速v≤9 m/s 的DFIG 划分为C1群;2)故障期间Crowbar 动作,且风速v>9 m/s 的DFIG 划 分 为C2群;3)故 障 期 间Crowbar 未 动 作 的DFIG 划分为C3群。 为了提高等值精度,可进一步按照高、中、低风速将Crowbar 动作的DFIG 机群进行细分,但分群数量越多,计算量越大,实践中需要平衡对等值精度和简化程度的要求,合理设定分群数。 集电网络参数可改变风电场内潮流分布、功率损耗以及机端电压分布等,对系统动态特性有着重要影响。目前,常基于网络损耗不变、加权电压差不变等原则[7]来进行集电网络等值,求取聚合参数,但其精度仍有待进一步提高。为此,本文基于注入电流不变原则对集电网络等值参数进行了计算。 设某群内有nC台DFIG,该群被等值为1 台等值机Weq,Weq与PCC 的联接阻抗为Zeq。根据注入电流不变的原则,等值机Weq注入并网点的电流İeq为: 式 中:Qw,i、U̇w,i分 别 为 第i台DFIG 的 无 功 功 率、电压;conj(⋅)为 共 轭 算 子。因 此,Weq所 在 节 点 电 压 为 由此可得: 式中:U̇pcc为风电场并网点电压。上述方法具有严格的物理意义,且计算简便,可根据故障前稳态潮流方便地求出Zeq。 为了保持风电场PCC 无功功率不变,可在PCC处并联一补偿电容Ccomp,以提高等值模型无功精度。Ccomp计算公式为: 式中:Qpcc、Qpcc,eq分别为等值前、后风电场注入PCC的无功功率。 故障清除后,DFIG 进入功率恢复阶段,其有功功率以速率kr上升,直至故障前稳态功率,但由于DFIG 的恢复时间各不相同,等值模型的功率恢复特性往往存在一定偏差。为此,本文提出了一种等值风电场功率恢复特性修正方法。 若忽略t2时刻风电功率的暂态过程,则根据式(1)和式(6)可推出,在功率恢复阶段: 式 中:tre,j为 第j台DFIG 的 功 率 恢 复 时 间。 由式(20)可推出: 由于场内DFIG 具有不同的U及P,其恢复时间也各不相同。 将风电场内nw台DFIG 的功率恢复时间从小到大排序,设所得数组为Tre,则恢复阶段PCC 输出风电功率P(t)为: 式中:k=2,3,…,nw;Sw为单台DFIG 额定容量。 由此可见,风电场输出功率曲线Ppopcc(t)为一条nw段的折线,其斜率逐渐减小,直至故障后稳态时斜率为零。 附录A 图A3 以本文算例系统为例,给出计算得到的功率恢复曲线与实际曲线对比图。由图A3可见,计算曲线可较好地拟合实际风电场的功率恢复过程。因此,可根据该曲线对等值模型的恢复特性进行修正,以提高等值模型的精度。 等值DFIG 恢复速率分段修正原理如图3 所示。图中:等值风电场功率恢复曲线P(t)为neq段折线,neq为等值机数量;P(t)为根据式(22)计算出的功率恢复曲线。 图3 等值DFIG 恢复速率分段修正原理图Fig.3 Principle diagram of segmented modification ofpower recovery rate of equivalent DFIG 综合考虑故障持续阶段及恢复阶段动态的等值方法如图4 所示。首先,计算初始稳态及故障稳态潮流,对电压跌落深度进行评估,并对功率恢复曲线进行预测;然后,根据Crowbar 动作分界线,判断DFIG 在故障期间是否动作,再根据分群准则将DFIG 分为3 群,初步计算风电场等值模型;最后,根据功率恢复曲线对等值机的恢复速率进行分段修正。该方法将分群等值与参数修正相结合,使得等值模型在故障各阶段均具有较好的精度。 图4 考虑故障全过程动态的等值方法流程图Fig.4 Flow chart of equivalent method considering dynamics of entire fault process 为了验证所提双馈风电场等值方法的有效性,基于MATLAB 2019/Simulink 仿真平台,构建了如附录A 图A4 所示的含双馈风电场算例系统,并对其进行了等值运算。 算例中双馈风电场共含18 台DFIG,其中,DFIG 采用Simulink 提供的详细模型,并在此基础上增设了Crowbar 电路模块及LVRT 控制模块。DFIG 经575 V/25 kV、25 kV/220 kV 两次升压后,在节点3 接入外部电网,外部电网由电源及阻抗Zs1、Zs2构成,节点2 为故障点。系统基准容量为100 MV∙A,额定频率为60 Hz,各线路参数如附录B表B1 所示。 风电场内各DFIG 风速及稳态功率如附录B表B2 所示。单台DFIG 额定功率为4.5 MW,容量为5 MV∙A,Lm、Ls、Lr分别为2.90、3.08、3.06 p.u.,Rs、Rr分 别 为0.023 p.u.和0.016 p.u.,惯 性 时 间常数H为5.005 s。变压器T1至T18额定容量为5.25 MV∙A,短路阻抗为(0.002+j0.05)p.u.;变压器Tpcc额定容量为100 MV ∙A,短路阻抗为(0.004+j0.06)p.u.。 设0.5 s 时节点2 发生三相对地短路故障,接地阻抗Zf为0.21 Ω,20 个周期(约0.333 3 s)后故障清除,取步长为5 μs,对系统进行仿真计算。仿真使用Intel Core i7/4.7 GHz 电脑及MATLAB R2019b/Simulink 软件。 首先,对计及LVRT 控制的故障稳态潮流进行了计算,DFIG 机端电压如附录B 表B3 所示,其结果与Simulink 仿真结果基本吻合。由表B3 可以看出,W1、W18的 故 障 稳 态 电 压 分 别 为0.349 3 p.u.和0.527 5 p.u.,不同的DFIG 电压跌落相差很大,这也验证了等值过程中考虑风电场内电压差异的必要性。接着,根据DFIG 风电功率P及电压跌落ΔUs,并结合离线计算得到的动作分界线,判断Crowbar 是 否 动 作。在 本 算 例 中,W15、W16、W17及W18对应的点(P,ΔUs)位于分界线下方,故可判断故障后其Crowbar 电路将不会动作。 根据DFIG 分群准则,双馈风电场被划分为C1、C2、C3共3 群。其 中,{W3,W5,W9,W10}为C1群;{W1,W2,W4,W6,W7,W8,W11,W12,W13,W14}为C2群;{W15,W16,W17,W18}为C3群。由此可构建如图5 所示的等值系统,各等值机及联接线路参数如附录B 表B4 所 示。 图5 等值系统原理图Fig.5 Principle diagram of equivalent system 分别应用详细模型及等值模型对故障后5 s 的系统动态响应进行了仿真,图6 给出了并网点有功功率、无功功率及电压响应曲线对比图。由图6 可见,在故障持续期间(0.500~0.833 s),各曲线均具有较高精度。在恢复阶段,无功及电压曲线仍具有较高精度,但有功曲线的误差稍大。这是因为实际系统中18 台DFIG 依次完成恢复,其功率恢复时间各不相同,有功恢复曲线基本为一条平滑曲线,而等值系统用3 台等值DFIG 替代原有风电场,故有功恢复曲线存在一定偏差。为了提高恢复阶段等值模型的精度,应用4.2 节所述方法对等值DFIG 恢复速率进行分段修正,其结果如表1 所示。修正后等值模型有功恢复曲线如图6(a)所示。 表1 等值DFIG 分段恢复速率Table 1 Segmented power recovery rate of equivalent DFIG 图6 等值模型及详细模型故障响应曲线对比Fig.6 Comparison of fault response curves between equivalent model and detailed model 为了比较等值模型精度,定义等值误差ey为: 式中:y表示有功或无功功率;ypcc,h、yˉpcc,h分别为详细模型及等值模型在PCC 输出变量y在采样时刻h的取值;Ns为样本总数,本算例中取样间隔为0.000 1 s。对恢复阶段(0.833~3.500 s)的有功响应曲线进行分析,计算表明,修正前后等值模型的有功误差分别为3.29%及2.05%。由此可见,对恢复速率分段修正提高了恢复阶段的等值精度。 对风电场而言,准确计算并网点短路电流及短路电压的瞬时值波形对于保护参数整定、暂态电压稳定分析等具有重要作用。为此,对等值前后并网点的短路电流及短路电压的瞬时值波形进行了对比。以A 相为例,对比结果如附录A 图A5 所示。由图A5 可见,等值模型与详细模型求得短路电流最大值及波形基本一致,而等值后电压波形基本不变。 另外,仿真还表明,若使用详细模型,则仿真5 s动态过程需用时5 951 s,而使用等值模型进行仿真仅需要用时110 s。由此可见,等值模型可有效地简化系统,使计算速度大为提高。 为了考核所提方法的性能,将其与2 种常用的等值方法进行了比较: 1)方法A:不考虑Crowbar 状态,根据风速分群,参考文献[3],以7 m/s、12 m/s 为分界点,将风电场内DFIG 划分为3 群进行等值。 2)方 法B:根 据Crowbar 是 否 动 作 将DFIG 分为2 群。 2 种方法所得的等值模型参数分别如附录B 表B5 和表B6 所示,不同等值模型的功率响应特性对比如附录A 图A6 所示。 表2 对不同等值方法的精度进行了比较。为更好地反映等值模型在故障各阶段的精度,分别用eP1、eQ1表示故障持续阶段的有功及无功误差,而eP2、eQ2则表示恢复阶段的有功及无功响应误差。需要说明的是,由于本文研究的故障较为严重,故障持续阶段输出有功较小,故计算得到的相对误差eP1偏大,如本文所提方法的eP1为8.24%。但是,从附录A 图A6(a)可以看到,在0.500~0.833 s 时段内,等值前后有功响应曲线几乎完全吻合,其绝对偏差很小。同样,恢复阶段的无功相对误差eQ2数值也偏大。 表2 不同等值方法的等值精度对比Table 2 Comparison of equivalency accuracy of different equivalent methods 由表2 可见,尽管方法A 将双馈风电场等值为3 群,但由于分群时未考虑Crowbar 动态,其在故障持续阶段的有功误差eP1及无功误差eQ1很大。方法B 将双馈风电场等值为2 群,其中,所有Crowbar 动作的DFIG 等值为1 群。与方法A 相比,方法B 在故障持续阶段的精度有所提高,但由于模型过于简单,其在故障恢复阶段的精度较低。 总体来看,本文所提方法综合考虑了故障持续阶段及恢复阶段的动态,具有较好的等值精度,这也验证了等值过程中考虑故障全过程动态的必要性。 本文提出了一种考虑故障全过程动态的双馈风电场等值方法,主要成果包括:1)对LVRT 控制下故障各阶段动态进行了分析,提出了基于故障潮流的DFIG 电压跌落计算方法;2)在考虑电压暂态的条件下分析了短路电流变化的机理,提出了基于Pprw-ΔUs平面上的动作分界线判断Crowbar 状态的方法;3)提出了基于初始风速和Crowbar 的双馈风电场分群准则,以及等值DFIG 恢复速率分段修正方法。 本文方法在故障各阶段均具有较好精度,所得模型既可用于故障后几百毫秒的电压、电流计算,也可用于数秒时间内的机电暂态分析,具有较好的适用性。需要说明的是,本文主要针对三相对称故障进行研究,不对称故障下的等值问题将是下一步研究的重点。 附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx),扫英文摘要后二维码可以阅读网络全文。1.3 DFIG 初始稳态与故障稳态的计算
2 故障过程中Crowbar 的状态判断
2.1 忽略电压暂态的DFIG 短路电流计算

2.2 计及电压暂态的Crowbar 状态判别方法

3 双馈风电场分群及聚合等值
3.1 考虑风速及Crowbar 状态的DFIG 动态分群
3.2 DFIG 参数聚合

3.3 风电场集电网络等值
4 等值双馈风电场功率恢复特性修正
4.1 DFIG 及双馈风电场的功率恢复特性
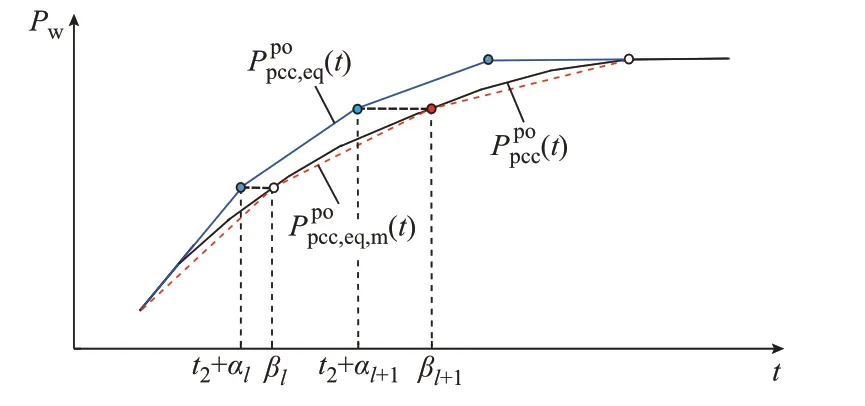
4.2 等值DFIG 恢复速率分段修正

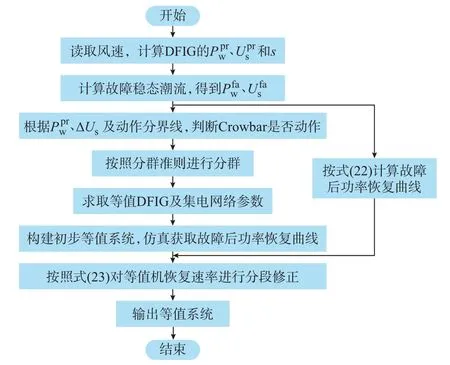
4.3 综合考虑故障全过程动态的等值方法
5 算例分析
5.1 算例系统
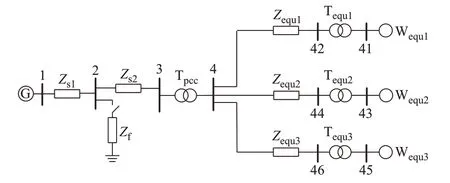
5.2 双馈风电场等值模型
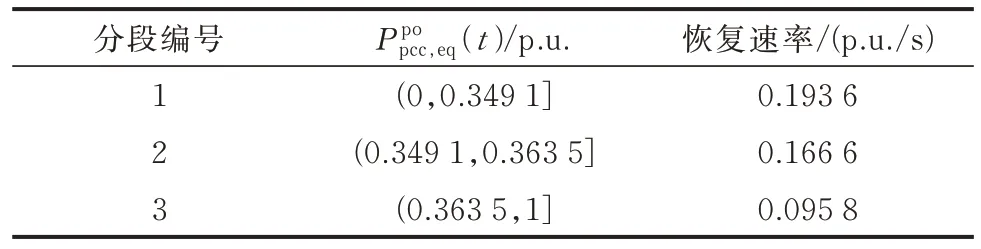
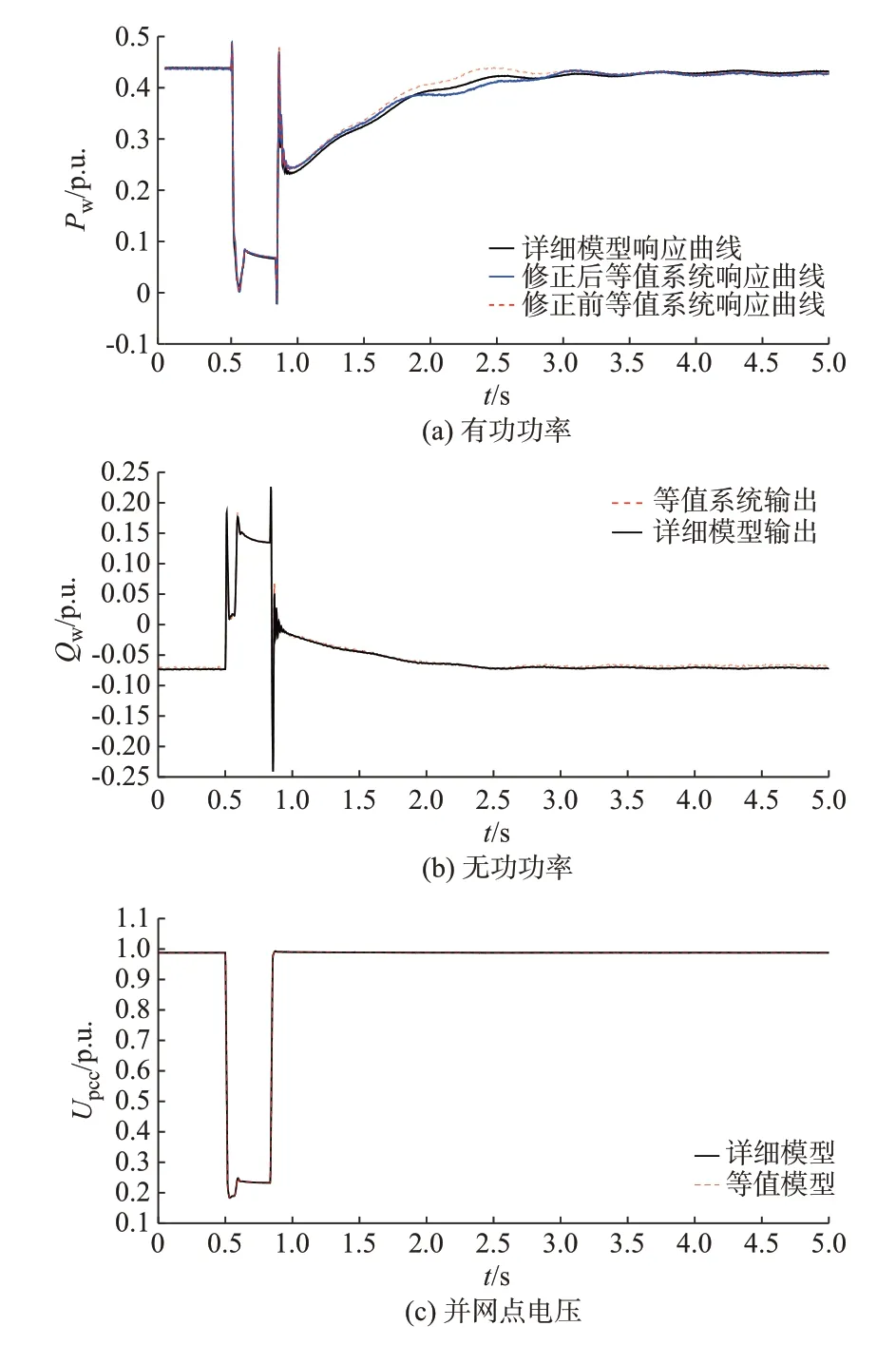
5.3 双馈风电场等值模型响应特性分析
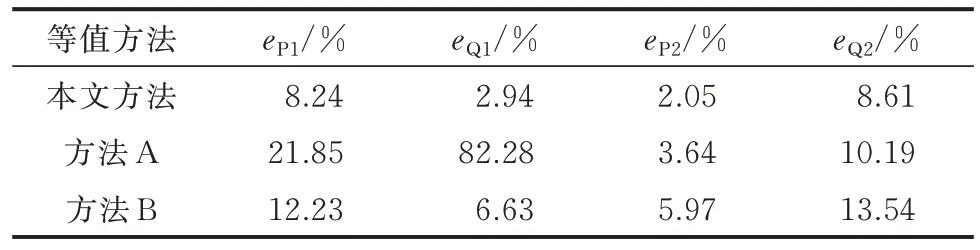
5.4 不同等值方法对比
6 结语

