哈里斯鹰算法在广义非线性马斯京根参数优化中的应用
陈海涛 赵志杰

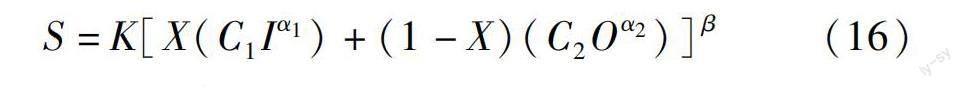
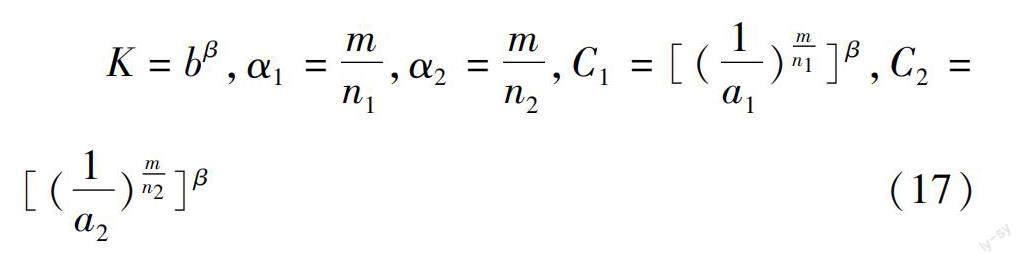
摘要:马斯京根模型在河道洪水演算中发挥着重要作用,其演算精度在于参数的优选。针对目前马斯京根参数率定中存在的求解复杂、精度不高等问题,提出利用哈里斯鹰算法对其参数进行优化,这种方法具有广泛的全局搜索能力,且需要调节的参数较少。以黄河支流洛河为研究对象,利用广义非线性马斯京根模型对宜阳—白马寺段的河道进行洪水演算,且分别用哈里斯鹰算法、粒子群算法和蚁群算法对其参数进行优化。结果表明,基于哈里斯鹰算法的广义非线性马斯京根模型在洛河宜阳—白马寺段的演算精度较高,其Min.SSD为1 237,洪峰误差DPO仅为5,均优于粒子群算法和蚁群算法优化后的结果,其成果适合应用于洛河宜阳—白马寺段的洪水预报工作。
关键词:洪水预报;广义非线性马斯京根模型;哈里斯鹰算法;参数率定
中图分类号:TV21文献标识码:A文章编号:1001-9235(2024)02-0060-09
Application of Harris Hawks Optimization Algorithm in Optimization of Generalized Nonlinear Muskingum Parameters
——A Case Study of the Luohe River
CHEN Haitao,ZHAO Zhijie*
(College of Water Resources,North China University of Water Resources and Electric Power,Zhengzhou 450046,China)
Abstract:The Muskingum model plays an important role in river flood simulation,and its simulation accuracy relies on the optimal selection of parameters.To address the current challenges in parameter calibration for the Muskingum model,such as complex solution processes and low accuracy,the use of the Harris Hawks optimization (HHO) algorithm was proposed to optimize its parameters.HHO algorithm has a wide range of global search capabilities,with fewer parameters to be adjusted.Taking Luohe River,a tributary of the Yellow River,as the research object,the generalized nonlinear Muskingum model was used to simulate the flood in the Yiyang-Baimasi section of the river.The parameters were optimized by employing the HHO algorithm,particle swarm optimization (PSO) algorithm,and ant colony optimization (ACO) algorithm,respectively.The results show that the generalized nonlinear Muskingum model based on the HHO algorithm achieved high simulation accuracy in the Yiyang-Baimasi section of the Luohe River,with a Min.SSD of 1 237 and the flood peak error (DPO) of only 5,outperforming those obtained through optimization using PSO algorithm and ACO algorithm.The results are suitable for application in flood forecasting in the Yiyang-Baimasi section of the Luohe River.
Keywords:flood forecasting;generalized nonlinear Muskingum model;Harris Hawks optimization (HHO) algorithm;parameter calibration
自古以來,洪水灾害一直困扰着人们,导致群众生命财产安全受到严重影响,为应对洪涝灾害带来的不利效应,人们采取了大量的措施进行防治,通常包括工程措施和非工程措施,工程措施主要包括修建堤坝、水库,治理河道等;非工程措施主要有洪水预报、洪水调度、洪水警报等[1]。洪水预报中最重要的工作是河道洪水的演算,其方法主要有:马斯京根法、特征河长法、经验槽蓄曲线法和一、二维水动力模型分析法等[2],其中马斯京根法是最为常用的一种方法。
马斯京根模型由McCarthy在1938年提出,以首次应用于美国的马斯京根河而闻名。马斯京根法是计算河道流量演算最常用的水文学方法,虽然该方法简单,却拥有一定的实用价值,至今都被广泛应用。如Saeed等[3]利用三参数马斯京根模型对Wilson洪水进行了演算;LING等[4]利用马斯京根模型对1982年10月的Wyre River洪水、1960年12月和1969年1月的Wyre River洪水进行了演算;黄兴春等[5]利用马斯京根模型对泸州、赤水和朱沱3站之间的河道进行了流量演算。
用马斯京根模型来进行河道流量演算的精度取决于对其参数的估计,这也是该方法的主要难点[6]。以前常用的方法是试算法、矩法、最小面积法和最小二乘法等[7],但这些方法计算繁琐,精确度不高,因而许多研究者开始采用智能算法[8]对其参数进行优化。如崔东文等[9]利用MFO算法对马斯京根模型参数进行优化,获得比其他文献中相关研究更为精准的洪水拟合过程;张昊等[10]在计算马斯京根模型参数时,对其中的流量比重系数采用SCE-UA算法进行了优化,相较于其他传统的方法,该算法计算出来的参数其结果更优,为精确估算考虑支流汇入的马斯京根模型参数演算提供了一种很有效实用的方法,使得模型求参过程变得更加优越和简单化;欧阳俊等[11]在优化非线性马斯京根模型参数时,采用随机分形搜索算法对其参数进行优化,且用混沌序列来替代随机数,使得非线性马斯京根模型的求参数过程变得更加简便,且参数解算精度更高。
马斯京根模型主要是由水量平衡方程和槽蓄方程联立推导而来,在以往的研究中,大多数研究人员主要关注的是槽蓄方程的计算层面,通过选取不同的计算方法进行参数优选,从而得到理想的结果;而最近,一些研究者开始专注于槽蓄方程的结构层面,通过改造槽蓄方程的结构[12],赋予马斯京根模型更多的参数,使其获得更大的自由度,从而使洪水数据拟合结果更加准确,其适应度更强。
本文利用改造槽蓄方程结构后的广义非线性马斯京根模型对洛河宜阳—白马寺段的河道进行洪水流量演算,且通过哈里斯鹰算法对其参数进行優化,其结果可为洛阳市的洪水预报作业提供参考依据和为其他河道洪水演进研究提供思路。
1 优化模型
1.1 哈里斯鹰算法数学描述
哈里斯鹰算法(Harris Hawks Optimization,HHO)是由Heidari等[13]在2019年提出的,是一种模拟哈里斯鹰捕食行为的智能优化算法,其优点在于能够对全局进行广泛的搜索,具有很快的收敛效应以及调节参数较少等,目前该算法已经被广泛应用于多个领域。哈里斯鹰算法的数学模型如下。
a)参数设置和种群初始化。设置哈里斯鹰种群规模N、所要迭代的最大次数T并进行种群初始化。假设种群规模为N的哈里斯鹰种群有(X1,X2,…,XN)T,其初始位置矩阵为为式(1):
式中 Xi,j——第i只哈里斯鹰在第j个维度相应的值;N——哈里斯鹰种群规模;d——搜索空间维数。
为了计算每只哈里斯鹰的目标适应度函数值,列出相应储存适应度函数值的矩阵,见式(2):
b)调整每只新哈里斯鹰所处位置,同时不断更改新捕食对象的位置与逃逸能量。哈里斯鹰在捕猎过程中,会根据捕食对象自身的逃逸能量E进行不同的捕猎行为,E的计算见式(3):
式中 E0——捕食对象的初始能量,在[-1,1]之间进行随机取数,且该数值每次迭代都将自动更新;t——迭代次数;T——最大迭代次数。
c)搜索阶段。当|E|≥1时,哈里斯鹰广泛分布在不同位置进行搜寻猎物,此时随机生成一个数q,进行如下搜索方式的选择:
式中 X(t)——哈里斯鹰目前所在的位置;X(t+1)——哈里斯鹰下一次迭代时所处的位置;Xrand(t)——哈里斯鹰随机选择的位置;Xrabbit(t)——捕食对象所在位置;ub、lb——维度变量的上下限;r1、r2、r3、r4、q——[0,1]之间随机的数;Xm(t)——哈里斯鹰群体的平均位置,表达式为:
式中 Xk(t)——哈里斯鹰群体中第k个个体的位置;N——种群规模。
d)捕食阶段。当|E|<1时,哈里斯鹰进行捕猎行为,根据|E|和r的随机取值进行不同的捕猎方式,由于在以往的研究中,关于哈里斯鹰算法介绍的文献较多,具体捕猎方式数学公式可参考相关文献。以下仅对捕猎策略的选择进行简单介绍:①当0.5≤|E|<1且r≥0.5时,采用软围攻的方式进行捕猎;②当|E|<0.5且r≥0.5时,采取硬围攻的方式进行捕猎;③当0.5≤|E|<1且r<0.5时,采取渐进式快速俯冲的软包围方式进行捕猎;④当|E|<0.5且r<0.5时,采取渐进式快速俯冲的硬包围方式捕猎。
e)终止条件。若当前迭代次数大于等于最大迭代次数,则输出当前的最优解,否则继续进行搜索。
1.2 广义非线性马斯京根模型
广义非线性马斯京根模型由Omid Bozorg-Haddad等[14]提出,该模型主要针对槽蓄方程的结构进行了改进,由原来的3个待优化参数[15]变为现在的8个待优化参数。广义非线性马斯京根模型拥有更多的自由度,在拟合数据时也具有更大的灵活性,从而在河道流量演算过程中数据拟合的更加精准。广义非线性马斯京根方程仍是以连续方程和槽蓄方程为基础进行展开[12]。
连续方程,简化为水量平衡方程见式(6):
式中 t——时间;S——某一河段的储存水量;I——某一河段的来水流量;O——某一河段的出流量。
槽蓄方程如下:
S=K[XI+(1-X)O] (7)
式中 K——蓄流流量关系曲线的坡度,即槽蓄系数;X——流量比重系数,其取值范围为[0,0.3]。
K、X 2个参数数值从某一河段的观测入流量与观测出流量数据中获得。
Chow将水深h与河段的来水流量、出水流量和储存水量建立关系,提出了式(8)—(11):
I=ahn(8)
O=ahn(9)
Sin=bhm(10)
Sout=bhm(11)
式中 a、h、b、m、n——待估计的模型参数;h——水流深度;a、n——某一河段上、下游末端断面流量-水深特征系数;b、m——某一河段平均蓄水深度特征系数;Sin——某一河段上游的存储水量;Sout——某一河段下游末端的存储水量。
将式(8)—(11)联立起来得到式(12)、(13):
由于天然河道(河流)的断面特征与造床流量和输沙能力有关,而天然河道(河流)上、下游的造床流量和输沙能力各不相同,因此Bozorg-Haddad等通过以下方式改变a和n来反映河道(河流)上游和下游段之间形态变化的差异:
式中 a1、n1——某一河段上游断面流量-水深特征系数;a2、n2——某一河段下游斷面流量-水深特征系数。
将式(14)、(15)代入方程S=K[XSin+(1-X)·Sout]β,简化后得到非线性马斯京根模型:
S=K[X(C1Iα1)+(1-X)(C2Oα2)]β(16)
式(16)中,
由于第i和第i+1时段内的存储水量Sin存在一定依赖性,因此Bozorg-Haddad等在考虑了第i和第i+1时段内Sin相互依赖关系的基础上,提出了待优化的广义非线性马斯京根模型:
Sin=K[X1(C1Iiα1)+X2(C1Iα1i+1)+(1-X1-X2)(C2Oiα2)]β(18)
式中 Sin——某一河段第i和第i+1时段内的存储水量;Ii——某一河段第i时段内的来水量;Ii+1——某一河段第i+1时段内的来水量;Oi——某一河段第i时段内的出水量;C1、C2、β、α1、α2、X1、X2、K——待优化参数;C1——α1、n1、m和β的函数;C2——α2、n2、m和β的函数;α1——m和n1的函数;α2——m和n2的函数;β——考虑加权流量与存储水量之间非线性影响的参数;X1——无量纲加权因子,表示某一河段上游流入、流出量对存储水量的相对影响;X2——无量纲加权因子,表示某一河段下游流入、流出量对存储水量的相对影响;K——槽蓄系数。
1.3 适应度函数的确定
步骤一 估计待优化参数C1、C2、β、α1、α2、X1、X2、K。
步骤二 用式(19)计算初始存储水量(S0)。假定初始流出量等于初始流入量(0=I0):
步骤三 用式(20)计算在第i时段内储存水量体积的变化率(ΔSi/Δt):
步骤四 用式(21)计算第i时段内的存储水量:
步骤五 用式(22)计算第i时段内的河段出流量(?i):
步骤六 选取式(23)、(24)作为目标函数来估计广义非线性马斯京根模型参数优化效果:
其中 Oi——第i时段内的实测出流量;?i——第i时段内的演算出流量;SSD——实测出流量与演算出流量差值的平方和;OP——实测流量的峰值;?P——演算流量的峰值;DPO——洪峰误差。
1.4 HHO算法优化广义非线性马斯京根模型参数步骤
步骤一 初始化算法参数。设置最大迭代次数T、哈里斯鹰种群规模N、搜索空间维数d;本文设置最大迭代次数为200,哈里斯鹰种群规模为300,搜索空间维数为8,令当前迭代次数t=0。
步骤二 设定待优化参数C1、C2、β、α1、α2、X1、X2、K的搜寻范围和算法迭代终止条件;文本待优化参数搜寻范围分别设置为C1∈[0,1]、C2∈[0,1]、β∈[0,10]、α1∈[0,10]、α2∈[0,10]、X1∈[0,1]、X2∈[0,1]、K∈[0,1],算法迭代终止条件为当前迭代次数t大于等于最大迭代次数T。
步骤三 确定HHO算法的适应度函数。适应度函数是描述种群个体优劣程度的主要指标,本文选用式(23)、(24)为目标适应度函数。
步骤四 适应度函数计算。计算哈里斯鹰种群中所有个体的适应度值,并确定每只哈里斯鹰的索引位置,与捕食对象适应度值进行比较,若哈里斯鹰个体适应度值优于捕食对象,则以适应度值更优的个体位置作为新的捕食对象位置。
步骤五 利用式(3)—(5)及捕猎行为不断更新哈里斯鹰所处位置,找到目前哈里斯鹰最好索引位置。判断算法是否达到迭代终止条件,若达到终止条件,则转至步骤六,否则重复执行步骤三—四。
步骤六 输出最好哈里斯鹰个体索引位置C1、C2、β、α1、α2、X1、X2、K的值和适应度函数Min.SSD和DPO,算法结束。
2 算法验证
本文选取Sphere函数(式(25))和Ackley函数(式(26))对HHO、PSO[16]和ACO[17]算法进行测试分析,为了使得算法计算结果精度更高,每个函数均连续运行30次。其中,Sphere函数维数为30,搜索范围为[-100,100],Ackley函数维数为30,搜索范围为[-32,32]。设定各个算法的种群大小为50,总的迭代次数为200,分别用HHO、PSO和ACO算法对以上2个函数进行测试,计算结果见表1。
同时,为了验证HHO算法在广义非线性马斯京根模型参数优化中的可行性与有效性,本文用3种算法对广义非线性马斯京根模型参数分别进行了优化,并将其优化后的模型分别应用到洛河宜阳—白马寺段的洪水预报过程中,对比3种算法的Min.SSD和DPO,计算结果见“3.3结果与讨论”部分。
由表1可见,相较于PSO和ACO算法,HHO算法在最优解计算过程中寻优精度更高。
3 实例应用
3.1 研究区域概况
本文研究对象是黄河流域伊洛河水系洛河[18],该河流经河南省境内两大水文站:宜阳水文站和白马寺水文站(图1)。宜阳水文站位于河南省洛阳市宜阳县,介于东经111°45′~112°26′,北纬34°16′~34°42′,属暖温带大陆性季风气候,多年平均气温14.8 ℃,年降水量500~800 mm,多年平均蒸发量1 200 mm;白马寺水文站位于河南省洛阳市白马寺镇,地处东经112°35′,北纬34°43′,属暖温带大陆性季风气候,年均气温12.2~24.6 ℃,年降水量约530~800 mm,年日照约2 200~2 300 h,年均湿度60%~70%。本文基于宜阳水文站和白马寺水文站的实测流量资料,利用哈里斯鹰算法优化广义非线性马斯京根模型的参数。
3.2 数据来源
基于宜阳、白马寺水文站2011年9月18日16时至9月20日20時实测洪水流量资料(表2),利用哈里斯鹰算法、粒子群算法和蚁群算法分别对广义非线性马斯京根模型中的流量演算系数进行优化,并对最终的演算结果精度进行分析评价。
3.3 结果与讨论
a)参数率定。利用3种算法分别对广义非线性马斯京根模型中的参数进行多次优化,得到广义非线性马斯京根模型参数最优优化结果,见表3。
b)参数检验。将广义非线性马斯京根模型参数优化结果带入到式(19)—(24),经多次调试,得到不同算法的最优演算出流过程,见表4;演算结果分析,见表5;以及演算效果,见图2。同时,为了对比不同算法在寻优过程中的效率情况,绘制了迭代收敛曲线图,见图3。
由表4、5可知,HHO算法的最小演算离差值为0,PSO算法和ACO算法的最小演算离差值为1,三者的最小离差值相差很小,但HHO算法的最大演算离差值为14,均小于PSO算法的18和ACO算法的20,HHO算法的平均绝对离差值为5.4,均小于PSO算法的9.3和ACO算法的10.1,因此,从演算离差值角度来看,HHO算法均优于PSO算法和ACO算法,说明HHO算法具有良好的优化性能。
由表5和图2可知,HHO算法的Min.SSD值为1 237,均优于PSO算法的3 112和ACO算法的3 533,特别是洪峰位置处,HHO算法的演算流量与实测流量最为接近,误差DPO仅为5,均优于PSO算法的14和ACO算法的17,且峰现时间基本一致。
从图3可以看出,HHO算法收敛速度最快,在迭代次数不到60时便达到了最优值,且计算精度高于其他几种算法。
故证明基于哈里斯鹰算法的广义非线性马斯京根模型在洛河宜阳—白马寺段的流量演算效果更为精准,因此,本文研究结果适合应用于洛河宜阳—白马寺段的洪水预报工作。

