基于局部观测数据的一维热传导方程系数与初值同时反演问题的数值计算

陈振兴，万广红，阮周生

（东华理工大学理学院，江西，南昌 330013）

0 问题介绍

热传导方程是一类用来刻画物质内部热传导过程的基本方程，它在材料科学、物理学和工程学等领域中有着重要的应用。在众多实际应用中，由于测量技术或实验手段的限制，往往需要通过间接的测量数据来反推热扩散系统中的未知参数或函数，数学上将该类问题称为热传导方程反问题。逆时反问题是热传导方程反问题研究的热点之一，已有学者进行了相关研究。文献[1]通过变量替换，将一维热传导初值反问题转化为一维Hausdorff 矩问题，基于该矩问题的条件稳定性获得热传导初值反问题的条件稳定性。文献[2-4]利用拟边值正则化方法研究了热传导逆时反问题，其中文献[2]提出一种求解热传导逆时反问题的修正拟边值正则化方法，分析了该正则化方法对应正则化解的收敛率，并借助有限元插值技术，设计出易于并行的反演算法；文献[3]基于拟边值正则化方法研究了热传导方程逆时反问题，证明了正则化解的先验和后验收敛率，给出了基于边界元法的数值结果；文献[4]将逆时反问题转为Tikhonov 正则优化问题，在最优控制框架下推导了优化问题的一阶必要性条件，并在最优控制框架下分析了最优控制问题与几类拟边值正则化方法的内在关联，为求解逆问题提供了更一般的框架。文献[5]利用解析延拓技术证明了基于稀疏数据热传导方程初值反问题的唯一性，借助有限元方法对逆问题进行离散化，结合离散Tikhonov 正则化和广义交叉验证准则获得初始值的稳定数值逼近。文献[6]基于终止时刻有限点的瞬态温度观测，借助再生核方法和Tikhonov 正则化方法提出了一种求解逆向热传导问题的数值方法。文献[7]扩展了一种半监督深度神经网络方法，并将其应用于热传导方程逆时反问题的数值计算上，通过数值算例验证了该方法的有效性。文献[8]提出了一种空间滤波技术——四阶紧致滤波求解热传导方程逆时反问题，理论上分析了该紧致滤波法求解逆时反问题的收敛率。文献[9]利用截断奇异值正则化方法研究一类扩散系数为时间变量函数的热传导方程逆时反问题，并给出了截断奇异值正则化解的后验收敛率估计。文献[10]基于热方程基本解，利用边值积分方程法和Tikhonov 正则化方法构造了求解二维热传导逆时反问题的数值反演方法。Raissi 等[11]提出物理信息神经网络PⅠNN（Physics-Ⅰnformed Neural Networks）用于逼近偏微分方程中待求的未知函数。该方法利用深度神经网络超强的函数拟合能力，通过优化方程对应的最小二乘拟合函数和初边值条件对应的最小二乘拟合函数，指导可调参数(权重和偏置)的迭代更新过程，最终得到微分方程定解问题的神经网络逼近模型。文献[11-13,16]等采用深度神经网络求解热传导方程正反问题，得到理想的逼近效果。文献[17-18]分别使用多项式特解、临界点理论中的山路引理对稳态热传导方程进行求解。文献[19]利用线性叠加原理及有限元插值技术，探讨一类带第二类边界条件一维热传导方程逆时问题。

基于现实情况的考虑，观测数据往往更容易在局部区域内测量得到，本研究基于局部观测数据下一维热传导方程系数和初值，同时反演问题的唯一性理论及其基于深度学习的数值反演算法。即考虑如下问题

1 同时反演问题的唯一性

下面利用函数代换及热传导问题解的解析延拓性，证明同时反演问题的唯一性，结论表述如下。

局部观测值变为

当A被确定后，可得观测值v（x,T1） =g（x）e-AT1，x∈ (0,l)，由文献[15]第44 页结论知，当φ(x)∈H2(0,l) ∩H(0,l)，问题(1)中的初值φ（x），也即问题(2)中的初值φ（x）可由终止数据v（x,T1）唯一地决定。证毕。

2 反问题PⅠNN 反演算法

物理信息神经网络(PⅠNN)求解偏微分方程的基本思想：构建深度神经网络函数n（x,t;θ）近似偏微分方程问题的解u，将偏微分方程定解问题的数值求解转化为基于神经网络函数n（x,t;θ）的约束优化问题。

由于问题(1)与问题(2)等价性，将(1)中的同时反演问题转为问题(2)中的同时反演问题。基于u(x,t)的观测条件，下面推导v(x,t)的观测条件。

由式(4)可知

又因为v（x,T） =g（x）e-AT1，故得到问题(2)的

1观测约束条件为

依据PⅠNN 算法思想，建立问题(2)中对应的偏微分方程残差网络

显然fv的值越趋近于0，表示神经网络的预测值越符合物理模型。类似方程残差网络，建立定解条件的残差网络，在本算法中，将观测约束视为微分方程的定解条件，故得到下面定解条件残差网络

在网络训练优化过程中，PⅠNN 通过优化算法使得方程与定解条件残差网络在采样点处的平方误差之和达到极小来优化神经网络中的参数θ，在满足一定精度要求的前提下，得到微分方程定解问题解v（x,t）的神经网络逼近函数n（x,t;θ）。因此可知用于优化的损失函数Loss由以下3 部分组成

其中MSEf，MSEb，MSEo分别定义为

通过最小化损失函数Loss，PⅠNN 能利用神经网络的函数拟合能力得到函数v(x,t)的近似解n（x,t;θ），即v(x,t) ≈n（x,t;θ），进而可得同时反演问题的近似解。综上所述，可以归结反演问题的反演算法如下：

反演算法

step2：构建深度神经网络n（x,t;θ）作为精确解v（x,t）的近似值，初始化网络参数θ，即网络的权重w和偏置b；

step3：定义热传导方程残差网络(10)和约束条件残差网络(11)；

step5：利用Adam 优化器对损失函数Loss参数进行更新，判断Loss是否小于理想误差，如果小于理想误差，停止训练，得到网络；否则继续训练网络，直至Loss小于理想误差，找到满足精度要求v（x,t）的神经网络近似解n（x,t;θ）；

step6：由(8)及φ(x) ≈n（x,0;θ）得到同时反演问题的数值解。

3 数值算例

本部分通过数值算例来验证方法的有效性，

算例2设精确的初始函数和零阶项系数分别为φ（x） = 10sinπx+x（1 -x），A= 10，对应的定解问题(1)的精确解无解析表达式。不同局部区域观测数据和噪声下同时反演的系数和初值数值解见表1 和图5-8。

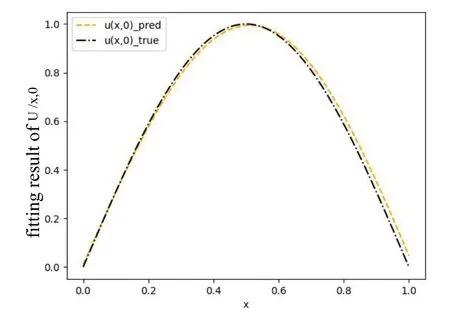
图1 算例1δ =0.1%，[l1 , l 2] = [,]的反演结果Fig.1 Ⅰnversion result of example 1 withδ =0.1%,[l1 , l 2] =[

图2 算例1δ =1%，[l1 , l 2] = [,的反演结果Fig.2 Ⅰnversion result of example 1 withδ =1%,[l1 , l 2] =

图3 算例1δ =0.1%，[l1 , l 2] = [,]的反演结果Fig.3 Ⅰnversion result of example 1 withδ =0.1%,[l1 , l 2] =[]

图4 算例1δ =1%，[l1 , l 2] = [,]的反演结果Fig.4 Ⅰnversion result of example 1 withδ =1%,[l1 , l 2] =[]

图5 算例2δ =0.1%，[l1 , l 2] = [的反演结果Fig.5 Ⅰnversion result of example 2 withδ =0.1%,[l1 , l 2] =[

图6 算例2δ =1%，[l1 , l 2] = [,]的反演结果Fig.6 Ⅰnversion result of example 2 withδ =1%,[l1 , l 2] =[,]

图7 算例2δ =0.1%，[l1 , l 2] = [,]的反演结果Fig.7 Ⅰnversion result of example 2 withδ =0.1%,[l1 , l 2] =,]

图8 算例2δ =1%，[l1 , l 2] = [ ,]的反演结果Fig.8 Ⅰnversion result of example 2 withδ =1%,[l1 , l 2] =[,]

表1 不同观测噪声水平下系数与初值反演的结果Table 1 Ⅰnversion results of coefficient and initial values under different observed noise levels

从反演结果可以看出，当观察数据的噪声水平逐渐降低时，反演结果越来越靠近精确解，体现出基于PⅠNN 的同时反演算法是稳定的，且在观测区域内等距采样点数目相等的情况下，相对较大的观测区间对应的反演结果越靠近精确解，由于观测点越近，观测数据的线性相关性越高，这说明相关性较弱的采样数据能更能较好地用于本算法的计算。

4 小结

本研究探讨了热传导方程系数和初值同时反演问题，基于终止时刻的局部观测数据及时空一点观测数据，通过解析延拓法及函数代换证明了系数和初值同时反演问题的唯一性，并设计了同时反演问题的PⅠNN 算法，通过数值算例验证了反演算法的有效性和稳定性。相较于参考文献里研究的逆时反问题，本研究从理论上建立了基于局部观测数据的同时反演问题的唯一性理论，并从算法上给出了基于神经网络的无网格化反演算法，使论文研究成果在实际应用中更具有参考价值。