鲸鱼算法优化VMD-CNN 在滚动轴承故障诊断中的应用

李 萌，张 强

（长春大学 机械与车辆工程，吉林 长春 130022）

0 引言

轴承在制作生产过程中存在制作误差、安装不当、交变载荷等因素易造成轴承损伤。滚动轴承一旦发生故障轻则设备产生异常振动与噪声，重则设备损坏乃至发生重大灾难性事故[1]。因此，轴承故障诊断具有极为重要的意义。

轴承故障特征提取时易受到噪声影响，各位学者提出了各种信号分解理论。如Huang 等[2]提出经验模态分解（Empirical Mode Decomposition，EMD），能够在噪声条件下自适应分解原始信号并提取有效信号特征，但此方法存在模态混叠与端点效应问题。Dragomiretskiy 等[3]提出变分模态（Variational Mode Decomposition，VMD）算法理论，可以有效避免端点效应、抑制模态混叠。陈桂平等[4]采用VMD 对滚动轴承进行信号分解，因VMD 算法其惩罚因子和分解层数难以确定，故信号分解会产生一些虚假分量，并影响后续故障分类精度。刘伟等[5]提出一维卷积神经网络（One-Dimensional Convolutional Neural Network，1DCNN）对原始振动信号进行智能诊断，未考虑原始信号包含太多冗余信息。

针对以上问题，提出基于鲸鱼优化算法（Whale Optimization Algorithm，WOA）优化VMD 参数与CNN算法相结合的滚动轴承故障诊断方法。利用提出的WOA-VMD 算法对原始信号分解，并且利用连续小波变换将优选本征模量（Intrinsic Modulus Function，IMF）的一维时序图转化为相应时频图，再通过搭建的卷积神经网络进行特征提取与故障诊断。

1 鲸鱼算法优化变分模态分解和卷积神经网络故障诊断

使用鲸鱼算法优化变分模态并经过卷积神经网络进行故障诊断。首先，原始信号经WOA-VMD 算法分解得到若干IMF，筛选后进一步提取近似熵作为特征向量，优选特征最突出的IMF；其次，使用连续小波变换获取最优IMF 的时频图；最后，引入CNN 模型实现轴承故障图像模式识别。WOA-VMD-CNN 故障诊断流程如图1 所示，具体步骤如下：

图1 WOA-VMD-CNN 的故障诊断流程

（1）利用WOA 优化VMD 算法参数k、alpha；

（2）利用步骤（1）获得的最佳参数对原始数据进行分解得到IMF；

（3）得到本征模量之后利用近似熵对IMF 进行优选；

（4）将优选的IMF 进行连续小波变换，将时序信号转化为二维时频图，以便CNN 进行特征提取与故障分类；

（5）将转化为二维时频图的特征图划分为训练集、验证集和测试集；

（6）将划分好的训练集输入到CNN 模型中，训练好模型的参数；

（7）最后，将验证集与测试集输入到已经训练好的CNN 模型中，对模型性能进行验证。

2 实验验证

2.1 实验数据

实验数据选取凯斯西储大学标准轴承故障数据集（CWRU）[6]，由驱动电机、扭矩传感器、工控机、测功机、风扇端轴承、驱动端轴承组成。电机负载选取0 Hp，转速1797 r/min，采样频率12 kHz，轴承状态分为：正常状态、滚动体故障、内圈故障、外圈故障，轴承故障直径分别为：0.007 mm、0.014 mm、0.021 mm，根据轴承不同损伤位置与损伤直径，可分为9 类不同故障。

2.2 实验结果与分析

利用WOA 算法对VMD 算法的分解层数与惩罚因子alpha进行自主寻优。通过重采样对原始数据进行切分扩展，得到3000 样本，每个样本取1024 个点，WOA 算法中选取最小包络熵作为适应度函数。WOA算法初始化参数：种群数量50、迭代次数20、维度2的取值范围[2，8]，alpha的取值范围[500，5000]。由其适应度函数在迭代第二次开始收敛，其最佳适应度函数值为0.00033475，此时k的最优值为4，alpha的最优值2932。

原始轴承振动信号经WOA 优化VMD 分解，自适应寻找VMD 算法的最优核心参数组合，图2 为WOA 优化VMD 信号分解之后得到的4 个IMF 时域图，每个IMF 都对应一个中心频率和围绕中心频率附近窄宽带信号。图3 为对应IMF 分量的频谱图，各个IMF 中心频率，IMF1 在200 Hz 左右，IMF2 在1000 Hz 左右，IMF3 在2000 Hz 左右，IMF4 在800 Hz左右。各个IMF 中心频率相互独立，能够有效避免模态混叠问题，原始信号的频率近似可以由这4 个分量的频率叠加而成。VMD 没有采用极值包络线递归的方式求取IMF，故能得到较单纯的模态分量。

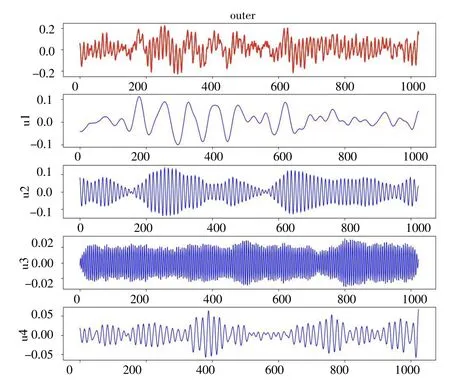
图2 WOA 优化的VMD 的信号分解

图3 对应分量的频谱

分别计算4 个IMF 的近似熵，并对IMF 进行优选，其近似熵见表1。由于近似熵是用来描述振动信号的不规则性及复杂程度，信号产生新模式的概率越大，复杂性就越大，相对应的近似熵也随之增大，由表1 可知IMF4 的熵值最大，故选取IMF4 作为新数据选取故障特征。

表1 各IMF 近似熵值

对选取的IMF4 进行连续小波变换，将时序信号转化为二维时频图，方便CNN 模型对故障特征进行提取与分类。将已分组的训练集输入到定义的CNN网络模型中进行训练，计算损失函数与更新网络结构参数，WOA-VMD-CNN 模型选取交叉熵函数作为损失函数，采用梯度下降法最小化损失函数并对其求导更新权重与偏置。当模型训练好之后，输入验证集，测试模型的稳定性。图4 结果显示，训练集与测试集的故障诊断分类准确率曲线基本吻合，且在第50 次迭代时，分类准确率函数开始收敛，该模型故障分类准确率为99.78%。表明该模型参数设置合理，训练充分，具有一定深度，WOA-VMD-CNN 能高效提取故障特征，避免信号过分解与欠分解，并且利用连续小波变换将一维时序图转化为二维时频图，卷积神经网络更容易提取其特征信息。

图4 WOA-VMD-CNN 分类准确率

2.3 不同算法对比

将WOA-VMD-CCN 方法与CNN、VMD-CNN 算法进行对比分析。选取凯斯西储大学0Hp 下10 种工况的轴承数据，每种工况采集122571 个点，共3000个样本，每个样本1024 个点。3 种方法的CNN 网络参数参照见表1。对3 种方法进行故障诊断准确率对比，各算法的识别准确率见表2。

表2 各算法准确率对比

从表2 中知，采用CNN 模型对原始轴承振动信号数据进行提取特征，其准确率为87.65%，因为在噪声的环境下，CNN 会误提取一些特征，从而导致分类准确率略低于其他两种模型；VMD-CNN 模型准确率为95.28%，VMD-CNN 模型先将实验数据进行变分模态分解，在通过卷积网络提取特征以及智能诊断，VMD 分解虽然可以去除一些噪声，但是VMD 参数难以确定，易导致信号过分解或欠分解使得故障分类准确率下降。WOA-VMD-CNN 模型准确率为99.78%，诊断效果好，方法有效。

3 结语

采用鲸鱼算法优化变分模态分解，自适应寻找VMD 算法的最优核心参数组合，克服了信号过分解与欠分解的问题。使用连续小波变换获取了最优本征模量的时频图。引入CNN 模型实现了轴承故障图像模式识别。提出的WOA-VMD-CNN 方法综合了鲸鱼算法全局快速寻优、VMD 自适应分解和CNN 提取数据特征与分类能力，有效提高了故障识别精准率，与CNN、VMD-CNN 两种方法对比，WOA-VMD-CNN 方法的故障诊断率最高。