内河船舶尾气监测的多无人机路径规划研究

王广生，孙祎峥，孙海军，鱼 童，张 铖，周云鹏

（1.中国港湾工程有限责任公司，北京 100027；2.河海大学港口海岸与近海工程学院，江苏南京 210098）

引言

近年来，尽管国际海事组织（IMO）及各国政府通过降低船用燃料油中的硫含量来控制船舶大气污染物排放，但由于高、低硫油价格存在较大差距，低硫油高昂的使用成本使得高硫燃油使用的违规率依然较高。为解决此问题，已有众多研究尝试通过移动式监测系统[1]、岸基遥感监测[2]、无人机嗅探检测[3]等方式开展船舶尾气污染防治工作。其中，无人机嗅探检测方式凭借在机动性强和执法效率高等优势，受到了行业内学者的广泛关注，在海事管理领域的可行性得到了充分的证明[4-6]。

然而，在船舶流量密度较大的情况下，仅依靠人工操控无人机完成检测工作效率低、危险性也较高，因此研究续航时间有限的条件下，多无人机协同是实现无人机自动化监测的关键问题。

多无人机协同类属于任务分配问题[7]，即在已知无人机数量和任务数量的条件下，考虑到环境威胁、无人机的续航能力、载荷能力约束以及任务的特殊需求，进行合理的任务分配，使得各无人机均能够以最优效率协同完成工作。路径寻优问题一般可将其归为经典的旅行商问题[8]，多无人机协同的情景涉及到多旅行商问题（Multiple Traveling Salesman Problem,MTSP）和移动目标旅行商问题（Moving Target Traveling Salesman Problem,MTTSP）。针对MTSP 问题，目前主要采用启发式算法进行求解，如杂草入侵算法[9]、人工蜂群算 法[10]、遗传算法[11]、粒子群算法[12]等。例如，Bourjolly等[13]建立了具有时间相关性的MTTSP 问题模型，并使用禁忌搜索算法求解航天器在轨服务问题；Moraes 等[14]通过对比遗传算法、蚁群算法、模拟退火算法在解决MTTSP 时的表现，得出遗传算法在求解质量和求解效率等方面表现最佳。

本文基于MTTSP 和MTSP 模型，构建了多无人机巡检路径规划模型（Multiple UAVs’ Path Planning,MUPP）。针对多无人机巡检任务分配的需求，提出两阶段算法（Two Phase Algorithm,TPA）以提升算法的求解性能，并以长江干线航道断面为例进行仿真，验证模型的科学性和算法的有效性。

1 模型构建

1.1 模型假设

为了将实际问题理论化，便于模型构建，需对模型做出以下假设：

1）无人机前往检测时的速度恒定且快于船舶；在检测时间内，船舶按当前速度和航向行驶；无人机到达目标点后能够完成船舶燃油品质的检测；

2）无人机跟随检测时的速度与被检测船舶速度一致，检测所需时间不随船舶变化；

3）旋翼无人机不同于固定翼无人机，其转弯半径较小，故不考虑最小转弯半径约束；不考虑飞行过程中威胁、地形和气候等因素的影响。

1.2 模型建立

基于上述假设，多无人机巡检路径规划（Multiple UAVs’ Path Planning,MUPP）问题的表达如下：

式中：

L—巡航路径总长度；

K—无人机的集合；

M—无人机的数量；

dij—船舶si与船舶sj的距离；

T—检测总时间；

Q—无人机续航能力；

式（1）为目标函数，表示优化的目的为多无人机总飞行长度最小。约束条件（2）表示对巡检总时间T 进行限制。约束条件（3）表示每艘船舶仅能被一架无人机检测一次。约束条件（4）、（5）表示路径中每个船舶只能分别与两个船舶相连，保证路径的连续性。

1.3 数据准备

MUPP 模型中的L、T值按照图1 方法计算，图中tr、dr为无人机返回基站的时间和距离；tj为无人机飞往船舶的时间；td为无人机跟随检测的时间；vd为无人机速度；vH(i)为船舶H(i)的速度；tH(i)为检测时间；dH(i)为飞行距离。

图1 无人机飞行总长度和时间的计算方法Fig.1 Calculation method of total flight length and time of UAVs

其中，飞行时间tf的计算原理为：已知无人机检测完H(i)船后的位置D 点坐标为(x1,y1)，待检船舶H(j)位置O 点坐标为(x2,y2)。以(x2,y2)为原点，H(j)船舶航行方向为y 轴建立直角坐标系，船舶H(j)匀速前行至检测点M 后，无人机飞行方向与y 轴夹角为θ，得到方程式（6），化简可得飞行时间tf的计算式（7）。计算简图如图2 所示。

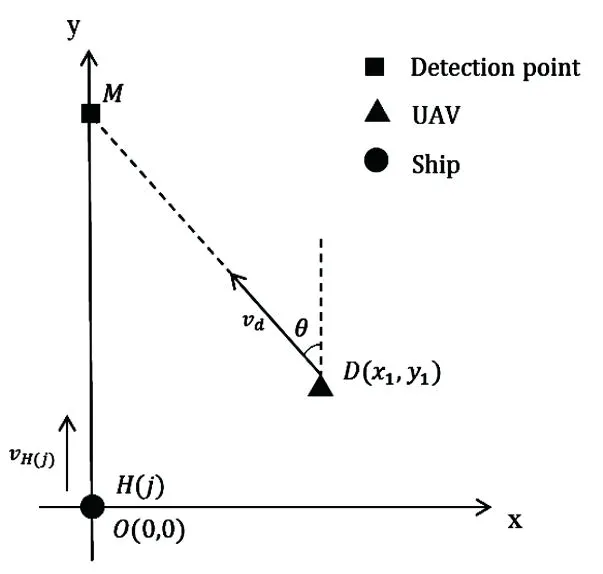
图2 飞行时间计算示意图Fig.2 Schematic diagram of flight time calculation

1.4 模型求解

MUPP 模型中的路径规划问题属于NP-hard 问题，本文采用融合了遗传算法（GA）和模拟退火算法（SA）两种算法的混合模拟退火遗传算法[15]（Simulated Annealing Genetic Algorithm,SAGA）作为基本算法。该改进遗传算法同时具有遗传算法的全局搜索特性和模拟退火算法的局部搜索特性。

此外，由于MUPP 模型需要多无人机协同完成巡检任务，故涉及到任务分配的问题。基于改进的聚类算法，将该任务分配问题抽象为MTSP 后，再将MTSP 转化为多个TSP 进行求解。

考虑到船舶运动特点及无人机任务分配的均衡，在上下行船舶数量较为接近的条件下，提出一种基于上下行船舶分组和任务均分的K-means++算法。其主要思想为将船舶数据集分为上下行两组数据集，再引入容量限制要求，使得聚类形成的集合中船舶数量较为均匀。GT-K-means++算法的具体步骤如下：

设V=｛v1|i=1,2,…,n｝表示待检测船舶节点集，初始簇集为s=(c1,c2,…,cj,…,ck)，k 为类簇数量。初始类簇cj的中心为μj,j=1,2,…,k，每个类簇中节点的个数qj=0。

1）根据船舶航向数据，将船舶节点集分为上行船舶节点集Vup和下行船舶节点集Vdown；接着初始化类簇容量，即每个类簇中船舶数量上限为Q=ceil(n/k)。

2）对上行船舶节点集Vup，初始聚类中心是该集合中随机选取的一个船舶点；用最短距离D(x)表示每个船舶点与已有聚类中心之间的距离，然后用轮盘赌法选出下个聚类中心点；重复以上操作，直到选出上行船舶的kup个聚类中心点。

3）对下行船舶节点集Vdown，按照步骤2 中的方法选出下行船舶的kdown个聚类中心点。

4）针对各上行船舶点vi∊Vup，按照公式（8）计算各船舶点vi到其类簇中心μj的欧几里得距离ρ(vi,μj)。

接着将所有船舶点按照距离值从小到大排序。

5）聚类。取到类簇中心μj距离值最小的船舶点vi，并令qj=qj+1，判断类簇cj当前船舶点个数是否满足qj≤Q。若满足，则将该船舶点vi分配给类簇cj；若不满足，则将该船舶点vi到类簇cj的距离值设为无穷大，重新排序并分配下一船舶点，直到分配完所有船舶点。

6）根据公式更新聚类中心点jμ的坐标，类簇cj中船舶点数量是，若其中心点坐标没有发生变化，则聚类完成收敛，输出聚类结果；否则，转4）。

7）针对各下行船舶点vi∊Vdown，按照4）至 6）的方法完成聚类，并输出聚类结果。

综上，本文采用了GT-K-means++算法对水域内待检测船舶点进行聚类，将船舶分成多个子集后，运用SAGA 对每一个船舶子集进行无人机巡检路径规划，从而构成“GT-K-means++”+“SAGA”的二阶段算法（Two Phase Algorithm,TPA），以此来分段求解MUPP。

2 实验分析

2.1 研究范围

本文选择中国长三角船舶排放控制区范围内长江干线航道南京段进行仿真实验（如图3 所示），并作参数影响分析。研究范围中顶点经纬度为：32.25241 °N，119.156 °E；32.23642 °N，119.22114 °E；32.21797 °N，119.21249 °E；32.2372 °N，119.15147 °E。研究范围的断面长度约4 km，宽度约1.3 km。船舶航行数据均源自中国交通运输部海事局的AIS 信息服务平台。图中圆形点表示设定的无人机基站位置，黑色线段为航道边界线，船形标志表示船舶分布位置。

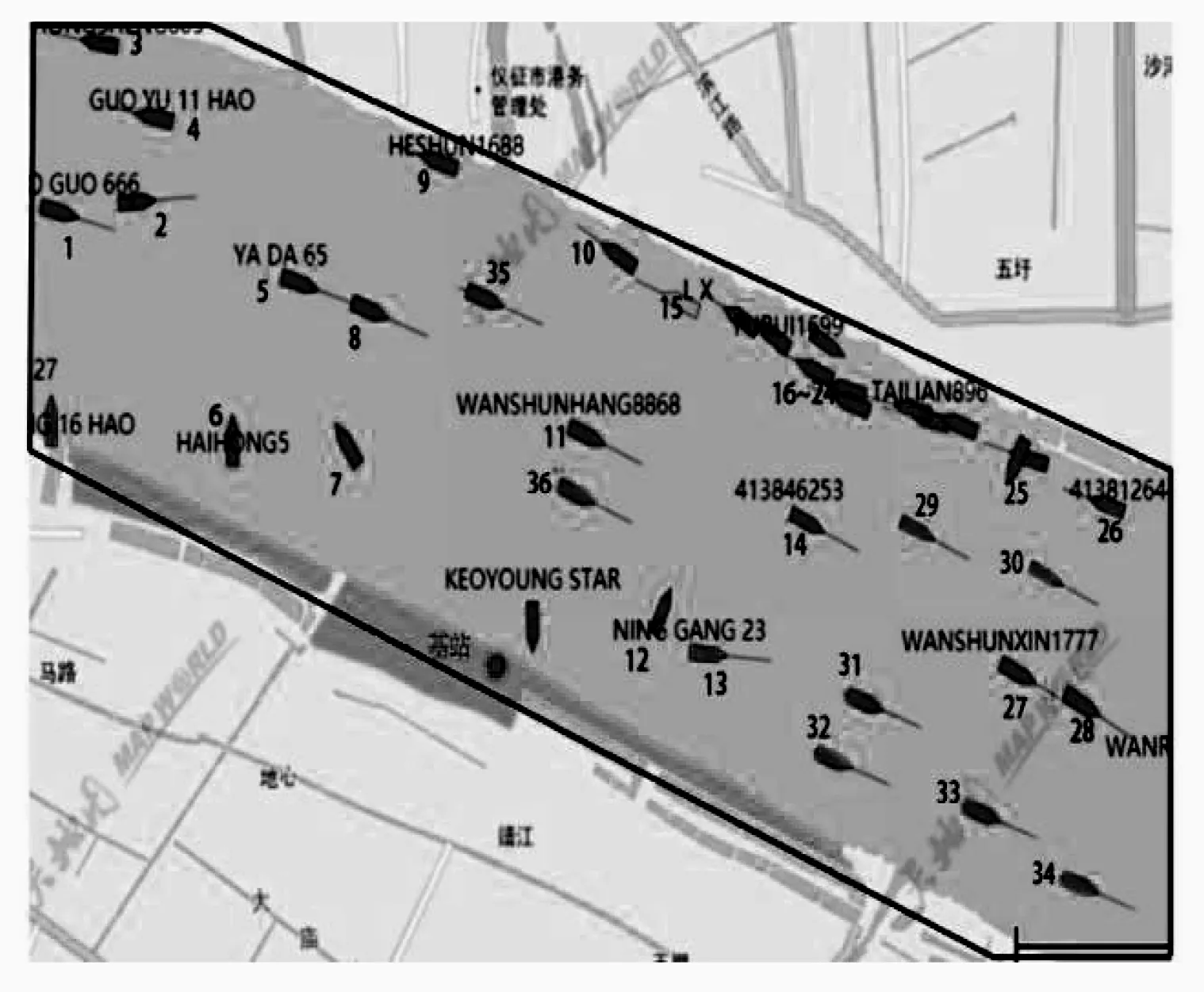
图3 基于AIS 的研究范围和船舶实时位置Fig.3 The research scope based on AIS and the real-time positions of the ships

2.2 仿真结果分析

算法采用Python 语言编写，相关参数与模型参数设置如表1 所示，结合船舶AIS 航行数据，给范围内所有船舶设定相应的编号、速度以及坐标。

表1 仿真参数设置Tab.1 Simulation parameter settings

TPA 算法迭代收敛图如图4 所示，从迭代结果可知，约350 次后收敛，表2 为使用TPA 算法运算得到的各无人机的巡检路径及所需时间。计算结果显示，各无人机的任务量均为9，各无人机巡检时间平均值19.5 min，方差为1.57，任务量较为接近，且满足无人机的续航时间要求，四架无人机可均衡、高效地完成巡检工作。

表2 巡航路径和时间Tab.2 Cruise path and tim

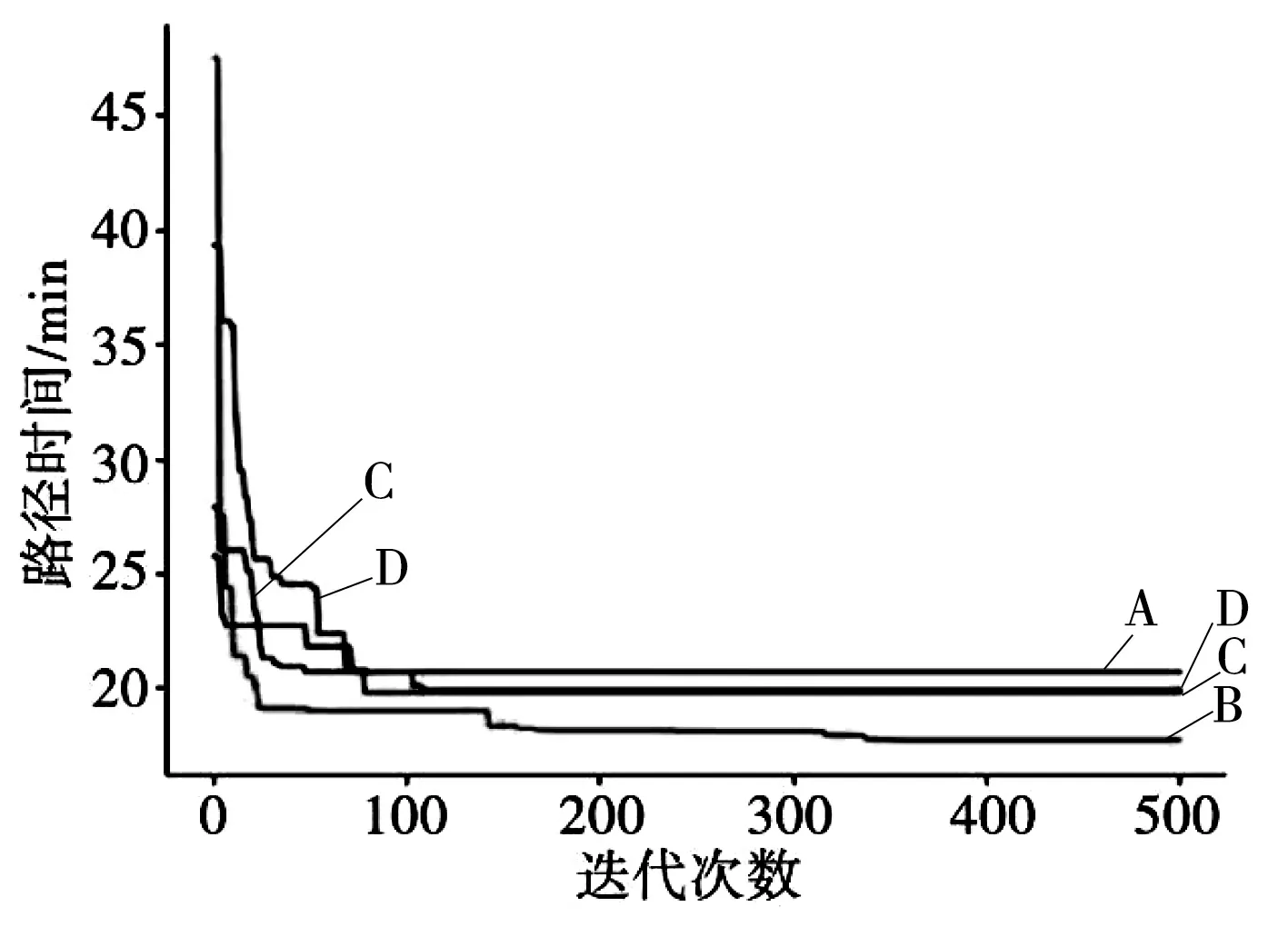
图4 TPA 迭代结果Fig.4 TPA iteration results

2.3 模型参数影响分析

1）船舶数量及无人机数量对TPA 结果的影响

假设各无人机速度vd均为20 m/s，单船检测时间td为3 s。分别在不同场景下运行10 次程序，得到最优的路径总时间T，如表3 所示。结果显示当船舶数量大于60 艘时，出现2 艘无人机无法满足巡检要求的情况，并随着船舶数量的增加，所需无人机数量不断增加，当船舶数量达到100 艘时，需4 台无人机才能完成巡检任务。

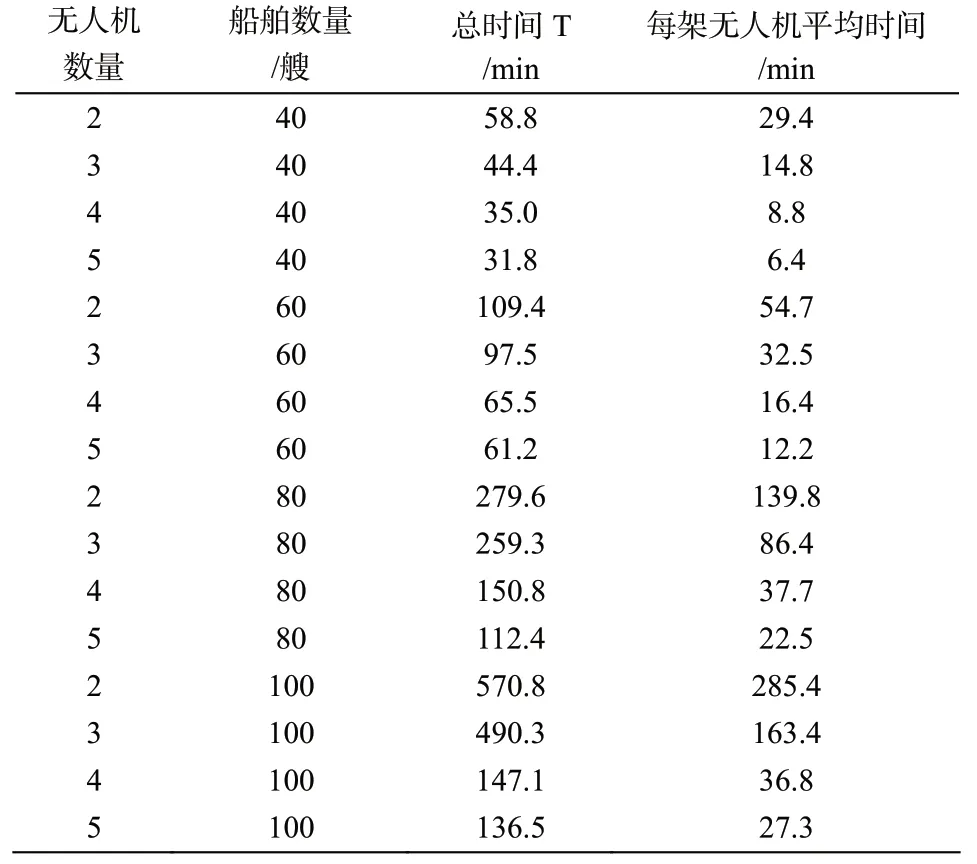
表3 16 种场景下的最优路径时间Tab.3 Optimal path time under 16 scenarios

可以发现，随着船舶数量的增加，无人机巡检总时间T 也呈增长趋势。虽然场景15 中船舶数量比场景11 中多20 艘，其总时间T 却比场景11 少3.7 min，表明船舶数量是影响巡检路径时间的主要因素。当航道中船舶数量为40 艘时，配备两架续航时间为40 min 的无人机即可满足巡检要求；当船舶数量为60 艘时，应配备3 架续航时间为40 min的无人机或2 架续航时间为60 min 的无人机；而对于待检测船舶数量较多的情况（80 艘、100 艘），则需要配备4 台续航时间为40 min 的无人机才能够顺利完成巡检任务。

当船舶数量为60 和船舶数量为100 时，无人机数量对巡检时间如图5 所示。图中方形、圆形线段为两种场景下T 值的变化曲线，三角形线段为每增加一架无人机时T 值下降率的变化曲线。

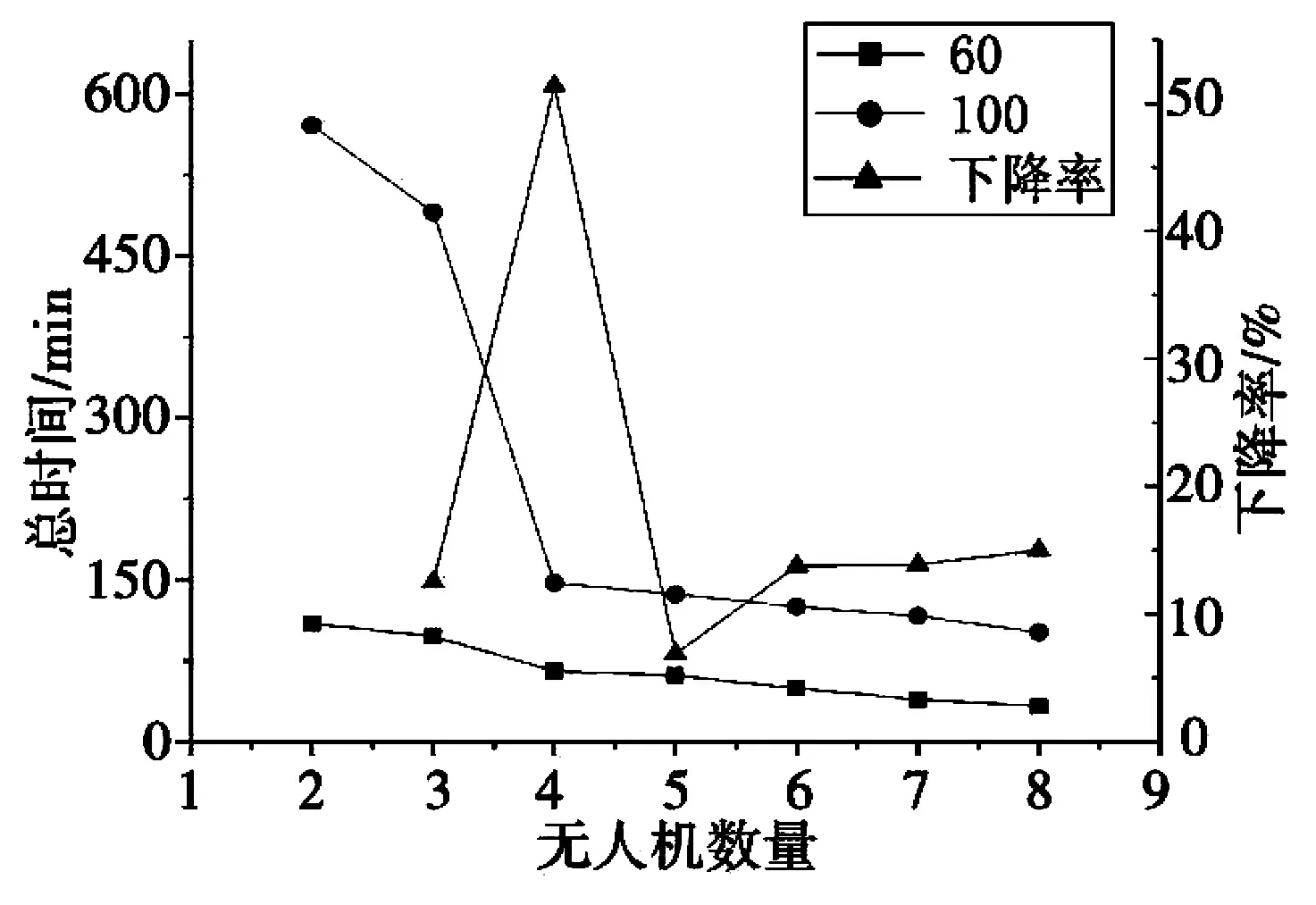
图5 不同无人机数量下的总巡检时间Fig.5 Total inspection time under different numbers of UAVs

从图5 可以看出，无人机数量的增加会减少巡检路径总时间，当无人机数量由3 增加至4 时，T值下降率约51 %，变化最为显著，而在无人机数量由4 增加至8 时，T 值下降率保持在14 %左右，巡检效率提升不算明显。由于内河航道中船舶流量有明显的高峰期与低谷期，配备2 架或3 架无人机不能够满足较多船舶数量情况的巡检需求，故每个无人机基站配备4 台无人机最为合理。

2）船舶速度和无人机速度对TPA 计算结果的影响

以场景15 为例，在vd为14、18、22、26、30 m/s的五种情景下，分别求出td为3、6、9、12 s 时的路径总时间T，实验结果如图6 所示。

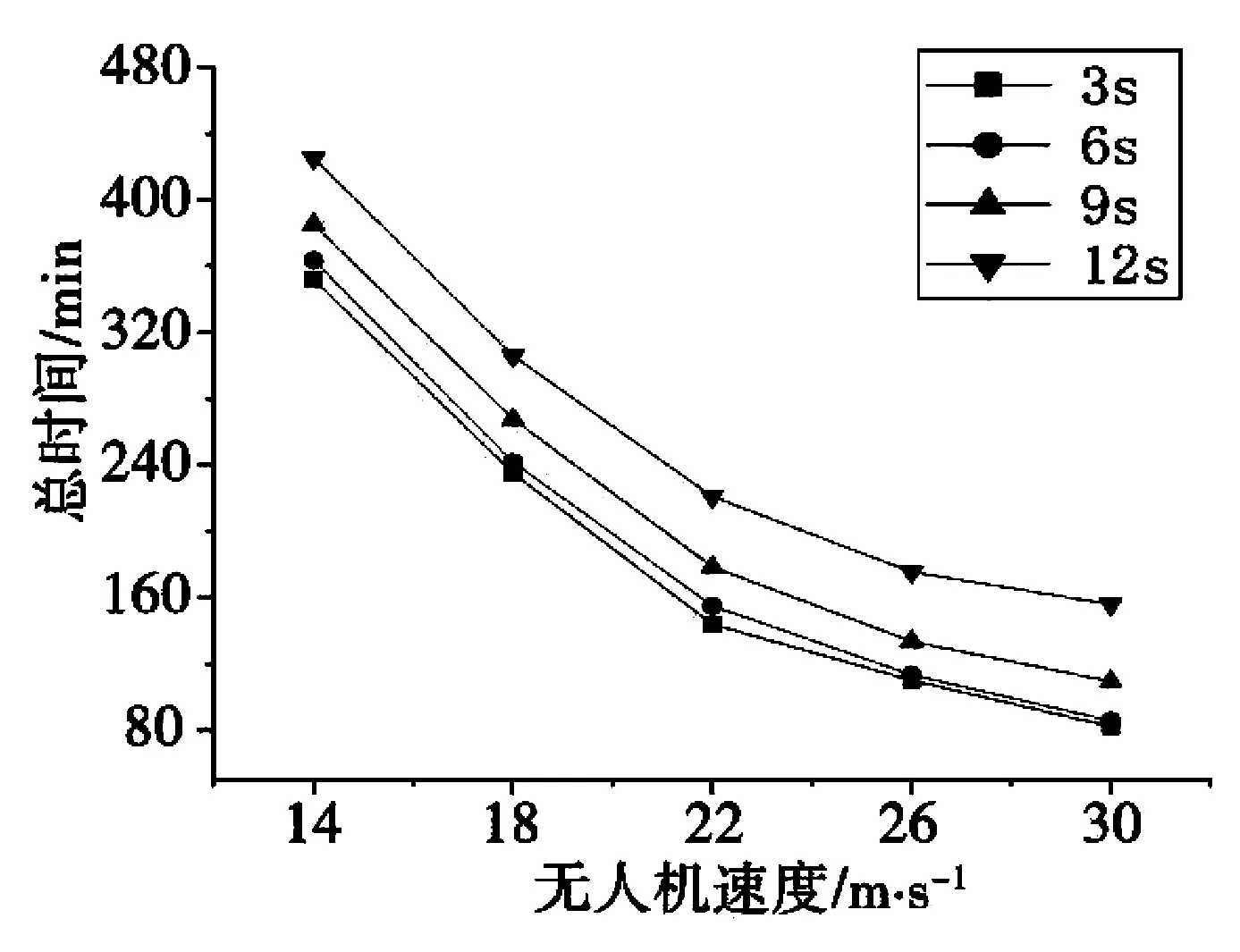
图6 不同飞行速度下的总检测时间Fig.6 Total detection time at different flight speeds

图6 显示，在vd相同的情况下，td每增加3秒，T 值也随之增长，从3 s 增长至6 s 时，T 值增长量较小，约6 分钟；从6 s 增长至9 s 时，T 值的增长量约23 分钟；从9 s 增长至12 s 时，T 值的增长量更多，约42 分钟。可见td的增加表示无人机跟随检测所需长时间的增加，同时由于其他船舶行驶得更远，也会导致巡检时间的延长。当td保持不变时，随着vd的增加，T 值逐渐减小，这是由于飞行速度提高导致检测间隙时间缩短所致；此外，在vd由14 m/s 增加至22 m/s 的过程中T 值缩减幅度较大，但随着vd值的继续增加，T 值缩减幅度呈现逐渐减小趋势。综上分析，为提高巡检效率，建议执法部门选用速度22 m/s 的无人机，并选配检测设备响应时间小于6 s 的检测仪来完成巡检工作。

3 结语

为解决内河船舶尾气排放监测工作中无人机自动化巡检的部署方案问题，本文以无人机总飞行长度最小化为目标函数，提出了一种多无人机动态路径规划模型（MUPP），并采用“GT-K-means++” +“SAGA”的二阶段算法（TPA）对这一NP-hard 问题进行求解。以长三角船舶排放控制区范围内长江干线航道南京段为例，基于实时AIS 船舶航行数据，利用TPA 算法进行实例分析，结果显示：待检船舶数量的增多会对无人机的数量及续航时长有更高的要求，考虑到航道巡检需求、无人机的巡检效率，每个基站配备4 台速度为22 m/s 的无人机，搭载检测耗时少于6 s 的高性能检测仪器较为合理。