新型数控机械加工进刀工艺探究

万端威

（杭州航天电子技术有限公司，浙江杭州 311400）

0 引言

在数控机械的实际应用过程中，对进刀工艺参数进行精准确定，是确保加工质量的关键环节。特别是在一些特殊的精密零件加工中，通常涉及进刀工艺参数的优化改进，因此需要对此问题展开深入探究。

1 案例概况

某厂主要生产涡轮发动机所需的叶盘器件（图1）。为提升涡轮发动机的整体性能，其叶片部件采用复杂空间自由曲面模式，对叶片的压力面与吸力面进行设计。在这种设计模式下，叶盘的结构与形状均具有较高的复杂度，且叶片厚度较低，承受的弯扭也相对较高，进而导致相邻叶片之间存在较窄且较深的通道。基于叶盘的上述特点，其对于数控加工的要求也相对较高。结合以往的生产经验可知，基于以往的进刀工艺参数，叶盘的加工效率相对偏低，且刀具磨损速度较快，带来了较高的额外成本。为有效解决此类问题，技术部门决定对加工叶盘的数控机械进刀工艺参数进行优化。

图1 叶盘模型

2 进刀工艺参数优化流程

2.1 刀具尺寸和转角参数最优值的求解

为实现叶盘加工效率和质量的提升，参考已有经验和实际情况，确定最大适用刀具半径和最优转角是解决上述问题最为有效的两个参数。而在这两个参数的优化过程中，又涉及到多个变量，包括叶盘转角以及若干个复杂空间自由曲面上的检查点，使得本文优化求解属于典型的复杂非线性约束优化问题。针对此类问题，选择LSA 线性搜索算法（下文简称为LSA算法）对最大适用刀具半径与最优转角进行求解。

基于已有理论，确定LSA 算法的运行流程如下：①输入转角搜索的初始左、右边界BL、BR，同时输入机床旋转轴的定位精度BP；②计算初始左右边界的适用刀具半径，其存在最大值和最小值，分别用rmax（BL）、rmin（BL）、rmax（BR）、rmin（BR）表示；③取初始左、右边界BL、BR的中点，将其标记为BM，计算该中点的适用刀具半径的最大值、最小值，分别用rmax（BM）、rmin（BM）表示；④计算初始左、右边界BL、BR的差值，如计算结果小于Bp，则以BM为最优转角，并取rmax（BM）和rmin（BM）的最小值作为最大适用刀具的半径值，即rmax=min（rmax（BM），rmin（BM）），而后输出最优转角和rmax，算法结束，否则转入步骤⑤；⑤对沿叶盘轴线正向的被加工曲面和约束曲面的位置关系进行判断，如果被加工曲面在约束曲面的顺时针方向则转移到步骤⑥，逆时针方向则转移至步骤⑦；⑥如果rmax（BM）＞rmin（BM）则令BR=BM，反之则令BL=BM，同时转到步骤②；⑦如rmax（BM）＞rmin（BM）则令BL=BM，反之则令BR=BM，同时转到步骤②。

该算法的基本流程如图2 所示。

图2 LSA 算法基本流程

2.2 刀具选择及加工区域划分

根据实际情况可知，在优化最大适用刀具和最优转角的过程中，刀具的锥度、圆角半径、颈长等参数均为固定值，如果上述参数发生改变，则会导致最大适用刀具在形式和规格两方面发生改变。而在本文叶盘加工过程中，涉及到的刀具种类较多，不能以统一输入参数计算所有切触点的最大适用刀具半径后，再直接进行区域划分。根据上文所述的算法步骤，预先确定加工刀具所处的尺寸范围，按照由大到小的顺序共计选择K 把刀具，这些刀具的直径、锥度、圆角半径、颈长各不相同，因此得到4 个参数对应的4 个集合分别标记为Dr（k）、φ（k）、rc（k）、H（k），然后基于以下步骤对加工过程中单个接触点所需使用的刀具进行分析与确定。

分析工作的关键是对目标接触点对应的最大适用刀具直径Dmax（l）进行分析计算，该步骤以φ（1）、rc（1）、H（1）作为输入参数，并基于上文中所述的算法流程计算：

式中 Dmax——最大适用刀具直径，mm

rmax——刀具半径的最大值，mm

rc——刀具的圆角半径，mm

φ——转角，°

将计算结果与刀具集合Dr（1）中的对应值进行比较，如计算结果高于对应值则该接触点使用1 号刀具进行加工，否则重复上述步骤，令k=k+1 重复进行，直至k=K-1 为止，确定加工刀具的序号。对压力面和吸力面上所有接触点，均采用该方法确定各点加工所需使用的刀具。

在以上分析步骤完成后，结合本文研究的叶盘模型进行加工区域的划分。根据该叶盘模型允许粗加工余量不超过0.5 mm 的要求，确定使用6 把刀具进行加工。6 把刀具的圆角半径均为1 mm，而直径则存在梯度，分别为32 mm、25 mm、20 mm、16 mm、12 mm和8 mm。在对刀具接触点进行判断后，对压力面和吸力面的加工区域进行划分（图3）。

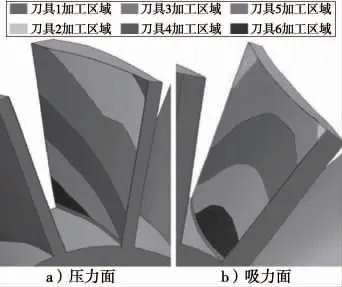
图3 划分结果

2.3 刀位轨迹规划及生成

根据上文对压力面和吸力面的划分，以及最优转角和加工刀具尺寸的分析结果，基于数控机床中的加工坐标系，对刀具的位点坐标（其与切触点一一对应）进行分析，计算公式如下：

式中，PCC（S（i，j））表示在加工坐标系下，接触点为［xCC，yCC，zCC］T时的坐标；n=［nx，ny，nz］T表示加工坐标系CSM 下，曲面在切触点PCC（i，j）处的单位法向矢量。代入已知数据，即可计算得到刀位点信息。该信息以加工坐标系为基础，涵盖了刀位点的空间坐标x、y、z 和刀位点对应的叶盘转角B，格式为［x，y，z，B］。

根据上述计算结果，结合多刀具分区域加工的实际情况，通过以下步骤生成多刀具刀位轨迹：

（1）从尺寸最大的加工刀具开始，按照从叶盘模型尖部向根部的顺序，对所有切削层进行遍历。针对每一个切削层，根据压力面上切削行的类型，生成相对应的刀具加工轨迹，同理可以生成吸力面的刀具加工轨迹。

（2）在此基础上，更换尺寸稍小的下一个加工刀具，按照上述方法生成所需的全部6 个刀具的加工轨迹。

以3 号刀具为例，对刀具加工轨迹的实例进行分析：该刀具从安全平面上的起始点开始，下降至进刀起点，从通道外侧按照进给速度进入到压力面切削段中，实现对压力面的切削。在压力面切削完成后，退回到安全平面。再在安全平面上移动到吸力面切削段的起始点，下降至进刀起点后，进给到吸力面切削的首个点位，再执行对吸力面的切削过程，直至吸力面全部加工完成后执行抬刀动作，使刀具转移至安全平面上的终止点，支持，切削层的加工即全部完成。具体的刀位轨迹如图4 所示。

图4 刀位轨迹

3 实验验证与分析

3.1 实验方案

为验证本文加工进刀工艺方案的有效性，以案例中的叶盘加工为研究对象，分析进刀工艺参数是否能够进行有效加工。因此采用直径为190 mm、厚度为36 mm的硬质铝合金材料作为毛坯进行加工，其控制目标是叶盘轮毂直径为88 mm、轴向厚度为35 mm、叶片高度为46 mm。

确定以上内容后，首先进行实验准备，设置圆角半径rc为1 mm、锥度角度为0°、锥度段长度为35 mm。应用LSA 算法进行优化。结果显示，压力面上最大适用刀具半径的最小值和最大值分别为4.51 mm 和18.27 mm，吸力面上最大适用刀具半径的最小值和最大值则分别为4.28 mm 和14.69 mm。在此基础上，为确保最大尺寸刀具的应用比例尽可能高，在CGTECH软件中进行仿真，对加工区域进行划分，并生成加工刀具轨迹。

在以上工作准备就绪后，采用立式四轴铣床作为主要实验设备，为该机床配置本文所使用的6 种不同尺寸刀具，然后使用计算机对该实验设备进行控制，并执行加工过程。

3.2 实验结果与讨论

（1）对整体实验结果进行评估。根据对实验过程的全程监控可知，在全过程内，刀具和机床、夹具和毛坯材料之间均未发生碰撞，叶盘通道与刀具之间可能的干涉情况也未出现。加工完成后，叶盘的形貌与预期结果基本一致，本文所使用的刀具与加工完成后的效果如图5 所示。

图5 刀具及加工效果

（2）分析加工过程中，各个刀具的加工时间及材料去除比例。本环节通过积分计算方式获取数据信息，结果如表1 所示。

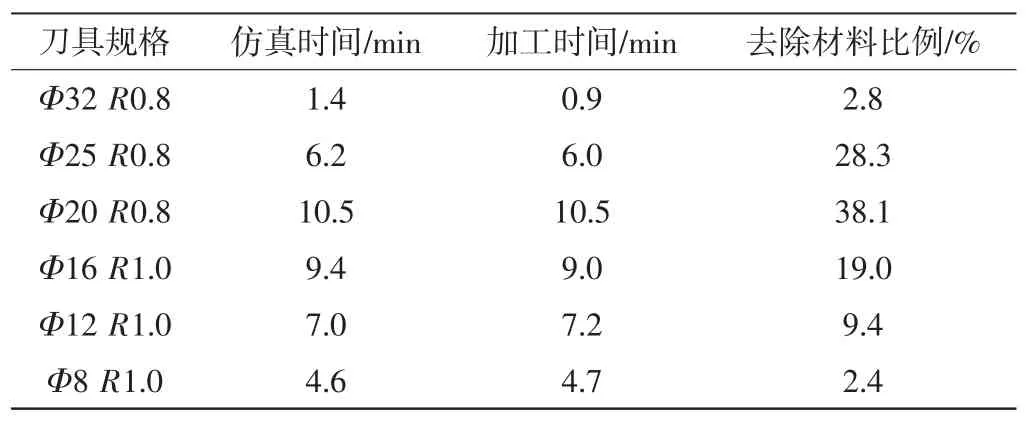
表1 各刀具的加工时间及材料去除比例

由表1 可知，本文加工过程中前3 把刀具贡献了69.2%的切削率，该指标在前4 把刀具中的比例进一步上升，高达88.0%，其他2 把切削尺寸较小的刀具的工作则相对较少。这表明本文研究的最大刀具在叶盘加工方面具有相对较优的性能。

（3）对切削效率的提升情况进行对比分析。与传统模式下仅采用单种刀具的加工模式进行对比，分析结果显示，本文模式与传统模式均取得了100%的去除材料比例，但加工时间差异明显。优化后的模式消耗17.8 min完成了加工，而在传统模式下的消耗为26.2 min，效率提升约32%，表明本文针对进刀工艺的优化取得了一定的效果。

4 结束语

本文针对叶盘器件的数控机械加工展开研究，通过LSA 求解算法对进刀工艺中所需的最大适用刀具半径和最优转角进行了分析计算，并基于求解结果选择加工刀具，对加工轨迹进行规划设计。实验证明，优化后的进刀工艺行之有效，具有一定实际应用价值。