基于多传感器融合的双轮差速机器人定位研究

钱瑞，冯成涛

（常州大学 微电子与控制工程学院，江苏常州，213159）

0 引言

定位是无人驾驶的关键技术之一。现阶段的定位系统主要通过RTK、GPS、IMU、轮式里程计、摄像头、激光雷达等传感器来实现。考虑到单一传感器难以应用于不同复杂多变的环境，多传感器融合的思想应运而生[1]。Thomas 等人[2]在他们的机器人实验平台上搭载了GPS、IMU、轮式里程计这三种传感器，并测试并对比了搭载单一种类传感器与多传感器两种情况得到的定位信息。结果表明，多传感器结合的方案可以显著改善机器人返回位置信息的准确度。

Kalman 于20 世纪60 年代提出的EKF 算法可以对非线性系统进行最优化估计[3]，现已是传感器融合算法的最优选择之一，也广泛应用于定位领域[4]，其可以对特定传感器的数据进行矫正，也可以进行多传感器数据融合，导出最优位置信息。Chen 等人[5]研究了基于GPS、磁力计与INS的连续定位方案，在室外部分采用GPS 定位，室内采用INS 与磁力计获取位置信息，采用卡尔曼滤波解决噪声问题，发现在滤波之后，轨迹噪声下降了2/3。Li 等人[6]研究了基于EKF 的实时VIO 算法，并利用该技术对视觉惯性里程计进行矫正，实验表明这种估计算法具有优良的准确性与一致性。Cai[7]等设计了基于WiFi 与手机惯性导航的室内定位系统，结合两种传感器的适用场景，并基于EKF 算法对其数据进行融合处理，最终实现了高精度的定位系统。

本研究以双轮差速机器人为平台的EKF 数据融合算法，结合基于轮式里程计与IMU 的DR 算法，以及GPS 模块获取机器人位置信息。同时针对DR 积分误差随时间增长的问题，我们将采用GPS 数据直接对DR 进行校准。

1 传感器的选型及其原理

1.1 轮式里程计推算双轮差速机器人航位

本研究采用13 线霍尔编码器来构成轮式里程计，其旋转一圈产生的脉冲数PPR 为390。当电机转动带动编码器的码盘旋转时，根据码盘的编码原理输出A、B 两相正交脉冲信号。微型处理器会根据这两相信号的相位差对编码器计数。

在得到编码器计数值之后，我们可以推出机器人左、右轮速，随后通过建立其运动学模型的方法来实现轮式里程计的功能。在二维理想环境中对机器人进行运动学分析，如图1 和图2 所示。

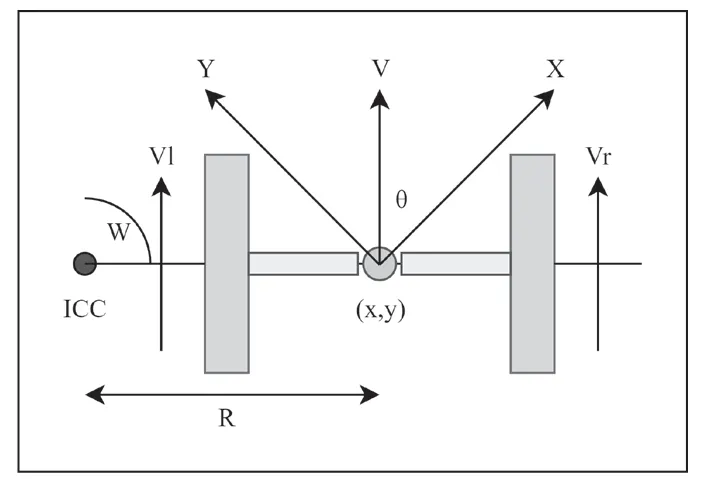
图1 双轮差速机器人运动学建模

图2 双轮差速机器人行驶时的运动模型

上述两图中，（x,y,θ）表示双轮差速机器人在笛卡尔坐标系下某一时刻的位置与姿态信息，（x′,y′,θ′）为经过δt时间（实验中为100ms）后的位置、姿态信息。v和ω分别为其线速度与角速度。假设左轮编码器在某一时刻产生的累计计数值为cnt_1，经过时间间隔δt后累计计数值变为cnt_2，于是可以得到期间机器人的左轮轮速lV：

同理可以求解得到右轮轮速Vr。则双轮差速机器人的运动学方程如公式（3）所示：

其中d为前后时刻两坐标间距，D为机器人车轮半径，实验中D测得为0.065m。

虽然轮式里程计结构简单，易于实现，在理想的环境下可以得到精确位置信息。但是在实际行驶的过程中，编码器难免受到机器人惯性作用以及车轮打滑等因素的影响[8]，使得微机采集到的编码器计数值出现误差，从而导致小车轮速出现误差项vd，并以加性噪声的形式存在于推算出的坐标中，进而在里程计系统长时间的迭代过程中形成不可忽略的积分误差，极大地影响定位的准确度。

1.2 IMU 姿态解算算法

IMU 是用于检测与测量搭载平台加速度与旋转运动的传感器，能够提供平台的姿态角数据。由于采用欧拉角表示描述姿态矩阵时使用大量的三角函数会造成运算量较大的问题，使用四元数法进行姿态角的变换[9]。通常使用数字运动处理器（Digital Motion Processor, DMP）直接读取四元数，或者用互补滤波、扩展卡尔曼滤波等数据融合算法对加速度计与陀螺仪的测量结果进行融合[10,11]。

我们选用MPU6050 模块检测机器人的姿态信息，其内部包含三轴陀螺仪与三轴加速度计，由自带的DMP 对六轴数据进行整合[9]。

用I2C 总线与MPU6050 通信，读取三轴加速度计与三轴陀螺仪测量到的加速度与角速度值，计算出表示姿态角的四元数据q0、1q、q2、q3[10]，通过下述公式（4）可以解算出机器人的横滚角（Roll）、航偏角（Yaw）和俯仰角（Pitch），分别用Φ、Ψ 和θ表示，并分别对应指向东天北坐标系（ENU）中的东、北和天向[12]：

由此便可以获得机器人行驶过程中的姿态信息。本研究主要使用IMU 来以取平台航偏角Ψ 信息，以替代轮式里程计推算模型中的航向角θ。

但是MPU6050 等低成本IMU 会受到扰动噪声、随机漂移、零偏等干扰因素的影响[13]，随着时间累积，这些干扰项对的传感器输出结果的影响会越来越大，最终导致其无法为机器人提供准确的姿态信息。

1.3 GPS 定位

GPS 定位具有高精度、测量时间短、可全天候作业的优势[13]，可以为搭载平台提供稳定可靠的定位服务以及获取姿态信息。本研究采用由U-BOX 公司设计的NEO-6M GPS 模块来确定双轮差速机器人的位置信息。实验中我们采用RS232 串口与其进行通信，通过读取到的GPRMC 最小定位语句，我们可以确定某一时刻机器人的经、纬坐标、地面速率、地面航向以及UTC 日期等信息。经过坐标转换，我们将WGS-84 坐标系下的位置信息转换到ENU 坐标系中，得到四个状态参数：横坐标x、纵坐标y、航向角θ以及线速度v，方便其与IMU 以及轮式里程计数据融合。但是，在隧道与高楼环境中，GPS 信号将受到不可忽视的噪声干扰，产生多径效应，其定位结果将不再可信，所以单一GPS 模块的应用受限于使用场景[14]。

1.4 融合算法

由上文分析可得，轮式里程计与IMU 组成的DR 系统抗干扰的能力较强，泛用性强。但是在长期独立工作的情况下，DR 由于模型误差、传感器精度以及漂移等问题，导致其积分误差随着时间的增长而急速增加，从而无法再发挥功能。

而GPS 几乎不会为积分误差所困扰。它可以为机器人提供全天候的实时绝对定位信息。然而在遇到卫星信号为建筑物所遮挡的情况的时候，GPS 传回的位置信息就会受到极大的干扰，可信度不再。

所以，在DR 与GPS 相结合的定位系统中，我们使用DR 对机器人的航位进行推算，同时使用频率较低的GPS 对DR 对推算进行修正，取长补短。

2 模型与方法

2.1 基于扩展卡尔曼滤波的模型最优估计推导

卡尔曼滤波器（KF）利用上一刻系统状态的最优解来预测当前系统状态的值，同时使用观测值来修正当前值，以得到最优解。

扩展卡尔曼滤波器（EKF）是对一般卡尔曼滤波器在非线性状态下的扩展，与一般的卡尔曼滤波器一样，也分为预测和两大步骤。

2.1.1 模型的状态方程

我们取双轮差速机器人在笛卡尔坐标系下的横坐标x、纵坐标y、航向角θ、线速度v以及角速度ω这5 个维度的状态数值作为其的状态向量：

其中v与ω由轮式里程计和IMU 直接测量得到，其余三个状态量将由前文建立的双轮差速机器人运动学模型推算得出。对上述的状态向量进行简易运动学分析（如图3所示），得到如下状态方程：

图3 双轮差速机器人行驶时的简易运动模型

f（xt-1）是系统的非线性状态转移函数，考虑到模型的误差，我们可以将系统的状态方程进一步优化成如下方程：

其中，ωt-1是模型的过程噪声，假设其服从数学期望为0，方差为Q 的正态分布。

2.1.2 模型的观测方程

取机器人在笛卡尔坐标系下的横坐标x、纵坐标y、航向角θ以及线速度ν这4 个维度的状态数值作为观测方程Ζt。可以用如下方程描述GPS 对其的状态的观测：

其中，vt-1是模型的观测噪声，假设其服从数学期望为0，方差为R的正态分布；h为将状态映射到测量空间的非线性传感器模型。

2.1.3 EKF 的预测步

通过前面得到的状态方程与观测方程我们可以写出系统的先验故估计方程及其协方差矩阵：

其中F 为状态转移矩阵。由于该模型中，机器人的航向角θ、横坐标x、纵坐标y均由线速度与角速度推导得出，所以模型误差来源于线加速度av以及角加速度aω，设其误差值分别为vaδ与aωδ，可以推导得出过程噪声的方差Q：

其中vaδ与aωδ需要手动调定，当给定值越大，说明对齐信任度越低，而给定值越小，说明对其信任度越高。

2.1.4 EKF 的更新步

其中H 为测量矩阵。卡尔曼增益K是卡尔曼滤波器更新步中最为核心的变量。我们希望最优估计值能够尽量逼近真实值xt，从式（13）中可以看出，这一定程度上取决于观测值与预测值在模型中的权重。K 值较大，说明我们更加信任观测值；反之则说明我们更加信任预测值。通过调整Q、R 两个矩阵的初值，可以决定K 值大小。实验过程中GPS 模块传回的观测值是我们更倾向于信任的，所以赋予观测噪声R 的初值较小，而过程噪声Q 的初值较大，得到K 值较大。

2.1.5 EKF 的状态转移矩阵

由于线性噪声wt1-、vt在通过非线性系统之后，会变成非线性的信号。在EKF 中，我们习惯于对非线性量采用泰勒级数展开，将非线性公式为线性公式，然后对每个单独状态变量分别求偏导，得到一个5*5 的雅可比矩。上述公式中提及的状态转移矩阵F 和H 分别为状态方程xt和观测方程zt的雅可比矩阵：

2.2 使用互补滤波解算MPU6050 姿态角

2.2.1 互补滤波

由于加速度计具有较好的静态特性，而陀螺仪在高频段动态响应特性好。所以对加速度计采用低通滤波、对陀螺仪采用高通滤波，通过互补算法就可以得到高频和低频动态响应特性都很好的数据[10]。

对陀螺仪输出的角速度积分，可以得到我们所需要的角度，但是由于陀螺仪存在误差，且这个误差会随着时间的变化累加。在互补滤波中，我们采用加速度计对误差进行补偿。首先规定误差的定义：

我们在机体坐标系中对陀螺仪的误差进行纠正。当由地理坐标系旋转得到机体坐标系时，需要用四元数表示坐标系的转换，即如公式（18）所示的旋转矩阵[15]：

由于当加速度计处于静止状态时，输出恒为[ 0 0g]，其中g表示重力加速度。则可以得到机体坐标系重力向量：

用加速度计纠正陀螺仪，可以用PI 算法对角速度进行误差补偿，其中补偿量如下：

其中Kp为比例系数，Ki为积分系数。调节Kp与Ki的值将直接影响互补滤波的效果：Kp越大，则越信任加速度计的测量值；Kp越小则越信任陀螺仪的测量值。将补偿量累加可以得到修正后陀螺仪数据：

其中T表示控制周期。将计算得到的四元数代入公式（4）便能解出欧拉角所描述的姿态矩阵。

2.2.2 互补滤波调参

由于互补滤波算法控制系统的特征多项式为如下形式[16]：

我们分别用时间常数τ与无阻尼振荡频率nω表示Kp与Ki：

通常认为阻尼比ξ的值为0.707 时系统的稳态响应最好，于是我们可以得到Kp：

于是调节nω的值便可实现对Kp与Ki的调参，从而改变互补滤波的结果。

经过调试，我们取ωn= 0.31。

2.3 航位推算算法的改进

考虑到本研究构建的轮式里程计模型与IMU 测量数据会随着时间累计产生积分误差，以至于超出阈值，进而干扰定位结果。我们计划首先在一开始使用GPS 数据第一帧对DR 初始化，矫正其航向与位置，并消除IMU 的零点漂移。同时每间隔一段时间 1tδ（实验中为10s），我们用GPS 传回的位置及姿态信息对DR 推算模型的航向角以及x、y坐标进行修正，即用相同时间戳对应的数据替代上述待修正值，防止DR 模型产生过大的积分误差。在接下来实验与仿真部分，我们将比对DR 修正前后机器人的定位轨迹，以说明该算法的优越性。本研究具体的算法流程如图4 所示。

图4 传感器融合流程框图

3 实验与仿真

3.1 实验与仿真

我们的实验平台是一个双轮差速机器人。其装备了霍尔编码器，来实现轮式里程计的功能。通过编码器传回的数据得到左、右轮速，对机器人的运动学模型进行分析，便可以推算出其线速度、角速度以及平面坐标。此外，平台装备了一个MPU6050 模块与一个NEO-6M 模块。IMU 传感器来读取Yaw 角数据作为机器人航向角的观测值，GPS 模块实时传回观测的其线速度、航向角与经纬坐标。

在选择姿态角解算方法的时候，我们比对了互补滤波与DMP 姿态解算的效果：将IMU 模块分别绕着纵笛卡尔坐标系的X、Y、Z 轴旋转90°，得到相应的Roll、Pitch 和Yaw角数据，随后对采集到的数据进行处理，分别得到图6、7、8 所示的结果，经过比对，选择解算效果更好的方法到数据融合中。

图6 DMP 四元数解算（蓝色曲线）与互补滤波姿态解算YAW 角效果

图7 DMP 四元数解算（蓝色曲线）与互补滤波姿态解算PITCH 角效果

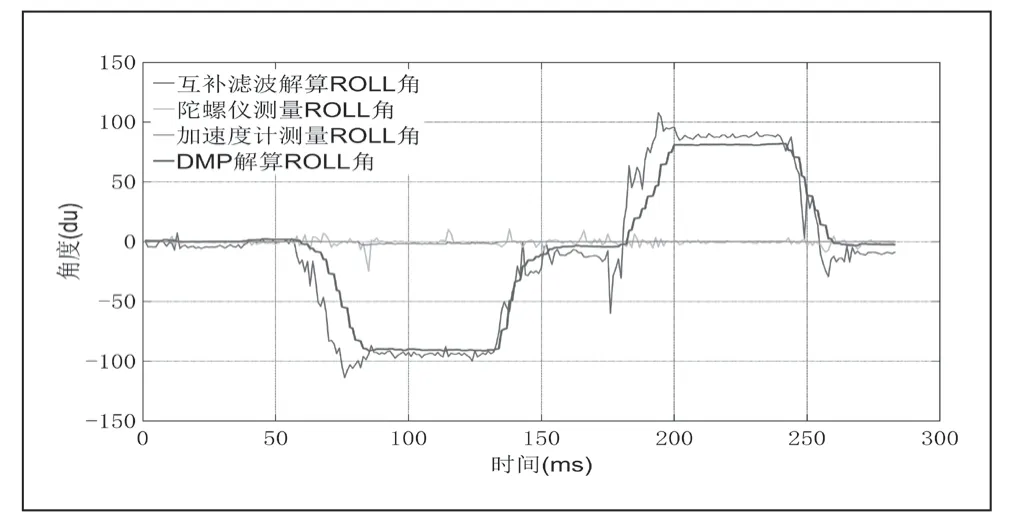
图8 DMP 四元数解算（蓝色曲线）与互补滤波姿态解算ROLL 角效果

由于GPS 模块得到的位置信息基于经纬高坐标系（LLA），无法直接与轮式里程计推算的位置信息直接进行数据融合，所以我们需要将位置信息转换到转换为东北天坐标系（ENU）下，具体步骤是先将LLA 下的数据转换到地心地固直角坐标系（ECEF）下，再将ECEF 中的位置信息转换到ENU 中。

坐标转换结束之后，便可以通过前面提及的方法对三个传感器的数据进行融合。值得注意的是，轮式里程计与IMU的采样频率均为10Hz，而GPS 模块的采样频率为1Hz。所以以GPS 数据为基准，对IMU 与轮式里程计返回的数据进行同步，其中对IMU 的预处理不仅仅是降采样，还包括了对两个采样点之间的数据进行的均值滤波。最后，将预处理完成的数据代入EKF 数学模型中，对小车的实际位置信息进行最优估计。

3.2 实验结果分析

对比图6、7、8 中互补滤波的效果，发现对Roll 角和Pitch 进行互补滤波的效果较好，但是对YAW 角进行互补滤波效果很差。同时，互补滤波容易受高频噪声影响，当IMU 从相对静止的状态开始翻转时，往往互补滤波的结果会出现较大的突变，这对于DR 推算的结果会产生不利的影响；相较之下，DMP 四元数解算得到的姿态角几乎不受噪声影响，效果很好。

之后，我们对互补滤波输出结果进行低通滤波，试图滤除干扰以得到更加可靠的结果，如图9 所示。

图9 IMU 的Roll 角旋转时互补滤波结果、加入低通滤波器后互补滤波的结果与DMP 四元数解算结果（黑色曲线）比较

可以发现，尽管低通滤波器滤除了许多高频噪声，但是滤波后的结果对比滤波前的结果滞后了8 个采样点，即800毫秒，且整体波形的平滑度仍不及DMP 四元数解算结果。所以在进行数据融合的时候，我们选用实验中表现更好的DMP 解算机器人的Yaw 角数据，用于最终的数据融合中。

我们将采集结束的数据在matlab 中进行时间戳对齐之后，直接代入EKF 模型，我们可以得到机器人位置的最优估计，并将DR 推算、GPS 观测与融合结果三条曲线整合到同一张图中（图10、图11）以便与真实路径进行直观的比对。

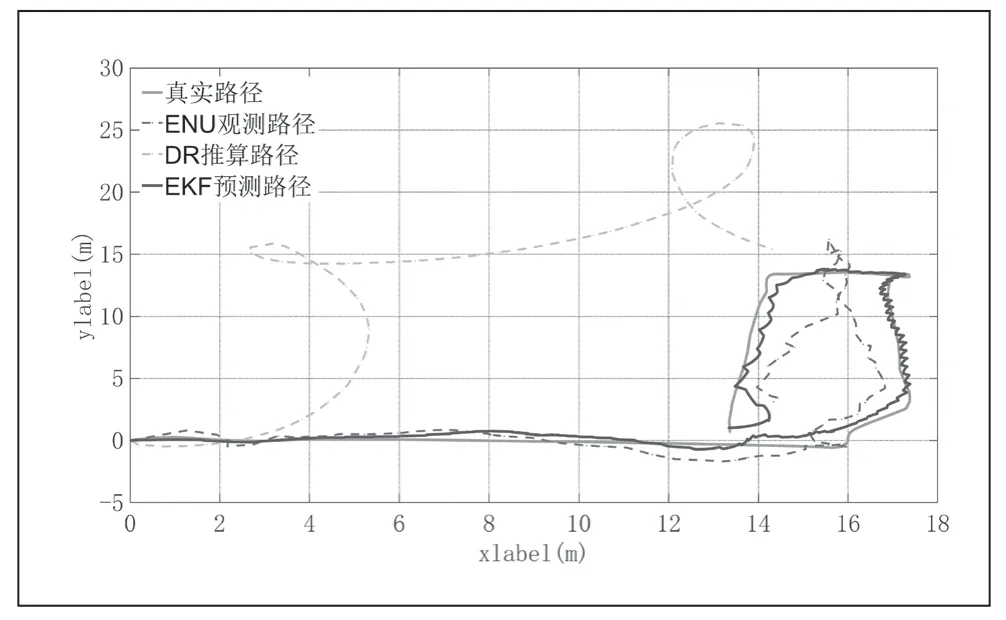
图10 DR 推算、GPS 观测、EKF 融合结果三种轨迹与真实轨迹对比。其中红色曲线为EKF 预测结果（我们数据融合得到的结果）、黄色曲线为DR 推断结果、蓝色曲线为GPS 观测结果、绿色曲线为真实路径

图11 DR 推算、GPS 观测结果与真实路径的比较（图片上半部分）。EKF 融合结果与真实路径的比较（图片下半部分）。

观察图10 与图11 中的比较结果，可以发现DR 推算结果是最差的，其终点与真实路径终点相差为14.79 米；GPS单独观测的结果与真实路径终点相差1.29 米；而EKF 融合结果毋庸置疑是最好的，与实际终点相差仅有0.5814 米。

直接对比图中路径可以发现DR 推算结果与真实路径相差甚远，而虽然GPS 直接观测得到的路径相较DR 要更加贴合真实路径，在机器人第二次转弯附近，其观测结果还是出现了较大误差。最后，用红色曲线表示的EKF 融合得到的路径很明显是最佳的，与真实路径的贴合程度最高。

因此，采用扩展卡尔曼滤波可以有效地提升传感器对机器人的定位精度。

4 结束语

本文介绍了基于卡尔曼滤波的多传感器数据信息融合，将DR 推算的结果与GPS 观测的结果相结合，解算双轮差速机器人的航位信息。我们比较了纯DR 推算与GPS+DR两种方案与预定轨迹的偏差，发现多传感器融合的定位系统可以极大地改善定位结果的准确性。

同时，在IMU 姿态解算方式的性能上，我们也发现DMP 硬件解算的方法是优于互补滤波算法所得结果的。

在实际应用中一般会借助路网信息、高精地图等其他无人驾驶关键技术来辅助机器人定位。那么如何学习并使用上述方法为机器人定位以及更好地解决此类问题也无疑会成为我们接下来研究的方向。