船舶用AH32钢常温抗拉强度测量结果不确定度评定

陆雷俊, 黄帅金, 吉宏林, 孙宝民, 代雪佳

(上海船舶工艺研究所, 上海 200032)

金属材料拉伸试验广泛应用在国防、能源、船舶、航空、航天、兵器等领域,拉伸试验主要用于测试金属材料的抗拉强度、屈服强度、断面收缩率等力学性能。不同牌号、不同批次、相同金属材料的强度和韧性等具有可比性,能直接用于材料研发、质量控制、国内外贸易、工业标准互认等相关工业活动。

在金属材料拉伸试验方法中,常温拉伸试验方法使用频率较高,金属材料的常温拉伸试验方法受设备、工艺、技术等因素的影响,得到的数据具有相对离散性。为全面评价试验数据并对材料性能做出适当评估,有必要对试验数据进行不确定度分析。

在建造船舶时,由于工作人员大量使用金属材料,故需要对船舶用钢进行理化检验,其中拉伸试验是不可缺少的重要试验项目,其测量结果的不确定度评价在材料研发、验收等过程中也尤为重要。

1 拉伸试验方法及不确定度来源

GB/T 228.1—2021 《金属材料 拉伸试验 第1部分:室温试验方法》中的拉伸速率控制方法A在实验室具体操作时较难实现[1],方法A的控制模式对设备应变控制器及试验人员的素质要求较高,普通试验机较难实现该方法;方法B是目前实验室普遍使用的可靠速率控制方法。该拉伸试验方法采用方法B的试验速率控制模式,计算机控制试验过程,自动采集试验数据,自动生成试验曲线。

在确定抗拉强度测量结果不确定度时,在考虑数学模型及试验条件存在不完善可能性的同时,还需要考虑试样具有分散性,即每个试样真值在客观上是具有差别的,试样本身具有一定的不确定度[2-3]。经综合考量,船舶用钢常温拉伸试验不确定度来源确定及评定方法如表1所示,试验时π取3.141 6。

表1 船舶用钢常温拉伸试验不确定度来源确定及评定方法

2 数学模型

2.1 抗拉强度计算数学模型

根据拉伸试验抗拉强度Rm计算的数学模型如式(1)所示。

(1)

式中:d为拉伸试样直径;A为拉伸试样截面积;Fm为最大拉力。

2.2 抗拉强度不确定度数学模型

拉伸试验抗拉强度不确定度数学模型如式(2)所示。

ucrel(Rm)=

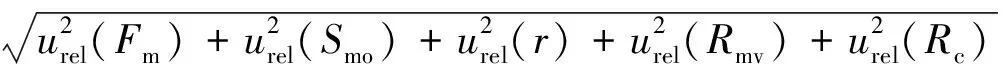
(2)

3 试验仪器

试验仪器为WDW-300KN型电子材料试验机,计量精度为1级;外径千分尺量程为0～25 mm,计量精度为0.01 mm。标准测力仪等级为0.3级;拉伸试样材料为AH32钢,为圆形棒状,试样相关尺寸符合GB/T 228.1—2021对标准试样的要求,直径为10 mm。

环境要求:试验一般在10～35 ℃的室温环境中进行,将实验室温度控制为(23±3) ℃,湿度控制为不大于70%。

4 拉伸试验不确定度评定及分析

4.1 试样重复性引入的不确定度评定

按照GB/T 228.1—2021标准推荐,用拉伸试验机测试10个同炉批试样,在相同条件下,可认为是重复测定同一试样,所得抗拉强度分别为435,433,429,427,430,429,435,438,436,431 MPa,均值为432.300 MPa,相对标准偏差为0.795%。

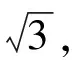
4.2 拉力引入的不确定度urel(Fm)评定及分析

4.2.1 测力系统示值误差引入的不确定度

4.2.2 标准测力仪校准误差引入的不确定度

检定试验机及标准测力仪最大允许误差为0.3级,该校准源的不确定度为0.3%,包含因子为2[5],由此引入的B类评定相对标准不确定度urel(Fm2)=0.15%。

4.2.3 计算机采集系统引入的不确定度

计算机数据采集系统引入的B类相对不确定度urel(Fm3)不大于0.35%。

4.2.4 拉力引入的不确定度合成

拉力引入的不确定度合成urel(Fm)=0.691%。

4.2.5 拉力引入的不确定度分析

拉力相对不确定度urel(Fm)的评定影响因素较多,引入示值误差、测力仪误差(最大误差)及计算机采集系统带来的误差,能基本反映拉力不确定度的分布情况,分析得到的拉力不确定度具有可操作性和针对性。

4.3 试棒直径测量不确定度

4.3.1 试样原始直径d0测量截面变化引起的相对不确定度分量

表2 圆棒试样直径测量结果 mm

4.3.1.1 合并样本标准差

根据CNAS-GL009:2018 《材料理化检验不确定度评估指南及实例》,试样直径测量重复性引入的不确定度分量采用高可靠性的合并样本标准差,即每次核查的自由度相等(每次核查时测量次数相同)。

根据表2数据,试样测量直径合并样本标准偏差Sp为0.043 71 mm。

4.3.1.2 样本标准差数列合并标准差

4.3.1.3 标准差数列估算标准差

直径测量重复性不确定度标准差数列估算标准差如式(3)所示。

(3)

4.3.1.4 试棒直径测量不确定度取值

4.3.1.5 试样直径测量不确定度分析

试样直径测量不确定度受测量加工精度、人员、截面等因素影响,直径测量不确定度一般占抗拉强度不确定度的权重较大,提高加工精度可以有效降低抗拉强度不确定度,从而提供更加可靠的试验数据。

4.3.2 千分尺精度引入的不确定度分量

经计量,合格极限示值误差为0.01 mm,即误差范围为±0.01 mm,并且在该区间服从均匀分布,由此引入的B类评定相对不确定度urel(Smo2)=u2(d0)=0.005 8 mm。

4.3.3 试样原始直径测量引入的不确定度分量合成

因为d0所得不确定度是测量重复性引起的,和示值误差不确定度相互独立,试样原始直径引入的合成相对不确定度urel(Smo) 为0.884%。

4.3.4 试样直径测量不确定度分析

试样直径测量不确定度评价时,考虑采用不同径向、人员开展重复性测量,并引入测量尺精度(最大精度误差),这样分析得到的直径测量相对不确定度更符合实际测量情况,能基本反映直径测量不确定度。

4.4 拉伸速率引入的不确定度

4.4.1 拉伸速率引入不确定度分量计算

拉伸速率不确定度是评价横梁位移速率造成的不确定度,其数值受横梁刚性、第一速和第二速变换等因素影响,拉伸曲线容易出现跳跃,拉伸速率明显影响到抗拉强度的测试结果。

拉伸试验机横梁速率校准不确定度为0.3%(k=2.0),由拉伸速率引入的相对不确定度拉伸速率不确定度urel(Rmv)为0.173 4%。

4.4.2 拉伸速率引入不确定度分析

抗拉强度Rm随着拉伸速率的增大而增大[6],在某些高可靠性、高精度要求条件下,可以开展不同拉伸速率条件下的测试,找到相关趋势,分析拉伸速率对抗拉强度的影响。为规范拉伸速率的影响,采用机器定期校准报告中工作速率下的横梁速率校准不确定度作为拉伸速率不确定度引入值,具有一定代表性和可操作性。

4.5 修约不确定度

按照GB/T 228.1—2021规定,将抗拉强度修约至1 MPa,分布区间半宽为0.5 MPa,由修约引入的相对标准不确定度Urel(Rc)为0.067%。

4.6 抗拉强度不确定度汇总及合成

4.6.1 抗拉强度不确定度汇总

首先,在众多抗拉强度不确定度影响分量中,圆棒试样直径不确定度的影响最大,说明提高其直径加工精度能明显改变抗拉强度不确定度;其次,采用测试组内极差作为拉伸速率不确定度分析依据,得到的不确定度影响仅次于圆棒试样直径不确定度,作为拉伸速率不确定度引入有一定可操作性;拉力不确定度取决于设备、附件等系统精度。按实例结果分析可知,在其他不确定度分量相对稳定的情况下,提升圆棒试样直径加工精度可以改善抗拉强度不确定度。

抗拉强度相对不确定度分量具体汇总如表3所示。

表3 抗拉强度相对不确定度分量汇总

4.6.2 抗拉强度相对不确定度合成

抗拉强度相对不确定度合成如式(4)所示。

ucrel(Rm)=

(4)

得到ucrel(Rm)为1.236 0%。

4.6.3 抗拉强度相对扩展不确定度

取概率为95%,置信因子k=2.0,则抗拉强度相对扩展不确定度uKrel(Rm)为2.472 0%。

抗拉强度扩展不确定度为10.68 MPa,取10.7 MPa。

4.7 抗拉强度不确定度报告

置信概率为95%(k=2.0)条件下,该试验扩展相对不确定度为2.472 0%,拉伸示值相对扩展不确定度为(432±10.7) MPa。

5 结论

(1) 该批次船舶用钢(AH32)常温抗拉强度在置信概率为95%(k=2.0)条件下,相对不确定度为2.472 0%,扩展不确定度为(432±10.7) MPa。

(2) 为规范拉伸速率的影响,采用机器定期校准报告中工作速率下的横梁速率校准不确定度作为拉伸速率不确定度引入值,具有一定代表性和可操作性。

(3) 直径测量不确定度一般占抗拉强度不确定度的权重较大,提高加工精度可以有效降低抗拉强度不确定度,以提供更加可靠的试验数据。