基于希尔伯特-黄变换与小波分析的降雨序列多时间尺度研究
贺军奇,郭鑫佳,陈云飞,刘秀花,高万德,龙婷
(1.长安大学水利与环境学院,西安 710054;2.旱区地下水与生态效应教育部重点实验室,西安 710054;3.水利部旱区生态水文与水安全重点实验室,西安 710054)
降雨是一个复杂的自然过程,受到诸多因素的影响,其序列往往是非线性、非平稳的,并伴随着一定的随机性和周期性[1]。特别是近年来全球气候变暖和人类活动的叠加影响,不仅加快了区域尺度上的水文循环过程,也加剧了降雨的区域差异性和不确定性[2]。针对降雨序列表现出的多时间尺度、多频率的变化特性,水文周期分析方法经历了从时间域到时频域的发展历程[3]。其中,Fourier变换因其时频分析特性自1965年来便得到广泛应用,但受Heisenberg不确定性原理的限制[4],Fourier变换不能刻画任意时刻的频率成分,会在某种尺度上掩盖序列特征[5]。随后以其为基础发展的小波分析被更多地用于研究降雨序列的多尺度变化规律和演变趋势,虽然小波分析使用可调时频窗解决了时间和频率分辨率的矛盾,具有良好的时频局部化特征和多分辨率能力,但其本质上仍是一种窗口可调的Fourier变换,依然存在Fourier变换的局限[6]。
希尔伯特-黄变换(Hilbert-Huang Transform,HHT)是Huang等在1998年提出的一种时频分析方法,主要由经验模态分解(Empirical Mode Decomposition,EMD)和希尔伯特谱分析(Hilbert Transform,HT)两部分组成:通过EMD 对非线性、非平稳信号逐级进行线性化和平稳化处理,在保留数据特性的同时把不同尺度的波动和变异分离出来;随后通过HT 求解瞬时频率进一步强化数据的局部特征,从而精确地给出频率与时间的对应关系,使HHT 不再受不确定性原理的限制[7]。因此该方法在目前的水文序列多尺度研究中得到了较多应用。如周生辉等[8]通过EMD 分析了1959—2019年海流兔河流域周边3个气象站的降雨周期变化特征;Luo 等[9]利用HHT 识别径流与产沙量的多时间尺度特征,并通过描述两个变量在不同尺度上的关联性阐明其内在的产沙机制;邵骏等[10]利用HHT 对雅鲁藏布江干支流上的10个水文站1956—2000年的天然径流量进行分析,探讨了雅鲁藏布江流域年径流变化的近似周期及其演变趋势。此外,为提高周期特征的识别精度,近年来一些研究也尝试将改进后的HHT 引入水文分析中。如范琳琳等[11]将基于T 检验改进的HHT 用于长江宜昌水文站50 a日径流量的分析中,识别出径流在不同时间尺度上的年际变化周期;余世鹏等[12]为了消除HHT 可能存在的模态混叠现象,利用基于集合经验模态分解(Ensemble Empirical Mode Decomposition,EEMD)改进的H HT 剖析了滨海围垦滩涂区域降水的多尺度周期特征,并指出改进的HHT 能获取更准确的周期尺度特征。
然而,目前大多数研究都侧重于HHT 的实例应用,缺少与传统周期识别方法的对比,同时也缺乏分析区域尺度上降雨周期演变特征的可靠方法。因此,本文基于多元经验模态分解(Multivariate Empirical Mode Decomposition,MEMD)获取多变量共同尺度的优势,提出将其应用于区域尺度降雨周期演变特征的提取。在此基础上,采用2组已知成分的人工序列对比分析基于MEMD 改进的HHT(后称HHT)和传统小波分析在周期识别准确性上的差异;随后通过毛乌素沙地11个气象站点的实测降雨序列,进一步探讨HHT 在推求区域降雨序列周期演变特征上的适用性。本研究不仅能为区域水文周期分析方法的选择提供更多参考,同时也通过研究毛乌素沙地降雨周期的演变特征,为旱涝灾害应对和区域水资源管理提供一定的科学依据。
1 方法与数据
1.1 HHT的基本理论及特性
EMD 作为原始HHT 的基本理论,可以将复杂的原始数据分解为若干固有经验模态函数(Intrinsic Mode Function,IMF)和残差项(Residual)的有限组合。在本研究中,采用MEMD 取代原有的EMD 以改进HHT。MEMD 是标准EMD 的多元扩展,通过引入映射概念,将含有多个变量的信号组在不同空间中沿不同方向投影,生成多维包络线[13]。然后计算多元变量的局部平均值,确保多个变量的IMF 分量在振荡频率和数量上的同步性,从而实现不同频率尺度下多变量的共同模式分解[14]。
假设代表降雨的n维矢量数据S(t)={s1(t),s2(t),…,sn(t)}是数据t的函数,Xθk={xk1,xk2,…,xkn}是角度矢量θk={θk1,θk2,…,θkn-1}(k=1,2,…,N)定义的沿着不同方向的矢量数据,其中N是所有方向的个数。
非线性的k个空间数据的MEMD具体步骤如下[15]:
(1)获取合适的n维方向矢量数据集X;
(2)计算时间序列S(t)沿着给定方向Xθk的投影pθk(t);
(3)识别每一个方向向量上pθk(t)极值出现的位置tθki;
(4)通过多元样条插值函数插值〔tθki,S(tθki)〕,获取多元包络曲线eθk(t);
(5)计算包络线均值M(t),公式如下:
(6)通过D(t)=S(t)-M(t)得到IMF。假如D(t)满足多元IMF 的判断标准,则D(t)作为IMF保存,将S(t)=S(t)-D(t)作为步骤(2)的输入变量。如果不满足,则将S(t)=D(t)作为步骤(2)的输入变量,继续进行迭代运算(图1)[16]。

图1 MEMD流程示意图Fig.1 Schematic diagram of MEMD process
HT 作为HHT 的核心内容,其目的是得到能充分反映S(t)时—频—能量分布的瞬时频率,使分解得到的每个IMF 都有着明确的物理意义(即时间尺度周期)[17]。具体计算过程如下:对IMFi(t)进行HT 转换(公式2);提取瞬时频率和振幅(公式3);最终得到能反映信号能量在时间和频率上分布规律的Hilbert谱(公式4):
式中:P.V.表示Cauchy主值积分,ωi(t)和ai(t)分别为瞬时频率和振幅。
1.2 小波分析的基本理论及特性
小波是一种传统的时频多分辨率分析方法,在进行时间序列分析时,通常选用可以较好表达相位信息的复值小波。其中,Morlet小波在时频空间的局部性较好,因此常被用于降雨径流时间序列分析[18]。本研究使用的Morlet小波解析形式为[19]:
式中:i为虚部单位;w0为无量纲频率,t为时间。
对于时间序列f(t)∈L2(R),其连续小波变化为:
在时间域上不同尺度a的所有小波系数Wf(a,b)的平方值对位移因子b进行积分,得到小波方差的计算公式:
为减小序列边界端点效应的影响,利用MATLAB小波工具箱中的信号延伸(Signal Extension)功能,采用对称、周期延伸法对距平后的降雨数据两端进行延展。然后,计算其复小波系数,删除延伸数据的系数后,计算Mrolet复小波系数的实部、模、模方和方差。
1.3 配对样本t检验
配对样本检验是针对配对数据的t检验,可以用来检验两组数据是否有差别。设X1,X2表示两个随机的成对样本,两个变量的n对观测值形成配对样本,它们可以表示为(X11,X21),(X12,X22),…,(X1n,X2n),计算每一对样本观察值之差,记为dj,进一步得到其均值和标准差Sd。假设H0:μ1-μ2=μd=0,H1:μd≠0。此时检验统计量为[20]:
在原假设成立的条件下,它服从自由度为〔n-1〕的t分布。对应的伴随概率小于设定的显著性水平,则拒绝两组样本均值相等的假设。将人工序列的预设周期分别与不同方法的计算结果进行配对样本t检验,以分析不同方法在周期识别方面的准确性。本次研究显著性水平设置为0.05。
1.4 数据资料
使用人工序列和实测降雨序列综合对比HHT和小波分析在多周期尺度分析的准确性和适用性。参考姜瑶等的研究案例[21],创建2组已知成分的人工序列数据测试对比H HT 和小波分析在周期识别方面的准确性,并探讨造成不同方法性能差异的主要原因。第1组数据考虑不同的趋势变化,并在此基础上叠加相同的周期和随机波动;第2组数据无趋势变化,在此基础上叠加不同的周期和随机波动。所有序列的长度均为120 a,详细内容见表1和图2。

表1 人工序列数据的主要信息Table 1 Main information of artificial sequence data

图2 人工序列数据示意图Fig.2 Schematic diagram of manual sequence data
实测序列采用1982—2020年毛乌素沙地11个气象站点的逐日降雨数据计算各站点的逐年降雨量(包含冬季降雪),数据源自中国气象数据网(http:∥data.cma.cn)。获取数据后,统一对所有站点的降雨数据进行质量检查与校正,主要包括:检查降雨数据是否有缺失,对缺失数据进行插补;删除多余的重复数据;对异常值进行修正等。
如图3所示,毛乌素沙地39 a年均降雨量在170~440 mm:沙地西部降雨较少,年平均降雨量为170~200 mm,包含陶乐站(S6),银川站(S7)以及吴忠站(S9);中部次之,年平均降雨量为270~350 mm,包含定边站(S3),盐池站(S8)以及鄂托克旗站(S10);东部降雨较多,年平均降雨量为360~440 mm,包含榆林站(S1),神木站(S2),靖边站(S4),横山站(S5)以及伊金霍洛旗站点(S11)。

图3 1982-2020年年均实测降雨空间分布图Fig.3 Spatial distribution map of annual average measured rainfall from 1982 to 2020
2 结果与分析
2.1 人工序列周期识别结果
图4和图5分别为HHT 对2组人工序列的分解结果。括号内的数字表示各个IMF和残差分量占原始序列的方差相对贡献率,该值表征了IMF 分量对原始序列的影响程度,方差贡献率越大,IMF影响越大,代表性越强。由于数据驱动的自适应性,第1组人工序列(M1,M2及M3)经MEMD 分解后得到了7个IMF和1个残差分量;第2组人工序列(M1,M4及M5)经分解后得到了6个IMF和1个残差分量。从IMF1到残差分量,数据振荡幅度逐渐减小,波长逐渐增大,体现了从高频—低频的转变,反映了各分量所代表的时间尺度的周期变化特征。以M1为例,经HT 变换后得到各模态(IMF1-7)对应的时间表征尺度分别为2.9 a,4.7 a,12.1 a,24.1 a,30.4 a,56.4 a以及119.1 a(表2)。通过对比各序列的所有IMF分量,可以发现IMF3的方差贡献率占据了原始序列的80%以上,这表明两组人工序列的周期以IMF3分量的周期为主,进而得到M1,M2和M3的周期分别为12.1 a,12.2 a和12.2 a;M1,M4和M5的周期分别为12.1 a,14.9 a和10.1 a,与表1的预设周期几乎一致。此外,图中的残差分量均能很好地展示图2原始数据的趋势变化,这表明MEMD 能很好地提取2组数据的局部特征和趋势变化。总的来说,H HT 不仅能准确识别5个变量各个尺度下的周期特征,还具备很好的趋势检测性能。

表2 基于人工序列使用HHT得到的各固有模态函数周期表Table 2 The periodic table of each intrinsic mode function obtained by HHT based on the artificial generated sequence a

图4 基于第1组人工序列M1,M2,M3使用HHT分解得到的固有模态函数(IMF1-7)和残差项Fig.4 The intrinsic mode function(IMF1-7)and residual term decomposed by HHT based on the first set of artificially generated sequences M1,M2 and M3
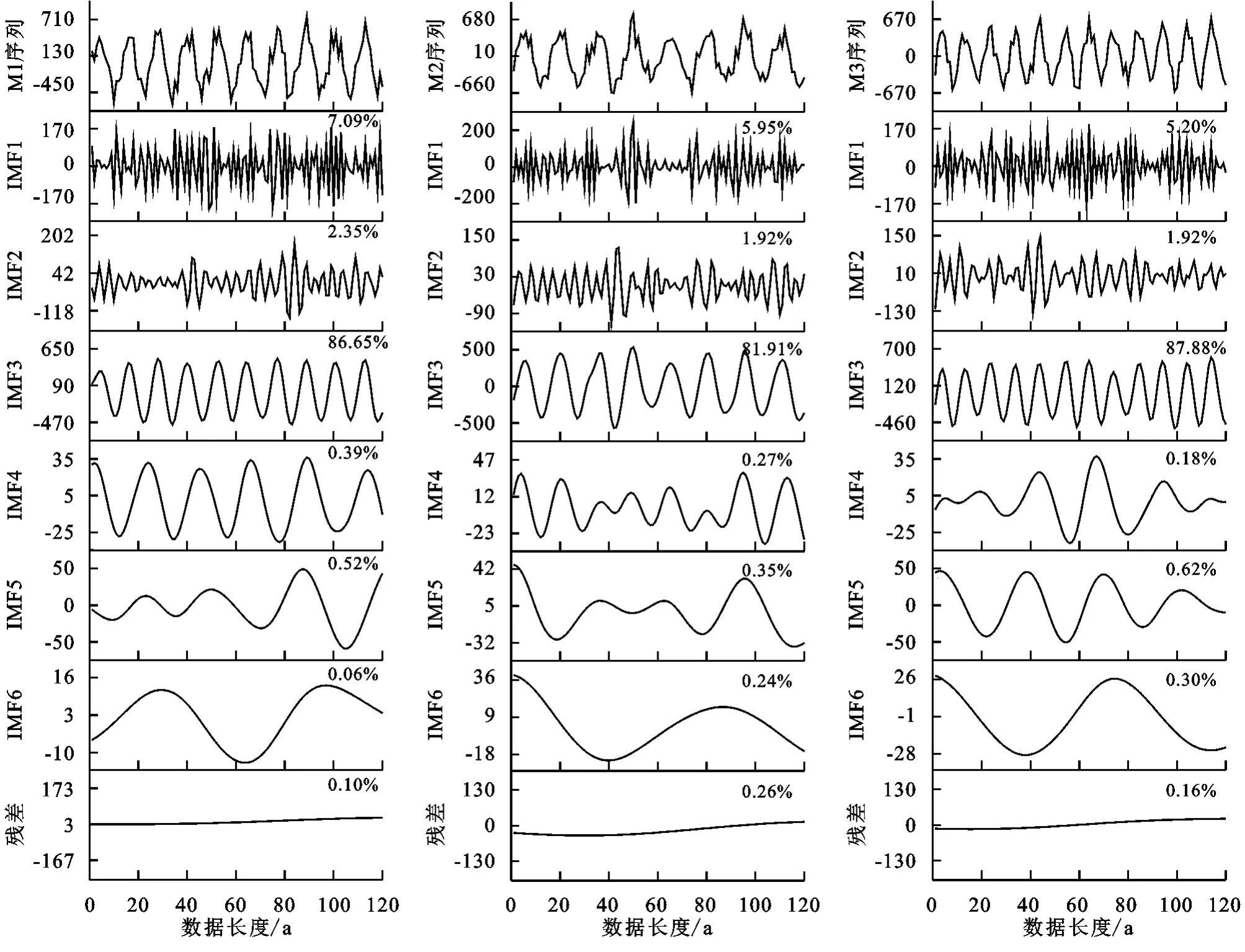
图5 基于第2组人工序列M1,M4,M5使用HHT分解得到的固有模态函数(IMF1-6)和残差项Fig.5 The intrinsic mode function(IMF1-6)and residual term decomposed by HHT based on the first set of artificially generated sequences M1,M4 and M5
图6A 和6B分别为人工序列采用不同延拓方式(对称和周期延拓)获取到的小波方差以及对应的小波实部。小波方差反映了时间序列的波动能量随时间尺度的分布,根据峰值的个数可以确定时间序列中存在的主周期数量;小波实部则能反映出不同特征时间尺度信号在不同时间上的分布和相位等信息。结果表明:(1)当采用对称延拓的小波分析时,M1,M2和M3的小波方差最大值均于19处取得,识别出的周期均为12.6 a;M4和M5的小波方差最大值分别于23,15处取得,识别出的周期为16 a和10.4 a,对周期的识别总体上相对偏大(表1)。(2)相较于前者,采用周期延拓的小波分析识别出的M1-M5周期与人工序列的预设周期基本一致,分别为12.2 a,12.2 a,12.2 a,14.9 a以及10.1 a。
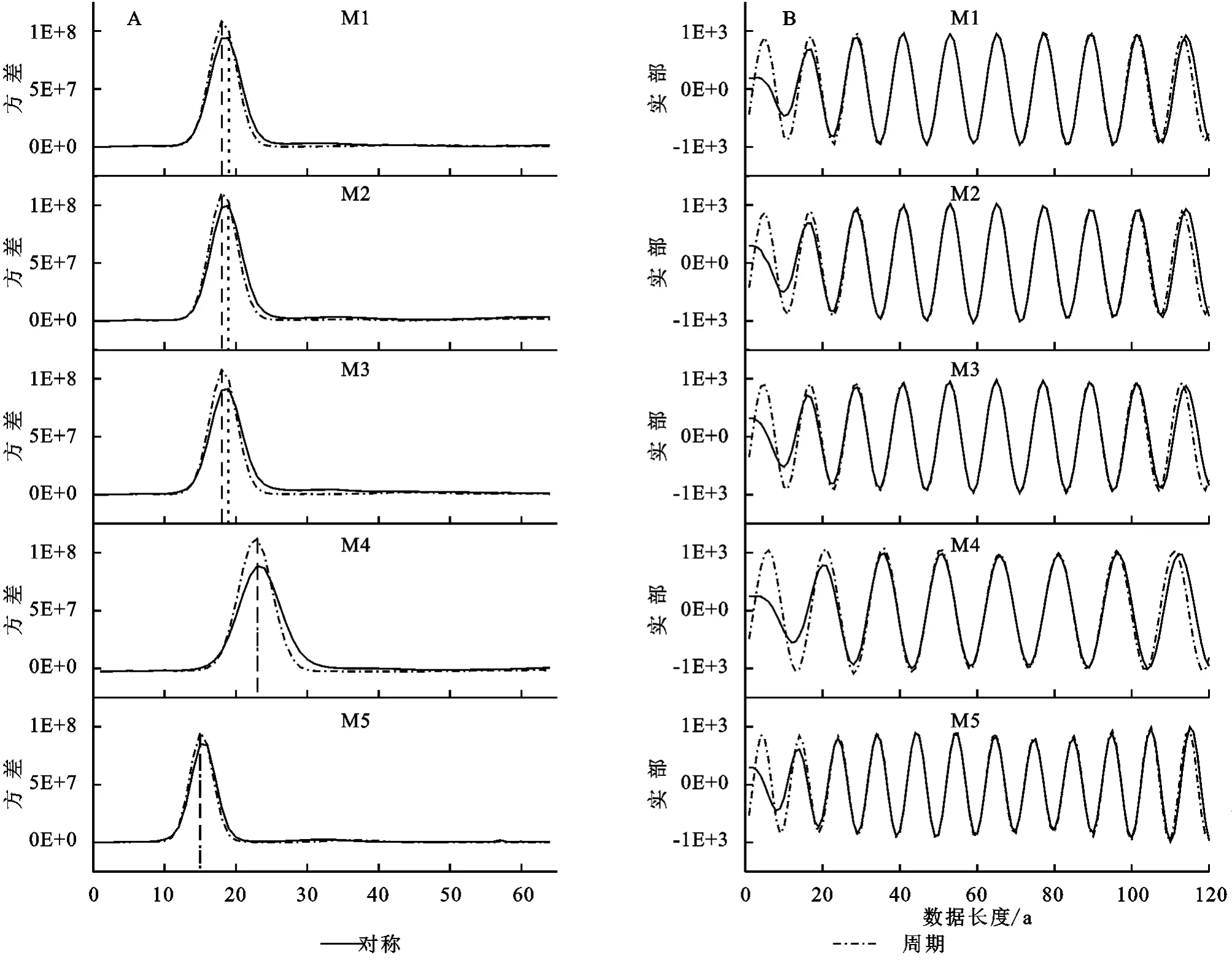
图6 基于人工序列使用小波分析方法得到的小波方差(A)和小波实部(B)图Fig.6 Wavelet variance(A)and wavelet real part(B)obtained by using wavelet analysis method based on artificially generated sequence
为进一步检验各方法的周期结果与人工序列预设周期的精度差异,进行了配对样本t检验。统计结果表明:HHT 的显著性为Sig.=0.142>0.05,采用周期延拓的小波分析的显著性为Sig.=0.109>0.05,两者的周期识别结果与预设周期一致,不存在显著差异,且HHT 的周期准确性要略高于周期延拓的小波分析;相比之下,采用对称延拓的小波分析的显著性为Sig.=0.003<0.05,识别出的周期结果偏大,与预设周期存在显著差异(表3)。总的来说,H HT 与小波分析(周期延拓和对称延拓)相比,周期识别精度最高。

表3 配对样本t检验结果Table 3 Paired sample t test results
2.2 实测序列分析
HHT 将毛乌素沙地11个降雨站点的时间序列分解为5个IMF和1个残差分量。IMF的方差贡献率计算结果表明,11个站点的IMF1和IMF2方差贡献率最大,两者贡献了原始序列41.36%~74.93%的方差(图7)。其中,毛乌素东南部3 个站点S1(图7A)、S4(图7D)和S5(图7E)IMF2的振幅均在2000年之后表现出了明显增加,这表明这3个站点的降雨波动经历了平缓—剧烈的过程,且当前正处在降雨量变化较为强烈的阶段,年际变化不稳定。而其余站点主周期对应的IMF 振幅总体较平缓,无异常波动。此外,图7L还展示了11个站点1982—2020年的降雨趋势变化特征:西部站点(S6,S7和S9)的残差项低于200,变化趋势不明显;中部站点(S3,S8和S10)的残差位于300左右,有轻微上升趋势;而东部站点(S1,S2,S4,S5 及S11)的残差项位于300~500 之间,上升趋势明显。总体上来看,残差项表现为:西部<中部<东部,与前文所述的降雨量空间分布格局一致。通过对实测降雨的分析发现,H HT 方法不仅可以了解降雨量随时间的波动情况,还能通过残差项准确把握序列的变化趋势。
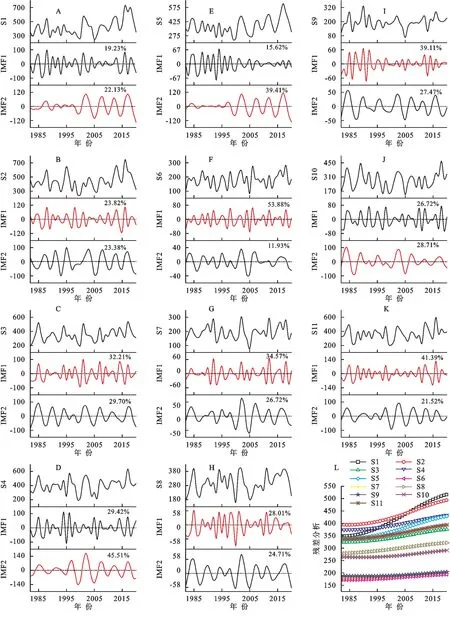
图7 基于实测降雨序列使用HHT得到的主要固有模态函数(IMF1-2)和残差项Fig.7 Main intrinsic mode function(IMF1-2)and residual term decomposed by HHT based on measured rainfall series
表4展示了HHT和小波分析计算出的各站点主周期。(1)HHT结果表明:11个站点的第一主周期范围为2.7~5.5 a,第二主周期为2.8~5.6 a。(2)小波分析(对称延拓)的结果表明:11个站点中的4个站点识别出了3个主周期(S2,S6,S9和S10),3个站点识别出了2个主周期(S1,S3和S11),剩余4个站点仅识别出了1个主周期(S4,S5,S7和S8),且站点第一主周期范围为4.6~13.0 a。(3)而小波分析(周期延拓)的结果表明:除S10识别出2 个主周期外,其余站点均识别出了3个主周期,且第一主周期在5.6~21.0 a之间,第二主周期在5.6~19.5 a之间。图8A从3种方法识别出的周期来看,采用不同延拓方式的小波分析得出的周期结果在空间分布上无明显规律,无论是采用对称延拓还是周期延拓,绝大多数站点的小波分析主周期依然偏大,且在空间上差异大,尤其在相邻站点出现了异常,如S8与S10的对称延拓结果,以及S5,S2与S1的周期延拓结果。而H HT可以识别出全部站点相同数量的主周期,这主要是因为MEMD克服了多变量数据中的模式对齐问题,能获取多个站点的共同尺度,更适合区域尺度降雨周期的求解。

表4 基于实测降雨序列使用HHT和小波分析得到的主周期表Table 4 The main periodic table obtained by using HHT and wavelet analysis based on the measured rainfall series
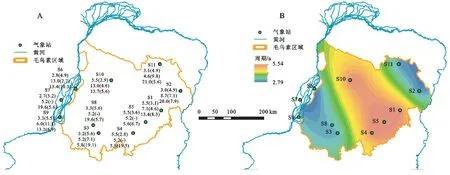
图8 基于实测降雨序列的主周期空间分布Fig.8 Spatial distribution of rainfall main period based on measured rainfall series
此外,采用H HT 还发现毛乌素沙地的降雨主周期在空间上具有明显的区域差异,即腹地区域的降雨主周期大于沙地边缘地区。由图8B 可知,毛乌素腹地站点(包含S1,S4,S5,S10)的第一主周期均为5.5 a,第二主周期在2.8~3.6 a之间;而沙地边缘或临近黄河站点的降雨序列第一主周期为2.7~3.3 a,第二主周期在4.9~5.6 a之间。
3 讨论
本研究利用人工序列和实测降雨序列,对H HT和小波分析在求解区域尺度降雨周期演变特征的适用性上进行了测试、对比和分析。人工序列的结果可为周期识别的准确性提供依据,而实测降雨数据为研究区域多尺度的周期演变提供应用实例,两者结果相辅相成。
在测试对比中,HHT 能准确识别人工序列的周期,同时也能很好地反映数据的趋势变化;而相较于对称延拓,采用周期延拓的小波分析能更准确地识别人工序列周期,并能有效减小端点效应造成的周期识别误差。造成上述现象的原因主要有以下两个方面:一是小波分析相较于其他分解方法(经验模态分解EMD,变分模态分解VMD 等),受Heisenberg测不准原理影响,只能分析出近似周期,缺乏自适应性[22];二是在本研究中,人工序列的预设周期是以正弦函数为基底,有明显规律波动,这使得序列端点处按照周期延拓更加合理,由此得出的结果也几乎和预设周期一致。证实了不同延拓方式的选取在一定程度上会导致数据周期结果失准,这也从侧面论证了若要使用小波分析得出准确的周期结果,许多参数选取(如小波基、延拓方式等)都需要慎重考虑。除了上文阐述的主要原因外,本研究还发现当小波方差含有多个主峰或主峰不明显时,很难准确识别主周期下的周期尺度,这可能也是小波分析周期偏大的主要原因[23]。总的来说,测试分析的结果表明相较于传统的小波分析,HHT 因其自适应性分解能力使之在水文时间序列的周期识别和趋势检测方面具有较为广阔的应用前景。
在实例应用中,HHT 和小波分析(对称延拓)识别出的周期结果与前人的研究基本一致,而小波分析(周期延拓)则偏差较大[24-25]。与人工序列不同,造成小波分析(周期延拓)识别效果不佳的原因可能是因为实测降雨序列往往没有明显的波动规律,常呈现多时间尺度、多频率的变化特性,致使周期延拓会以整个时间序列为单位进行延展,进而忽略序列内部蕴藏的短时间尺度周期。相比之下,H HT 和小波分析(对称延拓)识别出的降雨主周期也存在一定差异,主要体现在两方面:一是H HT 识别出毛乌素沙地所有站点均有2个降雨主周期;而小波分析(对称延拓)得出的各站点降雨主周期数量不等,在1~3之间。二是从计算结果的数值来看,HHT 计算得到的毛乌素沙地降雨主周期平均为3.9 a,且各站点的主周期较为接近;而采用对称延拓的小波分析得到的降雨主周期平均为7.1 a,但不同站点之间差别较大,且个别站点还高达10.3 a(S6)。这些差异主要依赖于MEMD方法在寻找多变量共同尺度上的优势,这不仅有助于实现区域尺度上降雨周期的求解,同时也能避免区域尺度上因个别站点的极端变化导致的周期失准问题[26-27]。此外,本研究还发现毛乌素东南缘站点(S1,S4和S5)的降雨量波动在2000年后变得更为剧烈,这可能是这些区域在2000年后大降雨事件频发所导致的[28]。在空间分布上,毛乌素腹地站点的降雨主周期大于边缘站点,这可能与这些站点的地理位置有关,这些区域相对远离黄河、植被盖度较低且土地利用类型较为单一,局地水汽循环更新缓慢,从而导致区域上存在明显的周期差异。并且贾路等的研究[29]也表明了大气环流和地形因素对水汽输送过程的影响也是改变区域降雨周期的重要因素。总的来说,毛乌素沙地的降雨周期演变差异是复杂下垫面条件下不同纬度大气环流连贯性调整的结果[30]。
虽然本研究展示了HHT 在周期识别和趋势检测方面的性能,可为水文时间序列的多尺度周期特征分析以及非线性趋势检验提供一定的参考。但同时,本研究仅以11个站点39 a的降雨序列为实例,从应用角度对比分析了HHT 方法和采用不同延拓方式的小波分析在区域降雨周期演变特征上的差异,对方法性能的评价可能还存在一些局限性。此外,针对降雨过程在区域尺度上呈现出的复杂性和不确定性,可以考虑在之后的研究中将“分解—预测—重构”的耦合思路用于建立混合预测模型,利用分解技术将数据分解为多个相对平稳的时间序列,不仅能有效降低降雨的复杂度和不确定性,而且还能使模型更好地捕捉水文序列的变化特征,之后可以再结合机器学习或深度学习技术,进一步提高水文预测的精度。目前,HHT 方法在水文领域的应用仍处于初步探索阶段,尚需在后续研究工作中进一步深化。
4 结论
本研究基于2组已知成分的人工序列对HHT方法和小波分析在周期准确性上进行了测试对比,并基于毛乌素沙地1982—2020年11个站点实测降雨序列进行多尺度周期分析,现得出以下主要结论:
(1)对于波动规律较为明显的人工序列,HHT的周期识别精度最高。经统计检验证明,HHT 与小波分析(周期延拓)的周期识别结果与预设周期一致,不存在显著差异;而小波分析(对称延拓)结果大于预设周期。
(2)对于实测降雨序列,H HT 和小波分析(对称延拓)可以较为准确地识别降雨周期特征,而小波分析(周期延拓)则有较大偏差;小波延拓方式的选取会影响实测降雨序列的周期识别结果。
(3)HHT对区域降雨序列多尺度分析有很好的适用性,该方法计算出的降雨主周期存在明显的区域差异:沙地腹地站点的降雨主周期(5.5 a)远大于沙地边缘站点的主周期(2.7~3.3 a);且沙地降雨量在时间上呈明显的上升趋势,在空间上由东到西逐渐减少。
(4)本研究认为H HT 相较于小波分析,因其自适应性特征,无需考虑众多参数的选取,在保持精度的同时可以提取更多水文信息,在降雨序列多尺度分析上更具优势,因此具有重要的实际应用价值。

