基于Morris和Sobol法的茶园地上部生物量与氮磷流失模拟敏感性分析
叶志成,张莉莉,廖凯华,朱青,赖晓明,郭长强
(1.中国科学院南京地理与湖泊研究所流域地理学重点实验室,南京 210008;2.中国科学院大学南京学院,南京 211135)
基于过程的生物地球化学模型作为模拟一系列生态现象和生态过程的有效工具,对于研究土壤-作物系统中的物质运移和元素转化等过程有重要意义。相比于有限的点位观测和大田试验,生物地球化学模型具有可重复、耗时短的优点,可以有效节约人力和物力成本。但是为了模拟生态系统中的复杂过程,模型往往被构建为一个复杂的动态系统,其中包含大量的输入参数,而这些参数均具有不同程度的不确定性,这种不确定性会严重影响模型输出的准确性。因此,通过敏感性和不确定性分析识别模型输出不确定性的来源及影响程度,被认为是应用模型的先决条件[1]。通过敏感性分析可以识别不同模型参数对于模型输出的影响程度,对于影响程度较小的模型参数采用经验值,着重研究分析影响程度大的模型参数,从而提高模型率定的效率与精度[2]。不确定性分析结果显示出对模型输出结果误差的估计。这两种分析方法往往结合使用,以提升模型结果的可靠性。基于过程的DNDC模型由于其对土壤碳氮迁移过程的准确追踪和模型的易操作性,在中国各地都得到了广泛应用,其敏感性也得到了广泛检验。但是前人的研究领域大多集中在农田[3]、果园[4]和湿地[5]等,很少有研究关注DNDC模型在东南湿润区坡地茶园模拟领域的效果,并且前人的研究通常采用单一敏感性分析方法进行敏感性分析,很少结合多种方法。当选用的敏感性分析方法不同时,预测的参数敏感性也会发生变化。在中国,茶树作为一种重要的经济作物被广泛种植,茶园为了追求经济效益,往往施用大量化肥,导致过量的活性氮磷残留在土壤中,造成土壤酸化和氮磷的大量淋失。同时,前人的研究也发现茶园土壤是亚热带地区乃至全球N2O 排放的重要来源,排放因子远远高于其他农田[6]。近年来,天目湖流域内大量林地被开发为茶园,茶园面积在2017年已经扩大到流域面积的10%[7],由于茶叶种植能带来巨大的经济效益,这种增长可能会一直持续。且流域内茶园多为坡面种植,结合流域土壤土层较薄的特点,在降雨事件发生时存在极高的面源氮磷流失风险。实地调查表明,由于茶园的迅速扩张,已经导致天目湖水质急剧恶化[8]。因此,深入研究茶园土壤的氮磷迁移、转化过程以及土壤与作物之间的耦合关系具有重要的现实意义。本研究利用定性(Morris法)和定量(Sobol法)两种敏感性分析方法和基于蒙特卡洛的不确定性分析方法,基于流域内径流小区实测数据,确定DNDC模型的输出结果(茶园的地上部生物量、氮磷淋失量、水分渗漏量以及N2O,NO 和NH3排放量)对土壤、地形和作物参数的全局敏感性,并对其进行排序确定每个模型输出的最敏感参数,探讨敏感参数出现的原因,并量化每个输出结果的不确定性,为实现茶园土壤氮磷运移转化过程的准确模拟提供基础。
1 材料与方法
1.1 站点概况及参数选择
本研究以中国科学院南京地理与湖泊研究所“天目湖流域生态观测研究站”(北纬31°16′8″,东经119°24′32″)为例,基于站点观测到的气象数据、土壤数据和农业管理数据进行分析。该地区位于天目湖流域,气候为亚热带季风性气候,多年平均温度17.3℃。多年平均降水量为1 165.3 mm,大约65%的降水集中在6—9 月份。试验区位于低山丘陵区(高程<200 m),坡面为直型坡,平均坡度9°,接近天目湖流域茶园平均种植坡度,坡面土壤类型为黄棕壤,渗透能力强,难以形成地表径流,大量水肥以壤中流的形式输移[9]。坡上等高种植茶树,修剪、除草等管理措施均为当地常规管理方式,据调查流域内茶园一年施肥两次,合计折氮量为400~600 kg/hm2,折磷量为100~150 kg/hm2。茶园坡地小区的坡顶、坡中和坡底分别设有土壤水样监测点,在土层底部放入土壤渗漏液采集器,从2019年12月开始以大约每月一次的频率采集土壤水分渗漏液,测定其溶解性总氮浓度(DTN)、溶解性总磷浓度(DTP)、硝态氮浓度(NO-3-N)和正磷酸盐浓度(PO3-4-P)等数据。每年的3月和11月各施肥一次,肥料累计折氮量和折磷量分别为306.75,106.08 kg/hm2,并在3月追肥后对茶树进行采摘和修剪,测定所采茶叶的水浸出物、茶多酚和游离氨基酸等指标和干茶重。
模型模拟输入的气象数据来自观测站实地测量数据,选取2018—2020年3年的逐日最高气温、最低气温和日降雨量输入模型(图1),模型最后的输出值取3 a的平均值。所需的土壤和地形参数主要来源于田间试验的实测值,使用土钻采集坡地小区不同深度土壤样品,风干后测定其田间持水量、质地、容重等。作物参数选取DNDC模型中的默认值。各参数的取值范围为标准值±10%,并假定所有参数的分布为均匀分布(表1)。

表1 选取的DNDC模型参数及取值范围Table 1 Selected parameters and their value ranges in DNDC model

图1 2018-2020年天目湖流域气象因子时间变化Fig.1 Temporal variation of meteorological factors in Tianmu Lake Basin from 2018 to 2020
1.2 DNDC模型
DNDC(DeNitrification-DeComposition)模型是一个基于过程的生物地球化学模型,其核心是模拟农业生态系统中碳氮等元素的运移转化等过程[13],在预测农作物产量、农田土壤碳动态、化肥对水体污染及农田温室气体排放等方面得到了广泛应用。模型由两部分组成,第一部分包括土壤气候、作物生长和有机物分解3个子模型,通过气候、土壤、作物和农业管理措施4个驱动因素来模拟土壤环境条件(温度、湿度、p H 值、氧化还原电位等)、作物生长(作物对氮磷和水的吸收量和作物根、茎、叶和籽粒的生长量)和土壤碳氮库的动态变化〔CO2的产生、NH+4-N,NO-3-N 和土壤有机碳(SOC)浓度剖面〕;第二部分由硝化、反硝化和发酵子模型组成,有机物分解产生的碳氮磷等元素被输入这3个子模型中,进而模拟出氮磷的淋失量以及N2O,NO,N2,NH3和CH4的生产、消耗和排放。
1.3 敏感性分析方法
敏感性分析方法主要分为局部敏感性分析和全局敏感性分析两种,局部敏感性分析通过逐一改变单个参数的值来分析单个参数变化对模型输出变量的影响,适用于线性或接近线性的模型,而全局敏感性分析则充分考虑了多个参数变化及参数之间的交互作用对模型输出变量的影响,适用于耦合过程较多的非线性模型。全局敏感性也可以分为定性和定量两种,定性分析主要评价各参数对模型结果影响的相对大小,方法包括Morris参数筛选法[14]和多元回归法等;而定量方法则可以给出每个参数对模型结果的贡献率,包括基于方差的Sobol法[15]和扩展傅里叶幅度检验法。
1.3.1 Morris法 Morris法是一种是在局部敏感性分析方法一次一个变量法(one-at-a-time method)基础上改良而成的一种全局敏感性分析方法,其原理是通过一次只改变一个参数的取值方法轮流计算参数的基本效应值(EEi),计算公式如下:
式中:EEi为第i个单位的基本效应值;f(X1,X2,…,Xi+Δ,…,Xk)为参数变化后模型的输出;f(X1,X2,…,Xk)为参数变化前模型的输出;Δ为参数的变化量。
Morris敏感性指数的计算公式为:
式中:平均值μi越大代表参数Xi对模型输出的影响越大,即敏感性越强;标准差σi则代表参数之间交互作用的强弱,σi值越高,交互作用越强[14]。
1.3.2 Sobol法 相对于定性的Morris筛选法,基于方差的Sobol法可以定量求解复杂非线性模型中各个参数及参数间相互作用所产生的敏感性,其主要思想是将模型函数分解成多项递增项之和,通过随机采样计算参数对模型响应的总方差(V)及各项偏方差(V1,Vij,…,V1,2,…,n),求得各参数的灵敏度。
Sobol敏感性指数的计算公式为:
一阶敏感性指数
二阶敏感性指数
总敏感性指数
式中:一阶敏感性指数Si代表参数Xi的变化对于整个模型方差变化的贡献,用于定量描述参数Xi对模型输出的影响;二阶敏感性指数Sij代表参数Xi和Xj之间的相互作用对于模型输出方差产生的影响;以此类推,总敏感性参数STi为各阶敏感性指数之和,不仅反映了参数单独变化产生的影响,也考虑了参数之间的相互作用对输出结果的影响,更详细的计算过程请参考Sobol[15]的论文。
1.4 分析方案与数据处理
本研究基于Morris法和Sobol法对茶园小区的茶树地上部生物量、氮磷淋失量、水分渗漏量及N2O,NO和NH3排放量进行敏感性和不确定性分析,选择8个土壤参数、1个地形参数和11个作物参数输入模型。敏感性和不确定性分析主要借助基于蒙特卡洛的敏感性分析软件Simlab完成,本文的敏感性分析方案借鉴Campolongo等[16]提出的一种兼具准确性和计算成本的方法,具体方案如下:(1)对所有输入参数采用Morris法进行分析,模型运行次数为r×(k+1)次,其中r取4,k取19,共运算80次。(2)计算敏感性均值μi和标准差σi,对计算出的μi进行分类,取的参数为Morris敏感参数。(3)对Morris法得到的敏感参数进行Sobol法分析,模型运行次数为N×(2k+2),其中N取32,k取11,共运算768次,得出一阶敏感指数Si和总敏感性指数STi,将STi>0.10作为Sobol敏感指数的取值标准。(4)对各个输出结果的μ值与STi值进行皮尔逊相关性分析。基于Sobol法产生的768次模拟,得出各输出结果的概率统计分布并量化其不确定性。本研究所用的各项数据采用Microsoft Excel,SPSS和Origin作数据处理与作图分析。
2 结果与分析
2.1 Morris法结果
Morris法的分析结果如图1 所示,位置越靠右的模型参数敏感度越高,位置越靠上的模型参数与其他参数的交互作用越强。对于地上部生物量,土壤参数的敏感度极低,而作物参数P1(最大籽粒产量)和P2(成熟时籽粒占总生物量之比)的μ值远远大于其他参数,与其他参数交互作用较强。在模型模拟过程中,作物参数P1和P2决定了在最佳的生长条件下籽粒的最大生物量以及成熟时籽粒占全株生物量的比例,是影响地上部生物量的主要参数(图2A)。
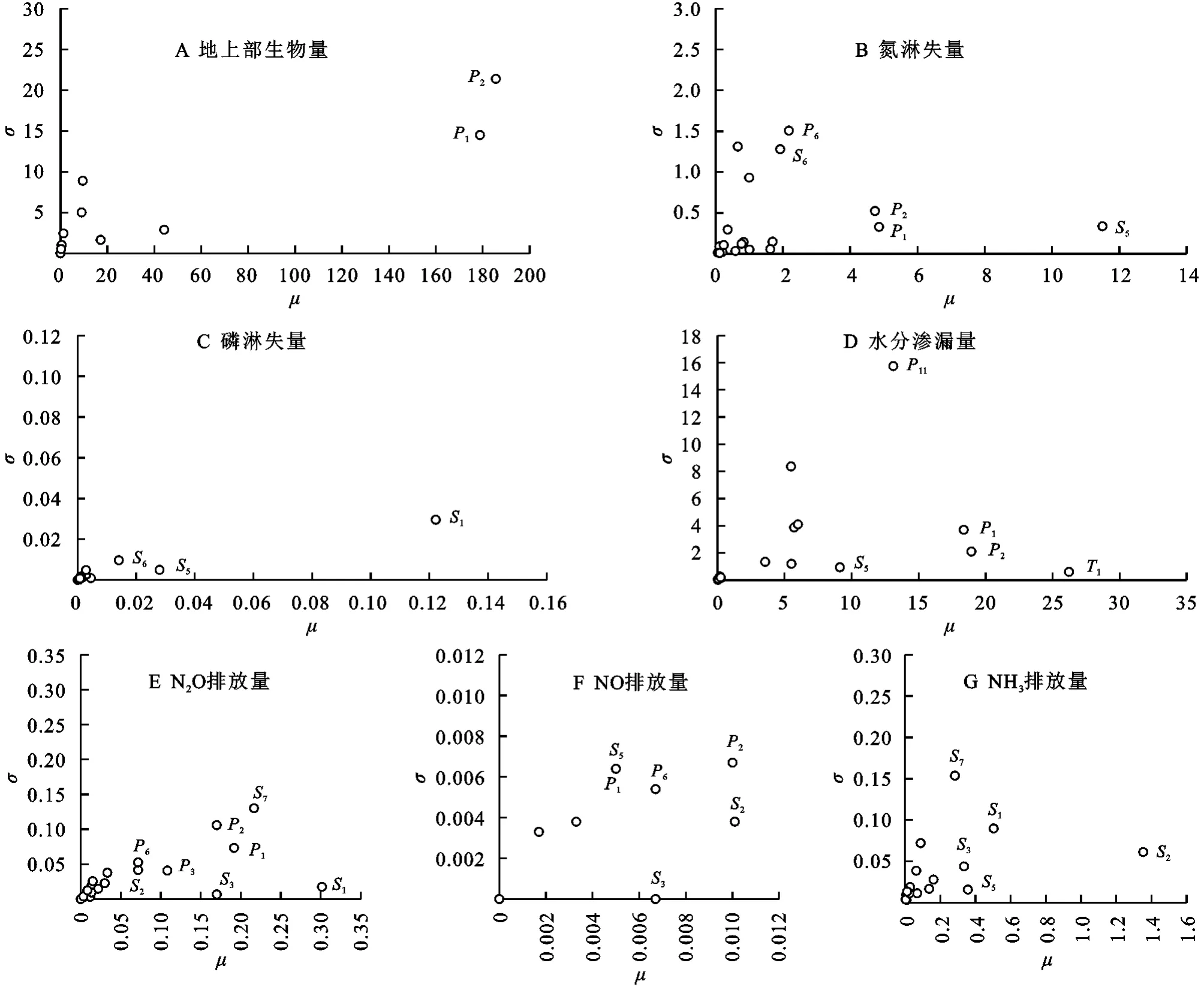
图2 基于Morris法的DNDC模型敏感性分析结果Fig.2 Sensitivity analysis based on Morris method for DNDC model
DNDC模型中氮淋失量主要由土壤中的硝态氮浓度、黏粒含量和水分渗漏量3种因素共同作用,并且在模拟中黏粒含量对于氮淋失量存在指数级影响,因此试验结果显示S5(黏粒含量)是最主要的影响因素(图2B)。作物参数P1,P2会影响植物的日需氮量,从而改变土层中的氮浓度。P6(叶碳氮比)和S6(孔隙度)也通过影响植物的需水量和土壤水分活动间接对氮素淋失产生影响,交互作用较强;对于磷淋失量,土壤参数S1(容重)的μ值远高于其他参数,是影响磷淋失量的主要参数。在模型中,淋失过程只考虑溶解态磷,土壤容重通过影响土壤的吸附解吸以及有机态磷和溶解态磷之间的转换过程影响磷淋失量(图2C);S8(坡度)是影响水分渗漏量的最直接因素(图2D),DNDC通过每日作物的需氮量和需水量来计算当日的蒸腾量,因此P1,P2,P11(需水系数)和S5也间接影响模拟的水分渗漏量,其中P11与其他参数的交互作用较强。
由于N2O和NO都是硝化反应和反硝化反应的中间产物,产生量的比例取决于反应的进行程度,因此二者的敏感参数存在相似性,其中S1,S7(SOC),P1,P2,S3(田间持水量)均为N2O和NO排放量的敏感参数,但是影响程度不同(图2E,2F)。这是由于不同的环境因子对硝化反硝化过程的制约程度不同,其中影响N2O排放量的主要参数为S1,影响NO 排放量的主要参数为S2(p H)和P2。同时,S2也是影响NH3排放量的主要参数,这是由于土壤中的酸碱性对于各土层的NH+4-N浓度影响较大,进而影响NH3的产生。
2.2 Sobol法分析结果
相比于Morris分析结果,Sobol法可以更直观地观察出参数的敏感性大小及其相互作用强弱(图3)。参数的总敏感性指数与一阶敏感性指数之差即为该参数与其他参数的交互作用对模型输出项的影响程度。对于地上部生物量(图3A),敏感参数与Morris法分析结果相似,P1和P2仍是影响地上部生物量的主要参数,总敏感性指数分别为0.27,0.29,但是与Morris法不同的是,Sobol法的结果显示S5对地上部生物量也具有很强的影响,总敏感性指数为0.24,并且与其他参数的相互作用程度较高;对于氮、磷淋失量、水分渗漏量和NH3排放量,Sobol法分析结果也与Morris法分析结果相似,影响氮淋失量的主要参数是S5,影响磷淋失量的主要参数是S1,影响水分渗漏量的主要参数是S8,影响NH3排放量的主要参数是S2,总敏感性指数分别为0.63,0.46,0.28,0.42。

图3 基于Sobol法的DNDC模型敏感性分析结果Fig.3 Sensitivity analysis based on Sobol method for DNDC model
但对于N2O 排放量和NO 排放量,结果略有不同。Sobol法分析结果显示参数S1,S3,P1,P2和S7对N2O 排放量的总敏感性指数较为接近,介于0.11~0.13,其中S7的总敏感性指数略大,为0.13(图3E);影响NO 排放量的主要参数是S2,参数S1,S3,S5,P1,P2的总敏感性指数介于0.09~0.12,对于输出结果的影响程度也较高(图3F)。
2.3 Morris法与Sobol法敏感性分析结果比较
对Morris法和Sobol法所得出来的敏感参数,分别按照其敏感性指数(μ和STi)的大小从左到右进行排序并对两种方法得出的参数敏感度顺序做相关性分析,得出的结果见表2。除了地上部生物量和N2O 排放量,Morris法与Sobol法得出的最敏感参数均一致。对于地上部生物量、氮淋失量、磷淋失量、水分渗漏量和NH3排放量,参数敏感度顺序相关性极高,平均为0.90,但N2O 排放量和NO 排放量的参数敏感度顺序相关性略低,平均为0.76,总平均相关性为0.86。

表2 Morris法与Sobol法敏感参数排序和相关性比较Table 2 Morris method and Sobol method for sensitive parameter sequencing and correlation comparison
2.4 不确定性分析结果
上述结果表明,随着模型输出的不同,各参数的敏感性也不相同。为了进一步分析DNDC模型模拟的茶园地上生物量和氮磷流失等输出结果,有必要进一步识别DNDC 模型输出结果的误差,量化各输出结果的不确定性。基于Sobol法建立的768次模拟结果,对其进行统计分析,结果见表3。其中,磷淋失量的变异系数值最大,为43.84%,说明模拟结果的离散程度较大,误差较大。水分渗漏量的变异系数值最小,为2.36%,说明模拟的准确度较高,误差较小。

表3 模型各输出统计结果Table 3 DNDC model outputs statistical results
3 讨论
在DNDC模型中,作物参数主要控制生物量的增长和分配以及影响作物与土壤的物质交换。P1是决定作物日潜在生长量的关键参数,对于作物的生物量大小起到最主要的控制作用。P2代表作物成熟时籽粒的生物量占总生物量之比,影响着生物质在籽粒、叶、茎和根之间的分配。在模型模拟的过程中,当模拟的作物还在生长期时,每日增加的生物量只在叶、茎和根中根据比例分配,而当作物的生长指数(累计积温占总积温的比例)超过设定的生长期比例时,新增的生物量全部分配到籽粒中[16]。因此,P2对于地上生物量大小具有很强的影响作用。本研究所采用的两种敏感性分析方法都显示P1和P2是影响作物地上生物量的主要参数。茶树作为一种叶芽收获作物,在采摘后茎叶留存率较高(本文设置为0.9),因此在收获后会进行人工修剪(本文设置修剪比例为0.4),产生的大量凋落物继续输入土壤,并且作为多年生作物,其根系与土壤的物质交换活动频繁,对土壤p H 值、有机碳含量等影响显著。在DNDC 模型中,作物的生物量和碳氮比决定了其养分吸收量和蒸腾量,作物的根系呼吸以及产生的凋落物也会影响土壤中的有机物分解与硝化反硝化过程[17]。本研究的结果也表明作物参数P1,P2和P6对模型输出氮淋失量、水分渗漏量、N2O 和NO 排放量均具较高的敏感性。
相比于作物参数,土壤参数对土壤中的各种过程具有更直接的影响。前人的研究表明土壤的黏粒含量与土壤的持水保肥能力息息相关[18],黏粒含量高的土壤养分保持能力较好,可以在一定程度上减少氮的淋失量,而黏粒含量较低的砂质土壤中的氮素较易流失。另外,DNDC模型主要采用土层硝态氮浓度、水分渗漏量及黏粒含量等来模拟预测氮淋失量[19],因此本文的分析结果也显示土壤的黏粒含量是影响氮淋失量的最主要参数。DNDC 模型中的磷素在土壤中的平衡主要依赖于土壤的吸附-解吸过程,研究显示在p H 值为4~10的土壤中,吸附过程是控制溶解态磷的主要作用[20],土壤对磷的吸附能力受到土壤胶体、土壤团聚体和黏粒含量等因素的综合影响,而这些因素与土壤容重密切相关,因此成为影响磷淋失量的最主要参数。正是由于模拟磷淋失过程中涉及到的参数众多,模拟的磷淋失量的不确定性也较大。坡度在模型中被用来调节降雨时的地表径流量,同时也对地下渗漏量产生显著影响,本文的结果也显示S8是对水分渗漏量影响最大的参数。DNDC模型中的硝化与反硝化子模型模拟N2O,NO 和NH3三种气体的输出,作为土壤氮循环的重要过程,许多研究对影响硝化与反硝化过程的因素进行了深入研究。朱兆良等[21]研究发现在酸性到微碱性的p H 值范围内,硝化作用和p H 值呈显著正相关,而Li等[22]研究结果显示当土壤p H 值大于8.5或小于6.5时,土壤的硝化活性受到抑制。与农田土壤相比,茶园土壤的p H 值较低,这是由于茶树为喜铝作物,其根际效应和富铝凋落物的输入,会使土壤中的铝元素富集,导致茶园土壤偏酸。本文的结果显示,土壤p H 值是影响NO 排放量的主要参数,而对N2O 排放量影响不明显,这是由于模型在对反硝化速率的计算过程中,当p H 值大于5.25时,p H 值对NO 反硝化速率的影响系数会显著加大,而对于N2O 反硝化速率,p H 值需大于6.25[23]。本文设置的p H 值范围为5.769~7.051,在此范围内p H 值对于NO 反硝化速率的影响程度大于对N2O反硝化速率。NH3的挥发来源于土壤中的NH+4-N 的转化,p H 值对于土壤中NH+4-N 浓度影响显著,因此是影响NH3排放量的主要参数。SOC含量同样对土壤的硝化与反硝化过程存在影响,一方面土壤中的有机物可以为参与硝化或反硝化过程的微生物提供能量并且可以通过矿化分解为反应提供底物,从而促进硝化或反硝化过程,另一方面由于有机物周围作为土壤呼吸的“热点”,有利于形成厌氧环境,进一步促进反硝化作用[24]。研究表明,由于茶园的高施肥量,土壤中的SOC 含量也高于同一地区的稻田和林地[25-26],SOC的增加刺激了土壤中的微生物活动,促进N2O 和NO 的形成。Bollmann等[27]研究表明,由于黏粒含量高的土壤保水能力较强,气体扩散率较低,有利于形成厌氧环境,因此黏粒含量对于土壤的反硝化势有着显著的正效应。这与本文的研究结果也一致,尽管顺序不同,上述影响硝化反硝化过程的因素均为N2O,NO 和NH3排放量的敏感参数。同样,这些参数自身的不确定性和模拟过程的不确定性相互叠加,导致模拟值的不确定性偏大。
以不同国家(法国、希腊、意大利、葡萄牙和西班牙)的5 个水稻区为例,Confalonieri等[28]应用Morris与Sobol两种方法对WARM 模型模拟出的水稻产量进行敏感性分析,研究发现模型输出对参数的敏感性在不同地点或气候中会产生变化,并且两种敏感性分析方法的敏感参数也不一致,因此当模型在新环境中使用时,重新检测参数敏感性是必不可少的。但是对于同一研究区的敏感性分析结果,许多研究发现不同的敏感性方法往往表现出相似的排序方案。DeJonge等[29]利用Morris与Sobol两种方法对CERES-Maize模型进行敏感性分析发现Morris方法的μ和Sobol方法的STi之间的r值高达0.93,表现出相当高的相关性。Confalonieri等[30]基于意大利北部稻田对WARM模型应用多种敏感性分析方法,包括Morris法、3种基于回归的方法和两种基于方差的方法,结果发现这几种方法均能提供相似的敏感性排序。本文的研究结果显示,模型输出结果的总相关性为0.86,略低于Qin等[31]的结果,但是高于Campolongo 等[16]的结果。其中,地上部生物量、氮淋失量、磷淋失量、水分渗漏量和NH3排放量,敏感性参数的相关性较高,平均值为0.90,但是N2O 和NO 两组的相关性略低,分别为0.79,0.73。从图2E—F可以看出,各个参数之间的相互作用程度和非线性程度较高,而Morris法对于识别各参数间的交互作用和非线性效应效果较差,导致两种方法的相关性较低。
两种敏感性分析方法各有利弊,Sobol法可以量化各参数对模型输出的贡献率,得到的结果更加有可信度,但是运算成本较高,Morris法所需要的模型运行次数较少,但获取的敏感性分析结果不够精确。因此在具体应用时,可以结合两种方法优势,先应用Morris方法确定敏感参数的范围,再应用Sobol法精确量化,快速准确地筛选出模型敏感参数。根据本文得到的结果,作物参数对于各个模型输出均存在不同程度的敏感性,因此在模型率定过程中,可以先考虑调整重点作物参数,再根据敏感性分析得出的敏感参数顺序,校准土壤参数。
4 结论
(1)敏感性分析结果显示,影响地上部生物量最主要的参数为P2(成熟时籽粒占总生物量之比);影响氮淋失量最主要的参数为S5(黏粒含量);影响磷淋失量最主要的参数为S1(容重);影响水分渗漏量最主要的参数为T1(坡度);影响N2O 排放量最主要的参数为S7(初始土壤有机碳含量);影响NO 和NH3排放量最主要的参数为S2(p H 值)。
(2)Morris法和Sobol法得到的参数敏感度顺序之间的平均相关性为0.86,相关性较高,两者具有一定可替代性。Morris法优在方便省时,Sobol法优在准确全面,将两者结合可以优化敏感性分析过程。另外,不确定性分析结果显示磷淋失量的不确定性最大,变异系数为43.84%;水分渗漏量的不确定性最小,变异系数为2.36%。
(3)在天目湖流域对DNDC 模型进行参数率定时,建议在识别出敏感参数的基础上,先重点校正作物参数,然后校正土壤参数,可以有效提高模型的校正效率。针对不确定性较大的模型输出(如磷淋失量),在未来校正模型时,建议在本文的基础上细化参数的范围,进而进一步提高敏感性分析结果的准确性,降低模型输出的不确定性。未来可以考虑设置不同的气候条件、土壤类型和施肥情景来分析模型的敏感性和不确定性,以提高分析结果的适用范围。
——《2013年中国机动车污染防治年报》(第Ⅱ部分)

