基于BP 算法的中深层同轴套管换热量预测

熊 波，朱冬雪，方朝合，王社教，杜广林，薛亚斐，莫邵元，辛福东

（中石油深圳新能源研究院有限公司，广东深圳 518000）

0 引言

在全球能源危机和环境恶化的背景下，为减少化石能源和碳排放，开发和利用可再生能源已成为全球关注的问题［1］。在绿色可再生能源中，地热能是世界上最丰富的清洁可再生能源之一，具有分布广、储量大、清洁可持续等特点［2］。地源热泵系统是开发和利用地热能最有效的技术，它利用循环流体从地下岩石和土壤中提取热量（或排放热量），为住宅或商业建筑供暖（或制冷），具有高效、节能、无污染、维护简单和寿命长等优点［3-4］。地源热泵系统主要由地埋管换热器、热泵机组和终端空调机组组成，在中深层同轴套管地源热泵系统中，同轴套管换热器是系统的核心部件，其传热性能直接决定了系统能否高效、可持续地稳定运行［5］。因此，对中深层同轴套管换热量进行预测研究，有利于中深层同轴套管地源热泵系统在北方寒冷地区的进一步推广。

近年来，国内外学者对中深层地热传热进行了研究，并取得一定的成果。Kerme 等［6］建立一个传热模型来预测地埋管换热器在换热过程中的瞬态传热过程，并通过动力学计算流体、井壁、注浆和附近地表温度随时间的变化，评价了重要参数的影响；Kumar 等［7］讨论了地埋管换热器和地源热泵系统之间热相互作用的优化结果，得出循环水量对系统性能的影响最大。此外，与传统的U 型管BHE相比，中深层同轴套管换热器系统可有效开发深层地热资源，并具有更大的换热面积。

目前，国内外对于中深层地源热泵同轴套管换热器的研究主要集中于地埋管取热能力、换热优化等方面［8］。Morchio 等［9］通过优化有限差分数值模型来模拟同轴套管，提高了预测流体温度演变的准确性，并应用该模型分析了500～800 m 深层换热器的性能，得出流体温度的演变和内外管道压力损失与管道直径比的影响；Luo 等［10］进一步建立了同轴套管换热器模型，以确定系统中水的最佳流动方向，并研究了钻孔热阻与流出流体温度和提取热量之间的非线性相关性、地热梯度变化对传热的影响；Cai 等［11］基于同轴套管换热器的传热模型给出了热交换的评估图和相关性评价，随着入口流量的减小，管底温度升高，内管热损失也随之增加，在入口流量低的条件下，内管的保温是减少热损失的有效手段，通过减小内管直径以增加流速，也可以有效减少热损失；Huang 等［12］使用同轴套管换热器的数值模型分析和讨论了不同因素对热过程与热性能的影响，结果表明较小的内管半径和较低的内管导热系数会增加热阻，而较大的外管半径和较高的外管导热系数更有利于传热，此外，随着注浆导热系数和孔长的增加，换热器的热性能得到改善；Song 等［13］对同轴套管换热器的传热进行了数值模拟，通过对温度场的分析，得出换热器对围岩土层的影响有限，到下一个采暖期前温度基本可恢复到原始状态，验证了中深孔换热器系统的稳定性；Wang 等［14］通过现场测试和数值模拟研究了深井同轴套管地源热泵系统的传热特性，仿真结果与现场试验数据吻合较好，热泵机组和深井地源热泵系统的平均性能系数分别为6.4 和4.6，而且当循环流体从环形空间流向内管时，管道性能得到改善。

现有大多数关于中深层同轴套管换热系统换热性能的研究主要基于仿真分析，缺乏与实际工程数据的比较［15-16］，主要是由于地下岩土工程环境的不确定性、深埋管道传热机理的复杂性、钻井难度以及系统初期投资高等因素造成的。如一些已建立的换热模型忽略了岩石和土壤层的分层，因此没有考虑地层导热系数对换热功率的影响。总体而言，国内外对于中深层同轴套管换热器变工况下换热量预测研究较少。为了更好地推广普及中深层地源热泵技术，通过建立中深层同轴套管换热测试试验，采用BP 神经网络算法，对中深层同轴套管换热量进行预测，以期为地源热泵系统的能效和性能提供保障。

1 研究背景

以长沙某改扩建工程能源站新建的一口中深层同轴套管探采测试井为例，进行试验。在不同工况下对其进行换热性能测试（图1）。该地热探采测试井完井深度为2 612 m，终孔孔径为215.9 mm，套管采用177.8 mm管径，中心管下深2 504 m，中心管导热系数为0.21 W/（m·K）。探采测试井采用同轴套管换热技术，建设一套中深层封闭式换热系统，通过闭式循环方式提取地下热量，为地面能源站提供热源。

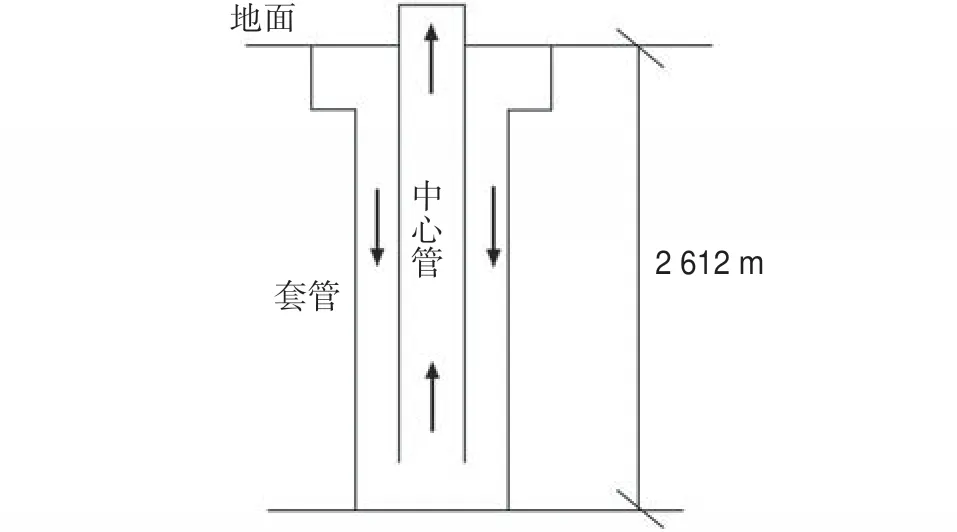
图1 同轴套管地热井示意图Fig.1 Schematic diagram of coaxial casing geothermal well

2 中深层同轴套管地源热泵系统

2.1 热泵系统原理与试验测试

对中深层同轴套管封闭式换热系统冬季供热的运行模式进行测试模拟，将地热井同轴套管与地上系统板换相连接，形成一个封闭式循环水系统，不断提取地下热量。热泵与水箱相连通，热泵制冷产生的低温水进入水箱，水箱内的低温水与板换一次侧高温来水进行换热，依次循环，实现热泵系统冬季供暖运行。中深层同轴套管地源热泵系统试验原理图如图2 所示。

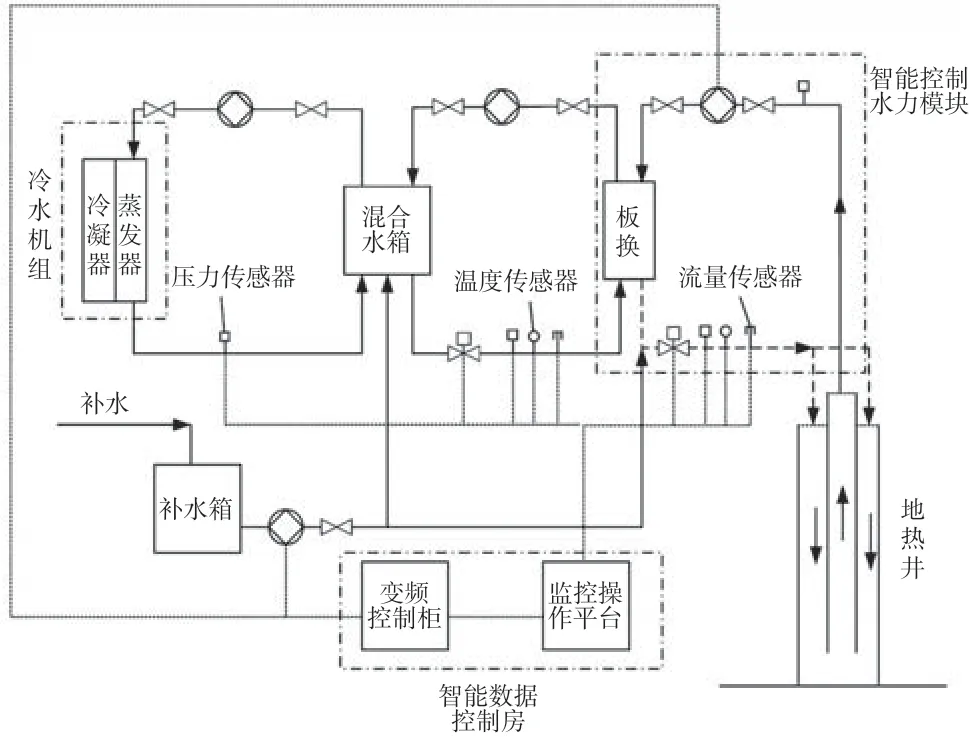
图2 中深层同轴套管地源热泵系统试验原理图Fig.2 Schematic diagram of medium and deep coaxial casing ground source heat pump system

结合开采的地热井进行试验测试，系统主要由冷水机组、混合水箱、智能控制水力模块、补水箱、地热井与智能数据控制房及其他附属设备部件组成，由冷水机组制取冷水，并通过混合水箱和智能控制水力模块按照要求的流量及温度输送至测试井进行循环换热，由智能控制水力模块上的仪表收集数据后传输给监控操作平台，利用智能数据控制房对实时数据进行分析来控制流量和温度在设定参数范围内运行。热泵系统性能测试设备如表1 所列。

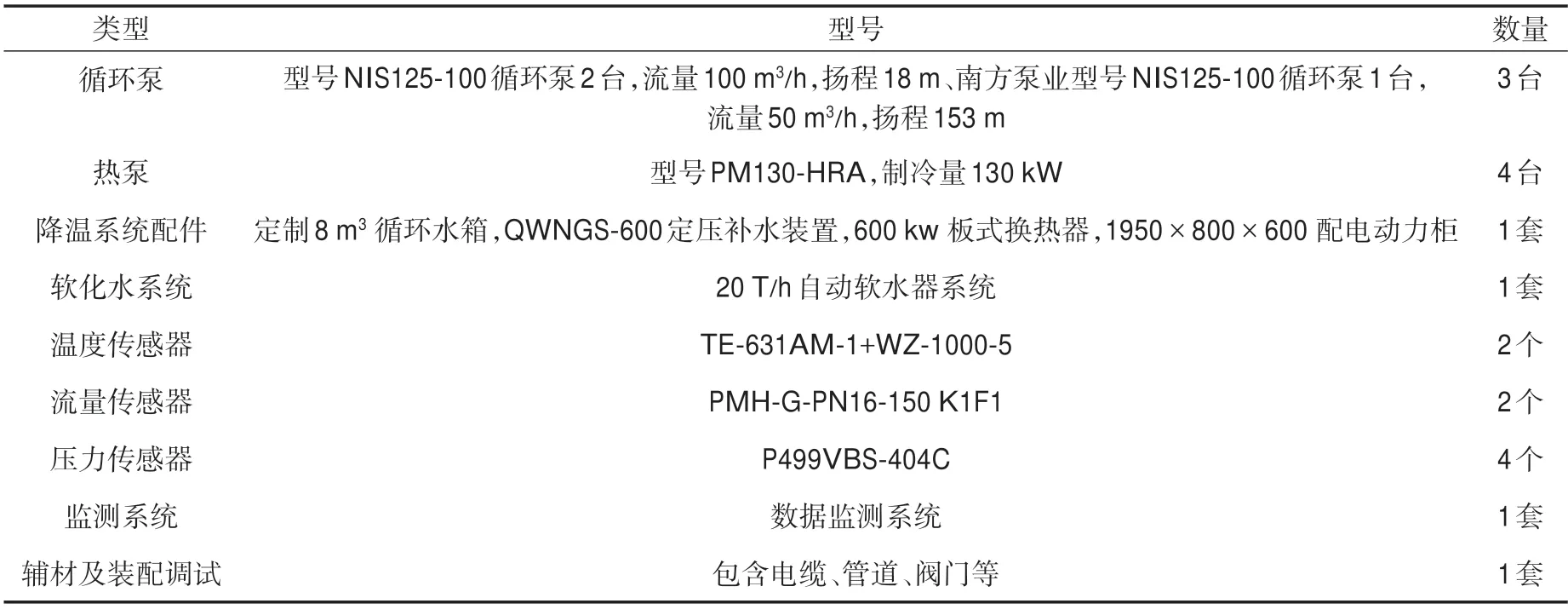
表1 热泵系统性能测试设备Table 1 Performance test equipments of heat pump system

中深层同轴套管系统冬季供热试验测试中，根据单井的运行工况选择不同循环流量，在系统运行过程中，对连续时间内进出测试仪器的温度、流量、热泵的制冷功率、不同井深光纤测试温度进行采集记录，建立BP 神经网络预测模型［17-18］，再进行模拟仿真，从而选择最优的BP 神经网络模型实现测试井换热量的精确预测。

2.2 测试数据分析

BP 神经网络模型需要大量的数据训练学习［19-20］，本次探采结合井测试项目进行3 种不同工况下热交换试验，不同工况循环水流量分别取18 m3/h，23 m3/h，28 m3/h，相应工况地热井回水温度分别控制在15 ℃，12 ℃，10 ℃。每次工况测试连续时间均不少于120 h，每10 min 采集一次数据，不同工况测试间隔时间为15 d，共采集2 333 组数据。通过不同流量、不同回水温度的试验，研究热泵系统中深层同轴套管的换热能力。测试的内容包括：对换热孔循环介质进出口温度、流量等参数进行测试，安装光纤连续观测中心管内不同深度层的温度变化值，根据采集数据来计算不同工况下单井换热量（表2）。各工况运行稳定时，工况三单井换热量最大为563 kW。

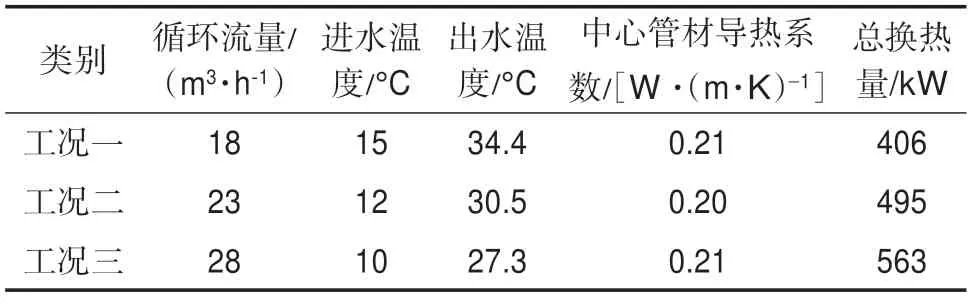
表2 单井试验测试采集数据表Table 2 Test collection data of single well

不同工况换热孔循环介质进出口温度测试情况如图3—5所示。

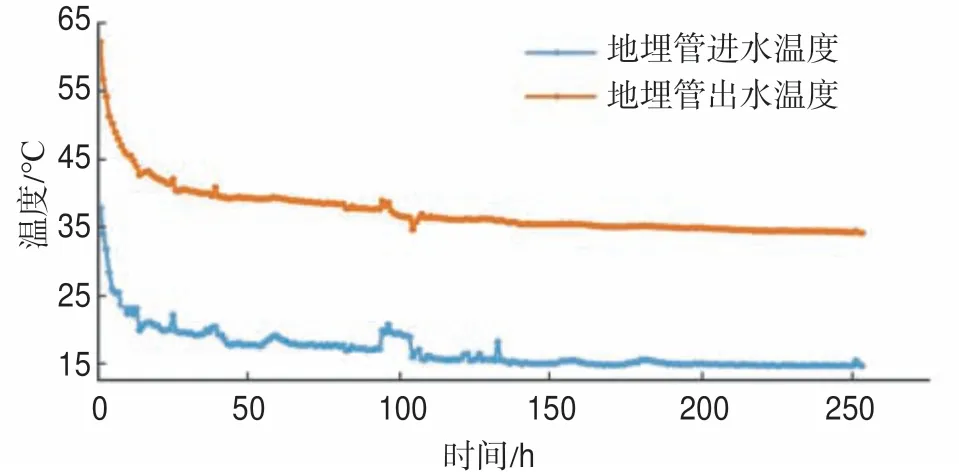
图3 工况一同轴套管进出口温度Fig.3 Inlet and outlet temperature of coaxial casing under No.1 working condition

测试工况一：循环流量为18 m3/h，试验时根据物探测井成果资料进行适度调整，范围控制在17.5～18.5 m3/h。进水温度设定为15 ℃，则出水温度趋于34.4 ℃（图3）。

测试工况二：循环流量为23 m3/h，试验时根据物探测井成果资料进行适度调整，范围控制在22.5～23.5 m3/h。进水温度设定为12 ℃，则出水温度趋于30.5 ℃（图4）。

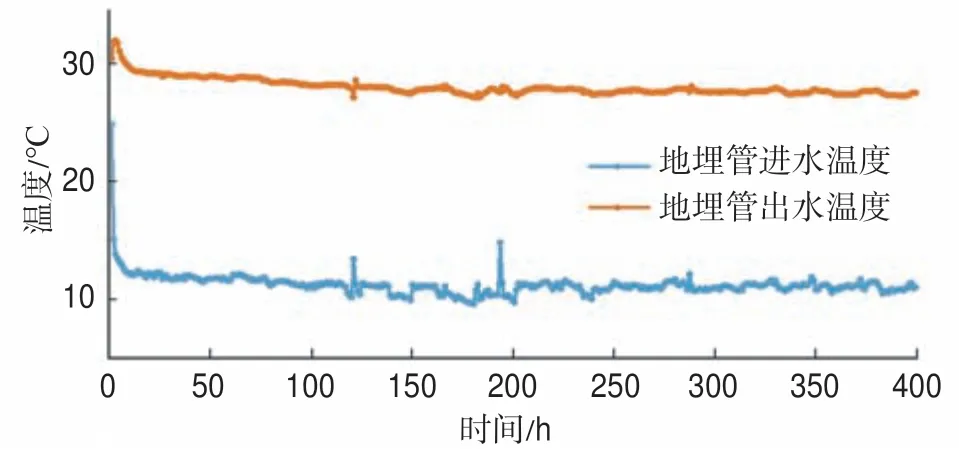
图4 工况二同轴套管进出口温度Fig.4 Inlet and outlet temperature of coaxial casing under No.2 working condition

测试工况三：循环流量为28 m3/h，试验时根据物探测井成果资料进行适度调整，范围控制在27.5～28.5 m3/h。进水温度设定为10 ℃，则出水温度趋于27.3 ℃（图5）。

图5 工况三同轴套管进出口温度Fig.5 Inlet and outlet temperature of coaxial casing under No.3 working condition

3 BP 神经网络预测模型的构建

3.1 BP 神经网络算法结构

BP 神经网络算法结构最基本的模型本质上是一个三层前馈神经网络［21-22］，结构由输入层、隐含层与输出层组成，各层相互之间通过加权系数而紧密相连。根据输入对象与输出对象的复杂程度，需选择合适的神经网络结构进行训练学习，通过加权系数的不断学习优化，实现从输入对象到输出对象之间的非线性映射［23-24］。在进行BP 神经网络结构优化设计、选择时，应该着重考虑2 个方面：①隐含层的数量；②隐含层节点的数量。

在实际应用中根据具体情况来确定隐含层层数，一个神经网络结构中若有一个隐含层，则需要选择合适的隐含层节点数，通过不断的学习训练，使其训练结果不断逼近非线性函数相对应数值，其运算简单，且训练速度快，能很好地实现算法在系统中的精准预测［25］。本次换热量预测时选择单层隐含层，BP 神经网络基本结构如图6 所示。

图6 BP 神经网络基本结构Fig.6 Basic structure of BP neural network

根据BP 神经网络算法的优越性和地源热泵系统运行中同轴套管换热量对系统的影响，提出了一种基于BP 神经网络的同轴套管换热量预测方法。BP 神经网络是基于生物神经元研究而提出的一种抽象化模型，其利用黑盒模型建立起输入层、隐含层与输出层之间的联系，对于复杂非线性对象的预测，BP 神经网络预测算法具有较大的优势［26］。

3.2 BP 神经网络预测模型输入、输出变量的选取

在中深层同轴套管换热量预测模型中，需要对输入变量、输出变量进行合理的筛选，以便更好地实现中深层同轴套管换热系统换热量的精准预测。在BP 神经网络模型建立过程中，输入变量因素考虑得越全面，数据处理得越详细，则预测结果与实际运行结果越接近，BP 神经网络预测模型的精确度就越高［27-28］。如果选择太多的输入变量，会增大模型的运算量，使预测模型训练时间增加，可能造成部分数据不稳定。另外，在项目运行过程中，采集设备会出现一些故障或者缺少相应的采集设备，导致部分数据不能完全采集或缺失，因此，需要通过一些方法对采集上来的数据加以处理、分析，从而建立一个最优的BP 神经网络预测模型。

结合探采井试验采集数据，选取当地风速（x1）、室外温度（x2）、日照时间（x3）、换热孔循环介质循环流量（x4）、回水温度（x5）、前一时刻出水温度（x6）、前一时刻总换热量（x7）、中心管材导热系数（x8）、岩石导热率（x9）、岩石热扩散系数（x10）、岩石比热容（x11）、井深1 950 m 的光纤测试温度（x12）作为神经网络同轴套管换热量预测模型的输入变量，探采井换热量（y1）作为输出变量。输入变量与输出变量之间采用主成分分析法和灰色关联度方法判断各自变量因素与输出变量之间的关联度［29-30］。本次采用灰色关联分析法分析输入变量x1—x12 与输出变量y1 之间的灰色关联度（表3）。在选取输入变量时，考虑与输出变量有关的重要影响因素，依据数据表选取x4，x5，x6，x7，x8，x9，x10，x11 和x12 作为神经网络同轴套管换热量预测模型的输入变量，y1作为输出变量，保证预测模型的精确性。

表3 灰色关联度数据表Table 3 Grey correlation data

3.3 历史数据的预处理

建立BP 神经网络中深层同轴套管换热量预测模型时，模型训练学习需要大量的数据来保证此模型预测的准确性。项目现场采集数据时，可能会因为采集设备出现故障、设备精度不够、采集设备安装不合理、数据传输故障、天气因素、人为因素等造成采集数据的缺失或异常。如果不对这些异常数据进行处理，将大幅降低预测模型的精确度，甚至BP 算法在预测过程中会处于发散状态，预测值远远偏离实际值。因此建立模型时，需要对采集数据进行预处理。

本次将采用偏离率修正方法对采集上来的数据进行2 个方面的预处理：①将采集上来的历史数据按照形式类别进行分类排列；②对数据进行分类排列后，分别计算出各组数据的偏离率，并加以处理。

偏离率计算公式为式中：ε为偏离率；λ为实际值；E为平均值。

各组设定偏离率ε=1，分别对各组数据进行处理。当偏离率小于1 时，认定采集数据合理；当偏离率大于1 时，选择该数据两边相邻时刻数据的平均值作为该数据的修正值［24］。

3.4 输入、输出数据的归一化处理

BP 神经网络中深层同轴套管换热量预测模型建立过程中，由于各输入变量与输出变量之间的关联性不大，如果不对各变量加以处理，会造成预测误差偏大。在上文历史数据修正后，需要对各输入变量与输出变量进行归一化处理，从而保证预测模型的精确度：式中：x为原始采集数据；y为归一化修正后的数据；xmax为原始采集数据中的最大值；xmin为原始采集数据中的最小值。

BP 神经网络同轴套管换热量预测模型建立过程中，采用式（2）将神经网络预测模型中各输入变量与输出变量的数据进行归一化处理，将数据都转化到［-1，1］，然后采用式（3）将经过模型训练后的数据进行反归一化处理，从而实现数据的完整运算。

3.5 BP 神经网络最优预测模型选取

将2 333 组试验数据分为训练集、验证集与测试集三部分，权重分别为70%，27%和3%。BP 神经网络中深层同轴套管换热量预测模型中，设定输入层变量为9，输出层变量为1，学习速率和隐含层节点数量对其预测精确度具有至关重要的作用。若学习速率选择值过大会造成系统运行失调；反之，学习速率选值较小，会影响算法的运行速度，效率下降。本次采用网格搜索法对预测模型的学习速率进行敏感性分析，网格搜索学习率为10-6≤η≤1，选取测试集合{10-6，10-5，10-4，10-3，0.01，0.1}进行训练学习。选取学习速率为0.1 时，模型在训练过程中发生震荡；选取学习速率分别为10-6，10-5，10-4与10-3时，模型在训练过程中不收敛；选取学习速率为0.01 时，训练次数为500 次时效果最好。除此之外，如果隐含层节点个数太少，则BP 神经网络模型所捕捉到的原始数据信息不全，找不到数据之间相关联的规律；反之，隐含层节点数过多，则程序运行时间太长，严重时还会导致过拟合现象，所以选择最优的隐含层节点数量非常重要［31-32］。隐含层节点数由下式确定：

式中：N为隐含层所含节点的数量；a为输入层数量；b为输出层数量；0 ＜m＜10（m=1，2，3，…，9），取

通过MSE（均方误差）指标来选取BP 神经网络同轴套管换热量预测模型合适的m值。均方误差公式为

在BP 神经网络同轴套管换热量预测模型仿真模拟计算中，采用MSE来评价预测模型在隐含层不同节点数量下的精确度。MSE是衡量“平均误差”的重要指标，其数值越小，表明预测模型预测数据精度越高。

根据隐含层节点数量的变化，利用Matlab 软件得到BP 神经网络中深层同轴套管换热量预测模型训练集的均方误差，其具体数值如表4 所列。

表4 在不同隐含层节点数N 取值条件下均方误差Table 4 Mean squared error under different nodes of hidden layers

从表4 可以看出，在m=9（即隐含层节点数N=12）时，训练集模型最大均方误差MSE为0.023%。此时BP 神经网络同轴套管换热量预测模型最优，预测模型结构为9-12-1。

3.6 BP 神经网络最优预测模型验证

选取测试集70 组试验数据样本来验证模型的精确度，依据选取的输入变量和输出变量，采用MATLAB 软件对70 组试验数据样本进行仿真预测，预测结果部分数据如表5 所列。

表5 BP 神经网络测试数据预测值与实际值（部分）Table 5 Predicted and actual values of BP neural network test data

根据表5 结果，得到单井换热量预测数据和实际换热量数据的对比仿真曲线（图7）。对比换热量的预测值与检验值，其平均百分比误差MAPE为0.235%，平均绝对误差MAE为1.261，均方根误差RMSE为1.623，预测准确率为99.765%，误差的主要原因是输入数据的样本量较小，导致模型预测效果不佳。下一步将通过数据增强、集成学习等方式来增加数据量，从而提高模型的预测效果。

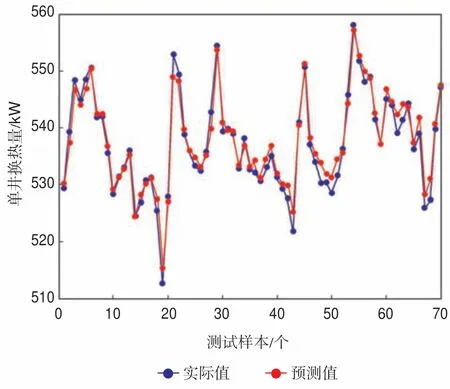
图7 单井换热量预测数据和实际数据对比仿真图Fig.7 Simulation diagram of single well heat transfer prediction data and actual data

BP 神经网络预测模型训练集、验证集和测试集拟合效果均较好，相关系数R分别为0.998 89，0.996 0，0.996 1，综合相关系数R为0.998 04（图8），进一步验证了BP 神经网络中深层同轴套管换热量预测模型的可靠性。

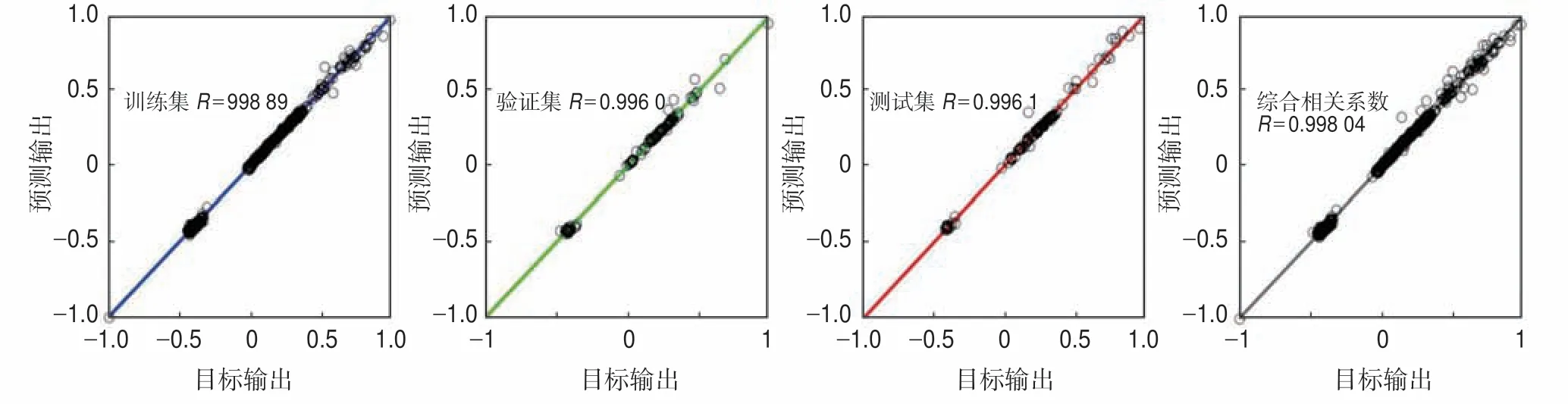
图8 神经网络预测模型预测值和检验值的拟合程度Fig.8 Fitting degree of the predicted and test values of the neural network prediction model

4 结论

（1）对探采井测试项目进行3 种不同工况下热交换试验，系统循环水流量分别取18 m3/h，23 m3/h，28 m3/h，相应地热井回水温度分别控制在15 ℃，12 ℃，10 ℃，根据试验采集数据可知，热泵系统在水流量为28 m3/h，回水温度为10 ℃的工况下稳定运行时，同轴套管换热量最大为563 kW。

（2）结合探采井试验采集数据，选取换热孔循环介质循环流量、回水温度、前一时刻出水温度、前一时刻总换热量、中心管材导热系数、岩石导热率、岩石热扩散系数、岩石比热容、井深1 950 m 光纤测试温度作为神经网络同轴套管换热量预测模型的输入变量，探采井换热量作为输出变量。选取输入变量时，全面考虑与输出变量有关的重要影响因素，保证预测模型的精确性。

（3）BP 神经网络中深层同轴套管换热量预测模型在隐含层节点数为12 时，训练集模型最大均方误差MSE为0.023%，此时BP 神经网络同轴套管换热量预测模型最优，最优预测模型结构为9-12-1。

（4）对比同轴套管换热量预测值与检验值仿真结果，BP 神经网络同轴套管换热量预测平均百分比误差MAPE为0.235%，预测准确率为99.765%，表明BP 神经网络中深层同轴套管换热量预测模型精确性高，可靠性强。