基于动态规整与改进变分自编码器的异常电池在线检测方法
郭铁峰 贺建军 申 帅 王 翔 张彬汉
(中南大学自动化学院 长沙 410083)
1 引言
锂离子电池是一种具有相对质量轻、能量密度高、输出功率高等特点的2次电池。随着全球能源危机愈演愈烈,清洁高效能源供应越来越受到重视,锂离子电池也得到了广泛应用。在锂电池生产过程中,保证同一批次电池具有较好的充放电稳定性是生产环节的重要任务。但由于生产工艺波动,不可避免会出现不符合设计要求的异常电池(如高压差及容量不达标电池等),这些电池如果被用于组成电池组,会影响出厂电池组的预期寿命与安全性能。故为了剔除异常电池,一般在化成工序激活电池后,会设置电池异常检测工序进行异常电池的筛除。该段工序通常会对每个单体电池进行4次充放电实验,并由此确定电池性能的关键参数(如电池容量、搁置压差等)用以判定电池异常情况。
目前,常见的锂电池异常检测方法分为两类,一类是以局部离群因子(Local Outlier Factor,LOF)、聚类算法为代表的基于密度的异常检测方法,如肖健夫等人[1]利用LOF异常算法分析电池充电电压曲线不一致性,实现了对储能电池组的异常检测与故障分类;马速良等人[2]利用一种基于聚类分析架构的遗传优化异常检测新方法实现了对储能电池的个性化异常检测。另一类是基于经典机器学习算法的异常检测方法,如Jin等人[3]提出了结合灰色关联度分析( Grey Relation Analysis, GRA)与孤立森林算法的异常电池数据检测方法;Saxena等人[4]提出了一种利用一类支持向量机模型(One-Class Support Vector Machine, OCSVM)检测电池容量异常衰减趋势的新方法,实现了对电池衰退早期的异常状态检测。
尽管上述已有研究中,多种异常检测方法可以很好地完成储能电池、电力等领域的电池异常检测任务,但上述方法对于电池生产过程的在线异常检测任务而言仍存在一些问题。首先,国内外对电池异常检测的研究多集中在固定电池组的状态检测,但对于生产线上的异常电池检测研究较少。故上述研究提出的模型不适应需要处理大批量电池的在线生产环境。其次,目前业内大部分的电池异常检测方法都是离线检测,即电池无论正常与否都需要先经过完整的充放电流程后,得到判定电池异常的关键参数(如电池容量、搁置压差等)才能进行异常电池的检测。但这意味着极大的能源与时间的浪费,如果可以在首次充电阶段,通过充放电时序数据直接完成大部分电池的异常检测工作,将为电池生产节省大量不必要的能源损耗并提高产线效率。为此一种具有较强数据处理能力的在线异常检测方法亟需提出。
随着近年来深度学习领域的发展,基于深度学习的异常检测技术[5]逐渐成熟,其强大的线性和非线性建模能力可以有效从复杂数据中学习到层次区分特征。在多种深度学习方法中,以变分自编码器[6](Variational Auto-Encoder, VAE)及生成对抗网络[7](Generative Adversarial Network, GAN)为代表的基于生成模型的异常检测方法是当前学术界的研究热点。特别是VAE模型,该类方法可以通过数据重构效果来辨别数据异常。An等人[8]在2015年就证明了其在数据异常检测方面的可行性。其后VAE模型开始在多个领域的异常检测任务中崭露头角,如秦婉亭等人[9]结合滑动窗口与VAE算法实现了对不等长飓风轨迹序列的异常检测;常吉亮等人[10]利用VAE模型实现了对航迹数据的异常轨迹检测,并验证了VAE算法在该方向上的优越性。
综上可见,VAE作为新兴的无监督深度学习方法,在电池异常检测领域有很大的应用潜力,且仍有很大改进空间。首先,传统VAE模型受其网络结构限制,无法很好地处理时序数据。其次,上述研究中,对于VAE模型的分类阈值的选取多是利用网格搜索法或统计的方法进行确定,普适性差且精度较低。针对以上问题,本文在传统VAE网络基础上,结合有较好时序数据特征提取能力的长短时记忆网络(Long Short-Term Memory, LSTM)以及对曲线间形态差异敏感的动态规整算法(Dynamic Time Warping, DTW),从化成工序后的首次充电电压数据着手,设计了一个基于动态规整与改进变分自编码器的锂离子电池异常在线检测方法,即 VAE-LSTM-DTW模型。本模型较传统模型有以下优势:
(1)使用LSTM编解码器优化VAE重构模型,使得模型可以保留时间序列特征的全局相关性,提高模型对时序数据的特征提取与重构能力。
(2)异常度量标准采用DTW,综合考量原始数据与重构数据的单点时刻差异及形态趋势上的相似性,提高了模型对异常数据的检测精度。
(3)将贝叶斯寻优算法与交叉验证方法结合对模型的分类阈值进行选取,在保证结果准确性的前提下,提高了阈值选取的速率与精度。
2 模型与原理
VAE-LSTM-DTW模型如图1,可分为两部分:

图1 锂电池异常检测模型结构图
评价模型如图1(b)。评价模型负责通过DTW算法比对模型对输入数据的重构效果并由此进行异常检测。其中最优阈值λ需要在随机采样、数据均衡的阈值训练集中通过贝叶斯优化进行确定。模型运行时,首先利用DTW算法计算输入数据X与重构数据X′的最短规整距离Ddtw,之后将得到的Ddtw与最优检测阈值λ比较,大于阈值的单体电池判定为异常电池,小于阈值的单体电池判定为正常电池。
2.1 VAE-LSTM重构模型
2.1.1 VAE模型原理
变分自编码器(VAE)[6]是一种基于变分贝叶斯推断与自编码器[11]结构的深度生成模型,模型结构如图2由推断网络与生成网络组成,原理如下:

图2 变分自编码器模型结构图
推断网络可将输入数据X编码为服从某一概率分布的低维隐变量Z。为实现该功能,推断网络需通过关于参数φ的识别模型qφ(Z|X)来进行近似推断关于未知参数θ真实后验概率pθ(Z|X)。通常,该识别模型预设为关于参数φ的普通正态分布。确定识别模型qφ(Z|X) 后,采样输入数据X即可得到隐变量Z。

2.1.2 LSTM改进重构模型
传统VAE模型对时序数据的特征提取与重构能力效果较差[12],为更好完成异常检测任务,本算法引入长短期记忆网络(LSTM)[13]替换传统VAE中的BP层来优化模型对时序数据的特征提取能力,模型如图3。

图3 VAE-LSTM模型结构图
LSTM是一种常用于处理时序数据的改进循环神经网络。LSTM通过状态单元Ct的储存与传递,以及门控单元对历史状态信息Ct-1和候选状态信息C˜t的控制,可以将输入时序数据各时刻长期记忆与单个时刻的短期记忆信息封存在隐藏状态ht中。
为实现对输入数据的特征提取,改进后模型输入数据X经LSTM被映射为一个包含前序时刻特征隐藏状态的张量H=[H1,H2,...,Hn],Hi ∈Rdm。其中单条输入Xi=(a1,a2,...,adt),ai ∈R 将被映射为(dtdm,dt) 时刻对应的dm维隐藏状态特征向量Hi=(hdt-dm,hdt-dm+1,...,hdt),h ∈R,由此实现了对输入数据的序列建模与特征提取。
2.2 DTW评价模型
动态规整算法[14]是一种用于度量两时间序列间相似性的算法,它用一定约束下的动态规划求解两序列匹配累计最小距离,并由此描述相似度,因此对数据重构度量效果更佳。为此,将引入DTW作为重构效果度量标准。图4为某条恒流充电输入数据与其重构数据的DTW最优路径图,其中青色线段显示最优路径。
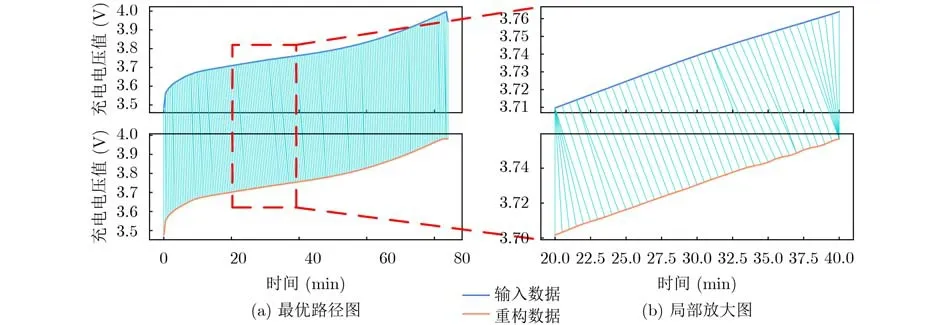
图4 DTW最优路径
Ddtw具体计算过程如下:

(2)设置优化约束条件。DTW算法规定在满足边界条件、连续性约束、单调性约束条件下[14]寻找矩阵Ddt×dt中从起点到终点的最优路径。
(3)迭代寻找最优路径。在优化条件约束的同时,确定输入数据前i个时刻与重构数据Xi′前j个时刻对应的最优路径E(i,j),即最短规整距离Ddtw(ai,bj)
基于式(2)进行迭代寻优,即可得Ddt×dt对应的最优路径与最短规整距离Ddtw(adt,bdt)=E(dt,dt) 。序列间的最短规整距离Ddtw越小,输入数据与重构数据所获得的时间序列相似程度越高。
3 模型训练与数据处理
3.1 数据获取与预处理
本文数据采集于国内一家电池集团股份有限公司的柱状锂电池生产线。企业生产现场见图5,其中图5(a)为老化设备,柱状电池化成激活后,均需通过老化过程使电池性能稳定。图5(b)为电池检测设备,会通过充放电检测电池容量、内阻等参数,并借此实现对电池的分类。

图5 生产现场化成分容设备图
锂电池生产过程中,单体电池化成后需要通过4次充放电检测确定电池质量,检测流程包括:恒流充电、恒流恒压充电、恒流放电、恒流恒压充电、开路电压检测5步,其中单个充放电工序的时长都在80~150 min,且都设定有截止电压、电流。
为降低能源损耗,提高生产效率,文中选择在第1次充电后,利用锂电池恒流充电电压时序数据对异常电池进行在线检测与甄别。故本文选取12 000条人工标注的正常电池充电时序数据作为正例,以及8 000条人工标注的异常电池充电时序数据作为反例,用于构建训练集与测试集。训练集与测试集构建情况如表1。

表1 数据集构建情况表
如图6,受数据采集环境和现场操作影响,原始数据中存在着数据缺失、数据不对齐等问题。故为保证所有采集数据均保留完整的充电信息且各数据点时间权重统一,使用数据前需将数据集通过分段线性插值补齐,并将其截取为图6各点对齐且长度均为170的电池充电前85 min时序数据集。实验平台设置如下,硬件平台使用CPU Intel(R) Core(TM) i7-12700H, GPU GeForce RTX 3060,软件平台选择在Tensorflow 深度学习框架上利用Python语言进行模型搭建。模型输入输出维度均设为170,隐变量维度设为50。
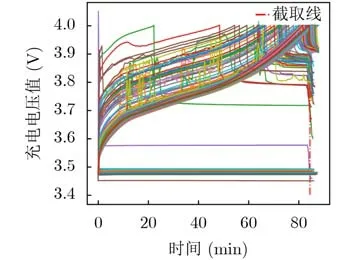
图6 原始数据集曲线图
3.2 模型评价指标
文中各类实验选用准确率(Accuracy)、查准率(Precision)、召回率(Recall)、F1值(F1-score)作为评价指标。其中,准确率是衡量模型检测正常/异常电池能力的指标;查准率是衡量模型对正常电池正确检测能力的指标;召回率是衡量模型对正常样本识别全面性的指标;F1值是查准率与召回率的调和平均数,可以综合反映模型的异常检测性能。
3.3 模型训练
3.3.1 重构模型训练
重构模型利用包含4 000组正常电池数据的重构模型训练集进行模型构建。构建过程中将训练集按4:1划分为训练集与验证集,设定100个训练轮次,整体训练过程中的损失函数变化如图7所示。由图7可知,重构模型损失函数在经过40个训练轮次后开始收敛,最终在60个训练轮次后达到稳定,此时重构模型训练完成。
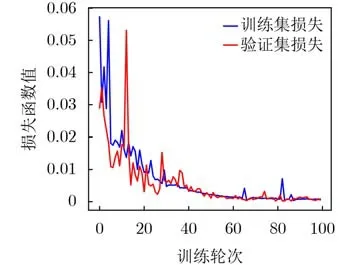
图7 重构模型训练损失函数变化
3.3.2 评价模型最优阈值寻优
在评价模型阈值寻优前,对异常电池曲线进行分析可见,恒流充电过程中的异常充电曲线由其曲线形态与分布可将其分为3类曲线如图8所示。利用重构模型分析其对应Ddtw可知,3类曲线对应分布如图9所示,3类异常电池的Ddtw主要分布在3个区间即[0.2,0.5], [2,20], [40,50],正常电池的分布区间在[0.07,0.3]。
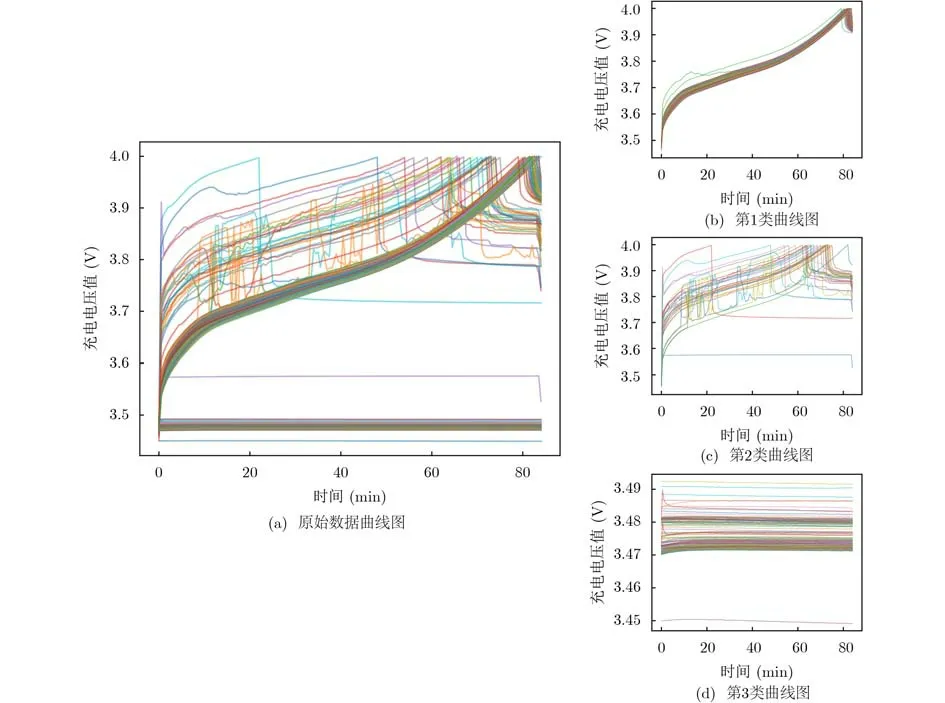
图8 异常电池充电曲线分类图

图9 DTW分布箱线图
统计分析生产过程中产生的异常充电曲线数据可知,异常充电曲线集合中有83%的异常电池曲线分布在Ddtw≤2的范围内,属于第1类异常曲线;3%的异常电池曲线属于第2类异常曲线,13%的电池曲线属于第3类异常电池曲线。第1类异常电池虽然大多存在电池容量偏低的问题,但运行状态较稳定,其异常特征隐藏在曲线中难以简单表征,故其分布与正常电池存在交叠。第2类异常电池曲线虽然也有正常曲线基本可达截止电压,但由于其电化学性能不稳定导致其曲线内波动很大。第3类异常电池曲线不随时间变化,且充电曲线无法达到截止电压,说明电池内部存在微短路,无法正常充放电使用。综上,第2,3类异常电池与正常电池差别明显,仅通过统计学手段即可实现检测,属于简单样本。而第1类异常电池与正常电池分布存在交叠,较难分辨,属于检测问题中的困难样本。为更好解决电池异常问题,下文中将主要针对占比大且难分辨的第1类异常电池数据进行异常检测效果验证实验。
评价模型构建过程借用交叉验证的设计思路与贝叶斯优化算法[15]来确定评价模型最优阈值。训练步骤如图10所示。训练过程中,将阈值训练集分为10组,不重复地抽取一个子集作为验证集,并将其余9组子集数据组合作为训练集进行阈值选择,重复10次。每次训练使用贝叶斯寻优算法在训练集上进行阈值寻优,找到其轮次对应的最优阈值。为保证阈值选取可以同时满足查准率与查全率要求,本文在阈值选择过程中使用F1值作为阈值选择的评价指标。每次阈值选择过程利用贝叶斯寻优以F1值最大为目标进行快速寻优,并将找到的阈值用验证集验证,剔除其中验证集F1值低于80%的阈值后,加权平均可得该批次电池对应的最优异常检测阈值。

图10 阈值寻优流程图
第1类异常电池10折验证分类阈值确定实验结果如表2所示,该实验中训练集与测试集仅含第1类异常电池与正常电池,表中选用训练集的F1值以及测试集的F1值作为评价指标描述最优阈值在阈值训练集与阈值测试集上异常电池分类任务的表现。由表2实验结果可见:通过贝叶斯寻优方法在阈值训练集中寻到的10组最优阈值在各自的阈值测试集中都有较好的表现,其对应的测试集F1值均在0.97以上。故选取10组最优阈值取平均可得第1类异常电池分类阈值λI= 0.216 9。由于后续实验主要针对属于困难样本的第1类异常电池,且第2,3类异常电池的分布区间属于Ddtw>0.2169的子集,故异常检测模型的最优阈值为λ= 0.216 9,即判定Ddtw>0.2169的电池均为异常电池。
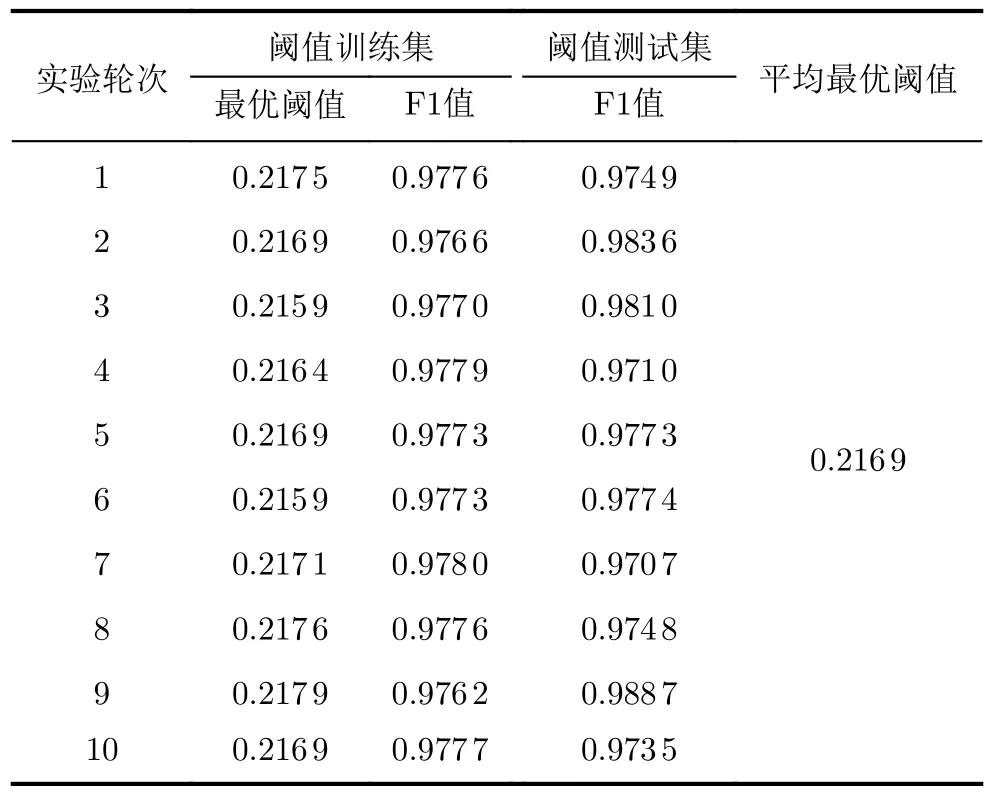
表2 阈值确定10折验证实验结果表
4 实验与验证
4.1 重构效果度量标准对比实验
DTW作为重构效果度量标准,不仅能反映两序列各点间的近似程度,还能反映序列运行趋势上的相似度。由于电池在恒流充电过程中的电压趋势信息也可以间接反映电池性能的稳定性,因此DTW理论上可以满足电池异常检测任务要求。为验证DTW作为重构效果评价标准的有效性与优越性,本文将对比DTW以及Euclidean距离、Frechet距离[16]、Hausdorff距离[17]4类度量标准在电池异常检测任务上的表现。为保证实验不受干扰,对比实验中统一使用3.3.1节训练出的重构模型,阈值均通过3.3.2节方法在评价阈值训练集上选取。对比实验选用只保留第1类异常电池的测试集进行实验验证,评价指标同3.2节。
基于上述4类重构效果度量标准的VAE-LSTM模型异常检测结果如表3所示。其数据分布如图11所示。Euclidean距离、Frechet距离作为评价重构误差的数据分布如图11(a)、图11(b)所示,可见其中蓝色柱状图与橙色柱状图重叠部分很大,这说明两类指标的异常检测分辨率较低,异常检测效果不佳。由表3也易见这两类评价标准的F1值均在0.8以下,且准确率、查准率等指标均在70%左右。故这两类距离难以满足电池数据的异常检测任务要求。

表3 重构效果度量标准对比实验

图11 4类度量标准检测结果分布对比图
Hausdorff距离的表现相对较好。如图11(c)所示,该度量标准下的正常电池与异常电池的柱状分布图通过阈值划分后重叠部分较少,说明两类指标可以将大部分的正常电池与异常电池数据区分开。由表3也易得,这类度量标准的准确率、查准率均达到80%以上,F1值达到0.85以上,异常检测效果较好。DTW异常检测效果如图11(d)所示,可见在DTW度量标准下,模型各项指标均高于另外3类标准,且均较3类标准中表现最好的Hausdorff距离高3%~4%。各项指标均在90%以上,满足锂电池异常检测标准。
综上,实验证明DTW作为重构度量标准较其他常见度量标准更适用于电池时序异常检测。
4.2 与传统异常检测模型效果对比实验
为验证VAE-LSTM-DTW异常检测方法的效果,本文设置了与多种机器学习方法在异常电池检测任务上表现的对比实验。为去除数据集干扰,各个异常检测模型统一使用评价阈值训练集进行训练,测试集与实验指标同4.1节。
实验中选择单类支持向量机(One Class SVM,OCSVM)[18]、离群点检测(Local Outlier Factor,LOF)[19]及孤立森林(Isolation Forest, IForest)[20]3类常用机器学习异常检测方法与VAE-LSTMDTW方法进行比较。由表4易见,前3类算法F1值均在0.75以下,其中表现最好的OCSVM在分类查准率上仅有67.2%,故传统机器学习算法无法满足电池异常检测任务要求。本文提出的异常检测方法在该测试集上对异常电池筛选准确率与查准率均在91%以上,且F1值达到0.93。综上,VAE-LSTM-DTW方法在测试集上有很好的表现效果,比起传统异常检测方法可以更好地完成异常电池检测任务。

表4 机器学习模型异常检测对比实验
4.3 模型改进对异常检测结果影响消融实验
由于VAE-LSTM-DTW对传统VAE从模型结构与重构度量标准两方面进行了改进,为了更好说明模型改进的各部分对异常检测任务的贡献。本节对VAE模型中引入DTW与LSTM带来的异常检测效果上的提升进行了验证。实验中各模型阈值确定同样采用2.3.2节所述方法,实验测试集、评价指标同4.1节,实验效果如表5所示。

表5 模型异常检测消融实验结果
传统VAE模型与VAE-LSTM模型利用MSE做重构度量标准,其筛选结果如图12(a)、图12(b)所示。可见两模型正常曲线与异常曲线分布重叠都很深,异常检测分类效果较差。虽然VAE模型运行速度很快,但其异常检测准确率仅有68.9%,不能满足异常检测要求。VAE-LSTM虽然运行时间有所增加,但较VAE的查准率与准确率增加4%左右,可见引入LSTM可有效改进模型的时序异常检测效果。但两类模型各项指标均低于80%,可见仅通过MSE无法满足电池异常检测要求。
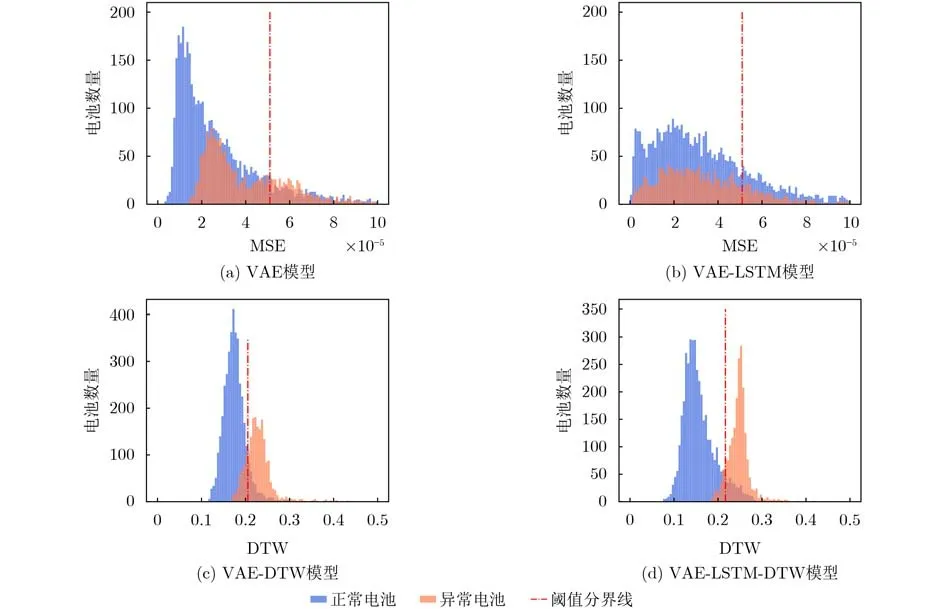
图12 消融实验异常检测结果分布对比图
利用DTW改进重构评价标准的VAE-DTW模型如图12(c)所示,在异常检测效果上效果有很大的提升,其查准率、召回率等指标均达到90%以上,综合指标F1值达到0.91。对比传统VAE模型,说明使用DTW作为重构度量标准可以更全面地反映正常、异常电池间的特征差异,虽然单体电池检测时长由于计算最优路径有所增加,但仍控制在0.075 s,可较快完成在线检测任务。
VAE-LSTM-DTW模型异常检测效果如图12(d)。可见在继承了上述模型的检测效果基础上,VAELSTM-DTW模型更进一步减小了正常数据与异常数据分布的方差,提高了模型的分辨率。该模型各类指标均比VAE-DTW模型有1%~3%的提升,且运行时间仅增加了0.009 s,可以很好完成异常检测任务。可见LSTM与DTW的结合改进,可以明显提高模型对时序数据的特征提取能力。
综上,本文提出的VAE-LSTM-DTW模型对异常数据检测处理的各类指标上均有较优表现,较原始模型有所改进,且模型各部分组成均可以达到加强模型特征提取能力、提高模型异常检测能力的效果。
5 结束语
本文提出一种基于动态规整与改进变分自编码器的锂离子电池异常在线检测方法。首先,利用LSTM层替换了传统VAE中的BP神经网络,改进了VAE模型对时序数据的处理能力。其次,使用DTW作为异常检测的度量标准,并通过贝叶斯寻优算法与交叉验证相结合的方法对DTW的分类阈值进行最优值选取,提高了异常检测精度与效率。通过3组对比消融实验说明,使用LSTM作为编码器和解码器,可以兼顾时序数据的全局相关性;使用DTW作为重构效果评价标准,可以更好地放大异常曲线与正常曲线间的差异,提高异常检测效果;模型各项指标均高于对比的其他异常检测算法,可满足锂离子电池异常在线检测任务要求,为企业的异常电池预筛选提供了可行方案,具有一定的科研与实用价值。

