端接复杂电路传输线网络的电磁耦合时域并行计算方法

叶志红 张 玉 鲁唱唱

①(重庆邮电大学通信与信息工程学院 重庆 400065)

②(电网环境保护全国重点实验室 武汉 430074)

1 引言

传输线是电子电气设备信号传输的载体，尤其是设备集成度愈来愈高，多类功能的电路模块布局在同一封闭空间，使用传输线互联构成复杂的传输线网络结构。传输线端接设备电路多为线性元件和二极管、三极管等非线性元件组成的复杂电路，空间电磁场通过传输线耦合产生的干扰信号作用到这些敏感元器件上将造成潜在性失效甚至永久性损伤。因此，开展空间电磁场作用端接复杂电路传输线网络的电磁耦合计算方法研究，有助于电子电气设备开展电磁防护设计。

传输线网络的电磁耦合过程涉及空间强干扰源的电磁辐射、传输线电磁耦合与复杂电路传导干扰并存的场路混合问题。针对此类场路混合问题，国内外学者已经开展了大量的研究。文献[1–5]研究了频域和时域Baum-Liu-Tesche(BLT)方程方法，应用于传输线网络的电磁耦合计算。但是，频域BLT方程仅能对端接线性时不变负载的传输线网络进行电磁耦合分析，而且每次计算只能获得单个频点的干扰响应。时域BLT方程虽然可以处理宽频带干扰源作用传输线网络的电磁耦合问题，但是涉及大量卷积运算，计算过程较为繁杂。另外，部分学者将时域有限差分(Finite Difference Time Domain,FDTD)方法与仿真电路模拟器(Simulation Program with Integrated Circuit Emphasis, SPICE)

处理非线性直流和非线性瞬态等电路仿真分析的优势相结合，提出了多类高效的时域混合算法。其中，一些学者使用FDTD计算传输线周围空间电磁场，基于此推导了多导线、同轴线等多类线缆的SPICE等效电路，并通过SPICE软件建模仿真得到各类线缆端接电路瞬态干扰响应[6–8]。但是，该方法在构建各类线缆的SPICE等效电路时，推导过程较为复杂，而且空间电磁场与线缆瞬态响应需要分开计算。一些学者将端接复杂电路的传输线网络分解成传输线和电路两个子系统，在每个时间步进上，利用细导线FDTD提取传输线作用复杂电路的电流源与等效电容的并联电路，并使用SPICE软件求解电路端口电压用于修正对应FDTD网格上的电场，达到空间电磁场与电路瞬态干扰响应同步完成计算的目的[9–11]。这类方法虽然使用细导线FDTD实现了传输线耦合的快速计算，但是，当传输线为多导线等复杂类型线缆时，细导线FDTD不再适用。

除此之外，部分学者结合FDTD方法与改进节点分析法(Modified Nodal Analysis, MNA)，提出了一种时频混合算法[12,13]。文献[12]分别采用高阶FDTD(2,4)与MNA方法计算了传输线与端接电路的瞬态响应，实现了复杂传输线网络串扰问题的快速仿真分析。文献[13]研究了微带整流电路的电磁耦合计算方法，首先使用FDTD全波仿真整流电路端口的等效电压源，然后利用传输线方程结合1维FDTD求解微带线的电磁耦合响应，最后通过MNA完成端接电路的传导干扰仿真。然而，MNA需要根据电路元件参数构建相应关系矩阵，端接电路元件数量越多，关系矩阵的建立难度越大。

课题组前期基于传输线方程，并与NGSPICE软件和FDTD方法相结合，开展了相应时域混合算法的研究，实现了传输线端接复杂电路的电磁耦合快速计算[14]。该算法首先通过匹配负载替换传输线端接复杂电路，然后对多导体传输线的电磁耦合通过传输线方程进行建模，并通过FDTD求解得到匹配负载端口的入射电流响应。在每个时间步进上，将此入射电流馈入复杂电路进行激励，并对复杂电路使用NGSPICE软件进行建模和传导干扰分析，实现场路协同仿真。但是，该方法忽略了干扰信号在电路端口的反射以及传输线网络端接电路之间的相互影响。

因此，基于FDTD方法、传输线方程和NGSPICE软件，结合诺顿定理和置换定理，并引入消息传递接口(Message Passing Interface, MPI)并行技术，研究一种高效的时域混合并行算法(FDTD-Transmission Line equation-NGSPICE, FDTDTL-NGSPICE)，有效解决传输线网络与复杂电路一体化的场线路联合协同仿真难题。

2 时域混合并行算法理论

图1为典型的端接复杂电路的传输线网络场路混合模型，多根传输线平行放置在理想导电板上，各端口接有电容、电感等集总元件以及二极管、晶体管等非线性元件组成的复杂电路，空间干扰源以任意角度辐射作用到传输线网络。

图1 端接复杂电路传输线网络的场路混合模型

如图2所示，时域混合并行算法实现端接复杂电路传输线网络的电磁耦合快速计算包括4个重要步骤：(1) 对移除传输线网络之后的理想导电板或屏蔽腔结构进行物理建模，采用FDTD并行算法结合立体光刻模型(STereoLithography, STL)网格剖分技术，模拟得到理想导电板上或屏蔽腔内部的空间电磁场分布，并在每个时间步进上，提取当前时刻的传输线切向和垂直方向电场分量，引入传输线方程作为等效分布源项；(2) 构建传输线网络的等效电路，根据诺顿定理，将传输线对端接电路的作用通过诺顿电路等效形成电路子系统，应用置换定理，将复杂电路置换为受控电压源并馈入传输线组成传输线子系统；(3) 通过传输线方程对传输线子系统的电磁耦合过程进行建模，使用FDTD并行算法迭代求解得到传输线沿线各点的瞬态电压和电流响应，获取对应诺顿电路的电流源和等效导纳，并在每个时间步进上引入复杂电路子系统作为激励源；(4) 构建各个电路子系统的网表文件，并与FDTD计算空间电磁场保持同步，实时更新网表文件中的诺顿电路电流源项的参数值，使用NGSPICE软件读取网表文件进行仿真，提取复杂电路端口电压反馈给传输线子系统获得受控电压源大小，将干扰信号在电路端口的反射引入传输线子系统，以此实现干扰信号在传输线网络端接电路之间的来回传输。

图2 时域混合并行算法的实现流程

为了详细介绍时域混合并行算法的实现过程，下面将从传输线网络等效电路模型构建和电路子系统传导干扰分析两方面进行阐述。

2.1 传输线网络的等效电路模型

通常情况下，电子设备中的多导体传输线需要贴近接地板或屏蔽腔体壁布线。根据镜像原理可知，多导线上的电流与其镜像电流等幅反相，多导线的综合辐射效应较弱，可以被忽略。此时，使用时域传输线方程对多导体传输线的电磁耦合进行建模，可以避免对精细多导线的直接网格剖分。具体的时域传输线方程表达式为

式(3)和式(4)中的ET(y,t)和EL(y,t)由空间电磁场计算得到，具体计算公式见文献[15]。需要说明的是，等效分布源项所需空间电磁场与多导线散射场无关。为此，在FDTD模拟空间电磁场分布时，需要将多导线移除。

使用FDTDTL算法[15]对传输线方程(式(1)和式(2))进行求解，处理方法是对传输线方程中的时间和空间偏微分项通过FDTD的中心差分格式进行离散，随着时间步进迭代求解得到多导线沿线各点的电压和电流响应。具体的多导线电压电流迭代公式见文献[15]。

当计算区域较大或者干扰源频率较高时，FDTD计算所需空间步长必须划分较细，导致网格量增多而大幅降低空间电磁场的求解效率。因此，为了提高多导线电磁耦合的仿真效率，将MPI并行技术引入FDTDTL算法，同步并行计算空间电磁场与多导线沿线各点的瞬态电压和电流响应。具体实施方法是将电压和电流节点设置在FDTD网格的棱边和中心处，与电场和磁场的位置重合。然后将整个计算区域分解成多个相对独立的子区域，并分配给不同的线程执行运算，线程之间的数据通信通过MPI库函数实现，如图3所示。具体的FDTDTL并行算法执行过程见文献[16]。

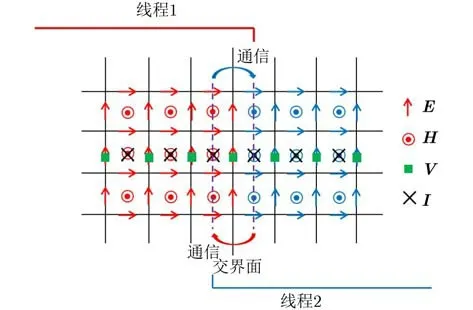
图3 FDTDTL并行算法不同线程之间的数据通信

如图4所示，多导线两端复杂电路的端口电压在进行FDTD中心差分离散时缺少重要的电流信息，必须采用前向差分和后向差分进行处理。

图4 复杂电路端口电压的前向和后向差分格式

由式(6)可知，多导线对端接电路的作用可以通过电流源ISH和等效导纳Geq并联构成的诺顿电路进行等效。同理，对多导线终端电路端口电压VN采用后向差分进行处理，获得多导线作用终端电路的诺顿等效电路，由电流源ILH和等效导纳Geq构成。这里的Geq由式(7)计算得到，ILH的计算公式为

为此，将多导线对两端端接电路的激励等效为诺顿电路，并与对应复杂电路构成电路子系统，而复杂电路等效为受控电压源加载到多导线端口，构成传输线子系统，最终得到传输线网络的等效电路模型如图5所示。传输线子系统的电磁耦合，通过FDTDTL并行算法即可求解得到传输线沿线各点电压和电流响应，进而使用式(8)和式(9)计算得到诺顿电路的电流源大小。

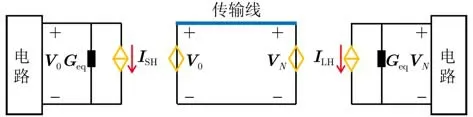
图5 端接复杂电路传输线网络的等效电路模型

2.2 复杂电路的传导干扰分析

为了分析电路子系统的传导干扰，使用电路软件NGSPICE进行仿真。

这里以终端电路子系统为例，如图6所示，说明NGSPICE软件传导干扰仿真的具体实施步骤，包括：

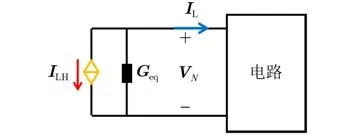
图6 终端电路子系统的传导干扰分析模型

图7 端接复杂线性电路传输线网络的电磁耦合模型

(1) 构建终端电路子系统的网表文件，保存为cir格式；

(2) 根据多导线上新时刻的电流，使用式(9)计算诺顿电路的电流源项，并实时更新cir文件中的电流源数据；

(3) 使用NGSPICE软件读取电路子系统的cir文件，使用瞬态仿真求解器计算复杂电路各元件上新时刻的电压和电流，提取电路端口新时刻的电压反馈给传输线子系统，获得传输线子系统新时刻的终端受控电压源值。

在求解传输线子系统电压和电流响应的每个时间步进上，按照上述过程同步执行始端和终端电路子系统的传导干扰分析，即可实现空间电磁场辐射、传输线耦合与电路传导干扰并存的场线路联合协同仿真。

3 数值模拟

采用时域混合并行算法与电磁仿真软件CST CS，对平面波辐照理想导电板上以及屏蔽腔内端接复杂电路传输线网络的电磁耦合进行数值模拟及仿真结果对比，验证所提算法的正确性和高效性。运行两种方法的硬件环境为联想服务器(64G内存，Intel Xeon Silver 4210R CPU@2.4 GHz 2.39 GHz)，而且时域混合并行算法使用16线程执行并行计算。

图8为时域混合并行算法和CST CS模拟得到的6号电路端口以及节点2的电压响应，可以看出，两者在幅值和变化趋势上基本保持一致。同时，时域混合并行算法与CST CS计算该算例所耗用的时间分别为16 s和58 s，说明时域混合并行算法在保持与CST CS相同仿真精度的同时，计算速度得到了明显提升，16线程的计算效率提高了约3.6倍。

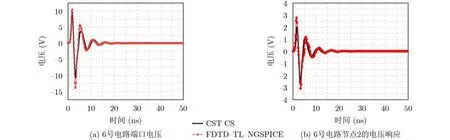
图8 算例1的传输线网络端接电路电压响应

算例2 端接复杂非线性电路的传输线网络电磁耦合模型如图9所示，接地板与传输线的结构参数以及均与算例1的相同。多导线端口1～5均接有集总元件组成的线性电路，端口6接有集总元件以及二极管组成的复杂非线性电路。各电路中的电阻、电感以及电容的参数值见表2，二极管的型号为1N4376[14]，模型参数为饱和电流IS=8.758 9×10-10A、 发射系数N=1.888 11、 内阻RS=2.535 77 Ω、零偏置结电容CJO=1 pF 和结电压VJ=0.75 V。入射波同样为高斯脉冲，波形参数与算例1的相同。

表1 复杂线性电路的元件参数表

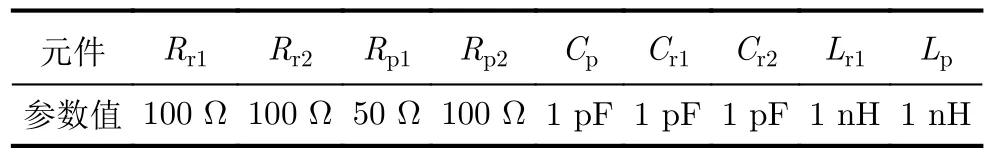
表2 复杂非线性电路的元件参数表

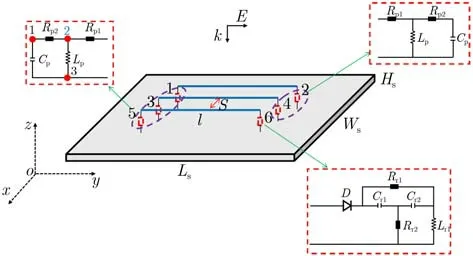
图9 端接非线性电路传输线网络的电磁耦合模型

时域混合并行算法与CST CS计算该算例所需时间分别为21 s和77 s，两种方法模拟得到的6号电路端口和5号电路节点2的瞬态电压响应如图10所示。可以看到，时域混合并行算法模拟端接复杂非线性电路传输线网络的电磁耦合问题，仍能保持很高的计算精度和计算效率。

图10 算例2的传输线网络端接电路电压响应

算例3 将算例2使用的传输线网络模型放置于屏蔽腔内，如图11所示，验证时域混合并行算法用于复杂电磁环境下端接复杂电路的传输线网络电磁耦合模拟的正确性。屏蔽腔的长宽高分别为Lc=0.6 m,Wc=0.5 m, Hc=0.5 m，腔体顶部开有3条矩形缝，缝隙的长度和宽度分别为l=40 cm和w=4 cm，相邻缝隙的间距S为2 cm。外部平面波源设置与上述算例相同。

图11 屏蔽腔内传输线网络的电磁耦合模型

同样地，图12给出了时域混合并行算法与CST CS模拟得到的6号电路端口和5号电路节点2的电压响应，可以看到，两者在幅度和变化趋势上仍能保持很好的一致性。时域混合并行算法与CST CS计算该算例所需时间分别为55 s和246 s，在计算区域扩大以后，时域混合并行算法的计算效率提升更为明显。

图12 算例3的传输线网络端接电路电压响应

4 结束语

本文基于FDTD、传输线方程以及诺顿定理与置换定理，结合NGSPICE软件，并引入并行技术，研究了一种高效的时域混合并行算法，实现多导线与端接复杂电路一体的传输线网络电磁耦合快速计算。本该算法应用诺顿定理和置换定理，构建传输线网络的等效电路，使用FDTDTL并行算法同步快速计算空间电磁场与传输线上瞬态干扰响应，避免对传输线精细结构的直接网格剖分建模，并借助NGSPICE软件在复杂电路快速仿真方面的优势，实现对传输线端接复杂电路的传导干扰分析。相较于其它场路混合算法，所提时域混合并行算法有效解决了空间电磁场辐射、传输线耦合与电路传导干扰并存的场线路联合协同时域仿真难题。