基于硬件损伤的认知反向散射通信网络鲁棒安全资源分配算法

徐勇军 姜思巧 张海波 王正强 周继华

①(重庆邮电大学通信与信息工程学院 重庆 400065)

②(移动通信技术重庆市重点实验室 重庆 400065)

③(航天新通科技有限公司 重庆 401332)

1 引言

随着未来物联网(Internet of Things, IoT)系统中传感器节点数量的快速增长，对能量供给和频谱资源的需求也在迅速增加[1]。为了解决低功耗IoT电池容量受限与网络运行寿命低的问题，基于无线射频供电的反向散射通信应运而生[2]。反向散射的主要特点是：利用现有周围的无线电射频信号进行无线供能，并且在射频源信号上调制自己的信号，以此来实现低功耗反向散射通信与无线供能[3,4]。但随着IoT节点数量的快速增长，反向散射通信网络频谱短缺问题日益严峻。针对该问题，将认知无线电引入到反向散射通信技术中，形成一种新型的认知反向散射通信模式，可以有效提高系统的频谱效率[5]。

基于认知反向散射网络频谱效率提升与能耗降低双重优势这一特点，大量学者已经从物理层安全[6,7]、性能分析[8,9]和资源分配[10-16]等方面进行研究。例如，文献[10]对带内全双工认知反向散射通信网络吞吐量最大化资源分配问题进行了研究，通过设计时间分配和能量收集时间因子来提高系统的传输效率。但只考虑了单一主用户场景，过于理想，且忽略了用户服务质量(Quality of Service,QoS)约束，无法保障用户最低传输速率的要求。针对相同的网络传输模型，考虑主系统的最大发射功率和最小速率的约束，文献[11]研究了次用户和吞吐量最大化问题。文献[12]提出了一种新的先收集-再传输和反向散射混合模式，以最优的时间调度来实现次级系统吞吐量最大化。但只考虑了一个主接收机(Primary Receiver, PR)，且忽略了反射系数的设计。文献[13]通过共同优化次级系统的反射系数和发射功率来实现单个反射节点容量最大化。与单节点不同[13]，文献[14]研究了多次级节点吞吐量最大化问题，优化了主动传输和反向散射模式之间的时间分配系数。然而，上述工作都是在完美频谱感知结果下完成的。事实上，在实际的认知无线通信场景中，由于环境中噪声的影响，很难获得完美的频谱感知结果。文献[15]考虑了频谱感知误差的影响，通过联合优化检测阈值、能量收集时间和传输时间因子，来最大化次级系统的能效。然而，文献[15]并没有考虑通信链路传输安全性。由于无线信道的广播特殊性，通信的隐私和安全性显得尤为重要。针对反向散射通信系统安全传输问题，基于完美信道状态信息(Channel State Information,CSI)，文献[16,17]分别从用户窃听与人工噪声的角度研究了基于安全通信的资源分配算法。事实上，由于实际系统中存在量化误差、信道估计误差等不确定性因素，因此想要获得完美CSI几乎不可能，从而导致这类算法会有较大的性能损失，如较高的中断概率。文献[18]考虑了一个多标签反向散射通信网络，在不完美CSI下，通过优化反射时间、人工噪声功率比和反射系数，提出了一个基于能效的最大最小公平资源分配问题。

综上可知，现有工作都集中在完美频谱感知、完美CSI、无信息泄露等理想假设下完成的，忽略了频谱感知误检概率、信道不确定性、用户窃听等实际因素的不良影响。同时，假设所有节点或收发机都工作在稳定的理想工作状态(即完美硬件条件)也是不切实际的。在实际认知反向散射通信系统中，设备制造商使用低成本的硬件组件来降低部署成本(如配备低成本射频收发器、模数转换器)可能会导致系统遭受严重的硬件损伤(如同相/正交相位不平衡、相位噪声和放大器非线性)[19]，这些硬件损伤可能会导致系统性能进一步下降。

为了提高认知反向散射通信系统抗硬件损伤能力，克服信道不确定性和频谱感知误差的影响，并保障系统的安全性，本文提出了一种更贴合实际应用需求的鲁棒安全资源分配算法，主要贡献如下：

(1)构建了一个考虑硬件损伤和含有窃听用户的认知反向散射通信安全传输模型。考虑了每个认知反向散射用户(Cognitive Backscatter User, CBU)的最小安全速率、传输时间、能量收集和反射系数等约束，建立了CBU吞吐量最大化的资源分配问题，该问题是一个混合整数非线性分式规划问题，很难直接求解。

(2)为了提高系统的鲁棒性，在原模型中引入信道估计误差和频谱感知误差，以获得其对应的无限维鲁棒资源分配问题，然后利用连续凸近似和最坏准则方法将其转化成确定性的凸优化问题，并设计了一种基于迭代的鲁棒吞吐量最大化算法。

(3)仿真结果表明，与传统非鲁棒算法对比，所提算法具有较好的收敛性和鲁棒性。

符号定义：E{x}表示期望运算，CN(µ,σ2)表示一个均值为µ和 方差为σ2的复高斯分布，max(x,0)表示取x和0中较大的数， |x| 表示x的绝对值，Pr{X|Y}表示在事件Y条件下事件X发生的概率。

2 系统模型及问题描述

考虑一个多CBU的反向散射通信网络，系统模型如图1所示。网络中存在1个主基站、M个PR、K个CBU、1个认知信息接收机(Cognitive Information Receiver, CIR)和1个窃听者，且用户集合定义为∀k ∈K={1,2,...,K},∀m ∈M={1,2,...,M}。假设设备收发端均配备单天线，每个

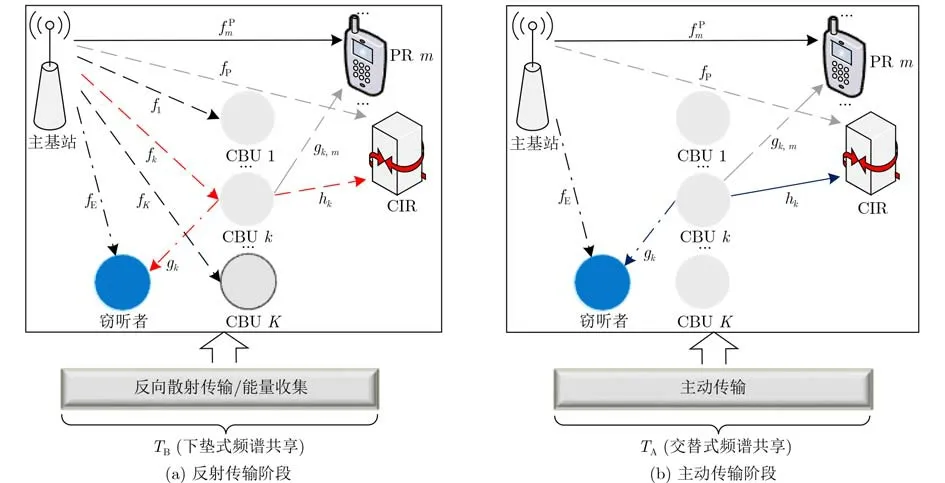
图1 认知反向散射通信网络

在反射传输阶段PR占用授权频谱，CBU进行反向散射时会对PR造成干扰，但在主动传输阶段，PR未占用授权频谱，因此不会对PR产生干扰。基于干扰温度模型[5]，第k个CBU对第m个PR产生的干扰功率需满足如式(14)的约束

综上所述，基于完美CSI的认知反向散射通信网络吞吐量最大化资源分配问题可以表示为

3 鲁棒安全资源分配算法设计

3.1 含频谱感知误差的鲁棒安全问题描述与转换

在实际的认知反向散射通信网络中，由于存在频谱感知误差，CBU无法完全准确地判断授权频谱是否被PR占用。这种误差会导致CBU的传输效率变低、对PR的干扰功率增加，并且会造成不必要的能量消耗。定义qfa和qmd为CBU的虚警概率和误检概率，qo为PR占用授权频谱的概率。基于贝叶斯条件概率公式，有如表1所示的频谱检测情况[21]。

表1 频谱检测情况

考虑频谱感知误差的影响，CBU的有效吞吐量重新表示为

在实际的认知反向散射通信网络中，窃听者在网络中的位置是随机的，与主基站没有任何合作，从而使得相关CSI无法准确估计，因此考虑如式(21)的有界窃听信道不确定性模型

其中，RG和RE表 示信道不确定性集，gˆk和fˆE分别表示信道估计增益，∆gk和 ∆fE表示信道估计误差，δkG和δE表示对应的信道估计误差上界。结合式(17)—式(21)，P1可以描述为如下鲁棒资源分配模型

C8表示不确定性参数集合。问题式(22)是一个含参数摄动的非凸优化，难以直接求解。基于此，针对 C¯1中的不确定性，则有

虽然P3是一个确定性优化问题，但优化变量的耦合关系仍然使得上述问题无法求解。

3.2 非凸优化问题转换

为了处理 Cˆ1的非凸性，引入辅助变量

由于式(30a)和式(31a)，问题仍是非凸的。采用连续凸近似方法和泰勒级数展开[19]，式(30a)和式(31a)近似为

可以看出，P4-1和P4-2都是凸问题，可直接采用凸优化求解工具进行求解，且提出如算法1所示的基于迭代的鲁棒资源分配算法和如图2所示的算法求解流程图。

图2 算法求解流程图

3.3 收敛性分析

根据式(40)和式(41)，可以得到

式(42)说明P4的目标值在每次迭代后均不下降。由于系统总吞吐量是有上限的，因此提出的算法1收敛。

4 仿真分析

算法1 基于迭代的鲁棒资源分配算法

图3描述了算法的收敛性能图。从图3可知，本文提出的算法经过大概5次迭代就趋于收敛了，具备良好的收敛性；当Ikm,amx增加时，系统的吞吐量也会相应增加。这是因为增加Ikm,amx可以容忍更高的干扰功率，从而使得CBU的反射系数和发射功率增大，进而提高系统的吞吐量。

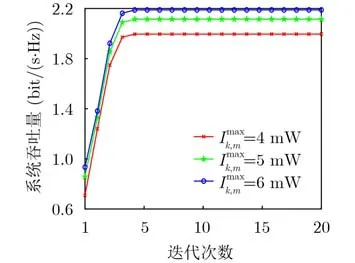
图3 算法收敛分析图

图4描述了系统保密吞吐量与δE的关系。从图4可以看出，随着δE的增大，系统的保密吞吐量会减小；而随着δkG的增大，系统的保密吞吐量会增大。其原因是δE的增加会导致窃听者的信干噪比增大，从而增加窃听者的吞吐量，进而导致系统的保密吞吐量减小。此外，当δkG增大时，窃听者的信道环境会变差，使得窃听者的吞吐量减少，从而使得系统的保密吞吐量增大。

图4 系统保密吞吐量与 δE的关系

图5 系统吞吐量与 P0的关系

图6 系统保密吞吐量与 r 的关系

图7 不同算法与 I的关系

图8描述了保密中断概率与不同算法的关系。从图8可看出，当δE较小时，本文算法的保密中断概率接近于0。因为本文算法消耗了较多的自由度，来保证较强的鲁棒性。然而，其他算法产生了明显更高的保密中断概率。对于无硬件损伤鲁棒算法，硬件损伤会产生干扰，使得CBU的传输速率恶化；采用完美频谱感知鲁棒算法，频谱感知误差会产生干扰，使得CBU的传输速率恶化；采用非鲁棒算法忽略了信道的不确定性，因此无法满足CBU的保密速率，尤其是对于较大的不确定性参数δE来说。本文算法的平均保密中断概率比非鲁棒算法降低了8.73%，这些结果进一步验证了所提算法的鲁棒性。

图8 信道不确定性对中断概率的影响

5 结束语

本文研究了认知反向散射通信系统下的鲁棒安全资源分配问题。考虑了每个CBU的QoS和能量约束，基于有界信道不确定性和频谱感知误差模型，建立了吞吐量最大化的非凸鲁棒安全资源分配问题。利用最坏准则、连续凸近似和交替优化，通过凸优化工具来求解该问题。仿真结果表明，所提算法的平均保密中断概率比非鲁棒算法降低了8.73%，且具有较好收敛性。